基于薄板理论的偏航轴承接触载荷分析*
毛范海,范峻凯,董惠敏,王德伦
(大连理工大学 机械工程学院,辽宁 大连 116024)
基于薄板理论的偏航轴承接触载荷分析*
毛范海,范峻凯,董惠敏,王德伦
(大连理工大学 机械工程学院,辽宁 大连 116024)
文章基于薄板理论与赫兹接触理论,提出了一种考虑轴承套圈轴向柔性变形的偏航轴承接触载荷计算方法,该计算方法的计算结果与有限元仿真结果较为接近。利用该方法分析了轴承套圈厚度及螺栓分布圆直径对偏航轴承的接触载荷的影响。研究成果为偏航轴承的结构优化设计提供了理论依据。
偏航轴承;柔性变形;接触载荷;薄板理论
0 前言
偏航轴承作为风力发电机组的关键支撑结构,对风机的质量起着非常重要的作用。相较于普通轴承,偏航轴承具有大直径、大载荷、小刚度的特点,研究适用于大型偏航轴承的计算方法、分析方法具有重要的意义。
Zupan、Prebil[1]假设轴承套圈为刚性,弹性变形只发生在沟道接触处,基于赫兹接触理论分析了轴承的承载特性。Daidié A、 Chaib Z[2]等研究了一种采用非线性弹簧来等效沟道接触的有限元分析方法,大大缩短了有限元计算时间。Olave M、Sagartzazu X[3]等在考虑支撑结构刚度的基础上,引入刚度矩阵,研究了柔性支撑下轴承的承载特性。芮晓明、郑辉[4]等应用弹性力学理论研究了套圈径向变形对轴承载荷分布的影响。张执南[5]等采用轴对称圆形薄板的相关理论与有限元方法结合对轴承刚度进行了研究。
综上所述,一些学者通过刚性假设对轴承做出了研究,而对于大型偏航轴承,它的刚度变形是一个不可忽略的因素,因此刚性假设具有局限性;一些学者采用有限元方法进行了研究,但由于轴承较大网格较多,往往计算周期长并且很容易不收敛;一些学者采用薄壁圆环理论研究了套圈径向变形对承载特性的影响,但是对于偏航轴承,由于螺栓组在径向提供了很大刚度,径向刚度变形很小,因而薄壁圆环理论也具有局限性。鉴于相关研究的不足,本文采用薄板理论推导了偏航轴承的轴向变形公式,建立了考虑轴向柔性变形的接触载荷求解模型,以2.0MW偏航轴承为例研究了轴承套圈厚度及螺栓分布圆直径对接触载荷的影响。
1 模型构建及求解
1.1 薄板模型的建立
为了便于研究,对轴承进行如下假设:
(1)普通偏航轴承套圈的厚径比约为1/20,因此轴承套圈可等效为环形薄板;
(2)滚道经过淬火处理刚度较大,因此假设滚道在受载后只产生弹性接触变形,沟曲率不变;
(3)假设支撑结构的刚度足够大,受载后支撑结构变形量近似为零。
基于如上假设,在单个螺栓作用力下,轴承内外套圈可以分别等效为由载荷(螺栓力P、螺栓分布圆直径2b)、结构参数(厚度h、节圆直径2a、内孔直径2c)和材料特性(泊松比v、弹性模量E)控制的环形薄板,如图1、图2所示。

图1 内圈

图2 外圈
1.2 薄板模型的边界条件
在滚道处,即r=a处,游隙为零,接触刚度很大(1011级别),接触变形很小(10-5级别),且在游隙为零的情况下,以滚动体中心建立XY平面,忽略接触变形,有:
ωr=a(r,θ)=0
(1)
此外,在滚道(r=a)处的弯矩为零,内圈内端面与外圈外端面(r=c)处的弯矩与剪力为零。边界条件概括如下:
r=a:ω=0,



(2)
1.3 薄板模型的求解
轴承受载后,在小挠度变形分析时,认为螺栓拉力Pj始终沿竖直方向。设轴承套圈在极坐标(r,θ)处的轴向变形为ωj(r,θ),轴承套圈的轴向变形基本方程为:
(3)
对于单个螺栓载荷Pj,在r=b处的载荷密度为:
(4)
根据文献[6],Pj的值可由以下公式求得:
(5)
其中,M为轴承承受的综合弯矩,n为螺栓数量,Fz为轴承承受的轴向力,Φj为螺栓位置角。
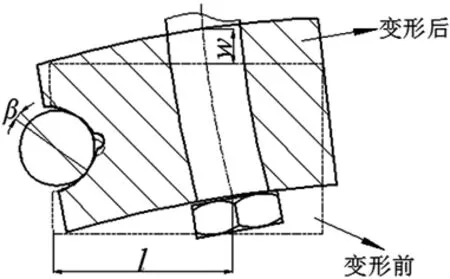
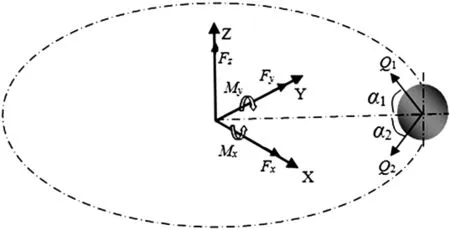
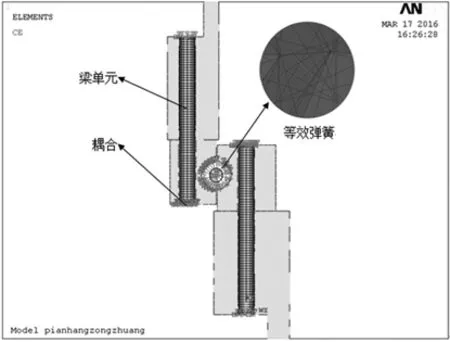
设轴承套圈轴向变形为:
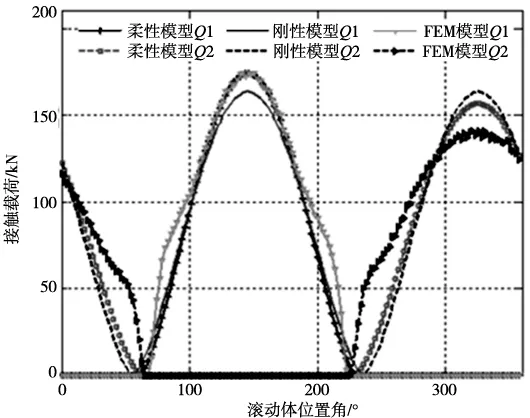
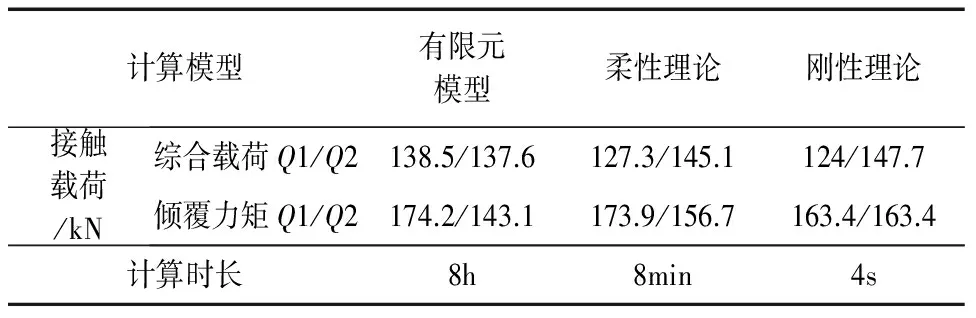
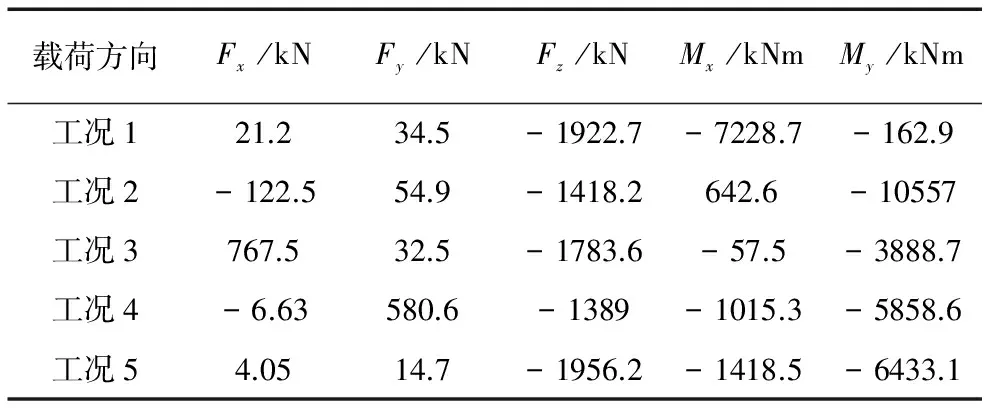
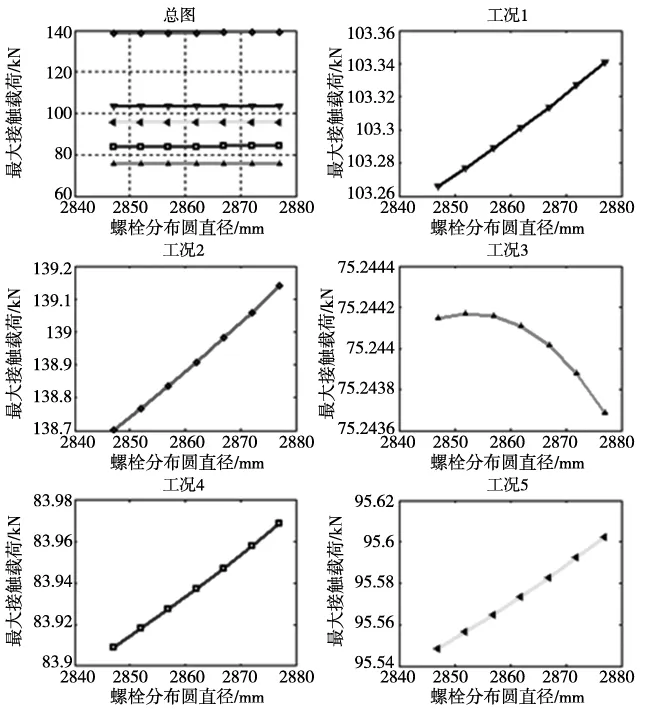
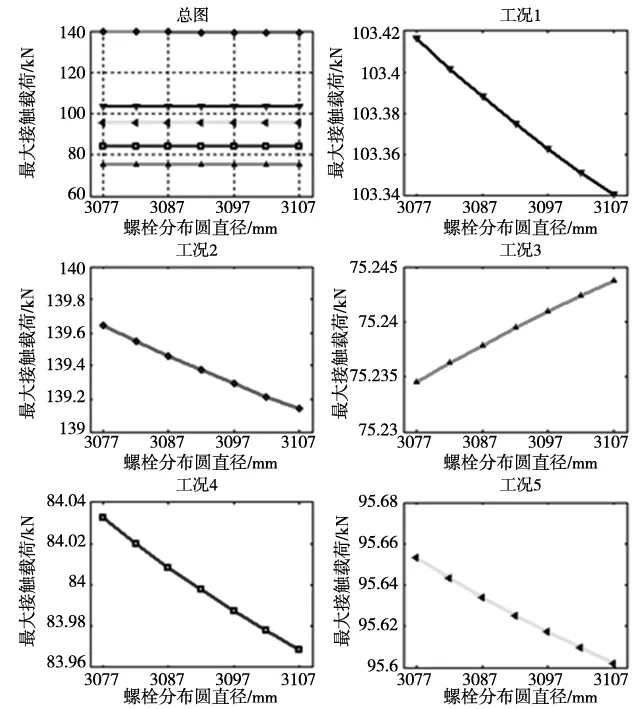
r b (6) 则轴承套圈的轴向变形等式为: ▽4ω1j=▽4ω2j=0 (7) 相应增加的边界条件: (8) 根据以上边界条件及环板边界条件,参考文献[7-8],可以求解出轴承套圈在单个螺栓载荷作用下的轴向变形ωj(r,θ)。 依据叠加原理,轴承套圈在螺栓组整体作用下所产生的轴向变形为: ω(r,θ)=∑ωj(r,θ) (9) 为了考虑支撑法兰的影响,对套圈的挠度变形做出判断:当ω(r,θ)的方向脱离支撑面时,套圈产生轴向变形,大小为求得的值;当ω(r,θ)的方向压向支撑面时,套圈与支撑结构未发生分离,套圈轴向变形与支撑结构轴向变形相等,由于支撑结构刚度足够大,近似有ω(r,θ)=0。 对于单个滚动体,位置角为φi,相对应的在r=b处的套圈轴向变形为: ω(b,φi)=∑ωj(b,φi) (10) 在每个滚动体处,在游隙为零时,套圈的轴向变形使得套圈相对于滚动体产生了一个位置转角βi,从而使接触角产生变化,如图3所示。 图3 滚道偏转 由于βi值很小,近似有: (11) 这样就求出了轴承套圈在受载后绕滚动体产生的变形角βi。 1.4 轴承受载模型的建立与求解 在考虑轴承套圈轴向变形的情况下,为了便于求解,假设套圈先产生轴向变形,然后在载荷作用下做刚体的位移。 轴承套圈轴向变形后,由于接触角的变化,各滚道的曲率中心初始坐标产生了相应的变化,设变形后的初始坐标为r: rpq=T1TpqT2 (12) 式中,p代表下角标“i和o”,分别表示内圈与外圈,q代表下角标“u和d”分别表示上滚道与下滚道,设l为沟道曲率半径与滚动体半径之差,a为节圆半径,φ为滚动体位置角,当q取“u”时,“±或∓”取上,反之取下,有: (13) (14) (15) (16) 假设外圈固定不动,受载后内圈相对外圈发生微小位移u、v、w与偏转φx、φy。依据赫兹接触理论,根据文献[1], 当偏航轴承受到轴向力、径向力、倾覆力的综合作用时 ,其受载模型如图4所示。 图4 受载模型 根据受载情况,建立力学平衡方程,用MATLAB软件采用牛顿-拉夫逊迭代算法,求得该方程组的解。 2.1 有限元模型的建立 本文以2.0WM偏航轴承为例,利用ANSYS分析软件,建立有限元分析模型,轴承的主要结构参数见表1。 表1 轴承主要参数 为了简化模型便于计算,根据文献[3],滚道处采用弹簧等效,螺栓连接采用梁单元,如图5所示。 图5 等效模型 2.2 有限元边界条件 塔架底面全约束;沟道弹簧节点施加周向约束;载荷施加点位于机舱某一位置(相当于风机机舱载荷作用中心),载荷大小由轴承中心载荷做等效处理获得。 偏航轴承在极限载荷作用下,倾覆力矩与轴向力对轴承的轴向变形影响较大,且偏航轴承的一些工况中倾覆力矩几倍于轴向力与径向力。为了充分考虑轴承轴向变形对接触载荷分布的影响及验证柔性理论的适用性,本文以2.0MW偏航轴承为例,分别采用刚性理论[9-10]、柔性理论、有限元方法,分析了轴承在倾覆力矩与综合载荷作用下的接触载荷分布特性,外载荷值见表2。 表2 外载荷值 3.1 计算结果对比 采用不同方法求得的结果如图6和图7及表3所示。 图7 倾覆力矩作用下的接触载荷分布 计算模型有限元模型柔性理论刚性理论接触载荷/kN综合载荷Q1/Q2138.5/137.6127.3/145.1124/147.7倾覆力矩Q1/Q2174.2/143.1173.9/156.7163.4/163.4计算时长8h8min4s 从分析结果可以看出,三种方法分析结果的变化趋势是一致的,接触载荷分布的大小略有不同,柔性理论的分析结果处于有限元分析与刚性分析结果之间;柔性和有限元分析结果与刚性相比,Q1的最大值相对增大,Q2的最大值相对减小,最大接触载荷(Q1最大值 与Q2最大值中较大值)也随之而发生改变,这说明在偏航轴承的分析中,轴向柔性变形对最大接触载荷产生了较大的影响;从计算时长来看,采用柔性理论与刚性理论的效率远远大于有限元分析方法,当进行优化设计时,考虑到计算时间,刚性模型及本文的柔性理论模型相对较为适合。 3.2 轴承套圈厚度的影响 在轴承设计中,轴承套圈的厚度是轴承的一个重要设计参数。基于柔性理论,本文分析了不同套圈厚度的轴承在不同极限工况下的最大接触载荷。考虑到滚动体及其他参数的影响,内圈厚度范围设为110~140mm,对应的外圈厚度为113~143mm;极限工况见表4,分析结果如图8所示。 图8 综合载荷下厚度的影响 载荷方向Fx/kNFy/kNFz/kNMx/kNmMy/kNm工况121.234.5-1922.7-7228.7-162.9工况2-122.554.9-1418.2642.6-10557工况3767.532.5-1783.6-57.5-3888.7工况4-6.63580.6-1389-1015.3-5858.6工况54.0514.7-1956.2-1418.5-6433.1 由分析结果可以看出,在工况2作用下,轴承的接触载荷最大,随着套圈厚度的增加,最大接触载荷先减小后增大,在套圈厚度为120mm时,最大接触载荷取得最小值。在其他工况作用下,最大接触载荷随厚度的变化较小。综合考虑轴承在各种工况下的承载能力,轴承套圈厚度取120mm时,最大接触载荷取得较小值,这与目前2.0MW偏航轴承的厚度较为符合。 3.3 螺栓分布圆直径的影响 一般情况下,螺栓分布圆直径主要根据支撑结构的条件以及螺栓的参数来确定。本文从螺栓分布圆直径对最大接触载荷的影响角度出发,综合考虑其他参数的影响,分别分析了内圈螺栓分布圆直径范围为2842~2877mm,外圈螺栓分布圆直径范围为3077~3107mm,最大接触载荷的变化趋势,从而为螺栓分布圆直径的确定提供参考依据。 施加的工况与3.2相同,分析结果如图9与图10所示。 图9 内圈螺栓分布圆直径的影响 图10 外圈螺栓分布圆直径的影响 由图中可看出,内圈与外螺栓分布圆直径在小范围内变化时,在多数工况下,最大接触载荷随着内圈螺栓分布圆直径的增大有小量的增加,外圈正好相反;工况3作用下的接触载荷与其他工况相比,变化趋势相反,最大接触载荷均小于其它工况,通过表4中各个工况对比可以发现,工况3的倾覆力矩较小,因此,对于承受较大倾覆力矩的偏航轴承,可以忽略工况3分析结果的影响,认为最大接触载荷随着内圈螺栓分布圆直径的增大有小量的增加,外圈与之相反。 (1) 以偏航轴承为例,基于薄板理论与赫兹接触理论,建立了考虑轴向柔性变形的大型偏航轴承接触载荷分析理论模型。 (2) 基于本文的理论模型,以2.0MW偏航轴承为例,分析了套圈厚度及螺栓分布圆直径对最大接触载荷的影响。发现套圈厚度与螺栓分布圆直径对最大接触载荷均有一定影响,综合各种工况,套圈厚度取120mm较为合理;最大接触载荷随着内圈螺栓分布圆直径的增大有小量的增加,外圈正好相反。 (3) 本文的理论模型考虑了轴向变形对接触载荷的影响,与有限元相比,大大缩短了分析时间,为偏航轴承的结构优化设计提供了参考依据。 [1] Zupan S, Prebil I. Carrying angle and carrying capacity of a large single row ball bearing as a function of geometry parameters of the rolling contact and the supporting structure stiffness[J]. Mechanism & Machine Theory, 2001, 36(10): 1087-1103. [2] Daidieé A, Chaib Z, Ghosn A. 3D Simplified Finite Elements Analysis of Load and Contact Angle in a Slewing Ball Bearing[J]. Journal of Mechanical Design, 2008, 130(8): 1188. [3] Olave M, Sagartzazu X, Damian J. Design of Four Contact-Point Slewing Bearing With a New Load Distribution Procedure to Account for Structural Stiffness.[J]. Journal of Vibration & Acoustics. 2010(2): 21001-21006. [4] 芮晓明,郑辉,黄浩然. 风电机组变桨轴承载荷分布研究[J]. 中国电机工程学报,2013,33(32): 80-87. [5] 张执南,丁为民,马会防. 基于板理论的轴承刚度简化模型[J]. 轴承,2015(4):7-11. [6] 陈卓,徐立明. 回转支承[M]. 合肥: 安徽科学技术出版社, 1988. [7] 中原一郎,渋谷寿一.弹性力学手册[M]. 关正西,李跃明,译.西安: 西安交通大学出版社, 2014. [8] 龚良贵,侯瑾,李情. 非轴对称载荷作用下弹性圆形薄板弯曲分析[J]. 南昌大学学报(工科版),2011, 33(1): 38-40, 102. [9] 贾平. 偏航变桨轴承力学特性分析及结构优化设计[D]. 大连:大连理工大学, 2012. [10] T A Harris.滚动轴承分析[M]. 罗继伟,译.北京: 机械工业出版社, 2009. (编辑 李秀敏) Yaw Bearing Contact Load Analysis Based on the Elastic Thin Plate Theory MAO Fan-hai, FAN Jun-kai, DONG Hui-min,WANG De-lun (School of Mechanical Engineering,Dalian University of Technology,Dalian Liaoning 116024,China) Based on the thin plate theory and the Hertz contact theory ,a new computation method is proposed for determining the contact load of the yaw bearing accounting for the axial flexibility deformation of the bearing ring. The results of the mentioned computation method are close to that of the finite element simulation. This method is adopted to analyze the effect of the thickness of the bearing ring and the distribution diameter of the bolts on the contact load of the yaw bearing. The research results shall provide a theoretical basis for the structural optimization design of the yaw bearing. yaw bearing;flexible deformation;contact load; thin plate theory 1001-2265(2017)02-0060-05 10.13462/j.cnki.mmtamt.2017.02.015 2016-04-28; 2016-05-17 辽宁省科技创新重大专项(201303006) 毛范海(1964—),男,辽宁大连人,大连理工大学副教授,研究方向为轴承数字化设计,(E-mail)mao_fh@126.com。 TH133.3;TG506 A
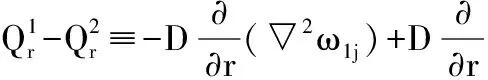

2 有限元分析

3 算例及结果分析


4 结论

