数控机床体积误差激光分步体对角线测量的优化方法*

黄奕乔，杨建国

(上海交通大学 机械与动力工程学院，上海 200240)

数控机床体积误差激光分步体对角线测量的优化方法*

黄奕乔，杨建国

(上海交通大学 机械与动力工程学院，上海 200240)

高精度数控机床已经在市场中广泛应用。为了保证机床在三维空间中的定位精度，需要对机床的体积误差进行测量。文章在传统的激光分步体对角线测量法的基础上，提出了一种简化的辨识方法，通过3条机床工作空间体对角线定位误差的测量数据，即可辨识获得与传统方法(测量4条体对角线)相同的结果，减少了测量时间。针对分步体对角线测量的安装误差，提出了一种优化的测量辨识方法，通过增加3个平动轴定位误差的测量，可以去除安装误差对测量结果的影响，提高了测量辨识精度，同时也不失高效性。运用上述测量方法在机床上实施体积误差测量实验，实验结果证实了文中提出的激光分步体对角线测量的简化方法和优化方法的有效性。

数控机床；体积误差；对角线测量

0 引言

数控机床可以满足了复杂、精密、柔性、智能化的生产需求，是当今生产制造中必不可少的部分。体积精度是衡量机床精度的重要标准。ISO 230-1[1]对机床体积误差进行了定义：在机床工作空间内，刀具在工件坐标系中实际位置和理想位置的最大位置偏差，以及实际姿态和理想姿态的最大方向偏差。为了提高机床精度，体积误差的测量、分析与补偿至关重要[2]。

单项误差元素直接测量法是常用的误差测量方法，各项误差元素可通过激光干涉仪测量[3-4]。运用齐次坐标变换矩阵[5]或螺旋理论[6]等方法建立机床运动学模型，将误差元素合成，获得体积误差。然而单项误差元素测量需要运用很多价格高昂的仪器，并且测量过程复杂，测量时间长。

ISO230-6[7]定义了激光干涉仪体对角线测量法。体对角线测量可以对机床体积精度进行快速评估，但无法进行体积误差元素的辨识。Charles Wang[8]提出了激光分步体对角线测量法，每个平动轴分步运动获得更多的数据，以此分离出体积误差元素。这种方法无需大量昂贵的测量仪器，快速高效。Jiang[9]将该测量方法运用到机床误差补偿中。

Svoboda[10]设计了相关实验，在机床某个平动轴上设置较大的定位误差后，再进行分步体对角线测量，其辨识结果不能准确辨识出该项定位误差，而是将该项定位误差分配在其他平动轴的定位误差上。该实验对分步体对角线法的准确性提出了质疑。Ibaraki[11]认为，安装误差对分步体对角线法的测量精度影响很大。

本文在传统激光分步体对角线法的基础上，提出了一种简化方法和优化方法，测量机床空间的3条体对角线误差和3项定位误差，可以去除安装误差的影响，提高了分步体对角线法的测量精度，同时也不失高效性。运用本文提出的激光分步体对角线测量的优化方法实施体积误差测量实验，实验结果证实了优化方法的有效性。

1 激光分步体对角线测量的简化方法

机床工作空间立方体的体对角线上定位误差可以反映该空间中三个坐标轴方向上的误差影响[12]。以体对角线为例，对角线定位误差ΔR为：

ΔR=e·r

(1)

其中，误差向量e=Δx·ux+Δy·uy+Δz·uz，Δx、Δy、Δz分别为X、Y、Z轴的体积误差；ux、uy、uz分别为X、Y、Z轴的单位向量；r为体对角线的单位向量。

Wang[8]提出了的激光分步体对角线测量法，三个平动轴依次单独运动，运动顺序为：X轴运动(ax,0,0)，然后Y轴运动(0,ay,0)，最后Z轴运动(0,0,az)，如图 1所示。通过激光干涉仪和固定在主轴上运动的大面积平面镜完成沿体对角线方向的定位误差测量。

如图 2所示，Wang提出的激光分步体对角线测量法需要测量的4条体对角线分别定义为：

体对角线ppp，X、Y、Z轴分别沿其正方向运动；

体对角线npp，X轴运动方向为负，Y、Z轴运动方向为正；

体对角线pnp，Y轴运动方向为负，X、Z轴运动方向为正；

体对角线ppn，Z轴运动方向为负，X、Y轴运动方向为正。

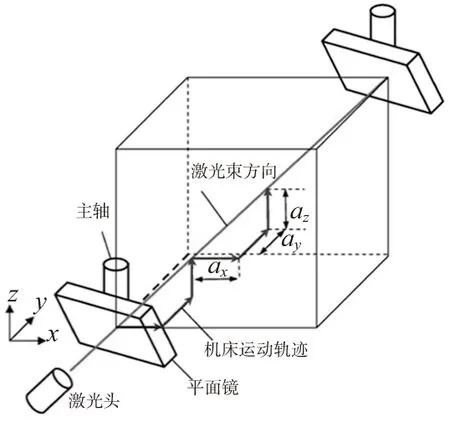
图1 激光分步体对角线测量

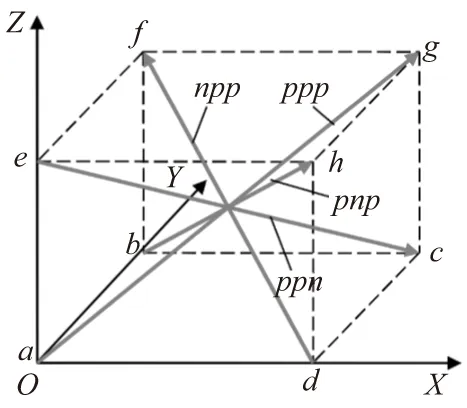
图2 机床工作空间体对角线的命名

Wang[8]提出的传统激光分步体对角线测量法进行误差辨识时，没有明确定义体对角线的运动顺序，也没有考虑单位向量r与误差向量e点乘的正负关系。辨识过程使用了4条体对角线上的分步测量数据，求解12个方程才可以辨识出9项误差的未知量，存在测量数据的冗余和利用不充分。

本文对体对角线的运动顺序进行明确定义，考虑单位向量r和误差向量e的方向关系，提出了简化的激光分步体对角线测量法，只需要测量其中3条体对角线、求解9个方程即可以辨识出9项误差。简化方法充分利用了所有的测量数据，减少了误差检测所需的时间，提升了检测辨识的效率。

本文对激光分步体对角线测量法的测量顺序进行了明确的定义，如图 3所示。沿各坐标轴正方向依次定义[x(1),…,x(n)]、[y(1),…,y(n)]、[z(1),…,z(n)]，沿体对角线的运动方向依次定义[R(1),…,R(n)]。

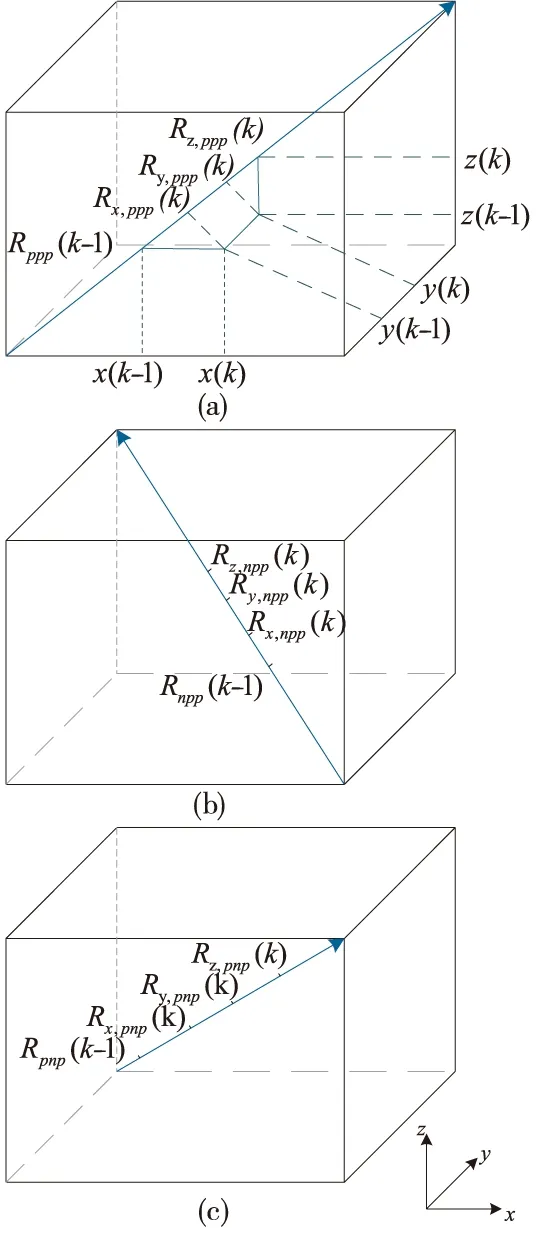
图3 激光分步体对角线测量顺序

如图 3a所示，体对角线ppp第k步(k=1,…，n)运动，从Rppp(k-1)到Rppp(k)，机床依次完成的运动为：

(1)沿X轴从x(k-1)运动至x(k)，运动误差向量ex(k)=[exx(k),eyx(k),ezx(k)]T，exx(k)、eyx(k)、ezx(k)分别为X轴运动时沿X、Y、Z方向的误差，定义误差正方向与坐标系正方向相同；

(2)沿Y轴从y(k-1)运动至y(k)，误差向量ey(k)=[exy(k),eyy(k),ezy(k)]T的定义方式与X轴误差相同；

(3)沿Z轴从z(k-1)运动至z(k)，误差向量为ez(k)=[exz(k),eyz(k),ezz(k)]T的定义方式与X轴误差相同。

体对角线ppp测量误差值为：

(2)

如图3b所示，体对角线npp的运动分析与体对角线ppp类似，其测量误差值为:

(3)

其中，在求解ex(k)时，需要使用第(n-k+1)个体对角线误差数据ΔRx,npp(n-k+1)，其向量乘积取负号。

注释：由于Rx,npp(n-k+1)的表达式为：

Rx,npp(n-k+1)=-rnpp·xe(k)=

(ux,-uy,-uz)·[ax+exx(k),eyx(k),ezx(k)]T=

uxax+uxexx(k)-uyeyx(k)-uzezx(k)

(4)

式中，xe(k)为有误差情况下X轴运动向量。因此ΔRx,npp(n-k+1)方程中的向量乘积取负号。

如图3c所示，体对角线pnp测量误差值为:

(5)

其中，在求解ey(k)时，需要使用第(n-k+1)个体对角线误差数据ΔRy,pnp(n-k+1)，向量乘积取负号。

联立式(2)、式(3)和式(5)，可以求得各运动轴运动产生的体积误差值，其中X轴运动产生的误差值为：

(6)

Y轴运动产生的误差值为：

(7)

Z轴运动产生的误差值为：

(8)

2 激光分步体对角线测量的优化方法

激光分步体对角线法的安装误差对测量精度影响较大。安装误差包括两类：激光束实际位置与理想位置的偏差，称为激光束安装误差；平面反射镜实际位置与理想位置的偏差，称为平面镜安装误差。

Wang[8]对这两类安装误差进行了讨论，在角偏误差可以忽略的前提下，安装误差是一个常数。Ibaraki[11]分析了激光束安装误差、平面镜安装误差对测量精度的影响，两种安装误差的影响本质是相同的，都是在机床存在体积误差时，激光束和平面镜偏离理想位置，最终导致测量值不准确。

本文提出一种优化的测量辨识方法，在简化方法的基础上，增加了3项定位误差exx(k)、eyy(k)、ezz(k)的测量，可以消除安装误差的影响。优化方法建立在机床角偏误差可以忽略不计的前提条件下。优化方法的测量路径如图4所示。

首先对优化方法中用到的符号进行定义。在第k步分步体对角线运动中，不存在激光束安装误差和平面镜安装误差的理想状态下，测量辨识获得的体对角线误差分别为ΔRx,ppp(k)、ΔRy,ppp(k)、ΔRz,ppp(k)、ΔRx,npp(k)、ΔRy,npp(k)、ΔRz,npp(k)、ΔRx,pnp(k)、ΔRy,pnp(k)、ΔRz,pnp(k)。

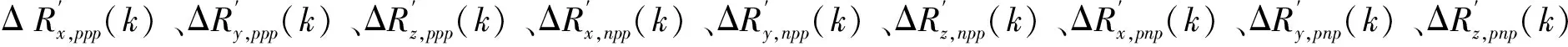
图4 优化的分步体对角线测量

根据Wang[8]的分析，在忽略角偏误差的前提下，安装误差对体对角线测量值的影响与步数k无关，不同步数对应的安装误差值相同。安装误差引起的体对角线误差分别为δRx,ppp、δRy,ppp、δRz,ppp、δRx,npp、δRy,npp、δRz,npp、δRx,pnp、δRy,pnp、δRz,pnp。安装误差对体对角线测量结果的影响为：

(9)

(10)

(11)

将式(9)～式(11)代入式(6)～式(8)，解得：

(12)

(13)

(15)

(18)

(19)

(20)

式(12)～式(20)表示在安装误差存在时，激光分步体对角线法测量辨识的体积误差的表达式。可以看出，安装误差对辨识的体积误差有一定的影响。若想获得机床本身的体积误差值，必须去除安装误差对测量的影响。

为了简化公式的形式，对安装误差的组合进行定义：

(21)

式中δ**表示了式(12)～式(20)中安装误差的组合，m**的下标表示包含该安装误差组合的体积误差项，例如mxx是exx(k)中包含的安装误差组合。在定位误差exx(k)、eyy(k)、ezz(k)直接测量获得之后，代入式(12)、式(16)和式(20)，并对每一步的数据取平均值以消除随机误差，可以解得：

三条坐标轴的测量位置可以任意定义，通常将坐标系定义在三个绝对直线度误差的平均值为零的位置上。即有：

(23)

将式(13)、式(14)、式(19)代入式(23)，可以解得：

(24)

根据Ibaraki的分析[11]，安装误差对单步测量值Rx,ppp、Ry,ppp、Rz,ppp影响较大，对三步体对角线位移误差Rppp、Rnpp、Rpnp影响不大，即：

(25)

将式(25)与式(21)联立，可以解得：

(26)

根据式(22)、式(24)和式(26)，可以解得所有9项安装误差值。将这9项安装误差值代入式(13)～式(19)，可以辨识获得3n项定位误差之外的6n项直线度误差，去除了安装误差对测量结果的影响。图5对优化的激光分步体对角线测量与辨识过程进行总结，其流程步骤为：

(1)分步测量3条体对角线误差；

(2)测量3个平动轴定位误差；

(3)将分步体对角线误差值和定位误差值代入式(22)，解得安装误差mxx、myy、mzz；

(4)将分步体对角线测量值代入式(24)，解得安装误差myx、mzx、myz；

(5)将步骤(3)、步骤(4)中获得的mxx、myy、mzz和myx、mzx、myz代入式(26)中求解，获得安装误差mxz、mxy、mzy；

(6)将安装误差值代入式(13)～式(19)，解得直线度误差eyx(k)、ezx(k)、exy(k)、ezy(k)、exz(k)、eyz(k)。

图5 优化的激光分步体对角线法流程图

3 激光分步体对角线测量实验验证

为了验证本文提出的简化方法和优化方法的正确性，本文进行了激光分步体对角线测量实验。

实验仪器主要包括光动公司(Optodyne)MCV-500激光多普勒测量仪和分步体对角线测量镜组。激光头安装在工作台面上，调整激光束和平面镜的位置，保证激光束与体对角线重合，激光束与平面镜垂直，激光束由激光头发射后能够沿原路线返回。测量仪器的安装如图 6所示。

图6 激光分步体对角线测量

激光分步体对角线法测量的机床工作空间大小为500×400×350mm，4条体对角线的起止坐标位置如表1所示。

表1 体对角线起止坐标位置

每条体对角线的总长度为729.73mm，分为n=10格，每格中进行X、Y、Z分步测量，对应每一步的移动向量为(50,0,0)、(0,40,0)、(0,0,35)。每条对角线正向和反向各测量一次。获得正反向对角线误差的测量结果如图 7所示。可以看出，机床的重复定位精度较好，符合分步体对角线测量辨识的前提条件；机床的体积误差较大。对正反向体对角线测量结果取平均值，代入后续的误差辨识算法中。

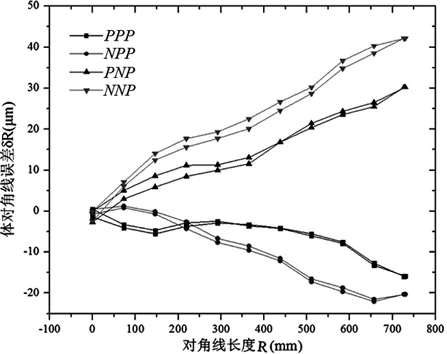
图7 体对角线误差测量值

3.1 分步体对角线测量简化方法验证

首先运用光动的分步体对角线测量软件对测量结果进行数据分析。该软件使用的是传统分步体对角线辨识方法，以X轴的3项误差元素为例，其误差辨识结果如图8中的exx、eyx、ezx曲线所示。

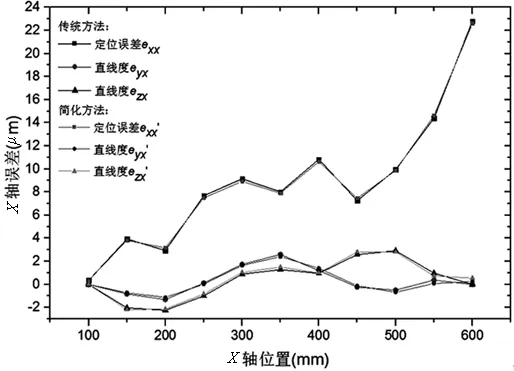
图8 传统分步体对角线法与简化方法的比较

对这一实验结果进行分析可知，简化的激光分步体对角线法的本质与传统分步体对角线测量辨识方法相同。通过准确定义体对角线误差的测量顺序，明确体对角线单位向量与误差向量点乘的正负关系，可以只用3条体对角线的数据实现误差辨识。简化方法的正确性得以验证。

3.2 分步体对角线测量优化方法验证

为了验证本文提出的激光分步体对角线优化方式，使用激光干涉仪对机床X、Y、Z轴的定位误差、直线度、垂直度进行单项直接测量，如图9所示。

将定位误差测量值exx、eyy、ezz和体对角线误差测量值ΔRppp、ΔRnpp、ΔRpnp代入优化的分步体对角线误差辨识方法，获得相应的误差元素项。

由于激光干涉仪进行单项直接测量获得的误差测量值准确度高，将单项测量值作为标准，将单项测量值与优化的分步体对角线辨识值进行比较，可以验证优化的分步体对角线法的有效性。

传统分步体对角线法辨识、优化体对角线法辨识和单项直接测量三种方法获得的误差元素数据如图10～图12所示，并汇总在表 2中。

图9 激光干涉仪测量单项误差元素

其中，在直线度和垂直度的数据处理时，使用最小二乘法拟合得到直线度测量值的最小二乘平均直线，直线度测量值与最小二乘平均线的差值即为调整直线度。垂直度误差值由exy与eyx、exz与ezx、ezy与eyz的最小二乘平均线夹角计算获得。

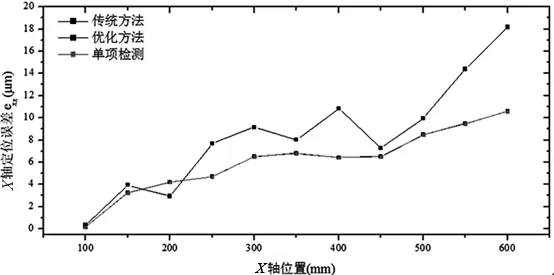
(a)X轴定位误差exx测量与辨识值

(b)X轴直线度误差eyx测量与辨识值

(c)X轴直线度误差ezx测量与辨识值

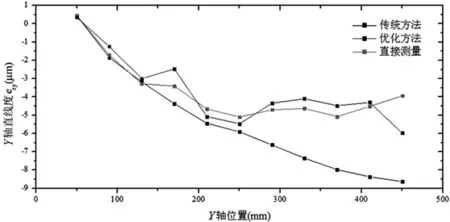
(a) Y轴直线度误差exy测量与辨识值

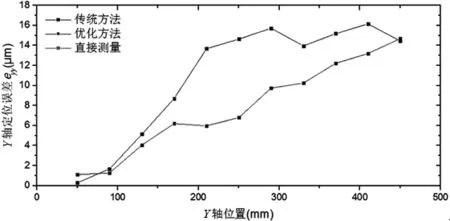
(b) Y轴定位误差eyy测量与辨识值

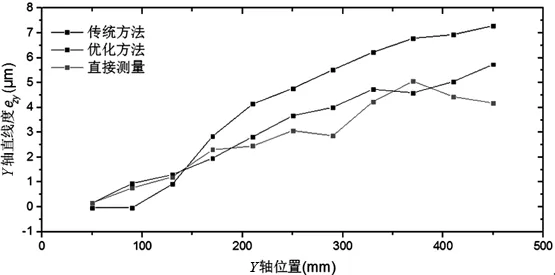
(c) Y轴直线度误差ezy测量与辨识值

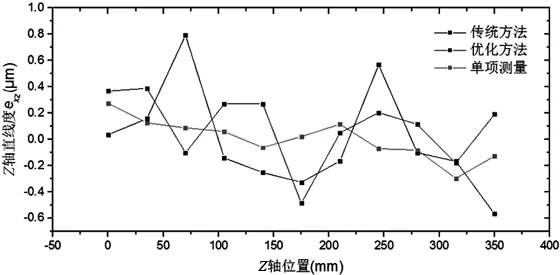
(a) Z轴直线度误差exz测量与辨识值

(b) Z轴直线度误差eyz测量与辨识值

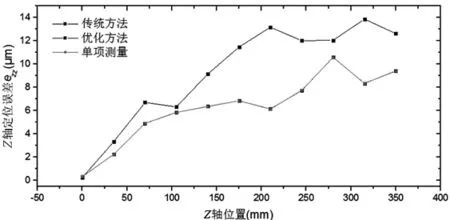
(c) Z轴定位误差ezz测量与辨识值图12 测量和辨识的Z轴误差值

由图10～图12和表2可以看出，相比于传统的分步体对角线的辨识结果，优化的分步体对角线的辨识结果更接近于各误差项的直接测量值。这一现象在被测误差值较大时尤为明显，例如eyx、ezx、exy、ezy的误差辨识结果。因此，优化方法有效的提高了体对角线法误差辨识的精度。

通过测量实验进行的时间来看，平动轴误差单项直接测量的实验时间为13h；传统的激光分步体对角线测量法的实验时间为2.5h；优化的激光分步体对角线测量法的实验时间为4.5h。虽然优化方法比传统分步体对角线法测量路径多，测量时间更长，但与单项直接检测相比，优化的分步体对角线法依然节省了很多测量时间，保证了测量的高效性。

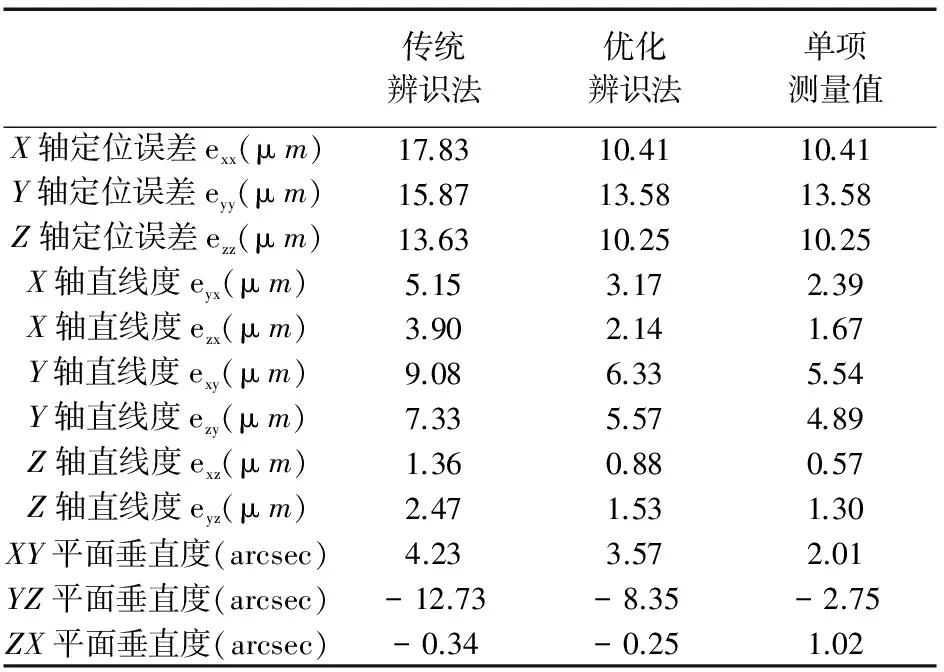
表2 误差元素的辨识值与直接测量值

4 结论

本文在机床体积误差激光分步体对角线检测技术的基础上，提出了简化和优化方法。简化辨识方法根据3条机床工作空间体对角线定位误差的测量数据，即可辨识获得与传统方法(测量4条体对角线)相同的结果，减少了测量时间。优化测量辨识方法通过增加3个平动轴定位误差的测量，可以去除安装误差对测量结果的影响，提高了测量辨识精度，同时也不失高效性。在机床上进行测量实验，实验结果证实了本文所提出的测量辨识方法的有效性。

[1] ISO 230-1:2011. Test code for machine tools - Part 1: Geometric accuracy of machines operating under no-load or quasi-static conditions[S].2011.

[2] 张毅,杨建国,李自汉. 基于自然指数模型的机床定位误差建模与实时补偿[J]. 组合机床与自动化加工技术, 2013(8): 8-11.

[3] Okafor A C,Ertekin Y M. Vertical machining center accuracy characterization using laser interferometer: part 2. Angular errors[J]. Journal of materials processing technology, 2000, 105 (3): 407-420.

[4] Okafor A C,Ertekin Y M. Vertical machining center accuracy characterization using laser interferometer: part 1. Linear positional errors[J]. Journal of Materials Processing Technology, 2000, 105 (3): 394-406.

[5] Okafor A,Ertekin Y M. Derivation of machine tool error models and error compensation procedure for three axes vertical machining center using rigid body kinematics[J]. International Journal of Machine Tools and Manufacture, 2000, 40 (8): 1199-1213.

[6] Moon S K,Moon Y M,Kota S, et al. Screw theory based metrology for design and error compensation of machine tools[A].In Proceedings of DETC[C].2001: 697-707.

[7] ISO 230-6:2002. Test code for machine tools, Part 6: Determination of positioning accuracy on body and face diagonals (diagonal displacement tests)[S].2002.

[8] Wang C. Laser Vector measurement Technique for the determination and compensation of volumetric positioning errors. Part I: Basic theory[J]. Review of scientific instruments, 2000, 71 (10): 3933-3937.

[9] Jiang H,Fan K,Yang J. An improved method for thermally induced positioning errors measurement, modeling, and compensation[J]. The International Journal of Advanced Manufacturing Technology, 2014, 75 (9-12): 1279-1289.

[10] Svoboda O. Testing the diagonal measuring technique[J]. Precision Engineering, 2006, 30 (2): 132-144.

[11] Ibaraki S,Hata T,Matsubara A. A new formulation of laser step-diagonal measurement-two-dimensional case[J]. Precision engineering, 2009, 33 (1): 56-64.

[12] 沈金华. 数控机床误差补偿关键技术及其应用[D]. 上海: 上海交通大学, 2008.

(编辑 李秀敏)

Optimized Method of Laser Step Body Diagonal Measurement of Volumetric Errors of CNC Machine Tools

HUANG Yi-qiao, YANG Jian-guo

(School of Mechanical Engineering, Shanghai Jiao Tong University, Shanghai 200240, China)

The high-precision CNC machine tools have been widely used in the market. To maintain the positioning accuracy in three-dimensional space, it is necessary to measure volumetric errors of machine tools. Based on the conventional laser step body diagonal measurement, a simplified error identification method is recommended. The simplified method could achieve the same results with conventional method with measuring only 3diagonal lines. The time of measurement is saved. An optimized method is proposed according to the research on installation errors of laser step body diagonal measurement. After measuring positioning errors of 3diagonals and 3 translational axes, the installation errors could be removed. With the optimized method, laser step body diagonal measurement becomes more accurate, while the efficiency is still maintained. A measuring experiment for volumetric errors was conducted on a three-axis machine tool. The simplified and optimized methods which are proposed in this paper are validated by the experimental results.

CNC machine tool; volumetric errors; diagonal measurement

1001-2265(2017)02-0054-06

10.13462/j.cnki.mmtamt.2017.02.014

2016-05-13；

2016-06-15

国家科技重大专项(2015ZX04005001)；国家重大科研仪器研制项目(51527806)

黄奕乔(1991—)，男，济南人，上海交通大学硕士研究生，研究方向为精密加工与测试，(E-mail)hyqa01@163.com；通讯作者：杨建国(1956—)，男，上海人，上海交通大学教授，博士生导师，研究方向为精密加工与测试，(E-mail)yang_cnc331@163.com。

TH161；TG659

A