基于Chahine算法的动态光散射颗粒粒度反演

陈文钢，王雪敏，修文正，尹丽菊，申 晋

(山东理工大学 电气与电子工程学院, 山东 淄博 255049)

基于Chahine算法的动态光散射颗粒粒度反演

陈文钢，王雪敏，修文正，尹丽菊，申 晋

(山东理工大学 电气与电子工程学院, 山东 淄博 255049)

采用Chahine算法，在噪声水平分别为0、10-5、10-4、10-3条件下，分别对91nm、253nm和636nm三种单峰分布颗粒的动态光散射数据进行了粒度分布反演.结果表明，在无噪声情况下，对于单峰分布颗粒的粒度分布，通过反演能够得到理想的反演结果.随着噪声水平的增高，反演效果逐渐变差.在同样噪声水平下，随着颗粒粒径的增大，对噪声环境提出更为苛刻的测量要求.因此，Chahine算法适用于噪声较低时的动态光散射颗粒粒度分布反演，尤其适用于单峰分布情况下的中、小颗粒粒度分布的反演.

Chahine算法；反演；粒度分布；动态光散射；

(Using dynamic light scattering DLS)技术是一种测量超细颗粒粒径及其分布的有效方法，已广泛应用于科研和工业等领域[1-2]，该方法是通过散射光强自相关函数获得颗粒粒度及其分布的.由相关函数反演颗粒粒度分布(particle size distribution PSD)需求解第一类Fredholm积分方程，由于其具有高度的病态性，因此，原始数据任何微小的扰动都可能导致所求解与真实解产生巨大偏差.为解决此问题，人们提出多种反演算法，包括累积分析法、指数采样法、双指数法、CONTIN算法、NNLS法及截断奇异值解法等[3-8]，一些改进的反演新方法也不断被提出，每一种算法都有各自的优势与不足. 本文采用Chahine算法进行动态光散射颗粒粒度反演，该算法最初用于大气温度分布测量[9]，是一种非约束算法，不需事先对粒径的分布进行假设，具有迭代格式简单，收敛速度快及精度高的特点.粒度反演结果表明，这一方法反演速度快，适用于动态光散射测量，特别适合在环境噪声较小的实验室测量条件下使用.

1 动态光散射原理与Chahine算法

当一束单色平行光照射样品溶液时，做布朗运动的球形粒子会引起散射光的随机波动.对散射光信号进行自相关运算，得到光强归一化自相关函数[1]

(1)

式中I(t)为t时刻的散射光强，对于平稳随机过程，可取t=0.根据Siegert关系式，可得G(2)(τ)与G(1)(τ)之间的关系式

(2)

式中g(1)(τ)为归一化电场自相关函数；b为G(2)(τ)的基线；β是相干因子.

对于多分散颗粒系，归一化电场自相关函数为

(3)

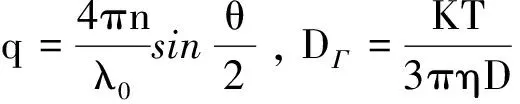
根据式(3)对颗粒粒径进行反演，需对其离散化，离散化后得到的矩阵方程为

Y=AX

(4)

式中，A是M×N矩阵，其元素Aij=exp(-τiΓj)，其中τi对应相关器第i个通道延迟时间，Γj表示离散化后第j级衰减线宽.X=(x1,x2,x3,…,xn)T是离散并归一化后的N×1阶衰减线宽分布向量.Y是g(1)(τ)的离散化形式.

Chahine算法[10]的迭代方程为

F(k)=c(k).*F(k-1)

(5)

F(k-1)是第k-1次迭代得到的颗粒粒度分布，通常采用一个初步优化的粒径分布作为初始分布F(0).c(k)>0为第k次迭代的修正向量且均为正值，且迭代过程为

(6)

式中，上标(k)表示迭代次数，I是测量得到的入射光的电场自相关函数离散化向量，sum表示将矩阵的行向量求和.分析算法步骤可知，每次迭代时所乘的修正因子均为正数，因此，当F(0)为正时，这种方法得到的解具有非负特性.

2 数值模拟

本文选取91nm、253nm和636nm颗粒体系进行数值模拟，对其相关函数进行反演，分析比较反演结果.数值模拟的实验条件：散射角90°，入射光波长632.8nm，分散剂(水)折射率1.331，粘度系数0.8937×10-3N·s·m-2，样品池温度25℃，波尔兹曼常数kB=1.380662×10-23J/K.所加信号噪声为白噪声，噪声水平分别为0、10-5、10-4、10-3.

粒度分布模拟数据用Johnson-SB函数实现

(7)

式中：t为颗粒粒径的归一化尺寸；u和σ是分布参数，改变分布参数可获得不同的粒度分布.定义Xtrue、Xinvert分别为模拟粒径分布和反演粒径分布，为比较Chahine算法性能，引入两个参数：分布误差Error1和峰值相对误差Error2

Error1=‖(Xtrue-Xinvert)‖2

(8)

(9)

式中dmax和d1max分别表示模拟颗粒粒径最大值和反演颗粒粒径最大值.Error1越小，说明反演分布和“真实”分布匹配得越好；Error2越小，说明反演粒径与“真实”粒径的峰值越接近.本文中，“真实”粒径即为模拟颗粒粒径，用“true”表示，反演粒径用“Chahine”表示.

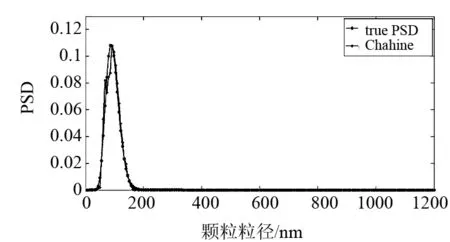
图1 无噪声91nm单峰反演结果

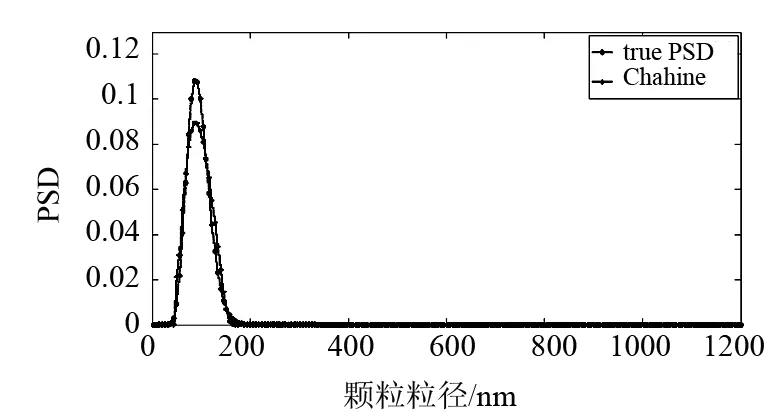
图2 噪声水平为10-5时91nm单峰反演结果

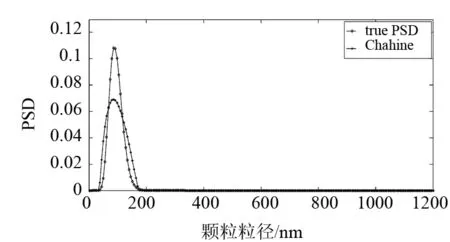
图3 噪声水平为10-4时91nm单峰反演结果

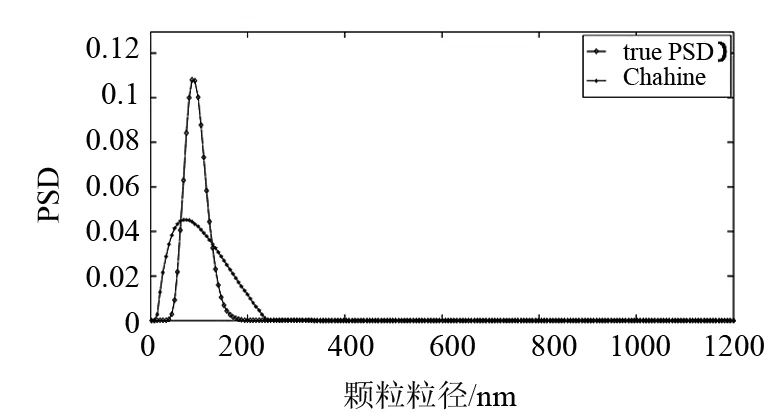
图4 噪声水平为10-3时91nm单峰反演结果

91nm单峰颗粒模拟的分布参数分别为u=0.8和σ=3.0，模拟颗粒粒径范围10～400nm.无噪声情况下反演结果如图1所示，反演结果的分布误差和峰值相对误差分别为0.039 2和0. 在噪声水平分别为10-5、10-4、10-3情况下，粒度分布的反演如图2、3、4所示.三种噪声水平下，分布误差分别为0.048 8、0.102 2和0.170 5，峰值相对误差分别为0、6.59%和19.78%.可以看出，对于91nm单分布颗粒体系，在无噪声情况下Chahine算法可以给出理想的反演结果，随着噪声的增加，反演效果逐渐变差，当噪声水平为10-3时，峰值相对误差可达19.78%.

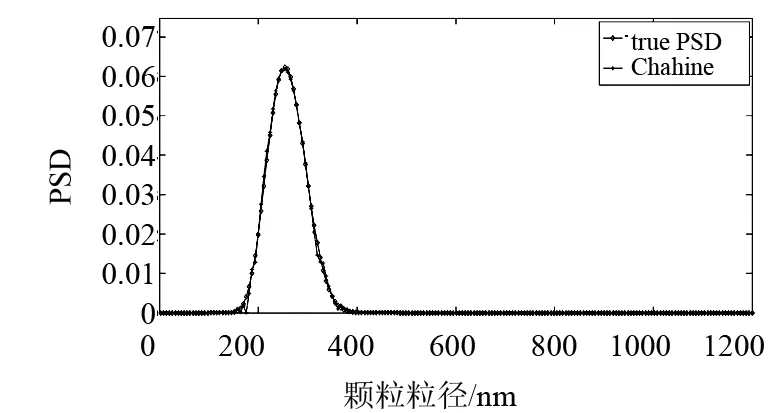
图5 无噪声253nm单峰反演结果

图6 噪声水平为10-5时253nm单峰反演结果

图7 噪声水平为10-4时253nm单峰反演结果

图8 噪声水平为10-3时253nm单峰反演结果

253nm单峰颗粒模拟时，分布参数u=1.8，σ=3.0，模拟颗粒粒径范围100～500nm.无噪声情况下的反演结果如图5所示，分布误差和峰值相对误差分别为0.008 0和0.图6、7、8分别为算法在不同噪声水平下的粒度分布反演，分布误差分别为0.034 9、0.104 9和0.150 7，峰值相对误差分别为0、4.85%和17%.不难看出，在无噪声情况下可以给出理想的253nm单峰颗粒反演结果，随着噪声的增加，反演效果逐步变差.

图9 无噪声636nm单峰反演结果

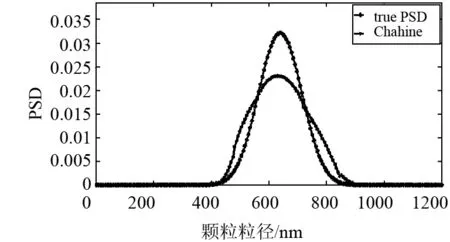
图10 噪声水平为10-5时636nm单峰反演结果

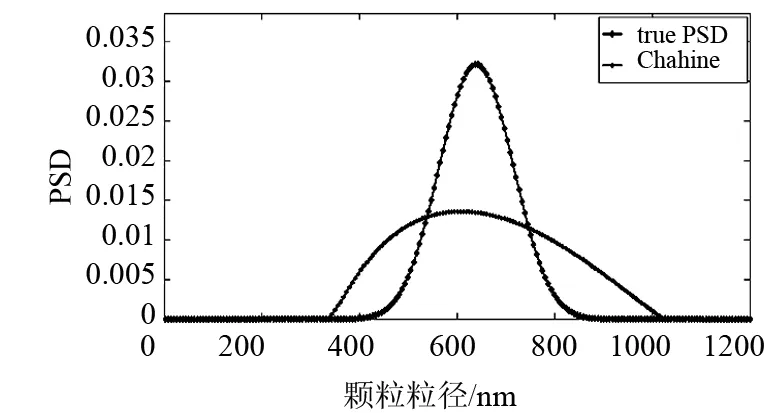
图11 噪声水平为10-4时636nm反演结果

图12 噪声水平为10-3时636nm反演结果

636nm单峰颗粒模拟的分布参数u=0.1，σ=3.7，模拟颗粒粒径范围为100～1200nm.在无噪声情况下，单峰分布反演如图9所示，分布误差和峰值相对误差分别为0.016和0.95%.图10、11、12分别为算法在不同噪声水平下的粒度分布反演，分布误差分别为0.039 9、0.094 3和0.120 6，峰值相对误差分别0.95、5.50%和12.10%.可以看出，对于636nm单分布颗粒体系，在无噪声情况同样可以得到理想的反演结果，随着噪声的增加，反演效果逐渐变差.

3 结束语

本文采用Chahine算法，对模拟的动态光散射数据进行了反演.结果表明，在无噪声情况下，通过反演，对于单峰分布颗粒的粒度分布，能够得到理想的反演结果. 随着噪声水平的增高，反演效果逐渐变差.当噪声水平较低时，反演结果的分布误差和峰值相对误差均能满足测量要求.然而，即使在同样噪声水平下，随着颗粒粒径的增大，反演效果也逐渐变差，对于较大粒径的颗粒，对噪声环境提出较为苛刻的测量要求.因此，本方法适用于噪声较低时的动态光散射颗粒粒度分布的反演，尤其适用于单峰分布情况下的中、小颗粒粒度分布的反演.

[1]DAHANIM,BARRETLA,RAYNALS,etal.Useofdynamiclightscatteringandsmall-angleX-rayscatteringtocharacterizenewsurfactantsinsolutionconditionsformembrane-proteincrystallization[J].ActaCrystallographica, 2015, 71(7): 838-846.

[2]ROGERV,COTTETH,CIPELLETTIL.Anewrobustestimatorofpolydispersityfromdynamiclightscatteringdata[J].AnalyticalChemistry, 2016,88:2 630-2 636.

[3] 刘伟, 王雅静, 申晋. 动态光散射最优拟合累积分析法[J]. 光学学报, 2013(12): 311-318.

[4]MAILERAG,CLEGGPS,PUSEYPN.Particlesizingbydynamiclightscattering:non-linearcumulantanalysis[J].JournalofPhysicsCondensedMatter, 2015, 27(14),145102.

[5]OrsettiS,AndradeEM,MolinaFV.Applicationofaconstrainedregularizationmethodtoextractionofaffinitydistributions:Protonandmetalbindingtohumicsubstances[J].JournalofColloid&InterfaceScience, 2009, 336(2): 377-387.

[6]窦震海, 王雅静, 申晋，等. 动态光散射混合非负截断奇异值反演[J]. 中国激光, 2013(6):264-269.

[7]CHENZ,HUP,MENGQ,etal.NovelOpticalFiberDynamicLightScatteringMeasurementSystemforNanometerParticleSize[J].AdvancesinMaterialsScience&Engineering, 2015, 345(2013): 547-552.

[8]KATOH,NAKAMURAA,OUCHIN,etal.Determinationofbimodalsizedistributionusingdynamiclightscatteringmethodsinthesubmicrometersizerange[J].MaterialsExpress, 2016,6(2):175-182.

[9]GRASS1H.Determinationofaerosolsizedistributionsfromspectralattenuationmeasurements[J].AppliedOptics, 1971, 10(11): 2 534-2 538.

[10]MAOS,SHENJ,ZHUXJ,etal.ModifedRegularizedSolutionofTruncatedSingularValueDecompositionwithChahineAlgorithminDynamicLightScattering(DLS)Measurements[J].LasersinEngineering, 2013, 26(26): 45-47.

(编辑：刘宝江)

Inversion of particle size distribution in dynamic light scattering based on Chahine algorithm

CHEN Wen-gang1, WANG Xue-min, XIU Wen-zheng, YIN Li-ju, SHEN Jin

(School of Electrical and Electronic Engineering, Shandong University of Technology, Zibo 255049, China)

Using dynamic light scattering data based on Chahine algorithm,we invert the particle size distribution for single peak distribution particles (91 nm, 253 nm, 636 nm) with the noise levels of 0、10-5、10-4、10-3. The result indicates that ideal inversion of the PSD for single peak distribution can be obtained in the noiseless case; with the increasing of the noise level, the effectiveness of inversion decreased. With increasing of the particle size, the inversion demands lower noise level of the ambient. Therefore, Chahine algorithm can be applied in the PSD inversion of DLS in low noise level, especially in the inversion of the middle and small particle size with single peak.

Chahine algorithm；inversion；particle size distribution；dynamic light scattering

2016-04-18

山东省自然科学基金项目(ZR2014FL027,ZR2015FL034)

陈文钢，男，baiheshu@ 163.com； 通信作者：申晋，男，shejin@sohu.com

1672-6197(2017)02-0031-04

O

A