有限域上的双循环码

刁玲玉，高 健

( 山东理工大学 理学院，山东 淄博 255049)

有限域上的双循环码

刁玲玉，高 健

( 山东理工大学 理学院，山东 淄博 255049)

设Fq是含有q=pm个元素的有限域，其中p是某个素数，m是正整数．研究了Fq上双循环码及其对偶码的代数结构，以及利用双循环码构造有限域Fq上性能良好的线性码的方法．

双循环码；对偶码；极小生成元集

2010年，Borges等提出了Z2Z4-加性码的概念，并对该加性码的结构与性质进行了初步的研究[1]．此后，该类加性码在工程领域中得到了应用，从而激起了广大编码学者的研究兴趣，涌现出了一些很好的结果[2-3]．2014年，Abualrub等研究了Z2Z4-加性循环码的代数结构[2]．2014年，Borges等将Z2Z4-加性循环码中后半部分的取值换成Z2，即Z2-双循环码[4]并给出了Z2-双循环码及其对偶码的代数结构．本文在文献[4]的基础上对一般有限域Fq上双循环码的代数结构进行研究．

1 有限域Fq上双循环码的代数结构

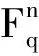
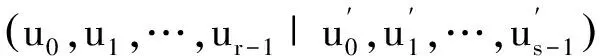
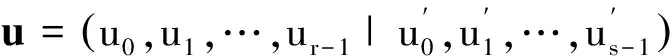
定义

φr:C→Cr

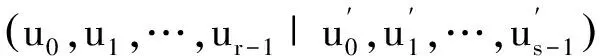
以及

φs:C→Cs

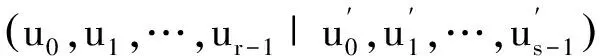
显然，φr与φs是Fq-线性映射．因此，Cr和Cs分别是码长为r和s的q元循环码．如果C=Cr×Cs，则称C是可分的．

定义

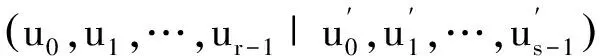
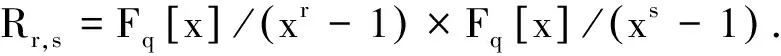
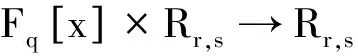
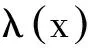
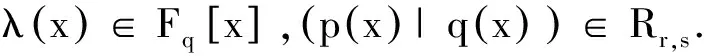
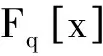
下面〈S〉将表示由Rr,s的一个子集S生成的子模．

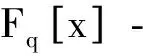
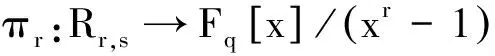
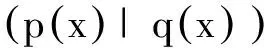
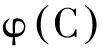
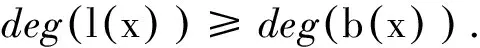
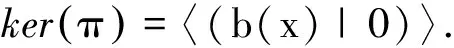
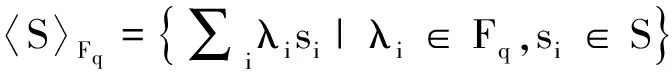
则S1∪S2为C作为Fq-模的极小生成元集．

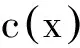
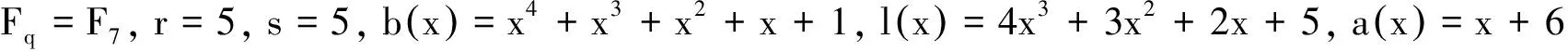
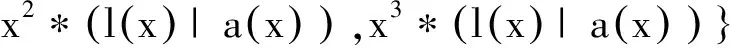
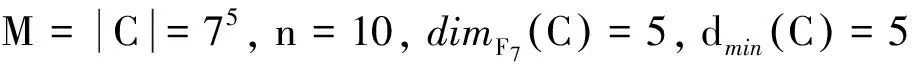
2 双循环码的对偶码

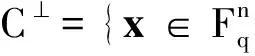
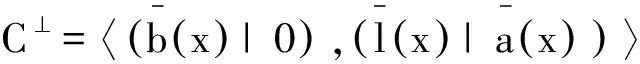
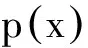
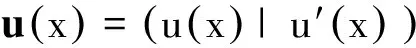
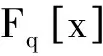
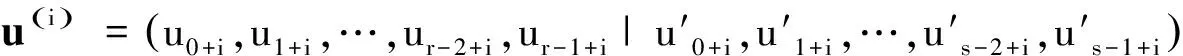
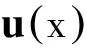
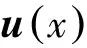
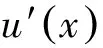
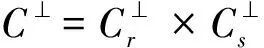
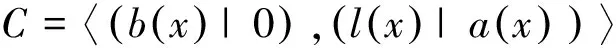
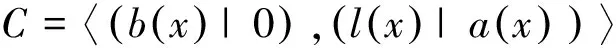
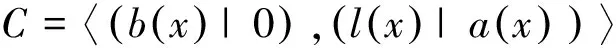
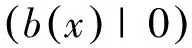
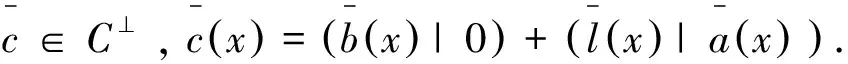
(1)

或

(2)

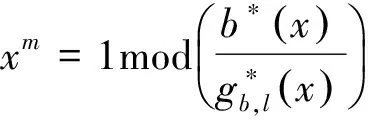
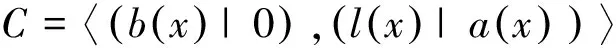
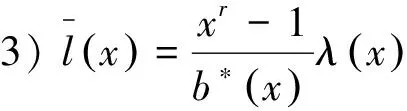
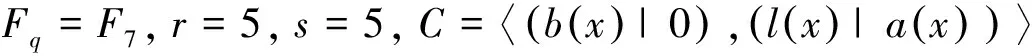
[1]BORGESJ,FERNNDEZ-CRDOBAC,PUJOLJ,etal.Z2Z4-linearcodes:generatormatricesandduality[J].Designs,CodesandCryptography, 2010, 54(2): 167-179.

[2]ABUALRUBT,SIAPI,AYDINN.Z2Z4-additivecycliccodes[J].IEEETransInfoTheory, 2014, 60(3): 1 508-1 514.

[3]GAOJ,SHIM,WUT,etal.OndoublecycliccodesoverZ4[J].FiniteFieldandTheirApplications, 2016(39): 233-250.

[4]BORGESJ,FERNNDEZ-CRDOBAC,TENVALLSR.Z2-doublecycliccodes[J].ComputerScience,2014:arXiv: 1410.5604vl.

[5]HUFFMANWC,PLESSV.FundamentalsofError-CorrectingCodes[M].Cambridge:CambridgeUniversityPress, 2003.

[6]MACWILLIAMSFJ,SLOANENJA.TheTheoryofError-CorrectingCodes[M].NewYork:North-HollandPublishingCompany, 1975.

(编辑：郝秀清)

Doublecycliccodesoverfinitefields

DIAOLing-yu,GAOJian

(SchoolofScience,ShandongUniversityofTechnology,Zibo255049,China)

LetFqbeafinitefieldwithq=pmelements,wherepisaprimeandmisapositiveinteger.Inthispaper,wemainlystudysomestructuralpropertiesofdoublecycliccodesoverFq.Moreover,somegoodlinearcodesareobtainedfromdoublecycliccodesoverFq.

doublecycliccodes;dualcodes;minimumgeneratingsets

2016-06-11

刁玲玉，女，524902388@qq.com

1672-6197(2017)03-0073-06

TN

A