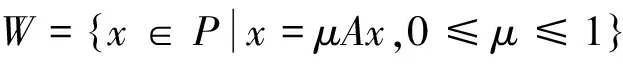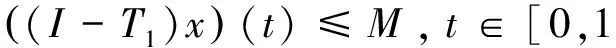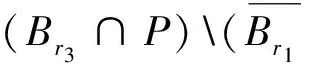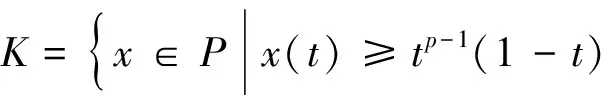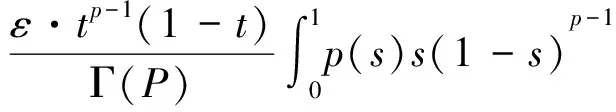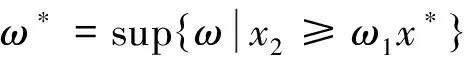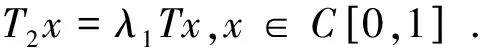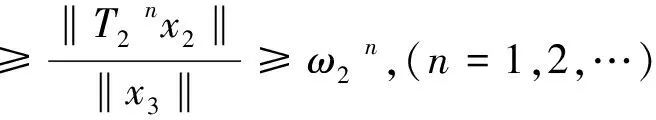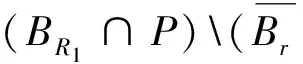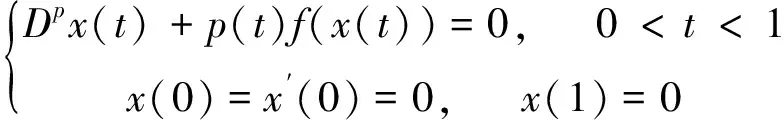分数阶微分方程边值问题的正解
赵 聪,魏帅帅
(1.山东科技大学 数学与系统科学学院, 山东 青岛 266590;2.聊城大学 数学科学学院, 山东 聊城 252059)
分数阶微分方程边值问题的正解
赵 聪1,魏帅帅2
(1.山东科技大学 数学与系统科学学院, 山东 青岛 266590;2.聊城大学 数学科学学院, 山东 聊城 252059)
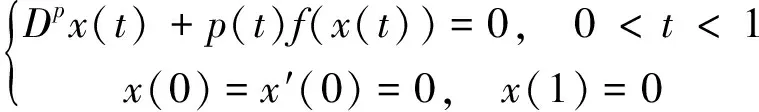
正解;第一特征值;不动点指数
近年来,关于分数阶微分方程边值问题的解已经被众多学者研究[1-8]), 大多数研究证明了分数阶微分方程解的存在性、 唯一性以及它们至少存在一个或多个正解. 例如,文献[4]的作者讨论了边值问题
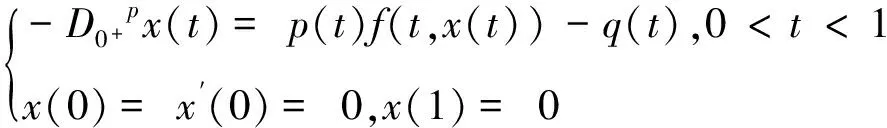
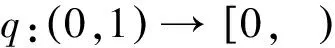
许多作者也通过运用不动点指数、 相应线性算子的第一特征值等理论对非线性微分方程的解进行了研究[9-17], 但将以上两理论结合对解进行研究的方法并未应用于分数阶微分方程. 受到以上文献的启发, 本文将讨论分数阶微分方程边值问题
(1)
至少存在一个正解, 其中2 本文假设以下条件成立: 为了得到本文的主要结果, 给出以下相关定义和引理. 式中n-1≤p 引理1[7]令a∈R,σ∈C(0,1)∩L(0,1)且2 G(t,s)= (2) (i)tp-1(1-t)s(1-s)p-1≤Γ(p)G(t,s)≤ (p-1)s(1-s)p-1,∀t,s∈(0,1) (ii)tp-1(1-t)s(1-s)p-1≤Γ(p)G(t,s)≤ (p-1)tp-1(1-t) , ∀t,s∈(0,1) 定义算子A,T:P→P如下: t,s∈(0,1),x∈E (3) t,s∈(0,1),x∈E (4) 类似于参考文献[9]的引理3可得如下引理. 类似于参考文献[13]可得以下引理. (5) (6) 证明 由(5)式可知: 存在r1>0使得 f(u)≥λ1u, ∀0≤u≤r1 (7) 令x*为T对应于λ1的正特征函数, 则x*=λ1Tx*. 对于任意的x∈∂Br1∩P,根据(7)式有 (8) 不妨假设A在∂Br1∩P上没有不动点(否则结论已成立). 需要证明 x-Ax≠μx*, ∀x∈∂Br1∩P,μ≥0 第二,假新闻泛滥。随着人工智能不断成熟,在制造假新闻这一领域里,AI极有可能成为利益方最好的工具,而媒体正是利益方输送信息最好的渠道。利用人工智能技术进行音视频造假、机器人水军生产大量虚假新闻和评论等等,已形成一个“灰色产业链”,其推动力便是对利益和权力的追求。这一现象在 2016 年美国大选中就有所显现,各种假新闻对总统选举产生了巨大影响,时至今日“通俄门”事件仍在美国发酵。由此发展,AI在未来新闻业的融合极有可能造成假新闻泛滥的局面,这说明未来新闻业的发展或许很大一部分是数据权利的博弈。在这场博弈中,人们看到的世界是真实的世界吗?无疑,新闻的真实性会受到严重的冲击与挑战。 (9) (反证法): 假设存在x1∈∂Br1∩P以及τ0≥0使得x1-Ax1=τ0x*,那么τ0>0且x1=Ax1+τ0x*≥τ0x*.设 (10) 容易看出τ*≥τ0>0且x1≥τ*x*. 根据T(P)⊂P有 λ1Tx1≥τ*λ1Tx*=τ*x* 因此,由(8)式可得 x1=Ax1+τ0x*≥λ1Tx1+τ0x*≥ τ*x*+τ0x* 这与τ*的定义相矛盾, 故(9)式成立, 由引理5可得 (11) 根据(6)式可知, 存在0<η<1以及r2>r1, 使得 f(u)≤ηλ1u, ∀u≥r2 (12) (13) 易知M<+. 令 (14) 下面证明W有界. ∫F(x)G(t,s)p(s)f(x(s))ds+ ∫[0,1]F(x)G(t,s)p(s)f(x(s))ds≤ (T1x)(t)+M,t,s∈(0,1) (15) (I-T1)-1=I+T1+T12+…+T1n+… (16) 根据T1(P)⊂P,有(I-T1)-1(P)⊂P. 因此我们得到x(t)≤(I-T1)-1M,t∈[0,1]. 且W有界. (17) 根据(11)式和(17)式可得 (18) (19) 式中λ1为(3)式中定义的T算子的第一特征值, 那么边值问题(1)至少存在一个正解. 证明 设 那么由引理2的(i)可证得A,T:P→K. 令x*为T对应于λ1的正特征函数, 则x*=λ1Tx*. 从而x*∈K. 根据(18)式可知,当u充分大时, 存在ε>0以及R1>0使得 f(u)≥(λ1+ε)u, ∀u∈[R1,+) (20) 那么存在m>0, 使得f(u)≥(λ1+ε)u-m, ∀u∈[0,+).取 不妨假设A在∂BR1上无不动点(否则结论已成立). 需要证明 x-Ax≠ωx*, ∀x∈∂BR1∩P,ω≥0 (21) (反证法): 假设存在x2∈∂BR1∩P以及ω1>0使得 x2-Ax2=ω1x* 故知x2∈K. 因为T(P)⊂K,x*∈K. 由引理2及(20)式得 x2(t)=Ax2(t)+ω1x*(t)= λ1Tx2(t)+ω1x*(t),t,s∈(0,1) (22) 因此由(22)式, 有 x2≥λ1Tx2+ω1x*≥ω1x* (23) λ1Tx2≥ω*λ1Tx*=ω*x* 那么根据(23)式可以得出 x2≥λ1Tx2+ω1x*≥(ω*+ω1)x* 这与ω*的定义相矛盾, 故(21)式成立, 根据引理5可得 (24) 由(19)式可知,存在0 f(u)≤λ1u, ∀u≤r (25) 需要证明 Ax≠μx, ∀x∈∂Br∩P,μ≥1 (26) (反证法): 假设存在x3∈∂Br∩P以及ω2≥1使得Ax3=ω2x3. 假设ω2>1, 则x3∈∂Br∩P. 由(25)式可得:ω2x3=Ax3≤T2x3. 另外, 有ω2nx3≤T2nx3(n=1,2,…) 即 通过Gelfand公式可以推出 这与r(T2)=1相矛盾, 故(26)式成立, 根据引理6可得 (27) 因此, 由(24)式和(27)式可得 [1]ZHANGS.MonotoneiterativemethodforinitialvalueprobleminvolvingRiemann-Liouvillefractionalderivatives[J].NonlinearAnal, 2009, 71: 2 087-2 093. [2]ZHANGS.Positivesolutionstosingularboundaryvalueproblemfornonlinearfractionaldifferentialequation[J].Comput.Math.Appl, 2010, 59: 1 300-1 309. [3]ZHANGX.Positivesolutionsforaclassofsingularfractionaldifferentialequationwithinfinite-pointboundaryvalueconditions[J].Appl.Math.Lett, 2015, 39: 22-27. [4]CUIY.Uniquenessofsolutionforboundaryvalueproblemsforfractionaldifferentialequations[J].AppliedMathematicsLetters, 2016, 51: 48-54. [5]ZHAOY,SUNS,HANZ,etal.Positivesolutionstoboundaryvalueproblemsofnonlinearfractionaldifferentialequations[J].Abstr.Appl.Anal., 2011(16):6 950-6 958. [6]ZOUY,LIUL,CUIY.Theexistenceofsolutionsforfour-Pointcoupledboundaryvalueproblemsoffractionaldifferentialequationsatresonance[J].Abstr.Appl.Anal, 2014(13):286-299. [7]ZHANGX,LIUL,WUY.Multiplepositivesolutionsofasingularfractionaldifferentialequationwithnegativelyperturbedterm[J].Math.Comput.Modelling, 2012, 55: 1 263-1 274. [8]KILBASA,TRUJILLOJ.differentialequationsoffractionalorder:methods,resultsandproblemsII[J].Appl.Anal,2002, 81: 435-493. [9]LIUZ,LIF.Multiplepositivesolutionsofnonlineartwo-pointboundaryvalueproblems[J].J.Math.Anal.Appl, 1996, 203: 610-625. [10]MAR.Existenceofsolutionsofnonlinearm-pointboundaryvalueproblems[J].J.Math.Anal.Appl, 2001, 256: 556-567. [11]ZHANGG,SUNJ.Positivesolutionsofm-pointboundaryvalueproblems[J].J.Math.Anal.Appl, 2004, 291(2): 406-418. [12]O′REGAND.Theoryofsingularboundaryvalueproblems[M].Singapore:WorldScientific,1994:168. [13]ARIASM,GONZALEZM.Positivesolutionstooperatorequations[formulaomitted] [J].LinearAlgebra&ItsApplications, 2010, 433(6): 1 194-1 202. [14]郭大钧, 孙经先. 非线性积分方程[M]. 济南:山东科技出版社,1987. [15]MAR,ZHANGJ,FUS.Themethodofloweranduppersolutionsforfourth-ordertwo-pointboundaryvalueproblems[J].Math.Anal.Appl., 1997, 215: 415-422. [16]AGARWALR.Onfourth-orderboundaryvalueproblemsarisinginbeamanalysis[J].DifferentialIntegralEquations, 1989(2): 91-110. [17]DEIMLINGK.NonlinearFunctionalAnalysis[M].NewYork:Springer,1985. (编辑:郝秀清) Positive solution for boundary value problems for fractional differential equations ZHAO Cong1,WEI Shuai-shuai2 (1.College of Mathematics and System Science, Shandong University of Science and Technology, Qingdao 266590, China;2.School of Mathematics, Liaocheng University, Liaocheng 252059, China) positive solution; first eigenvalue; fixed point index 2016-09-09 国家自然科学基金项目(11571207) 赵聪, 男,sdustcyj@163.com 1672-6197(2017)03-0011-04 O A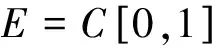
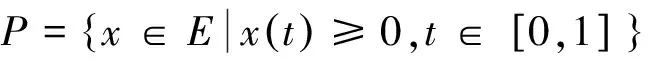


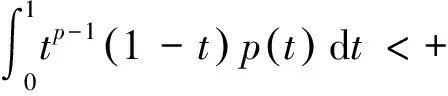
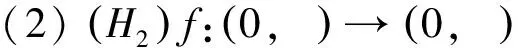
1 预备知识





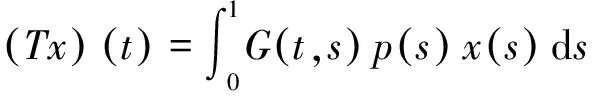
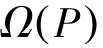
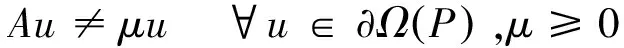
2 主要结果