基于边等距偏移的环切加工刀具路径生成方法

潘海鸿 甘 霖 俞宗薏 陈 琳

1.广西大学机械工程学院，南宁,5300042.广西制造系统与先进制造技术重点实验室，南宁,530004

基于边等距偏移的环切加工刀具路径生成方法

潘海鸿1，2甘 霖1俞宗薏1陈 琳1，2

1.广西大学机械工程学院，南宁,5300042.广西制造系统与先进制造技术重点实验室，南宁,530004

针对由直线和圆弧组成的封闭轮廓生成环切加工刀具路径的问题，提出了一种基于边等距偏移的环切加工刀具路径生成方法。该方法分别从封闭轮廓的凸点和干涉凹点出发，结合边干涉检测程序和圆弧边分段处理方法对包含直线和圆弧的轮廓分别进行局部和全局无效区域检测，删除轮廓的无效区域后进行等距偏移，生成无干涉环切加工路径。利用自主开发的CAD/CAM软件实现了该方法，仿真实验结果表明，该方法能够准确、有效地生成无干涉区域的刀具加工路径，同时适用于带有孤岛的封闭轮廓偏移。

等距偏移；环切；无效区域；干涉检测

0 引言

型腔加工是模具、汽车等领域的零件广泛应用的加工方式之一，其中平面型腔加工最普遍[1]。根据型腔加工的走刀方式可将其分为行切和环切[2]，行切法以一组平行线与加工轮廓组成刀路路径, 相邻两条路径的起点与终点间存在残留高度, 不能满足表面粗糙度要求；环切法按加工轮廓进行多次等距偏移后生成刀具路径，能够保持轮廓的连续性且不需要频繁跳刀，同时具有切削方式不变的优点，可应用于精加工工序。因此，良好的环切刀具路径生成算法能提高型腔加工的效率和精度，在工程上具有重要意义。

为解决封闭轮廓无干涉等距偏移问题，国内外学者做了大量研究，其中包括边等距偏移法[3]、Voronoi图法[4-5]、基于像素(pixel based)法[6]、基于区间算术和四叉树法[7]、基于有效交叉搜索法[8]、基于三角网格曲面法[9]、基于曲面凹凸特征法[10]等，目前以边等距偏移法、Voronoi图法、基于像素法研究为主。Voronio图算法需构建Voronio多边形，实现较为复杂；基于像素法稳定性好，但获取良好的精度时计算量大且内存占用多；边等距法直观且逻辑简单,易于实现。本文基于边等距偏移法对环切加工刀具路径进行研究。

边等距偏移法[3]的基本思路是将原始轮廓等距偏移后用圆弧将断开处连接成封闭轮廓，再对其进行无效区域检测与删除以获得最终偏移线，因此无效区域的检测和删除是边等距偏移法的关键。KALMANOVICH等[11]和ROHMFELD[12]提出了不同的无效区域删除方法，在一定程度上提高了边等距偏移法的可用性，但是仍存在数值不稳定问题。为此，CHOI等[13]用边干涉检测(pair-wise-interference-detection，PWID)程序来检测原始轮廓的无效区域，并将无效区域分为局部和全局无效区域来处理。该方法减少了大量求交运算，提高了算法的数值稳定性，但仅能处理由直线段组成的多边形，而不能直接处理存在孤岛的轮廓。文献[14-15]在文献[13]方法的基础上采用区域网格化获取凹点的干涉边集，将干涉凹点分别作为正负向边，与其干涉边组成两对有向边对，调用PWID进行干涉检测以获取对应全局无效区域，该方法能够直接处理包含孤岛的原始轮廓，但是对于圆弧段仍需采用微小线段拟合。

为了减小边等距偏移法因圆弧段拟合对原始轮廓数量和算法所需时间的影响，本文提出适用于由直线和圆弧组成的封闭轮廓等距偏移方法，该方法结合PWID程序和圆弧边分段处理方法构造局部干涉检测程序，分别以轮廓的凸点和干涉凹点为起点，调用局部干涉检测程序获取对应局部和全局无效区域，最终删除全部无效区域后将轮廓进行等距偏移生成无干涉环切加工路径。

1 术语和定义简述

文中所提出的环切刀具路径生成方法涉及较多定义和术语，其中凹凸点、相切圆、干涉边、干涉关系、干涉点和干涉区间引用文献[13]的相应定义，本节仅对封闭轮廓和方向、边和反射边自行定义。为了便于理解，此处给出干涉关系的定义。

封闭轮廓和方向：本文中讨论由直线和圆弧组成且不存在自交点的封闭二维轮廓。约定沿封闭轮廓方向行进所围成的区域在边的右侧，故外轮廓以顺时针为轮廓方向，内轮廓(孤岛)以逆时针为轮廓方向。

边和反射边：封闭轮廓中由两个顶点连接而成的直线段/圆弧段称为直线边/圆弧边，简称为边，封闭轮廓中的凹点称为反射边。

干涉关系：设封闭轮廓中存在有向边S1和S2，沿偏置方向S1的终点相切圆与S2存在交点，则S1被完全干涉；S1的所有点相切圆均不与S2存在交点，但实际上S1被多边形的其他边干涉，则S1被反向干涉；S1除终点相切圆外其他点相切圆与S2存在交点，则S2被部分干涉。若S1与S2均被部分干涉，则为部分干涉关系；若S1与S2任一被反向干涉，则为反向干涉关系；其他情况S1与S2为完全干涉关系。三种干涉关系如图1所示。

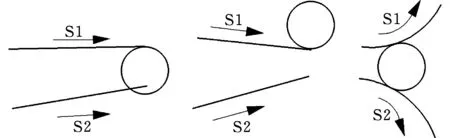
(a)完全干涉 (b)反向干涉(c)部分干涉图1 边与边的干涉关系Fig.1 Interference between edge and edge

2 局部无效区域检测与删除

2.1 原始封闭轮廓顶点处理

封闭轮廓中的顶点按照所在边的顺序编号，便于根据顶点获取对应的有向边进行局部和全局无效区域检测处理。在局部干涉检测之前需对原封闭轮廓的顶点进行分类，根据凹凸点定义，将封闭轮廓的各顶点分类并存放至凹凸点数组中。

2.2 局部干涉检测对圆弧边的处理

从原始封闭轮廓中取任一顶点，沿该点方向与封闭轮廓方向一致称为正向，反之称为负向。记与正向一致的有向边为f_seg，其下一条有向边以f_seg的终点为起点；记与负向一致的有向边为b_seg，其下一条有向边以b_seg的终点为起点。文中将一对正负向边称为有向边对。当封闭轮廓仅存在直线边时，由f_seg和b_seg构成的有向边对分为三种情况，文献[13]中有详细介绍，此处不详述；当包含圆弧轮廓时，则增加了三种有向边对，如图2所示。

文中对存在圆弧的有向边对进行分段处理，实现PWID程序对存在圆弧的轮廓进行局部干涉检测。

PWID程序输入参数为正向及负向有向边的参数f和b、有向干涉边f_seg和b_seg，返回的是一个局部干涉区间的一对端点参数值。程序主要分为以下三部分。

(1)获取正向边f_seg和负向边b_seg。

(2)判断正负边之间的干涉关系，若f_seg与b_seg为完全干涉关系，则完全干涉的边被前进方向的下一条边所替换，并相应地更新f_seg和b_seg；若f_seg和b_seg满足反向干涉关系时，反向干涉的边被其前进方向的下一条边所替换，并相应地更新f_seg和b_seg。

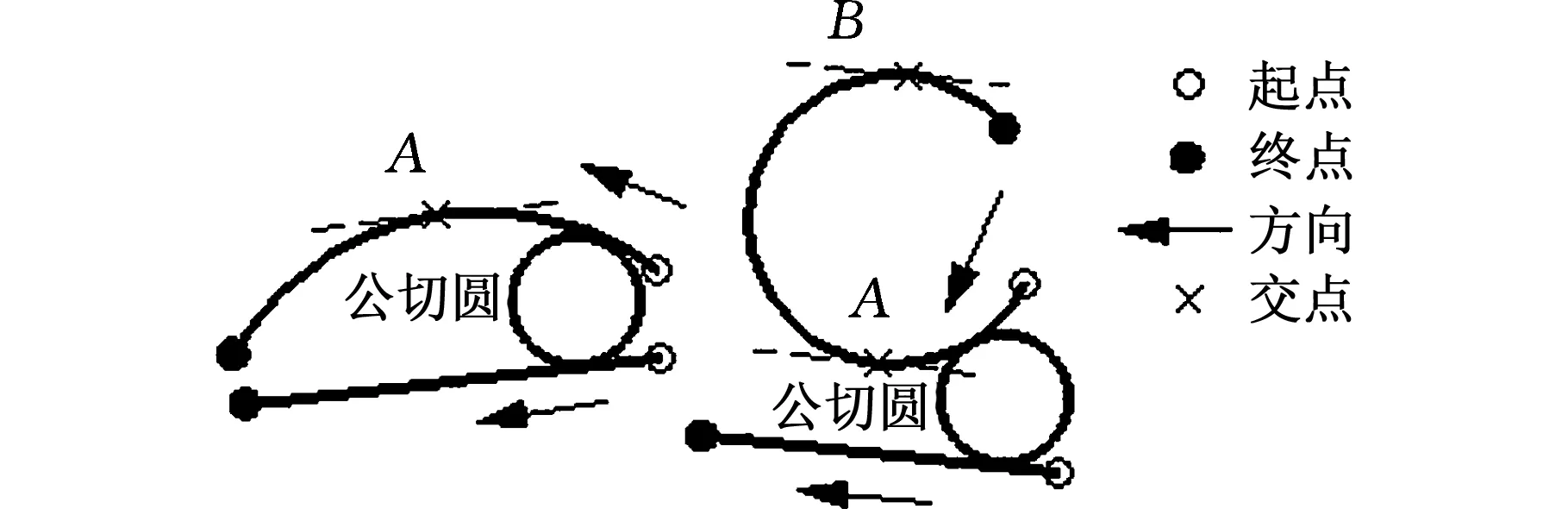
(a)直线、圆弧有向边对

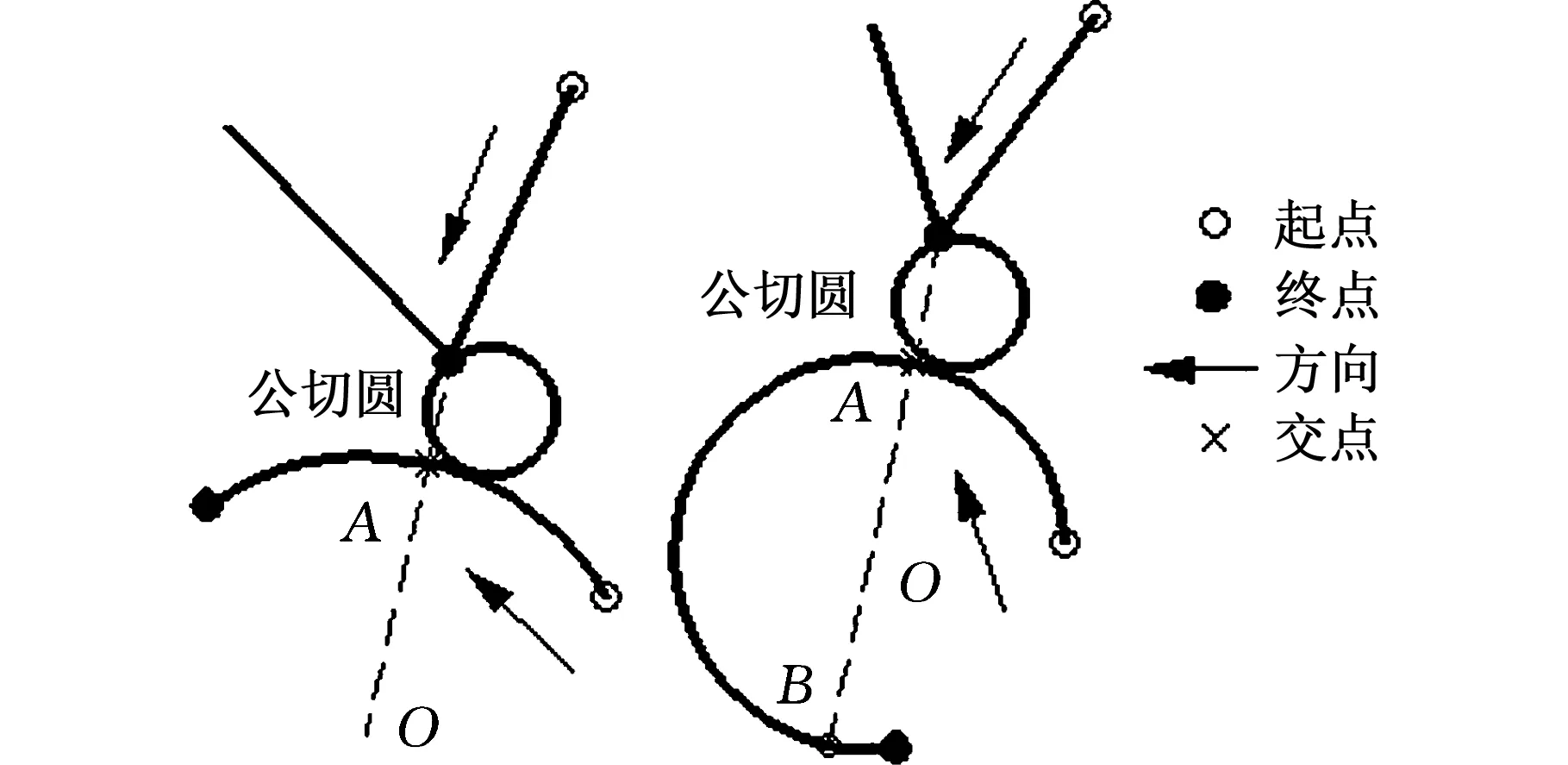
(b)圆弧、反射边有向边对

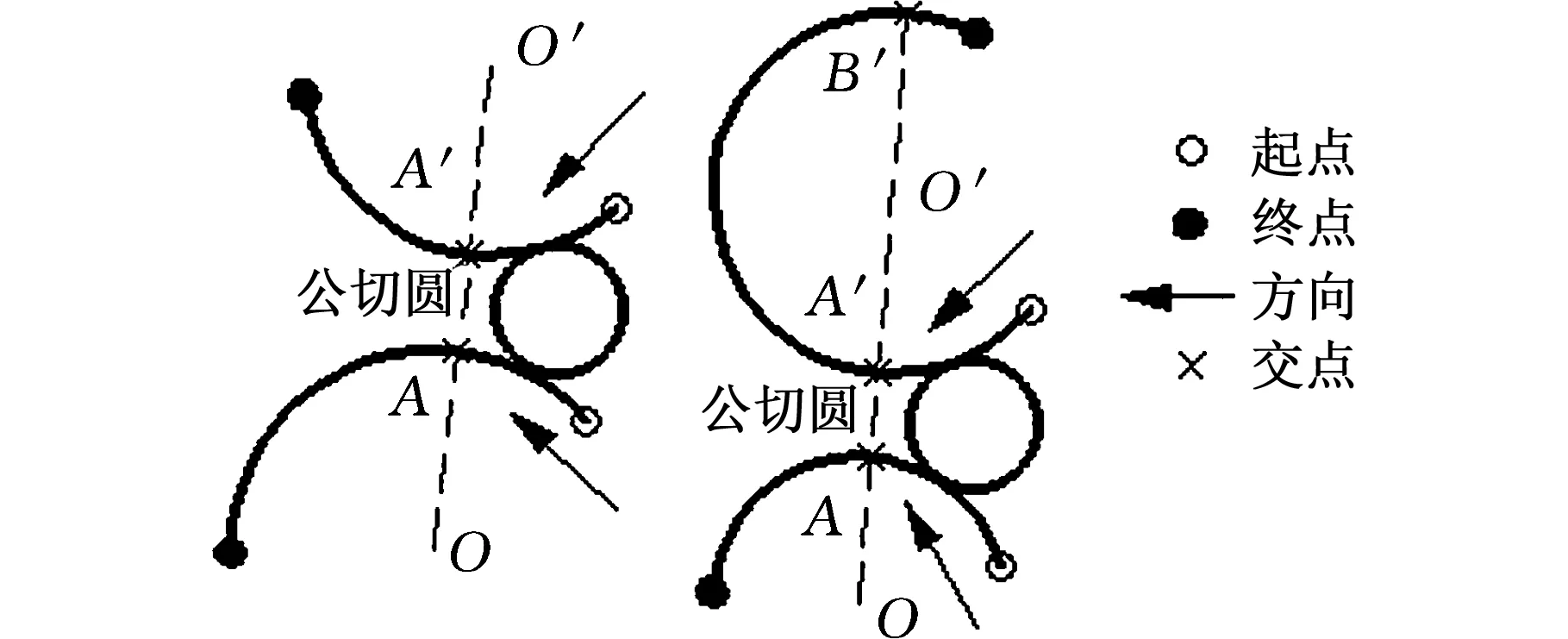
(c)圆弧、圆弧有向边对图2 存在圆弧的有向边对Fig.2 Two directed edges including arc

(3)重复执行步骤(2)操作，直至f_seg和b_seg满足部分干涉关系。当正负向边为部分干涉时，PWID程序返回一个局部干涉区间的一对端点参数值。

根据返回端点值获取端点值对应的正向边f_seg以及反向边b_seg为局部干涉关系。根据两边等距后的边计算公切点参数值，分别赋值给f和b，封闭轮廓中区间[b,f]即为局部无效区域。对封闭轮廓中每一凸点完成PWID程序检测以及根据PWID程序返回参数计算出公切点f和b完成整个封闭轮廓局部无效区域检测。

对于图2a的情况，判断圆弧边是否存在与相对直线边的斜率一致点。若不存在，则按PWID程序进行干涉检测；若存在，以等斜率点(如图2a中点A、B)作为当前圆弧边的分段点，将该圆弧边沿检测时所处方向按顺序分段，并与直线边按PWID程序进行干涉检测。

对于图2b的情况，判断圆弧边是否与反射边和圆弧圆心连线存在交点，若不存在，则按PWID程序进行干涉检测；若存在，以交点(如图2b中点A、B)作为当前圆弧边的分段点，将该圆弧边沿检测时所处方向按顺序分段，并与反射边按PWID程序进行干涉检测。

对于图2c的情况，分别判断两圆弧边是否与两圆弧的连心线存在交点，若不存在，则按PWID程序进行干涉检测；若存在，且交点在圆弧上(不包括圆弧起点或终点，因起点或终点分段后偏移结果为一个点，而非一条边，故不需分段处理)，以交点(如图2c中点A、B、A′、B′)作为当前圆弧边的分段点，将该圆弧边沿检测时所处方向按顺序分段，并与圆弧边按PWID程序进行干涉检测。

在进行局部干涉检测时，若圆弧边需要分段且该圆弧边的偏移方向远离圆心，则将该分段点加入至凹点数组中，待全局无效区域检测时调用。因分段点属于圆弧边，故其对应的有效区间为空。

2.3 局部干涉检测

局部干涉检测的过程是选定任一凸点为起点，取该点相邻的两条边分别作为正负向边，通过不断检测有向边对的干涉关系并替换被干涉边[13]，直至得到存在公切点的有向边对。由直线、圆弧边组成的封闭轮廓局部干涉检测程序实现步骤如图3所示(当有向边对存在圆弧段时，仅以正向边f_seg是圆弧为例)。

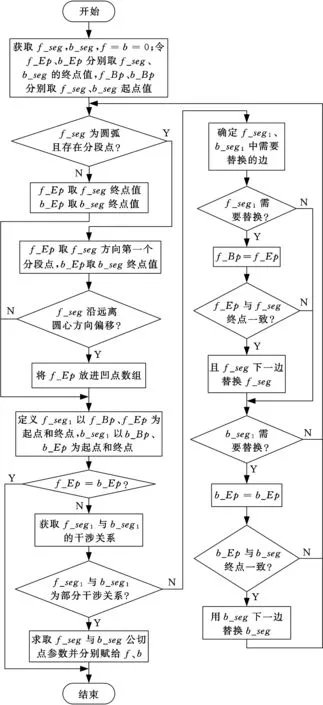
图3 局部干涉检测程序流程图Fig.3 The flow chart of local interference detection

图3中正负向边的干涉关系包括完全干涉、反向干涉和部分干涉。当正负向边不是部分干涉关系时，利用文献[13]中的Replace-full-segment和Replace-reverse-segment程序可得：①若满足完全干涉关系，则替换被完全干涉的有向边。②若满足反向干涉关系，当存在被完全干涉的有向边，则替换被完全干涉的有向边；当存在被部分干涉的有向边，则将被反向干涉的有向边替换，直至所组成的新有向边对不是反向干涉关系；当有向边对均被反向干涉，则正负向边均需要替换。

在局部干涉检测中，正向边f_seg与负向边b_seg在相同的封闭轮廓，故其终点值一致(图3中f_Ep=b_Ep)则表明封闭轮廓不存在有效区域。

2.4 局部无效区域检测与删除

在局部无效区域检测时，将原始封闭轮廓作为输入，调用局部干涉检测程序获取所有的局部无效区域。删除原始封闭轮廓对应的无效区域后，其等距偏移线称为初等偏移线，以用于全局无效区域检测。

局部无效区域检测与删除步骤的主要流程如下：

While(凸点数组中的元素个数不为0)

{

从凸点数组中取出一个凸点并获取其参数值k及对应正负向边f_seg、b_seg；

初始化参数f,b,f_Bp,f_Ep,b_Bp,b_Ep；

调用函数locat_interference_detect，并将变量f，b，f_seg，b_seg，f_Bp，f_Ep，b_Bp，b_Ep作为参数传递：

自原始轮廓中删除局部干涉区域LIR=[b,f]；

从凸点数组中移除所取出的凸点；

}

3 全局无效区域检测与删除

每个全局无效区域对应两个自交点，因此获取其对应的自交点是删除偏移线全局无效区域的前提。文中采用文献[14]的区域网格化方法获取干涉凹点与对应干涉边集，将干涉凹点分别作为正负向边，与其干涉边组成两对有向边对，通过调用两次局部干涉检测函数以确定全局无效区域。文中实现全局无效区域检测时，将原始封闭轮廓的局部无效区域删除，并重新将各边进行参数化作为输入。在全局无效区域检测中，若正向边f_seg与负向边b_seg在同一个封闭轮廓，则其终点值一致表明封闭轮廓不存在有效区域；若不在同一封闭轮廓，则任意一条有向边的替换次数与所在封闭环的段数一致表明封闭轮廓不存在有效区域。

全局无效区域检测及删除的主要步骤如下：

While(输入轮廓中仍存在干涉凹点)

{

取有效凹点作为正向边f_seg；

While(所取干涉凹点仍有干涉边)

{

干涉凹点作为正向边f_seg，其干涉边作为负向边b_seg;

调用函数locat_interference_detect()进行干涉检测，得到f1、b1;

干涉凹点作为负向边b_seg，其干涉边作为正向边f_seg;

调用函数locat_interference_detect()进行干涉检测，得到f2、b2;

获取全局无效区域[b1,f2]∪[b2,f1];

}

从输入轮廓中删除全局无效区域GIR=[b1,f2]∪[b2,f1]；

}

图4所示为对原始轮廓进行局部和全局干涉检测与删除后得到的一次偏移路径，虚线部分为无效区域，[b,f]对应凸点0为起点的局部无效区域， 对应凹点9为起点的全局无效干涉区域。

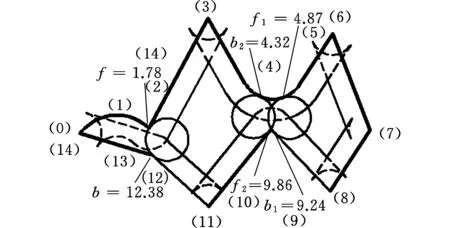
图4 局部与全局无效区域检测图Fig.4 Detection of global and local invalid areas

4 实验验证与讨论分析

为验证基于边等距偏移的环切加工刀具路径生成方法的有效性，在Windows XP系统、2.2 GHz CPU、2 GB内存的环境下，采用基于VC 6.0自主开发的CAD/CAM软件实现该方法，通过两个实例对文中所提出的方法进行验证。图5a是平面钩子图形环切加工刀具路径生成的实例，其轮廓是由直线和圆弧组成的单个封闭轮廓，刀具路径的偏移间距为3.0 mm；图5b是对某零件的环切加工刀具路径生成的实例，其轮廓是由直线和圆弧组成的带孤岛封闭轮廓，刀具路径的偏移间距为3.0 mm。从图5的两个实例图可得本文方法能够准确生成无干涉环切刀具路径。

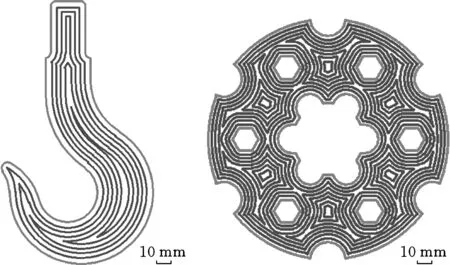
(a)单个封闭轮廓 (b)带孤岛的封闭轮廓图5 基于边等距偏移环切加工刀具路径生成实例Fig.5 Example of contour parallel tool path generation algorithm based on pair-wise offset

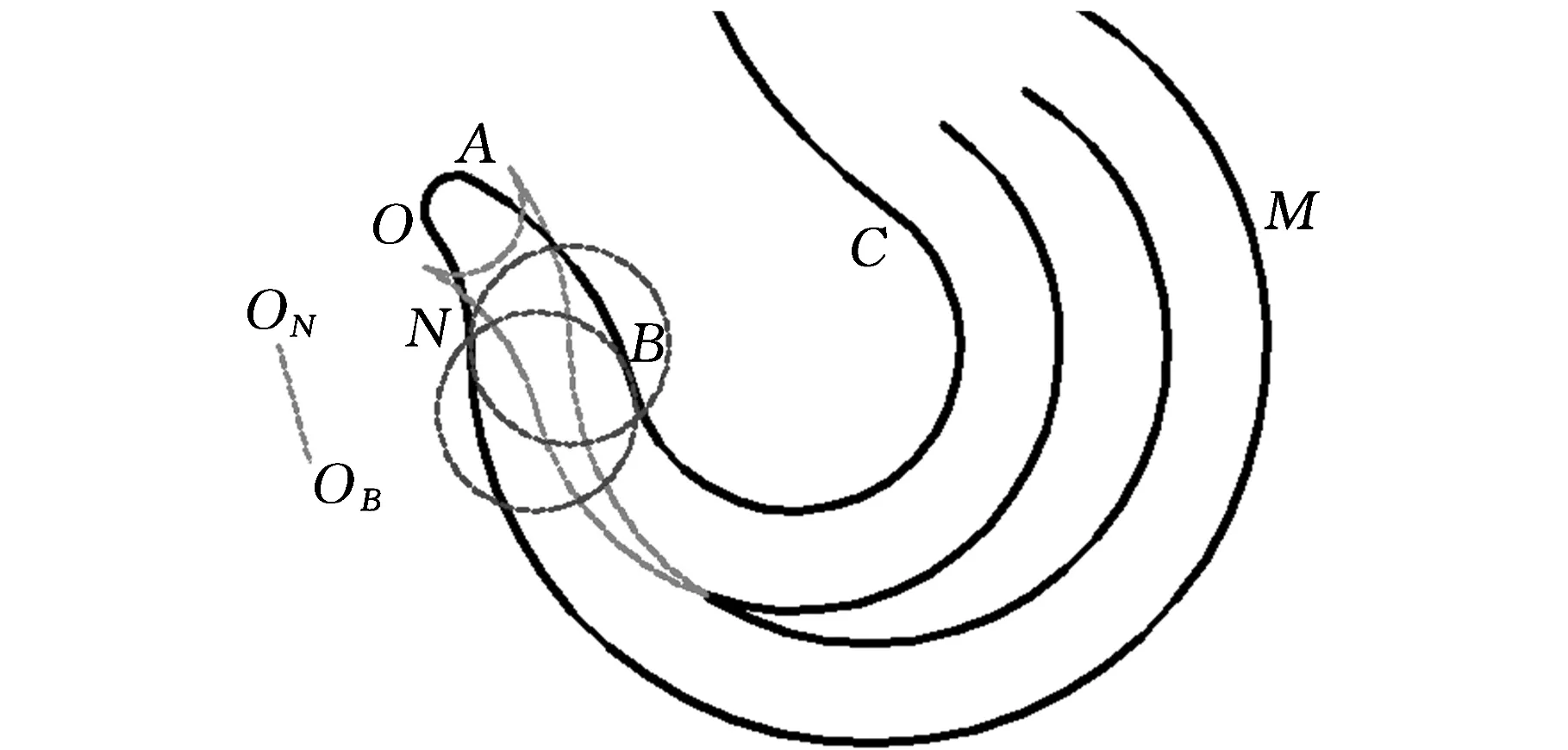
图6所示为图5a中图形的局部干涉情况。全局无效区域由干涉凹点与干涉边组成两对有向边对，调用两次局部干涉检测函数来确定，故文中仅以局部干涉检测为例说明。

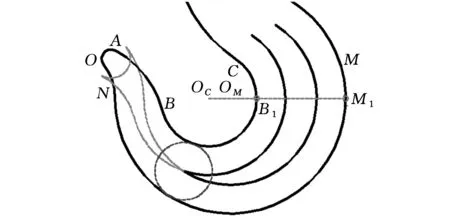
如图6a所示，圆弧AB为正向边，圆弧AO为负向边，连接圆心OA和OB的直线延长线与圆弧AO和圆弧AB相交于点A，因点A为圆弧OA的终点、圆弧AB的起点，故正向圆弧边AB和负向圆弧边AO都不需要进行分段处理。正向圆弧边AB的终点B的相切圆不被负向圆弧边AO干涉，故正向圆弧边AB被负向圆弧边AO部分干涉；负向圆弧边AO的终点O的相切圆被正向圆弧边AB干涉，故负向圆弧边AO被正向圆弧边AB完全干涉。根据PWID程序将负向圆弧边AO替换为圆弧边ON。

如图6b所示，以圆弧AB为正向边，圆弧AN为负向边，连接圆心ON和OB的直线延长不与正负向边存在交点，不符合分段处理条件，故正向圆弧边AB和负向圆弧边AO都不需要进行分段处理，需按PWID程度进行干涉检测。正向圆弧边AB的终点B的相切圆被负向圆弧边AN干涉，故正向圆弧边AB被负向圆弧边AN完全干涉；负向圆弧边AN的终点N的相切圆被正向圆弧边AB干涉，故负向圆弧边AN被正向圆弧边AB完全干涉。根据PWID程序将正向圆弧边AB替换为圆弧边BC，负向圆弧边AN替换为圆弧边NM。

(a)局部干涉检测步骤(1)

(b)局部干涉检测步骤(2)

(c)局部干涉检测步骤(3)图6 图5a加工实例轮廓偏移12 mm后的部分图形干涉检测Fig.6 Partial interference detections of example inFig.5a with 12 mm contour offset

如图6c所示，以圆弧BC为正向边，圆弧NM为负向边，连接圆心OC和OM的直线延长于正向边交于点B1，与负向边交与点M1，故将点B1和点M1作为分段点将正向边分为圆弧边BB1和圆弧边B1C，将负向边分为圆弧边NM1和圆弧边M1M；以圆弧BB1为正向边，圆弧NM1为负向边，连接圆心OC和OM的直线延长不与正负向边存在交点，故正向圆弧边BB1和负向圆弧边NM1都不需要进行分段处理。正向圆弧边BB1的终点B1的相切圆不被负向圆弧边NM1干涉，故正向圆弧边AB被负向圆弧边AN部分干涉；负向圆弧边NM1的终点M1的相切圆不被正向圆弧边BB1干涉，故负向圆弧边AN被正向圆弧边NM1部分干涉。根据PWID程序有向边对为部分干涉关系时，求取其对应的局部干涉参数f=2.34和b=15.74，从而得到局部干涉区域LIR=[15.74,2.34]。

为更好地说明圆弧边的拟合处理和圆弧分段处理对所生成刀具路径结果的影响，使用文中方法对图5实例中的圆弧轮廓进行微小线段拟合，并将其生成刀具路径的运行时间、路径段数与不作拟合处理所得结果进行对比。其中用直线段拟合圆弧时设置弓高误差分别为0.1 mm和0.01 mm以获得两组数据。由表1和表2的结果可以看出当拟合的弓高误差为0.1 mm时，与圆弧分段处理法所用运行时间相差小于0.5 s，其原因是当拟合精度低时，原轮廓拟合后轮廓数量相差较小，故运行时间相近。但是随着拟合精度的提高，采用圆弧分段处理法所得结果在刀具路径段数和运行时间方面的优势更为明显。

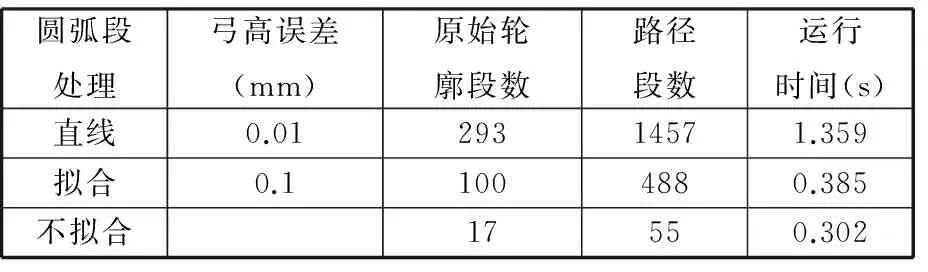
表1 单个封闭轮廓刀具路径生成实例结果对比

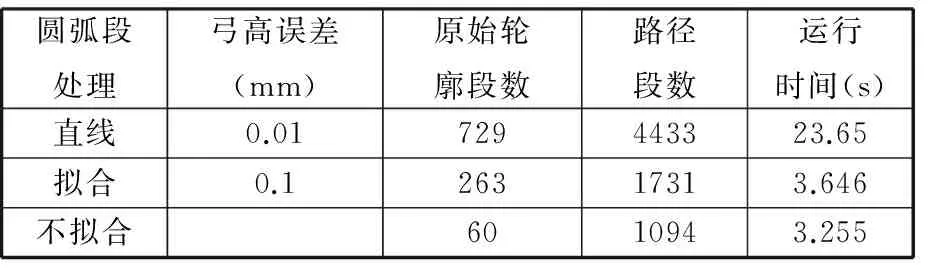
表2 带孤岛的封闭轮廓刀具路径生成实例结果对比

5 结束语

本文提出了一种基于边等距偏移的环切加工刀具路径生成方法，结合PWID程序和圆弧边分段处理方法得到能直接处理包含直线和圆弧的局部干涉检测程序，并用于局部无效区域和全局无效区域的检测。相比文献[13]的方法，本文方法不仅能直接处理轮廓中的圆弧边，还可以直接利用凹点实现对全局无效区域的检测与删除，同时适用于带有孤岛的封闭轮廓等距偏移。仿真结果表明该方法能够准确、有效地生成无干涉的刀具加工路径。

[1] 李骏, 樊留群, 赵建华, 等. 基于区域划分的刀轨生成算法的研究[J]. 组合机床与自动化加工技术, 2014 (5): 123-126. LI Jun, FAN Liuqun, ZHAO Jianhua, et al. Research about Generation Algorithm of Tool Path Based on Area Dividing[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2014 (5)：123-126.

[2] 张鸣, 刘伟军, 李论. 复杂型腔环切清角加工刀轨生成方法[J]. 计算机集成制造系统, 2011, 17(11): 2399-2404. ZHANG Ming, LIU Weijun, LI Lun. Sharp Corner Clean-up CPO Tool-path Generating Method for Complex Pocket[J]. Computer Integrated Manufacturing Systems, 2011, 17(11): 2399-2404.

[3] HANSEN A, ARBAB F. An Algorithm for Generating NC Tool Path for Arbitrary Shaped Pockets with Islands[J]. ACM Transactions on Graphics, 1992,11(2): 152-182.

[4] HELD M. Voronoi Diagrams and Offset Curves of Curvilinear Polygons[J]. Computer-Aided Design, 1998, 30(4): 287-300.

[5] MANSOR M S A, HINDUJA S, OWODUNNI O O. Voronoi Diagram-based Tool Path Compensations for Removing Uncut Material in 21/2D Pocket Machining[J]. Computer-Aided Design, 2006, 38(3): 194-209.

[6] CHOI B K, KIM B H. Die-cavity Pocketing via Cutting Simulation[J]. Computer-Aided Design 1997,29(12): 837-846.

[7] 万健, 徐小媚, 叶晓华. 基于区间算术和四叉树消除偏置曲线自交算法的实现[J]. 计算机应用, 2005, 25(8): 1942-1943. WAN Jian, XU Xiaomei, YE Xiaohua. Eliminating Local and Global Self-intersections of Offsets Based on Interval Arithmetic and Quad Trees [J]. Computer Applications, 2005, 25(8): 1942-1943.

[8] 张嘉易, 郝永平, 刘伟军. 基于有效交叉点搜索的PS边界补偿重建算法[J]. 中国机械工程, 2007, 18(10): 1193-1196. ZHANG Jiayi, HAO Yongping, LIU Weijun. Offset Boundary Reconstruction Algorithm Based on Valid Intersection Points Search[J]. China Mechanical Engineering, 2007, 18(10): 1193-1196.

[9] 孙殿柱, 朱昌志, 崔传辉, 等. 基于三角网格曲面的环切粗加工刀轨生成算法[J]. 华中科技大学学报(自然科学版), 2011 (6): 83-86. SUN Dianzhu, ZHU Changzhi, CUI Chuanhui, et al. Triangular Mesh Surface-based Generation Algorithm of Contour-parallel Rough Tool-path[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2011 (6): 83-86.

[10] 张小明, 王清辉, 王帅. 基于曲面凹凸特征的环切加工轨迹生成方法[J]. 组合机床与自动化加工技术, 2014(3): 134-136. ZHANG Xiaoming, WANG Qinghui, WANG Shuai. Contour-parallel Tool Path Generation Based on Surface Concave and Convex Features[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2014 (3): 134-136.

[11] KALMANOVICH G, NISNEVICH G. Swift and Stable Polygon Growth and Broken Line Offset[J]. Computer-Aided Design 1998,30(11):847-852.

[12] ROHMFELD R F. IGB-offset for Plane Curves—Loop Removal by Scanning of Interval Sequences[J]. Computer Aided Geometric Design, 1998, 15(4): 339-375.

[13] CHOI B K, PARK S C. A Pair-wise Offset Algorithm for 2D Point-sequence Curve[J]. Computer-Aided Design, 1999, 31(12): 735-745.

[14] 陈正鸣, 徐镇全. 一个多边形快速等距偏移方法[J]. 现代制造工程, 2005(12): 7-10. CHEN Zhengming, XU Zhenquan. A Fast Method for Polygon[J]. Modern Manufacturing Engineering. 2005(12), 7-10.

[15] 曹永生. 二维组合曲线的等距方法研究[D]. 南京：河海大学, 2006. CAO Yongsheng. The Research on the Offsetting for 2D-compound Curves[D]. Nanjing:Hohai University, 2006.

(编辑 王旻玥)

Contour-parallel Tool Path Generation Method Based on Pair-wise Offset

PAN Haihong1, 2GAN Lin1YU Zongyi1CHEN Lin1, 2

1.College of Mechanical Engineering,Guangxi University,Nanning，530004 2.Guangxi Key Laboratory of Manufacturing System & Advanced Manufacturing Technology,Nanning，530004

A contour-parallel tool path generation method was proposed based on pair-wise offset to solve the problems of generating contour-parallel tool paths, which were composed of lines and arcs. The convex vertex and interfering concave vertex of closed contour were used as a start point respectively, and the local and global invalid areas of contour including lines and arcs were identified respectively with the method combining pair-wise-interference-detection(PWID) procedures and arc segmentation processing. Non-interference contour-parallel tool path was generated by offsetting the closed contour without invalid area. The proposed method was realized in the self-developed CAD/CAM software. The simulation results show that the tool path without interference area may be generated accurately and effectively with the proposed method, and may be applied to closed contours with islands as well.

pair-wise offset; contour-parallel; invalid area; interference-detection

2016-03-25

国家自然科学基金资助项目(51465005)；广西科技攻关项目(桂科转1599002-16)；广西制造系统与先进制造技术重点实验室项目(14-045-15S09)

TP391

10.3969/j.issn.1004-132X.2017.04.010

潘海鸿，男，1966年生。广西大学机械工程学院教授、博士研究生导师。主要研究方向为复杂机电系统的机电控制理论及方法、全数字网络化交流伺服驱动电机控制理论与技术、自主核心技术支持CAD导航的六自由度关节型机器人。发表论文60余篇。甘 霖，男，1991年生。广西大学机械工程学院硕士研究生。俞宗薏，女，1990年生。广西大学机械工程学院硕士研究生。陈 琳(通信作者)，女，1973年生。广西大学机械工程学院教授。E-mail：gxdxcl@163.com。