面向动力锂电池内部视电阻率三维反演成像方法

谢烁熳，许维蓥，洪晓斌

（华南理工大学机械与汽车工程学院，广东 广州 510640）

面向动力锂电池内部视电阻率三维反演成像方法

谢烁熳，许维蓥，洪晓斌

（华南理工大学机械与汽车工程学院，广东 广州 510640）

为满足电阻层析成像方法应用于动力锂电池内部结构状态监测的精度与实时性要求，提出一种三维电阻层析成像反演算法。针对高斯-牛顿算法的特点，对标准高斯-牛顿算法施加光滑约束，使迭代步长在保证收敛的情况下达到最优化。根据动力锂电池内部视电阻率三维反演成像实验获得的测量结果，研究常规高斯-牛顿算法和光滑约束高斯-牛顿算法的反演能力。结果表明：光滑约束高斯-牛顿算法收敛快，提高了检测效率，能够反映动力锂电池内部的视电阻率变化趋势，并对动力锂电池内部的视电阻率分布做出有效评估。

视电阻率；三维图像反演；高斯-牛顿算法；动力锂电池

0 引 言

动力锂电池是理想的储能元件，得到社会各界的高度关注，其测试与评估已经成为研究热点。动力锂电池的测试与评估主要包括寿命评估、安全性能评估等，其中对于安全性能的测试与评估被广泛开展，例如，Oh S H等[1]研究了循环应用下正极材料与电池安全性能的关系；McCleary等[2]通过建立模型探索了环境温度对锂离子电池安全性的影响；于申军等[3]研究了内阻差异对不同连接方式动力锂电池组安全性能的影响。然而，对于动力锂电池由内部结构变化引发的安全隐患的筛查尚未适应其安全性能评估的要求。

电阻层析成像技术能够利用相应的图像重建算法，非侵入性地重建被测物场的介质分布图，获取物体截面相分布的微观信息，在地质勘查、石油化工、冶金等国民经济行业中有着广泛的应用前景。其中，作为该技术主要参数指标的电导率/电阻率能够完整反映被测物场的介质构成，进而能够对被测对象的内部状态进行状态评估。电阻率与动力电池内部构成的物理化学特性密切相关[4]，物理化学特性发生变化时视电阻率分布相应呈现出变化。通过实时监测动力电池内部视电阻率变化可以对电池在不同使用环境、不同使用条件下的失效进行分析。

图像反演算法的精度和速度是电阻层析成像技术成功应用的关键之一，各国学者基于各种图像反演算法做了大量研究工作。目前，二维图像反演技术已经发展成熟，但其成像目标局限于一系列的二维截面，忽略检测目标几何形状、空间分布等三维信息。因此，发展三维图像反演技术十分必要。三维图像反演研究起步于国外，主要包括数据采集、成像模型、成像算法等方面，例如，Nick等[5]开发了基于EIT的光学材料性能边界测试三维可视化工具包；Zhdanov等[6]建立了基于电磁钻孔测量的井间三维电磁成像模型；Doetsch等[7]利用延时三维表面ERT获知地下水系统状况。目前国内研究主要包括三维图像正演仿真及三维图像反演算法等，徐光捷等[8]采用有限元数值仿真建立三维模型获得ERT传感器敏感场的三维空间分布，分析场域分布的不均匀性；针对ERT成像分辨率低的问题，李守晓等[9]提出基于三维模型的改进Tikhonov迭代电阻成像算法。对于基于ERT技术的三维图像反演，尤其是复杂的动力锂电池内部结构的三维图像反演，目前国内仍很少涉及。本文在前期的采用电阻层析成像技术结合电性能监测电池内部状态的基础上[10]，提出通过三维图像反演算法对视电阻率进行成像，快速判断电池内部状态。

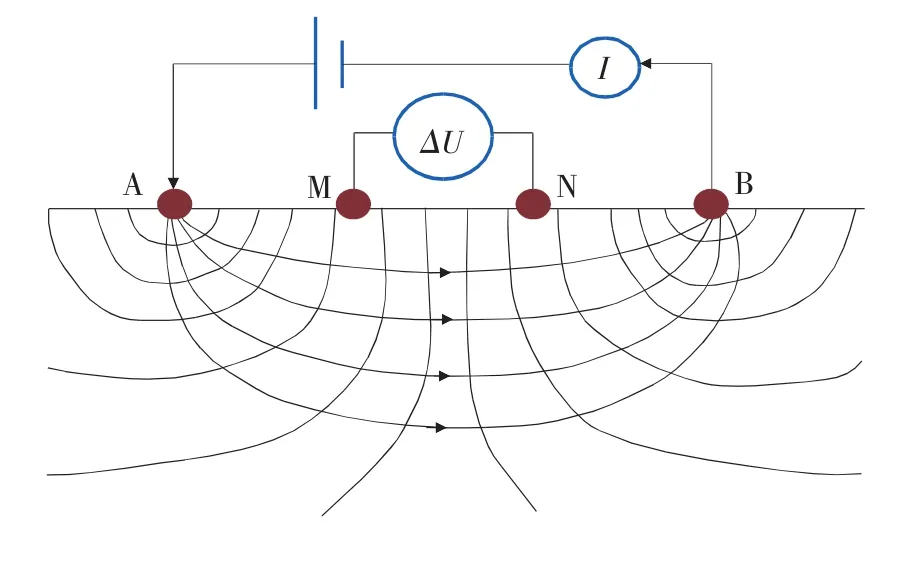
图1 四电极测量原理

1 动力锂电池内部视电阻率测量装置

1.1 测量原理

采用四电极测量原理，如图1所示。在A、M、N、B 4个横向排列的电极阵列中，对激励电极A、B持续施加脉冲电流，从而在电池内部形成稳定电场，测量电极M、N两点间电势差可反映探测区域的视电阻率情况，调整电极间距可有效改变探测深度。定义n为电极间距因子，即电极距AM与MN的比值，测量电极M、N位置保持不变，激励电极A、B等间隔向两边移动，n可依次取1，2，3，…，k。改变测量电极间距MN，以相同方式移动激励电极A、B进行测量可以增加探测深度，尽可能获取电池内部不同区域的信息。

1.2 测量装置

三维视电阻率测量系统如图2所示，包括了三维传感器单元、数据采集单元和图像反演单元。三维柔性传感器[11]主要由高可靠性柔性线路板(FPC)和电极阵列组成。数据采集单元进行信号采集及处理，处理后数据通过CAN总线传输至上位机，上位机对输入数据进行电压-电阻率转换，通过图像反演算法，对电池的内部进行三维图像重建，并构造整体电池组内部视电阻率分布的三维效果图。

2 光滑约束高斯-牛顿三维反演成像算法

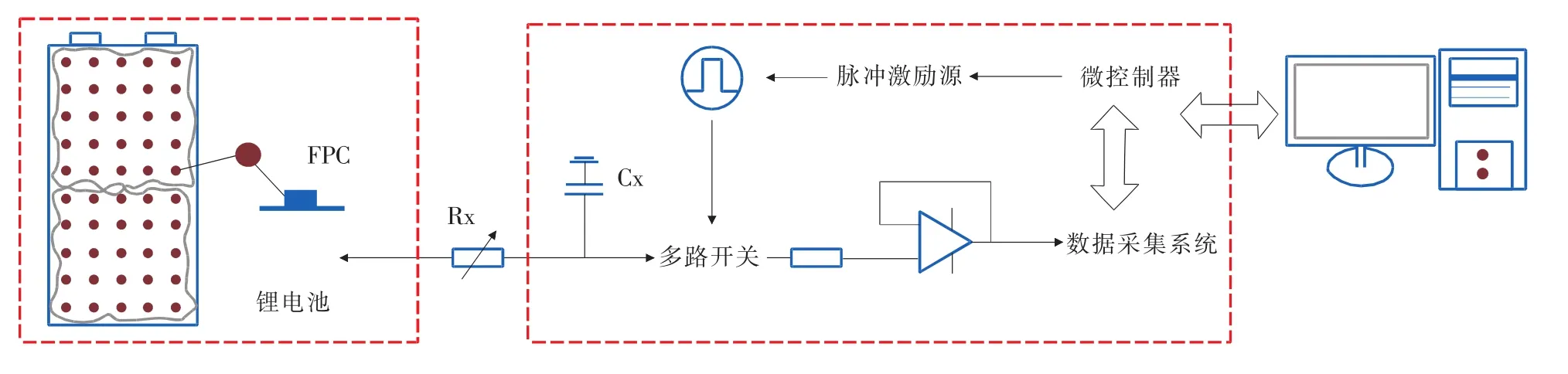
图2 电池三维视电阻率测量系统

动力锂电池内部结构ERT检测技术的反演问题是一个非线性问题，本文在求解过程中将该非线性问题线性化，通过求解线性方程组，获得非线性问题的解。若任意函数f（x）满足级数理论条件，可以用泰勒级数表示在点p的邻域里的函数f（x）：

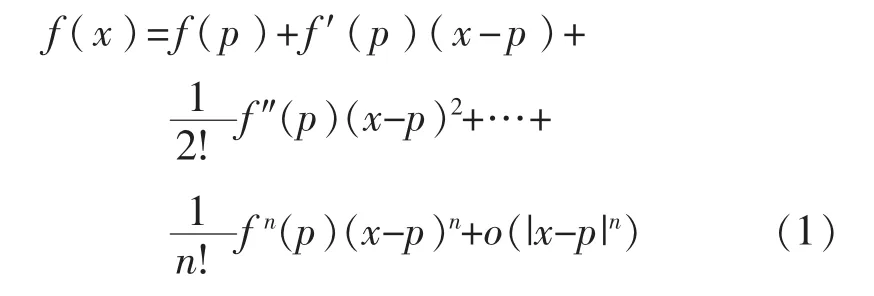
其中o（|x-p|n）表示高阶无穷小，若取函数f（x）的一阶近似为前两项，则有：

忽略一阶无穷小，有：

若x为N维向量，则：

其中：

将式（4）应用于动力锂电池内部结构状态ERT反演非线性问题：

式中：dj——第j个观测数据；

mi——第i个模型参数；

dj0——初始模型的第j个观测数据；

Δmi——mi的增量，Δmi=mi-mi0；

Δdj——dj的增量，Δdj=dj-dj0。

将式（5）写成矩阵：

将式（6）正则化得到原理方程，即：

构造目标函数ψ：

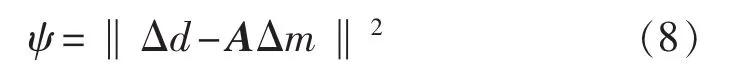
将目标函数对Δm求导并令其等于0，得到：

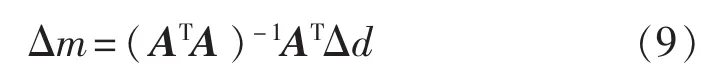
矩阵A为雅克比矩阵，求解式（9）可以得到模型的修正量Δm，将Δm加到起始模型m0得到更接近真实的新向量。然而，M＞N，式（9）是一个超定方程。

矩阵ATA是严重病态的，导致式（9）为病态问题。将光滑约束引入反演方程可以解决这个问题。对于第i个网格而言，光滑约束可以表示为

式中：Δmi——第i个网格的模型参数修正量；

整个模型的光滑约束用矩阵表示为

其中F为光滑度矩阵。

标准高斯-牛顿算法，利用正演模型和实测数据构造一目标函数，并使其达到极小。光滑约束高斯-牛顿算法基于以下方程：

式中：FTF=FxFxT+FzFzT，Fx为水平平滑滤波系数矩阵，Fz为垂直平滑滤波系数矩阵；

u——阻尼系数；

Δm——模型参数修正量；

g——数据残差矢量，其值等于实测电阻率对数值与模拟的视电阻率对数值之差。

二、三维反演过程中对方程式偏导数矩阵的计算方式有所不同，二维反演对应的偏导数矩阵为二维计算，三维反演对应的偏导数矩阵为三维计算，偏导数矩阵的计算方式不同，导致了二、三维反演效果的不同。

通过对方程组进行求解，得到模型参数修正矢量，将其代入下式：

便得到新预测模型参数向量Δm（k）。重复这个过程直至实测数据和模拟数据之间的平均均方误差RMS满足要求为止，电阻率反演过程结束。

3 实验研究

3.1 实验平台

动力电池内部三维视电阻率测量平台如图3所示，实验对象为铝壳磷酸铁锂动力电池，尺寸140mm× 65mm×18mm。电极片为直径5mm、厚度0.6mm圆形铜电极片，电极中心间距为12mm。

试验中，环境温度为常温26.7℃，双极性脉冲电流幅值设定为1mA，幅值增益为1。测试过程中，横向10个电极11个数据点，纵向5个电极2个数据点，5×10电极阵列共有75个数据点，每个数据点重复测量6次。

图3 动力电池内部三维视电阻率测量平台

3.2 性能验证实验

实验将动力锂电池与冰块接触，通过冰块的局部降温使得电池内部的视电阻率分布呈现出与温度变化相对应的变化，通过成像结果与冰块实际放置位置的比较验证成像算法的保真度。

在对未放置冰块的动力锂电池进行数据采集，获取3组数据后，将体积为212.55 cm3的半圆柱体冰块置于电池右侧下方并与之紧密接触，接触面积为70.85cm2，如图4所示。冰块放置后对动力锂电池每隔30s采集一次数据，获取5组数据，随后每隔1min采集一次数据，获取4组数据，共获取9组数据。实验选取了电池的前后左右侧共4个位置放置冰块，每个位置均获取9组数据，实验结果一致。本文仅对其中一组实验结果进行详细描述。

图4 冰块放置示意图

在Matlab平台上将系统输出的电压值换算为视电阻率，然后把各测点的坐标与视电阻率值对应起来，采用光滑约束高斯-牛顿算法对视电阻率进行图像反演，得到动力电池内部的视电阻率分布。

通过式（15）将电压数据转换视电阻率：

电流I为5×10-4A，放大倍数k=5000，参数G不同层数据点取值不一样，第 1层数据点 G=2π· 0.012，第2层数据点G=2π·0.024。电压数据为十六进制，需要换算为十进制，参照式（16）换算。

9组数据的换算结果如图5所示，1～7数据点为第1层数据，8～11数据点为第2层数据，第2层数据点视电阻率明显高于第1层数据点视电阻率，说明随着深度增加，视电阻率上升。在放置冰块1min 30s到2 min之间的30 s内视电阻率发生明显变化，因此选择这两个时刻的数据进行图像反演，通过对比进行分析。

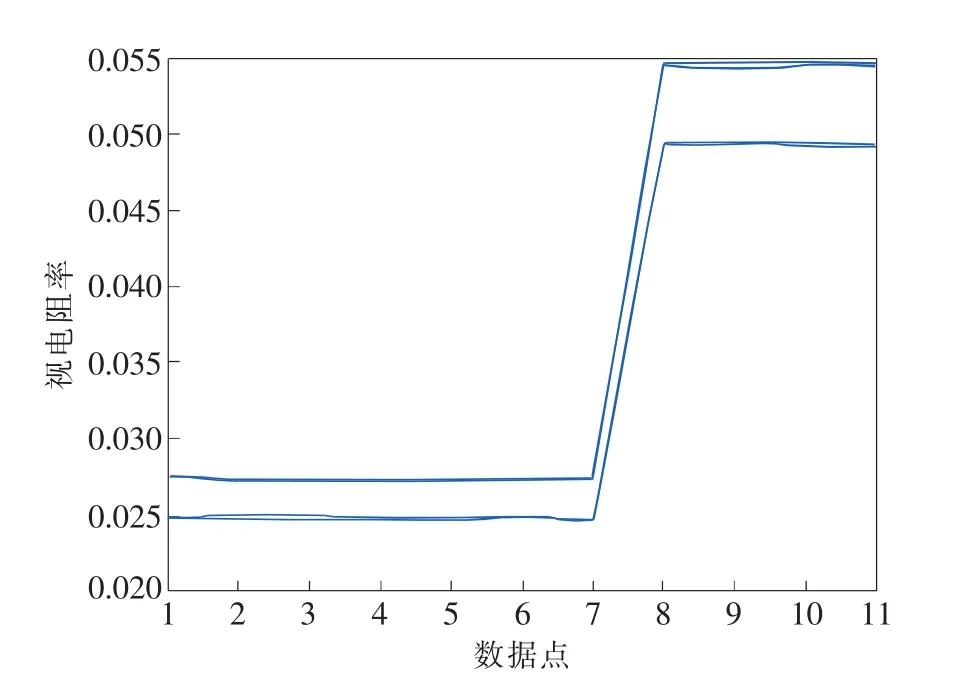
图5 各组视电阻率的数据点分布

3.2.1 一致性验证

动力锂电池内部状态ERT三维反演结果如图6所示，三幅图像描述了动力锂电池不同深度方向上每一层模型灵敏度的剖面分布图，从而构建起动力电池三维模型灵敏度分布。电池测区根据深度分为3个区域，这3个区域的模型灵敏度基本上是依次减少的（从区域1到区域3），这充分说明电流密度随深度增加而逐渐衰减。同时，浅层区域模型灵敏度分布更加均匀，说明动力电池表层电流强度大，电流密度能够均匀覆盖整个浅层区域。

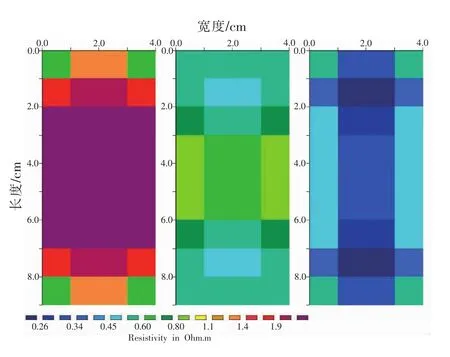
图6 动力电池的反演模型灵敏度分布

图7描述了动力电池在9次迭代后的内部视电阻率反演图像，不同色带值表征动力电池内部不同区域材料视电阻率值。可以看出动力电池在不同深度层上的色带值存在毛刺和断层，这些细节特征通常可以用来判断动力电池内部材料结构组成的变化趋势。对比图7（a）和图7（b），冰块组的视电阻率整体较低，符合视电阻率与温度的变化关系；图7（a）视电阻率整体呈中心对称分布，图7（b）标记处两侧分布不对称，因为右侧接近冰块，温度较左侧更低，因此相对应区域的视电阻率更低。反演结果与实际情况相符，能够很好地反映多次内部结构视电阻率分布变化趋势。图8左侧为动力电池内部视电阻率三维反演图像整体图，右侧为Y轴方向剖面图。

在实际评价体系中，反演误差RMS通常用来衡量最终成像效果，通过多次反演发现在进行10次迭代后反演平均均方误差RMS改变不明显，为3.34%。图9为测量视电阻率与计算视电阻率的反演误差RMS，整体上反演图像效果良好，说明视电阻率数据整体性能优良。

3.2.2 保真度验证

评价ERT反演图像的精度一般采用平均均方误差RMS，但是，具有最小RMS值的模型有时显示较大的、不实际的视电阻率值，因此具有最小RMS误差的模型并不一定是与实际情况最接近的模型，最保守的模型应该选择每次迭代后RMS的改变不明显的模型。为了检验光滑约束高斯-牛顿算法的成像质量，将光滑约束高斯-牛顿算法与常规高斯-牛顿迭代算法进行比较。以放置冰块的实验对象为测试模型。表1给出了光滑约束高斯-牛顿算法与常规高斯-牛顿迭代算法分别迭代5次、10次、20次图像反演结果，表2给出了两种反演算法的图像反演误差RMS。

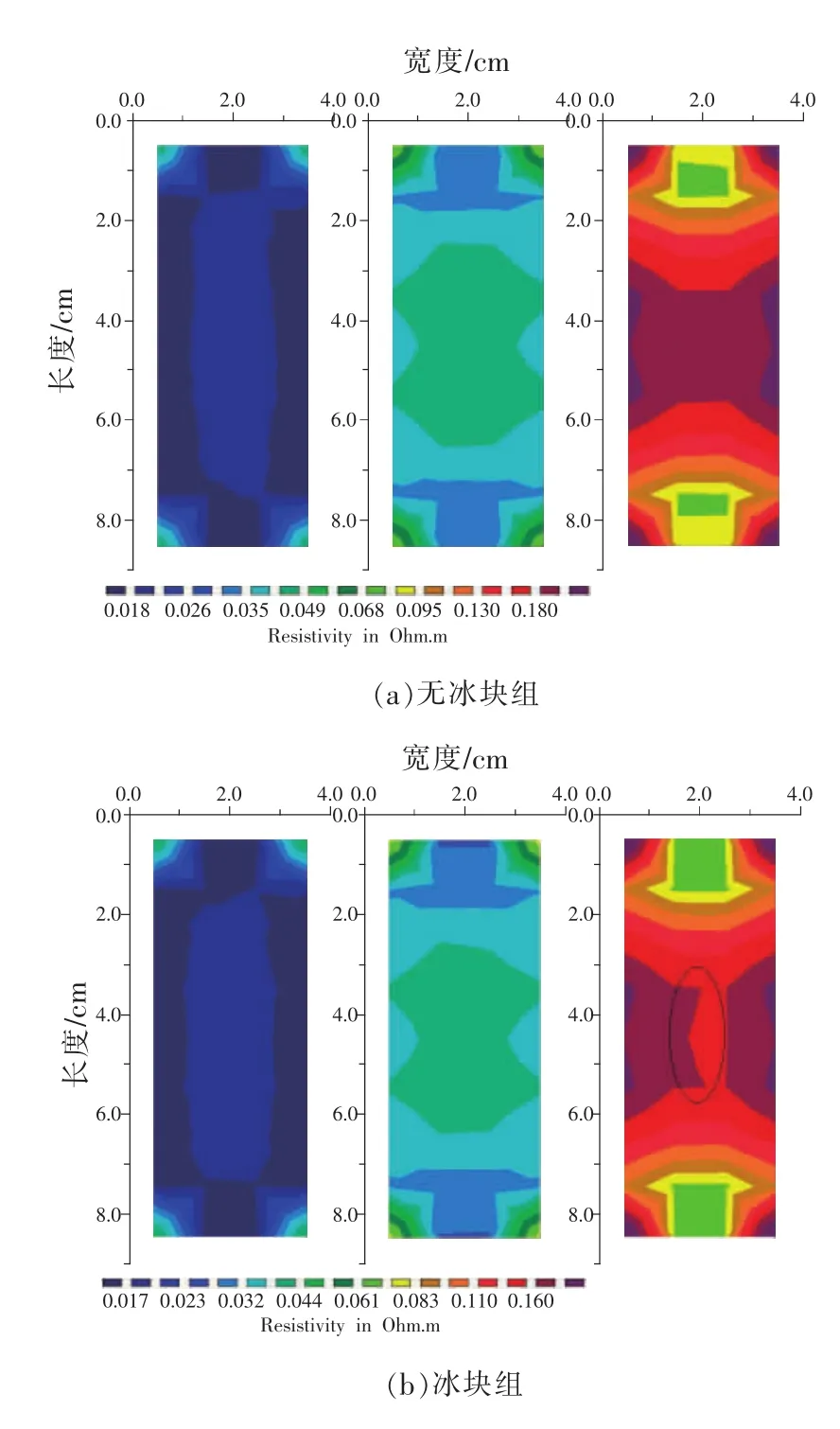
图7 动力电池内部视电阻率三维反演图像截面图

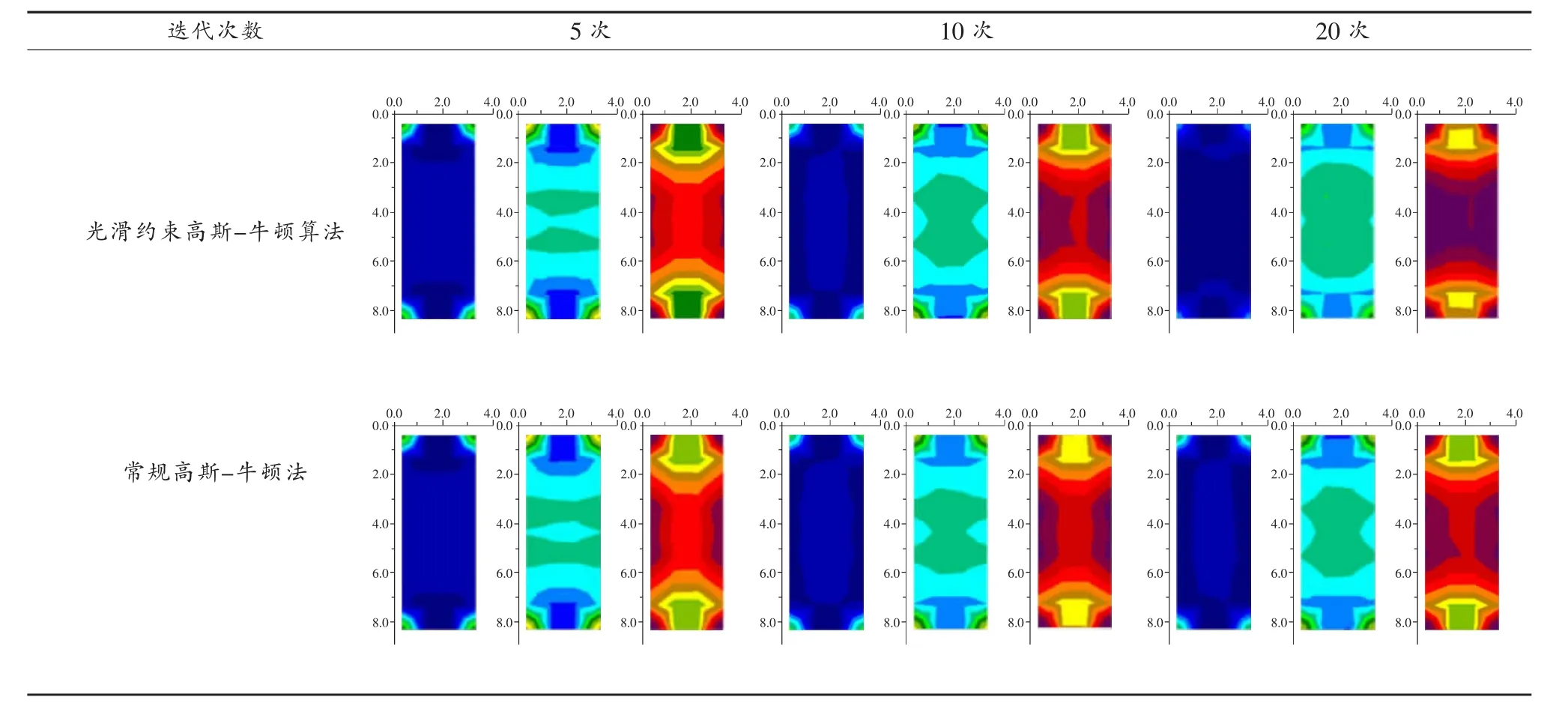
表1 两种算法反演图像比较

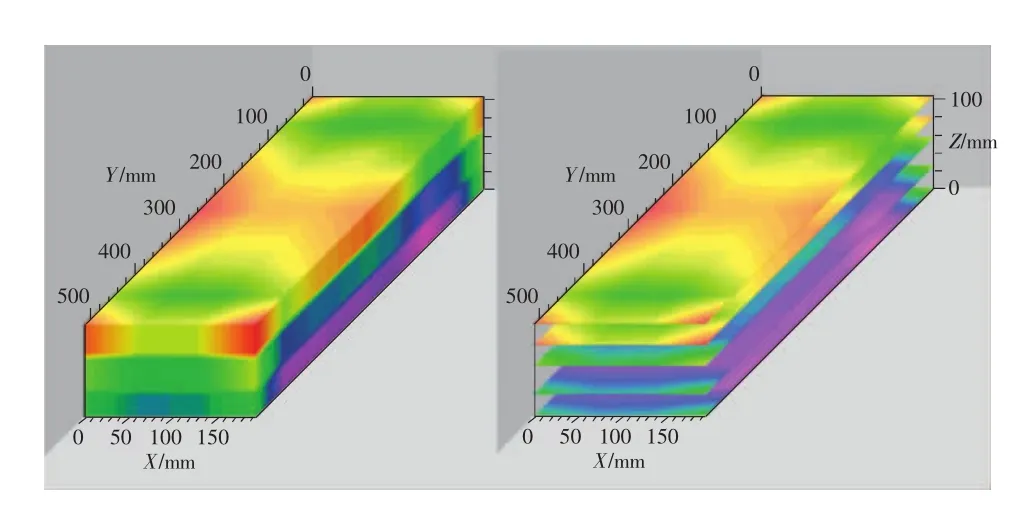
图8 动力电池内部视电阻率三维反演图像整体图

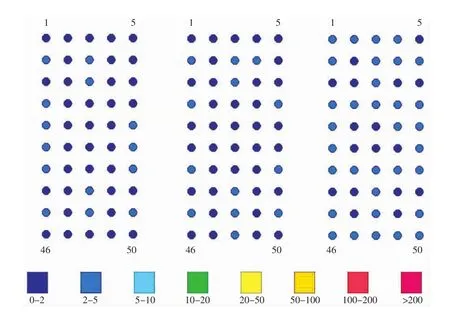
图9 测量视电阻率与计算视电阻率的反演误差RMS

表2 两种算法图像反演误差比较

可以看出，光滑约束高斯-牛顿算法质量优于常规高斯-牛顿法。光滑约束高斯-牛顿算法在迭代9次、10次左右的成像效果与常规高斯-牛顿法迭代20次的成像效果接近。从误差指标RMS看出，两种算法相同迭代次数下的RMS接近，光滑约束高斯-牛顿算法的RMS变化相对较稳定，标准差小。

电池的一致性和优越性是评价三维成像技术的一个重要手段。通过实验，说明该三维图像重建算法效果稳定，能够反映动力电池内部的视电阻率变化趋势，对动力电池内部的视电阻率分布做出有效评估，满足实际测量需求。

4 结束语

为了满足电阻层析成像图像重建算法应用于动力电池内部结构监测领域的精度与实时性要求，本文提出对标准高斯-牛顿算法施加光滑约束进行图像反演，使迭代步长在保证收敛的情况下达到最优化，这样就可以有效地提高成像的精度。结合实验对提出的光滑约束高斯-牛顿图像反演算法效果进行评估。实验结果表明，该三维图像反演算法效果稳定，10次迭代后反演误差RMS为3.34%，提高了检测效率，扩大了检测范围，能够反映动力电池内部的视电阻率变化趋势，对动力电池内部的视电阻率分布做出有效评估，满足实际测量需求。

[1]OH S H，KIM M，LEE J B.Influence of safety valve pressure on gelled electrolyte valve-regulated lead/acid batteries under deep cycling applications[J].Journal of Bulletin of the Korean Chemcal Society，2002，23（1）：75-80.

[2]MCCLEARY D A H，MEYERS JP，KIM B.Threedimensional modeling of electro-chemical performance and heat generation of spirally and prismatically wound lithium-ion batteries[J].Journal of the Electrochemical Society，2013，160（11）：1931-1943.

[3]于申军，周永超.内阻差异对锂离子电池组安全性能的影响[J].化工学报，2010，61（11）：2960-2964.

[4]TYAGI R C，MATHUR R S.Measurement of high temperature thermal conductivity of metals[J].Journal of Physics D：Applied Physics，1970（3）：1811-1815.

[5]NICK P，WILLIAM R B L.A matlabtoolkit for threedimensional electrical impedance tomography:A contribution to the electrical impedance and diffuse optical reconstruction software project[J].Meas Sci Technol，2002，13（12）：1871-1883.

[6]ZHDANOV M S，YOSHIOKA K.Cross-well electromagnetic imaging in three dimensions[J].Exploration Geophysics，2003，34（1-2）：34-40.

[7]DOETSCH J，LINDE N，VOGT T，et al.Imaging and quantifying salt-tracer transport in a riparian groundwater system by means of 3D ERT monitoring[J].Geophysics，2012（77）：207-218.

[8]徐光捷，杨献勇，陈鸥.电阻层析成像场域的三维仿真[J].清华大学学报，2005，45（2）：231-234.

[9]李守晓，王化祥.基于三维模型的改进正则化ERT成像算法[J].天津大学学报，2012，45（3）：215-220.

[10]洪晓斌，李年智，尹文伟.基于电阻层析成像的汽车动力电池内部温度监测[J].光学精密工程，2014，22（1）：193-203.

[11]洪晓斌，李年智，谢烁熳，等.动力电池内部视电阻率三维测量装置设计[J].中国测试，2015，41（1）：61-65.

（编辑：李刚）

Three-dimensional image reconstruction of apparent resistivity for power battery cell

XIE Shuoman，XU Weiying，HONG Xiaobin
（School of Mechanical Engineering，South China University of Technology，Guangzhou 510640，China）

Aiming to make image reconstruction algorithm for electrical resistance tomography（ERT）meet the acquirement of measurement for monitoring of internal structure of power battery in terms of precision and real-time，a newalgorithm for three-dimensional ERT image reconstruction is proposed.With the characteristics of the Gauss-Newton algorithm，the standard Gauss-Newton algorithm is applied to smooth constraint，which achieve the optimization of iteration step in the premise of ensuring convergence.The results showed that the algorithm of three-dimensional image with fast convergence and high accuracy improved the detection efficiency and expand the detection range；the algorithm can reflect the tendency of the apparent resistivity of the internal structure of power battery and estimate the distribution of the apparent resistivity of the internal structure of power battery，which meet the need of the measurement.

apparent resistivity；three-dimensional image reconstruction；Gauss-Newton algorithm；power battery

A

：1674-5124（2017）02-0119-06

10.11857/j.issn.1674-5124.2017.02.024

2016-06-20；

：2016-08-05

广东省科技计划项目（2016B010108001）；广州市科技计划项目（201607010171）；佛山市科技创新专项资金项目（2014HK100265、2016AG100255）

谢烁熳（1992-），女，广东揭阳市人，硕士研究生，专业方向为网络化测量与智能传感技术。

洪晓斌（1979-），男，广东揭阳市人，教授，博导，博士，主要从事无损检测技术与装备/网络化智能测控技术及应用研究工作。