面向瞬态EMI测试的FFT-SCZT算法研究

黄瑞龙，刘桂雄，黄 坚， 钟森鸣

（1.广东石油化工学院计算机与电子信息学院，广东 茂名 525000；2.华南理工大学机械与汽车工程学院，广东 广州 510641）

面向瞬态EMI测试的FFT-SCZT算法研究

黄瑞龙1，2，刘桂雄2，黄 坚2， 钟森鸣2

（1.广东石油化工学院计算机与电子信息学院，广东 茂名 525000；2.华南理工大学机械与汽车工程学院，广东 广州 510641）

针对传统接收机电磁干扰（electro-magnetic interference，EMI）测试实时性差，难以实现瞬态EMI信号测量的问题，提出基于快速傅里叶变换（fast Fourier transform，FFT）与分段线性调频Z变换（segmented chirp-Z transform，SCZT）结合的瞬态EMI测试方法。首先采用FFT对整个频谱进行初扫得到范围更小的特征频带；其次，基于SCZT时间复杂度低的特点，采用SCZT对特征频带进行频率细分；最后，应用FFT-SCZT测量对幅值动态变化、频率动态变化信号进行测量验证。实验结果表明：FFT-SCZT对幅值动态变化信号的频率、幅值测量相对误差分别小于0.0045%、2.4%，对频率动态变化信号的频率、幅值测量相对误差分别小于0.0047%、0.25%；FFT-SCZT算法可准确测量瞬态信号。

瞬态电磁干扰；快速傅里叶变换；线性调频Z变换；频率细分

0 引 言

电磁干扰的分析、预测与测试是电磁兼容领域的研究热点，准确、快速测量EMI信号频谱是当前关注的难点[1]。基于快速傅里叶变换、Z变换等离散时频变换算法实时性能满足瞬态EMI信号测量[2]，但对大频率跨度信号的高精度测量存在实时性瓶颈[3]。局部频率精细化技术是保证实时性实现频率分辨率提升的主要方法[4]，有细化FFT（zoom-FFT，ZFFT）、线性调频Z变换（chirp Z-transform，CZT）等。目前，Russer等[5]研究CZT测频误差，提出改进的正交平均CZT算法，改进算法的频率精度比传统CZT的精度提高约20倍；武汉光电国家实验室改进CZT频偏估计算法，改进算法与CZT算法精度相当，但硬件复杂度降低约75%[6]；南京理工大学结合矩阵特征分解与CZT的伪码序列盲估计算法，解决窄带干扰条件下含有未知载频直扩信号的伪码序列估计问题[7]；兰州交通大学采用ZFFT将信号频谱中感兴趣的局部频段进行精细化处理，实现低频移频信号准确测量[8]；文献[9]研究认为ZFFT和FFT点数是一致的，并不能真正提高物理分辨率实现频谱细化的功能；文献[10]提出一种FFT与CZT相结合的算法实现快速频谱分析，仅需2s即可实现107个数据点频谱分析。综上可知，FFT可实现大跨度频段快速频谱分析、SCZT可实现局部频率精细化的特点，若结合FFT和SCZT优势，将可实现准确、快速测量EMI信号频谱分析。

1 SCZT算法分析

1.1 SCZT算法

CZT变换可以对整个信号频带中的部分频带实现频率细分，同样的输入数据点，对受关注的频带，可获得比FFT变换高得多的频率分辨率。然而CZT变换运算复杂度过高，特别当数据量过大时，执行CZT算法需要大量的时间，不适合实时分析EMI信号频谱。为了改善CZT变换的执行效率及灵活地处理数据，需要对CZT算法进行改进。

欲分析的复频谱点数为M，设起始抽样点的矢量半径长度A0、起始抽样点相角ω0、相邻抽样点角度差ω1、螺旋线伸展率W0，则Z变换的抽样点zk为

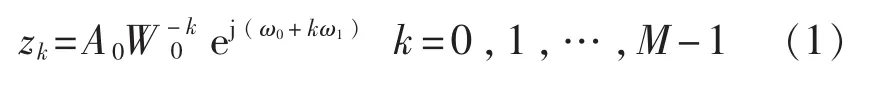
设采样数据序列为 x（n），则 x（n）的 Z变换Z{x（n）}为

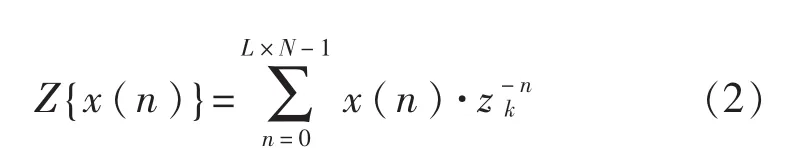
若将x（n）分为L段、每段长度为N，第i段数据xi（n）为

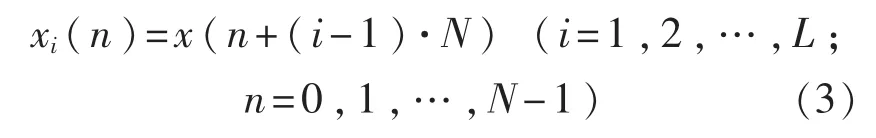
则式（2）可以化简为

用CZT{x（n）}表示x（n）的CZT变换，L段即有L次变换，其中M为任意正整数，可根据频率分辨率决定，则式（4）可表示为

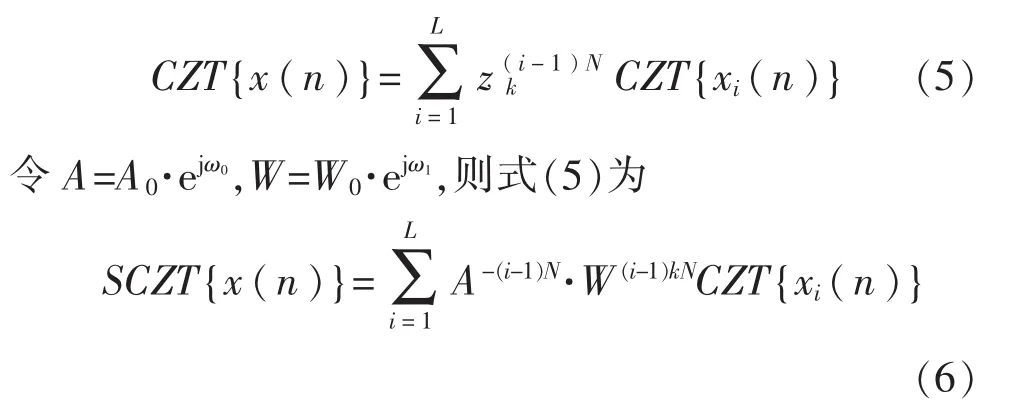
式（5）、式（6）的计算量比式（4）更小，计算效率更高。M可根据实际需要指定，对于需要频谱细分的频段[fstart，fend]，频率分辨率Δf为

可以看出SCZT算法具有分辨率、中心频段、带宽可定义的特点。

目前，Na2SO4水溶液研究较广泛，属于强电解质，可以在水溶液电解时起到提供Na+的作用进而提高电化学性能。然而Na2SO4水溶液电解液的研究还尚存在问题，比如：水溶液的工作电压较低、能量密度比较低、电化学窗口窄、氢氧析出副反应易泄漏等。因此发展其他的电解质体系，获得更优异的电化学性能是钠电池水溶液电解质的发展方向。

1.2 算法执行效率分析

由SCZT算法可知，SCZT算法和CZT算法执行结果理论上相同，但执行效率差别很大，输入长度为L×N的数据，X（zk）的长度为M时，FFT、CZT和SCZT算法执行的时间复杂度为

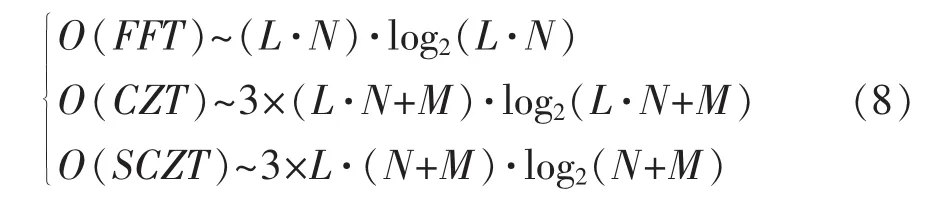
可以看出，SCZT的时间复杂度小于CZT时间复杂度，定义时间复杂度比值（TCR）为

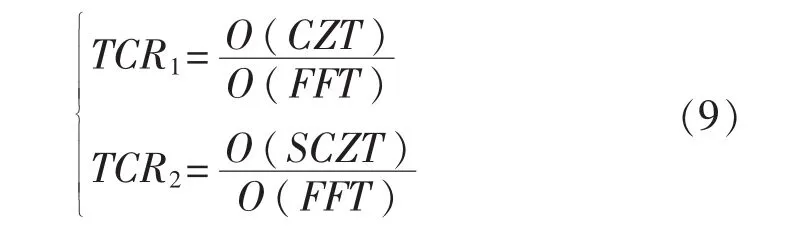
图1为FFT、CZT和SCZT之间的时间复杂度比值，图中选取参数 L（1～1 000），N=1 024，M=100、200、400和800。可以看出：1）相同M和N的条件下，分段数越多，SCZT相对于FFT的时间复杂度比值越小，而CZT变换时间复杂度约为FFT的3倍，没有明显改善。对于长数据块，分段越多，SCZT相对执行效率越高。2）相对于受关注的频段，分辨率要求越高，即M越大，SCZT的相对执行效率会越低，当受关注频率的分辨率提高800倍时，约为FFT执行时间的2.8倍（L=1000，N=1024）。3）就整个频段来说，不需要对每一个频率点都进行频率细分，只对部分频点进行细分时，SCZT变换效率会提高。

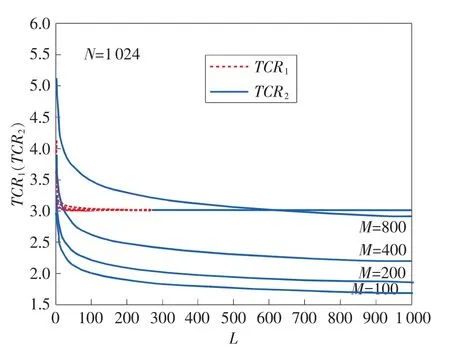
图1 FFT、CZT和SCZT之间的时间复杂度比值

2 FFT-SCZT算法的实现

在瞬态EMI测量中，为了快速测出EMI信号的峰值、准峰值或平均值，对采样数据连续应用FFTSCZT算法。FFT算法用来进行初扫，以确定需要频率细分的频段，SCZT算法用来对受关注的频段进行细分，以提高频率分辨率，具体过程为：

1）细分频带选择。对整个频带进行FFT变换初扫，确定需要细分的频带[fstart，fend]，记录超过5～10倍底噪水平或EMI测量标准限值的频率，图2为细分频带的带通滤波器，检测到EMI辐射水平超阈值的信号在滤波器4和滤波器5之间，则该频带就是需要进行频率细分的频带。设置滤波器为了减少频谱泄露，滤波器的带宽根据实际的应用可以适当调整，如在光频计反射域，滤波器的带宽可以设置为分辨率的20~100倍。

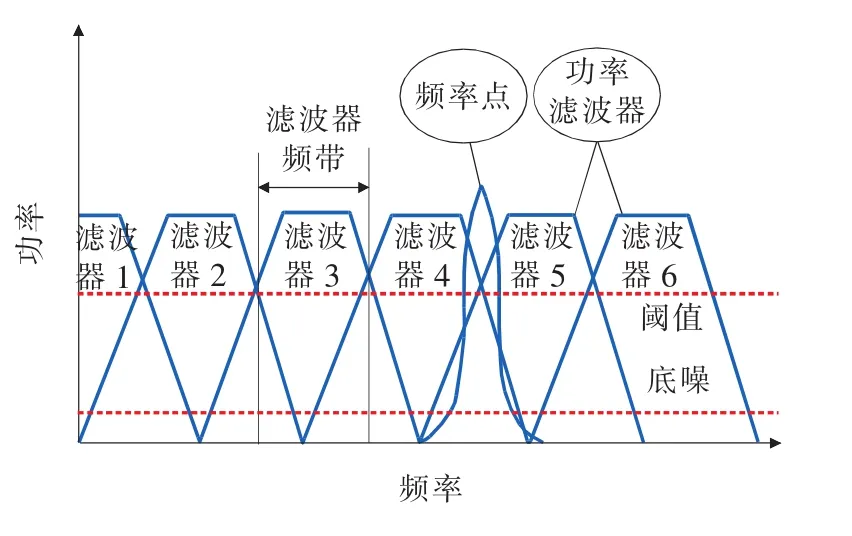
图2 细分频带的带通滤波器

2）选择窗函数。窗函数的频谱特性会影响实时FFT频谱分析精度，常用的窗函数有矩形窗、Hanning、 Flap Top、Gaussian等。窗函数选择时需注意频谱分析的实时性。

3 实验与验证

3.1 FFT、CZT和SCZT算法仿真分析

短时组合信号可以被SCZT算法独立采样，定义组合信号为

若令 A1_1=2 V，A1_2=1 V；f1_1=1 kHz，f1_2=2.5 kHz。采样频率fs=20kHz，采样数据Ns=32，并对仿真信号x1（t）分别进行FFT、CZT和SCZT变换（SCZT变换分为4段，每段8个数据）。图3为FFT、CZT和SCZT算法执行结果，图3（a）为原始信号曲线，图3（b）～（d）分别为FFT、CZT、SCZT变换得到的频率-幅值曲线。

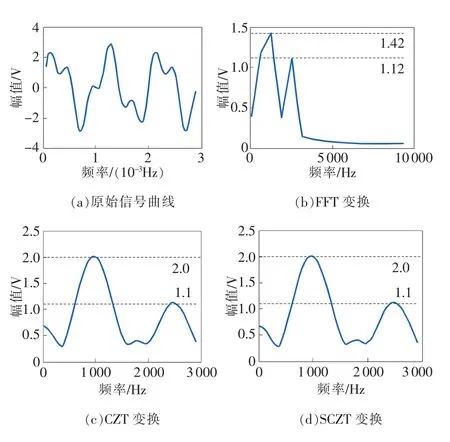
图3 FFT、CZT和SCZT算法执行结果

实际应用中可通过增加数据样点来提高测试分辨力，当Ns=512时，同样分为4段，每段128个数据，运算结果如图4所示。图中2个频率、电压点分别为（1 002，1.989 7）、（2 502，1.002），最大频率误差为2Hz，最大幅值相对误差δAmax=0.51%。

3.2 幅值动态变化信号仿真试验

SCZT算法可以侦测到幅值随时间变化的EMI信号，定义幅值变化的信号为

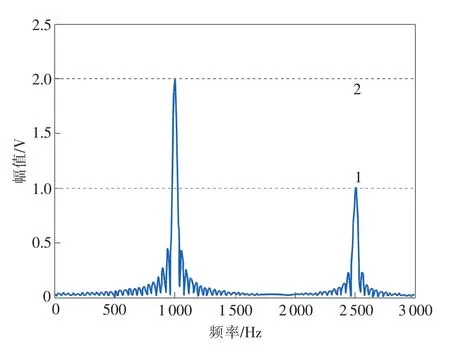
图4 SCZT频率细分结果

令 fs=200 MHz、A2=1.6 V、f2=25 MHz、Ns=4 096、BW=10MHz，图5为FFT、SCZT算法执行结果，图5（a）、图 5（b）分别为 x2（n）、x2′（n）经 FFT变换得到的频率-幅值曲线，图5（c）、图5（d）分别为x2（n）、x2′（n）经SCZT第1段得到的频率-幅值曲线。表1为不同频率幅值动态变化信号FFT、SCZT测量结果与误差分析。可以看出，SCZT的分段处理可以准确测量幅值动态变化信号，频率测量最大相对误差＜0.0045%，幅值测量最大相对误差＜2.4%。

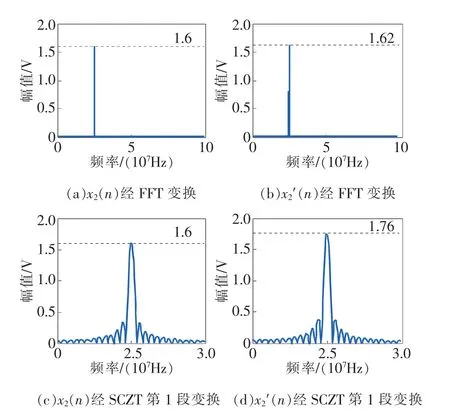
图5 动态幅值变化分析

3.3 频率动态变化信号仿真试验

定义频率随时间变化的瞬态EMI信号为

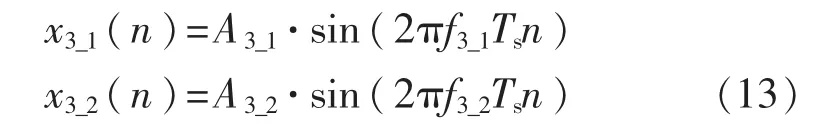
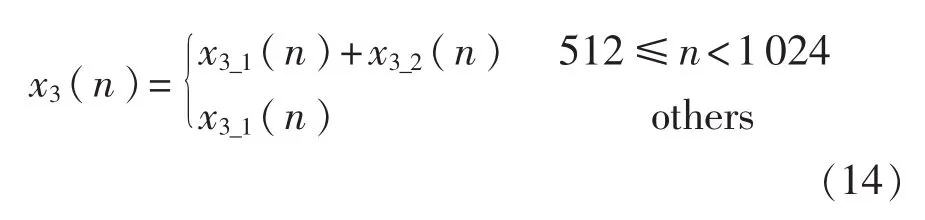
令A3_1=1.6V、A3_2=2.0V、f3_1=24MHz、f3_2=27MHz，Ts为采样时间。采样数据大小为4096，采样频率fs= 200MHz。图6（a）、图6（b）分别为x3（n）经FFT变换和SCZT变换的结果；图6（c）、图6（d）分别为x3（n）经SCZT第1段、第2段变换结果。表2为不同频率幅值动态变化信号FFT、SCZT测量结果与误差分

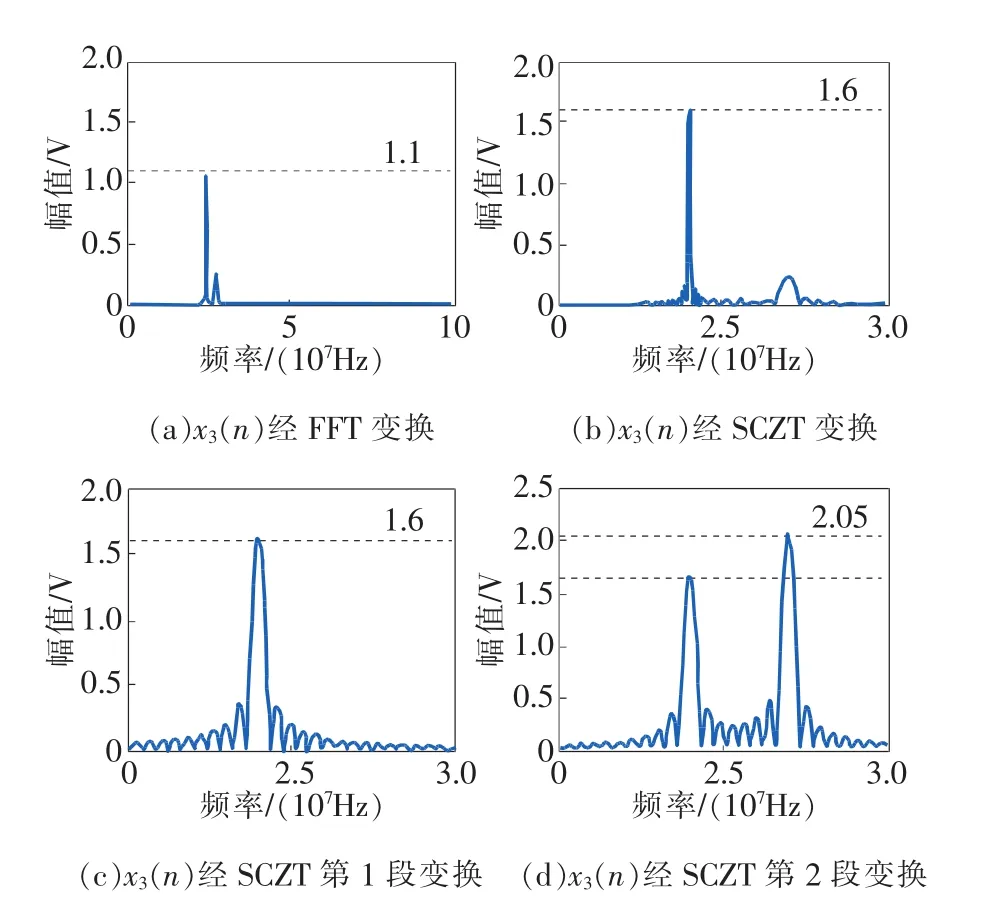
图6 动态频率变化分析

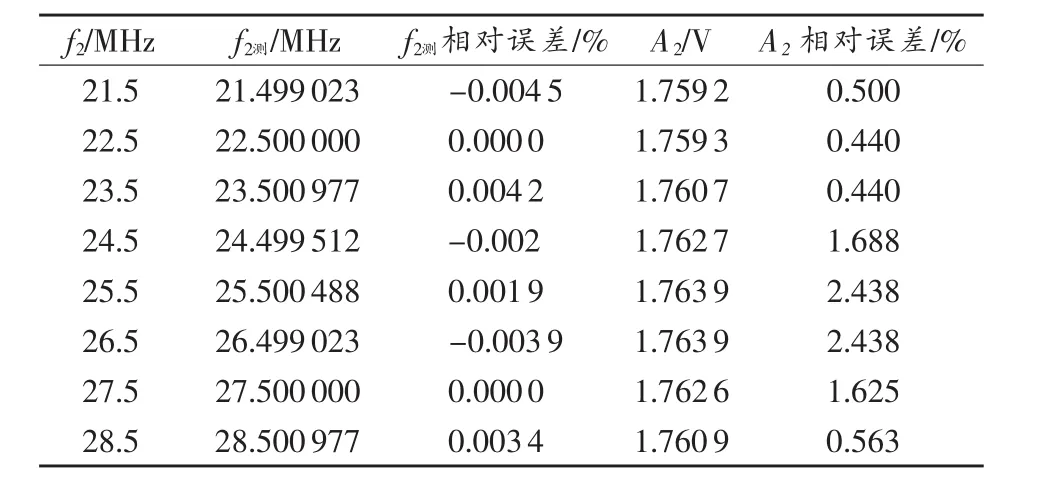
表1 幅值波动10%的瞬时EMI信号SCZT测量误差

表2 不同频率瞬时EMI信号SCZT估计误差

析。可以看出，SCZT的分段处理可以准确测量频率动态变化信号，频率测量最大相对误差＜0.0047%，幅值测量最大相对误差＜0.25%。

4 结束语

在瞬时EMI测量中，采用FFT-SCZT组合算法具有如下优点：

1）对EMI辐射较大的频谱，SCZT算法具有分辨率、中心频段、带宽可定义的特点，频率分辨力与实时性均优于FFT。

2）FFT对整个频带进行初扫，确定需要细分的频带，SCZT算法用来对受关注的频段进行细分，以提高频率分辨率。

3）FFT-SCZT组合算法可准确测量幅值动态变化、频率动态变化信号，幅值动态变化的频率、幅值测量相对误差分别小于0.0045%、2.4%，频率动态变化信号的频率、幅值测量相对误差分别小于0.0047%、0.25%。

[1]张润涵，扈罗全.基于稀疏表示的电力系统谐波信号频率分析[J].中国测试，2016，42（1）：35-37.

[2]ZHU L，ZHANG C.Fast fine acquisition algorithm of GPS receiver aided by INS information[J].Journal of Systems Engineering&Electronics，2011，22（2）：300-305.

[3]雷小亚，李贵子，朱琳，等.基于密集频谱校正的电流信号高准确度分离技术[J].中国测试，2015，41（12）：111-114.

[4]张媛，王楠.基于广义谐波小波的工频功率因数测量算法[J].中国测试，2016，42（1）：16-20.

[5]RUSSER J A，BRAUN S，FRECH A，et al.Time-domain measurementofspectra ofstochastic electromagnetic fields[C]∥International Conference on Electromagnetics in Advanced Applications，2013：1123-1126.

[6]冯婕，肖骏雄，韩纪龙，等.基于幅度比值的低复杂度频偏估计算法[J].光学学报，2015，35（5）：112-117.

[7]沈斌，王建新.窄带干扰条件下含有未知载频的直扩信号的伪码序列估计[J].电子与信息学报，2015，37（7）：1556-1561.

[8]李国庆，武晓春.基于复调制的ZFFT算法在轨道电路信号检测中的应用[J].计算机测量与控制，2016，24（1）：262-265.

[9]马可，张远安，张开生.CZT和ZFFT频谱细化性能分析及FPGA实现[J].计算机测量与控制，2016，24（2）：288-289.

[10]MA C，ZHOU Q，QIN J，et al.Fast Spectrum Analysis for an OFDR using the FFT and CZT Combination Approach[J].IEEE Photonics Technology Letters，2016（28）：1-1.

（编辑：李妮）

Research on FFT-SCZT algorithm for transient EMI measurement

HUANG Ruilong1，2，LIU Guixiong2，HUANG Jian2，ZHONG Senming2
（1.School of Computer&Electronic Information，Guangdong University of Petrochemical Technology，Maoming 525000，China；2.School of Mechanical&Automotive Engineering，South China University of Technology，Guangzhou 510641，China）

On account of bad real-time performance of electro-magnetic interference（EMI）receiver，transient signals EMI measurement was difficult to achieve.A fast Fourier transform（FFT）and segmented chirp-Z transform（SCZT）based transient signals EMI measurement method was proposed. The FFT was used in sweeping the whole frequency spectrum for locating the characteristic frequency spectrum.SCZT was applied to subdivide the characteristic frequency spectrum，according to the low time complexity of it.FFT-SCZT was used in measuring simulation transient EMI signals. The results show that measured by FFT-SCZT algorithm，for amplitude transient signals，the relative error of frequency and amplitude were less than 0.004 5% and 2.4% respectively.For frequency transient signals，the relative error of frequency and amplitude were less than 0.004 7% and 0.25%.

transient EMI；FFT；CZT；frequency subdivision

A

：1674-5124（2017）02-0109-04

10.11857/j.issn.1674-5124.2017.02.022

2016-07-01；

：2016-08-15

广州市科技计划项目（201504010037）

黄瑞龙（1977-），男，广东茂名市人，讲师，硕士，主要从事智能传感技术及电磁兼容检测方面研究。