平方根球形无味卡尔曼滤波机载无源定位算法

裴 畔， 丁永红， 马铁华

（1.中北大学 仪器科学与动态测试教育部重点实验室，山西 太原 030051；2.中北大学 电子测试技术国家重点实验室，山西 太原 030051）

平方根球形无味卡尔曼滤波机载无源定位算法

裴 畔1，2， 丁永红1，2， 马铁华1，2

（1.中北大学 仪器科学与动态测试教育部重点实验室，山西 太原 030051；2.中北大学 电子测试技术国家重点实验室，山西 太原 030051）

针对机载无源定位系统中，初始值误差和数值的舍入计算对无味卡尔曼滤波（un-scented Kalman filtering，UKF）算法的定位精度和滤波稳定性影响较大的问题，提出一种基于平方根球形无味的卡尔曼滤波算法（square root spherical unscented Kalman filter，Sqrt-UKFST）。该方法以单位超球体球面无味变换为基础，通过减少采样点数目和球面半径，保证所有采样点在一个单位超球体上，从而提高算法对初始值的鲁棒性，并采用平方根滤波提高算法的数值稳定性。对该算法进行100次Monte-Carlo实验，仿真结果表明，Sqrt-UKFST算法收敛速度快，滤波性能稳定；当初始状态估计误差较大时，Sqrt-UKFST算法的定位精度保持在30%以内，提高系统对初始值的鲁棒性。

机载无源定位；算法精度；平方根球形无味卡尔曼滤波；球面无味变换；鲁棒性；稳定性

0 引 言

在电子对抗日趋激烈的今天，机载单站无源定位系统自身不发射信号，只接收辐射源目标发射的电磁波信号，具有隐蔽性能好、生存力强、设备简单、跟踪定位性能好的优点，在对地面静止目标或慢速运动的目标定位上具有重要的应用价值[1]；文献[2]基于多普勒变化率实现对固定目标的定位；文献[3]利用相位差变化率对地面固定目标进行定位；文献[4]基于相位差变化率和多普勒变化率相结合的定位方法将多普勒频率变化率法观测参数中的角度变化率由相位差变化率法中的相位差变化率参数替换，提高算法的实时性和实用性。机载无源定位是一个典型的非线性滤波问题，对含有噪声的数据进行观测，从而估计目标的状态。为了提高系统的定位精度和稳定性能，需要研究跟踪滤波算法，对观测信息进行最大限度的利用。

文献[5]采用修正EFPF算法进行滤波，标准的无味卡尔曼滤波（unscented Kalman filter，UKF）算法在扩展卡尔曼滤波（extended Kalman filter，EKF）算法的基础上，摒弃了线性化近似模型的做法，将随机变量的概率分布进行近似，利用比例修正的对称采样策略，对一个n维状分布态空间，选取2n+1个采样点，提高了定位精度，不用计算雅克比矩阵，降低了算法的复杂度[6-7]。文献[8]和文献[9]采用改进的UKF算法提高系统的滤波性能。基于施密特正交变换（schmidt orthogonal transform，SOT）采样策略的UKF（SOUKF）算法，经过施密特正交变换后确定n+1个采样点，减少了UKF算法所需采样点的数目，提高了计算效率[10]。文献[11]采用的平方根UKF双向滤波算法，提高了滤波性能，但计算比较复杂。本文提出了一种平方根球形无味卡尔曼滤波（square root spherical unscented Kalman filter，Sqrt-UKFST）算法，提高实时性的同时，采用单位超球体球面无味变换的采样策略，在滤波算法递推过程中采用平方根滤波的方法，提高了算法的数值稳定性及对初始值的鲁棒性。

1 机载无源定位系统模型

以二维平面直角坐标系为例（见图1），假设飞机在k时刻的位置坐标为（xOk，yOk），速度为（目标辐射源在k时刻的位置坐标为（xTk，yTk），速度为飞机O和目标辐射源T在k时刻的状态向量分别为

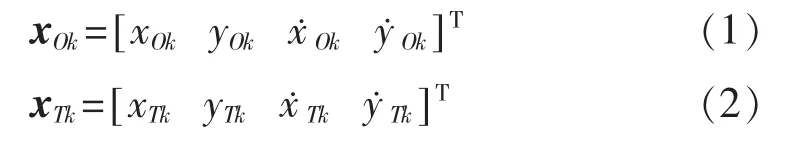
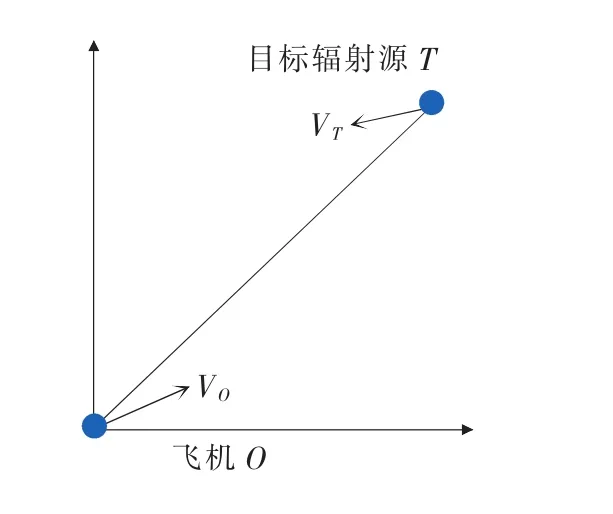
图1 飞机对目标辐射源定位的二维示意图

1.1 系统的状态方程

假设飞机做匀速直线运动，忽略加速度项。目标辐射源相对于飞机是匀速运动，相对运动状态向量是

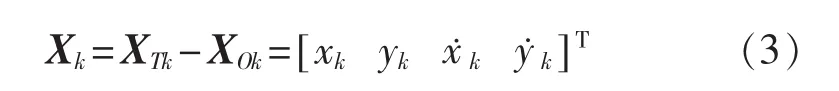
系统的状态方程表示为

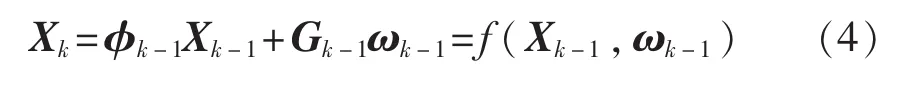
其中，xk和yk表示k时刻目标的位置变量，x˙k和y˙k表示k时刻目标的速度变量。表示状态转移矩阵，T表示测量周期，I2表示二阶单位矩阵；是噪声转移矩阵[10]，状态噪声是二维零均值高斯白噪声，其协方差矩阵是Qk。

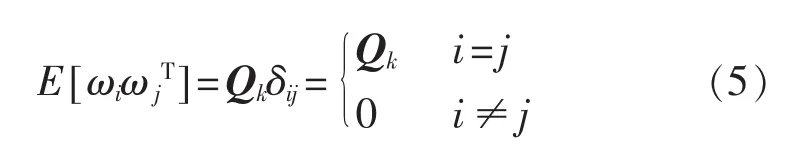
1.2 系统的观测方程

本文采用多普勒变化率的机载无源定位方法，只需要测量方位角、方位角变化率以及目标相对于飞机的多普勒变化率。系统的观测方程表示为

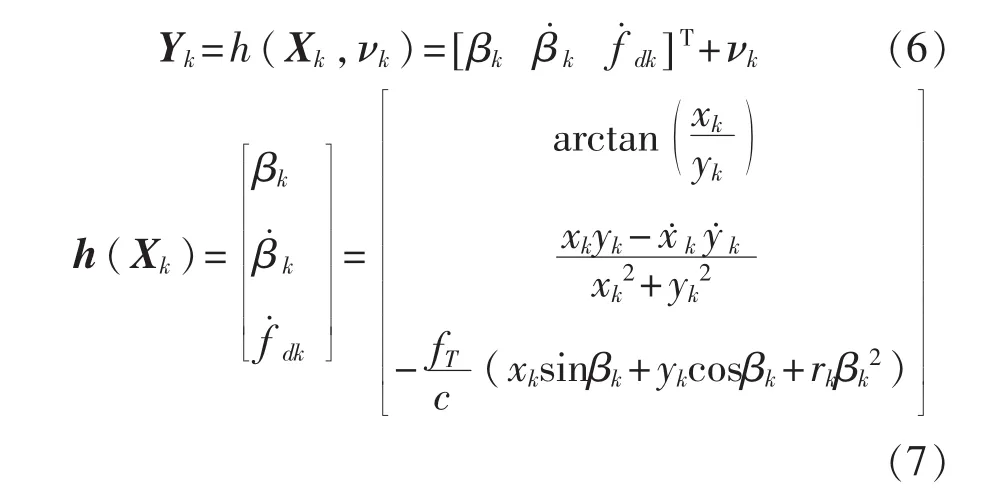
其中，fT表示目标辐射源辐射的频率，c表示电磁波传播速度表示飞机距离目标之间的相对距离，h（Xk，νk）是从状态向量向观测向量转化的非线性函数，量测噪声是零均值高斯白噪声，其协方差矩阵是

2 Sqrt-UKFST算法

2.1 单位超球体球面无味变换

UKF算法的计算成本与采样点σ的数量成正比，有必要减少σ点。目前σ点的采样策略有：无味、单纯形和球形变换。假设系统的维度是n，无味变换需要2n+1个σ点；单纯形变换需要n+1个σ点，它的数值稳定性与球体半径2n/2有关[12-13]。本文提出的球形变换需要n+2个σ点，通过减少球面半径至提高系统的数值稳定性。

其中，初始权重W0只影响选择的四阶及高阶的σ点。球面半径上的σ点分布取决于估计状态向量的大小，保证所有σ点在一个单位超球体上。单位超球体球面无味变换步骤如下：

1）选择初始权重0≤W0≤1。

2）计算权重的其余部分

其中，Wi表示均值和协方差加权的权值，i=1，2，…，n+1。

3）元素向量初始化

4）递推扩展后（j=2，…，n），迭代公式如下：

2.2 平方根无味卡尔曼滤波器

对于标准的UKF算法，协方差矩阵Pk是通过公式Pk=SkSTk更新和分解到矩阵广根Sk，σ点映射在每个时间步。然后，Pk矩阵重构来传播更新σ点。Sqrt-UKFST算法直接传播和更新Sk，没有分解和重构矩阵Pk的需要，节省了重构Pk在每步的时间。平方根UKF算法利用3种方法更新和传播：QR分解、乔里斯基因素更新（cholupdate）和最小二乘法[14]。Sqrt-UKFST算法步骤如下：

1）设置初始状态均值和协方差

其中，chol表示cholesky分解。

2）计算σ点的预测值，i=0，1，…，n+1

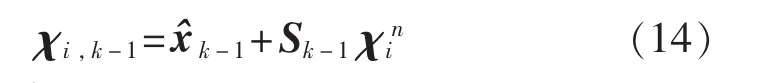
3）状态估计预测

4）估计状态均值

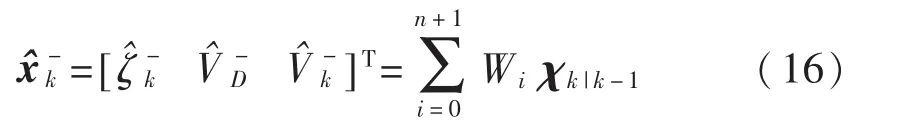
5）协方差平方根递推和更新

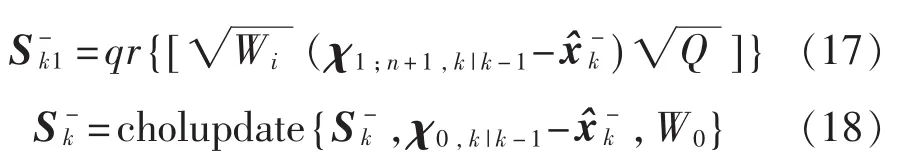
6）估计测量rk和均值

7）计算协方差测量Sy¯k1和它的更新值

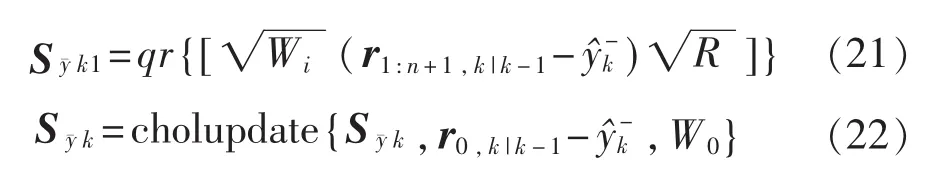
8）计算交叉协方差矩阵

9）卡尔曼增益Kk和状态估计更新

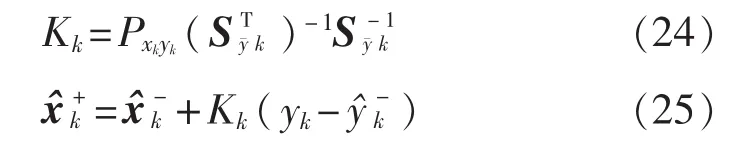
10）更新协方差矩阵

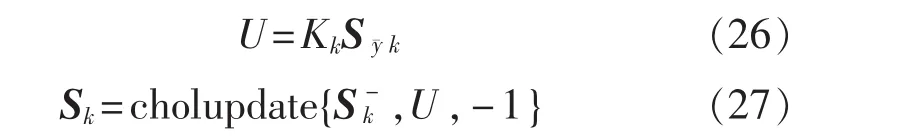
3 仿真条件与结果分析

假设飞机起始点在坐标原点，作水平匀速直线运动且忽略姿态变化，速度为vx=vy=300m/s。飞机对平面上运动的目标辐射源进行观测，目标的起始位置为 x0=2 km，y0=10 km，速度为 vx=vy=－15 m/s，加速度扰动噪声的协方差矩阵为Q=0.001I2×2。对x方向和y方向分别进行观测，观测周期 1 s，持续时间100s，测量精度为σβ=3mrad，σfd=1Hz，σβ′=0.1mrad/s，σfd′=0.5Hz/s。

滤波误差的均值用来描述算法的稳定性能，计算公式[14]为

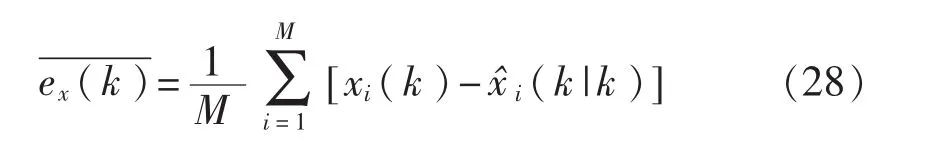
式中：M——蒙特卡洛模拟次数；

N——采样次数，k=1，2，…，N。

图2 X方向和Y方向的估计误差均值

图3 RRE的统计平均值

表1 不同算法的单次运行时间

相对距离误差（relative range error，RRE）用来评估算法的收敛性能。RRE的计算公式[15-16]为

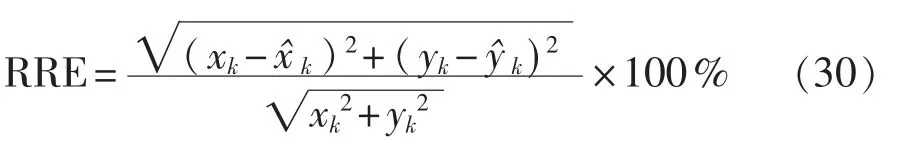
其中（xk，yk）和分别表示目标在k时刻的真实位置和估计位置。

为了验证算法的稳定性，收敛性和定位精度，对UKF、SOUKF和Sqrt-UKFST 3种算法分别进行100次Monte-Carlo实验，得到滤波误差在两个方向上的均值曲线和RRE的统计平均值。分别如图2、图3和表1所示。

由图2可以看出，Sqrt-UKFST算法比UKF算法和SOUKF算法的滤波性能都更稳定，曲线波动更小。

由图3可以看出，在相同的观测精度下，Sqrt-UKFST算法的定位精度最好且收敛速度最快，SOUKF算法次之，UKF算法最差。忽略曲线中个别发散点，若RRE<15%，则实验结果收敛，否则发散。

由表1可以看出，Sqrt-UKFST算法和SOUKF算法的运算时间比UKF算法短，Sqrt-UKFST算法运算时间比SOUKF算法略多，仍然可以满足实时性要求。

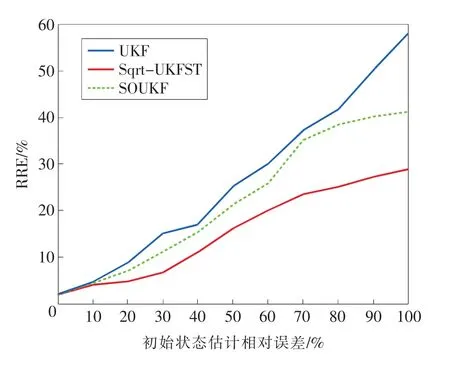
图4 初始状态估计相对误差变化时3种算法定位精度曲线

表2 初始状态估计相对误差变化时3种算法定位精度 %

为了检验Sqrt-UKFST算法对初始值的鲁棒性，初始状态估计相对误差取从0到100%的11组值。在不同的初始状态估计相对误差下，作100次Monte-Carlo实验，将RRE的统计平均值作为算法的定位精度，仿真结果如表2和图4所示。

由表2可以看出，在初始状态估计误差较低时，3种算法的定位精度都保持在15%以内，收敛性良好。当初始状态估计误差较大时，Sqrt-UKFST算法的定位精度保持在30%以内，UKF算法的定位精度达58.1%。

由图4可以看出，UKF算法的变化程度最大，说明该算法对初始值估计相对误差最敏感，而Sqrt-UKFST算法的变化程度最小，说明该算法对初始值的鲁棒性最好。

4 结束语

本文在采用角度、角度变化率和多普勒变化率的机载无源定位方法的基础上，提出了一种基于平方根球形无味的卡尔曼滤波算法（Sqrt-UKFST）。该算法以单位超球体球面无味变换为采样策略，在满足实时性要求的条件下，保证所有采样点在一个单位超球体上，提高算法对初始值的鲁棒性。同时，在滤波算法递推过程中采用平方根滤波的方法，提高了滤波的稳定性和收敛性。仿真结果也表明，Sqrt-UKFST算法比UKF算法和SOUKF算法具有更好的跟踪性能，对机载无源定位系统具有重要的应用价值。

[1]刘学.机载无源定位技术与跟踪算法研究[D].哈尔滨：哈尔滨工程大学，2012.

[2]平殿发，司文健，苏峰.基于多普勒变化率的机载无源定位方法研究[J].中国雷达，2010，29（4）：4-6.

[3]侯建民.基于相位差变化率的空中运动单站对地面固定目标的无源定位[D].合肥：合肥工业大学，2015.

[4]张志.机载单站无源定位关键技术研究[D].南京：南京理工大学，2013.

[5]申正义，闫抒升，王晓军，等.修正的EKPF算法在固定单站被动目标跟踪中的应用[J].现代防御技术，2015（2）：116-121，153.

[6]黄耀光，李建新，高博.基于UKF的单站无源定位改进算法[J].现代雷达，2012，34（11）：45-48.

[7]QIU L B，SU H Y，HAO H，et al.Application of UKF algorithm in airborne single observer passive location[J]. Advanced Materials Research，2011（267）：356-362.

[8]AI-HUSSEIN A，HALDAR A.Unscented Kalman filter with unknown input and weighted global iteration for health assessment of large structural systems[J].Structural Control and Health Monitoring，2016，23（1）：156-175.

[9]ZHAO H S，WEN Z Y，YU H P.A new method of multi-sensor data fusion based on multiscale analysis and UKF[J].Internatonal Journal of Control and Automation，2016，9（2）：329-342.

[10]黄耀光，高博，李建新，等.基于施密特正交变换UKF的单站无源定位算法[J].电光与控制，2013，20（02）：37-40.

[11]黄耀光，高博，李建新，等.基于平方根UKF双向滤波的单站无源定位算法[J].数据采集与处理，2013，28（02）：207-212.

[12]ZHAO K C，YOU Z.Square root spherical simplex unscented kalman filter for micro satellite attitude measurement[A].2nd International Conference on Information Engineering and Computer Science-Proceedings(ICIECS2010)[C]∥2nd International Conference on Information Engineering and Computer Science-Proceedings. ICIECS，2010.

[13]HTET A，KAY S L，SHU T G.State-of-charge estimation of lithiumion battery using square root spherical unscented kalman filter（Sqrt-UKFST）in nanosatellite[J]. IEEE Journals&Magazines，2015，30（9）：4774-4783.

[14]LI W X，HUANG C Q，WANG Y，et al.An improved airborne passive location&tracking algorithm using the rate-of-change ofphase difference[J].Journal of Electronics and Information Technology，2013，35（1）：68-73.

[15]万某峰，赵长胜.UKF滤波中蒙特卡洛采样策略比较分析[J].测绘通报，2012（12）：37-39.

[16]黄小平，王岩.卡尔曼滤波原理及应用：Matlab仿真[M].北京：电子工业出版社，2015：71-79.

（编辑：刘杨）

Airborne passive location algorithm based on spherical square root unscented Kalman filter

PEI Pan1，2，DING Yonghong1，2，MA Tiehua1，2
（1.Key Lab of Instrumentation Science&Dynamic Measurement，North University of China，Taiyuan 030051，China；2.Key Laboratory of Electronic Measurement Technology，North University of China，Taiyuan 030051，China）

As the unscented Kalman filtering（UKF）in airborne passive location has greater impact on positioning accuracy and stability because of the initial value and numerical calculation error，an improved smoothing algorithm based on square root spherical unscented Kalman filter（Sqrt-UKFST）is presented.To guarantee that all sampling points on a unit hypersphere algorithm to improve the robustness of the initial value，the algorithm uses the unit hypersphere sphere tasteless converted by reducing the number of sampling points and the spherical radius.And the algorithm utilizes the square root matrix in the process of estimation to improve the stability of the filter. After 100 times Monte-Carlo experiments，simulation results show that the Sqrt-UKFST algorithm has better performance in the filter’s stability，convergence velocity and the robustness of the initial value.When the initial state estimation reaches big error，the positioning precision maintained less than 30%.

airborne passive location； algorithm accuracy； Sqrt-UKFST； sphericaltasteless transformation；robustness；stability

A

：1674-5124（2017）02-0093-05

10.11857/j.issn.1674-5124.2017.02.019

2016-06-06；

：2016-08-07

国家自然科学基金项目（61471385）

裴 畔（1991-），女，山西临汾市人，硕士研究生，专业方向为机载无源定位。