产品表面检测的变步长采样机制研究
郭 静,韩跃平,贾志前,李会鸽
(中北大学信息与通信工程学院,山西 太原 030051)
产品表面检测的变步长采样机制研究
郭 静,韩跃平,贾志前,李会鸽
(中北大学信息与通信工程学院,山西 太原 030051)
针对产品表面缺陷检测系统中,由于定步长数据采集造成数据冗余量大、工作效率低的现象,提出变步长自适应的数据采集方式,以信号变化为采样依据实现调频。首先,基于采样步长的影响因素(乃奎斯特采样定理、识别尺寸、弧度畸变及空间畸变),推导出采样步长的函数关系表达式。其次,采用Matlab仿真平台,利用最小二乘法拟合,具体分析并验证被检产品各待检区域通过公式计算得到的采样步长均在95%的置信区间内。实验表明:推导出的采样步长公式为产品各待检区域旋转步长的合理选取提供理论依据;该模式可以根据不同信号实现频率自适应调节,可提高获取信息的利用率并减少数据冗余。
数据采集;变步长采样;数据拟合;表面缺陷
0 引 言
随着生活生产的发展和社会科技的进步,人类对产品的质量要求也在逐渐提高,产品表面缺陷检测是一种重要的质量控制手段,是机器视觉检测的一个重要领域,已广泛应用于工业生产中的各个方面[1]。然而目前,大部分产品表面检测系统的数据采集过程,均采用固定旋转步长[2-3]进行采样,单一的定步长无法满足自适应的需要,无法对产品表面不同待检区域实现最优检测。定步长采样即等间隔的采样方式,容易造成大量的冗余数据堆积,导致后续信息传输、存储的复杂度大,工作效率低。
针对定步长采样的弊端,本文提出了变步长自适应的数据采集方式,即根据产品各待检区域信号变化为采样依据实现调频。该方法可以根据不同信号实现频率自适应调节,保证采集精度并能够去除冗余数据[4-6]。
1 采样步长的影响因素分析
1.1 乃奎斯特采样定理
乃奎斯特采样定理[7]对具有最高频率fc的连续信号x(t)进行离散采样时,若要采样后的数字信号x(nTs)可以完整地拥有原始信号中的信息,则必须使采样频率fs满足以下条件:

根据上述定理,对随机放置的被检产品进行采样,如果被检产品的最小目标尺寸为d,则它与之对应的最大空间频率是1/d,故获得被检产品数字图像的分辨率必须≥2/d,否则该数字图像就会丢掉原来产品中有用的信息量,即对尺寸为d的最小区域无法进行识别。若被检测产品旋转采集的两幅图像之间丢失1个像素单元时,其刚好转过2°,则对尺寸大小为1mm的待检区域采样步长必须≤2°。否则,被检产品数字图像会丢失其周向方位信息,无法准确识别被检产品[8-9]。
1.2 空间几何关系对采样步长的影响
选取表面具有黑色长条图案的轴回转体进行研究,如图1所示,圆柱体的底圆半径表示待检区域的弧度畸变r(即待检区域到旋转轴线的距离),黑色长条表示待检区域识别尺寸d,其水平投影尺寸为d′,黑色长条与水平方向的夹角表示待检区域的空间畸变α。
如图2所示,点A、B为CCD相机视角可观察到圆柱体表面的边缘点(弧长CB等于弧长BD),BD表示d在俯视图中的水平投影尺寸d′,β表示待检区域从弧CB位置旋转到弧BD位置时旋转的角度。
经多次实验数据分析得出:产品最大采样步长同时受限于d、r与α。
其中,由图2的几何关系可得:

整理得:


图1 实验对象
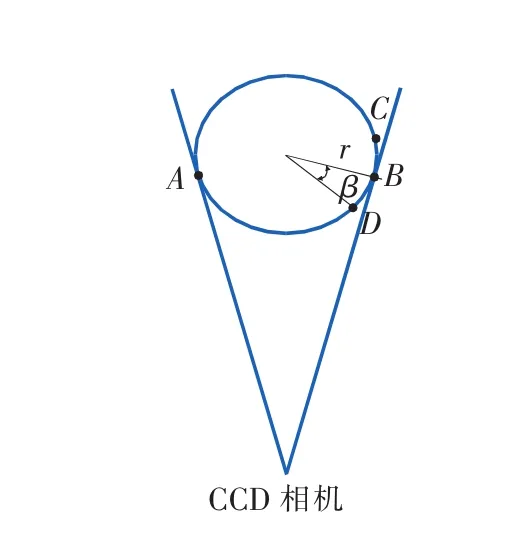
图2 CCD相机图像采集俯视图
由图1(c)的几何关系可得:

综上所述:
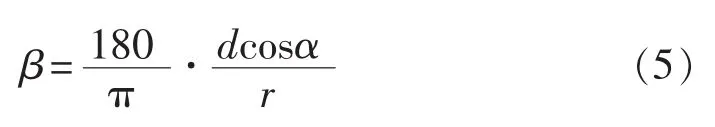
故待检区域的最大采样步长θ为
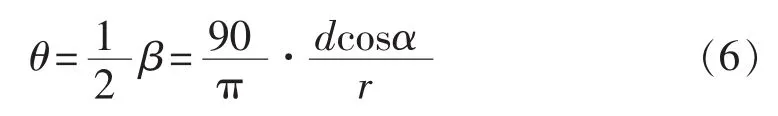
由式(6)可知,理论上待检区域的采样步长θ随最小识别尺寸d、弧度畸变r及其空间畸变α的变化而变化。
2 实验结果与分析
实验环境为:Intel(R)Core(TM)i5-2450M CPU@ 2.5GHz处理器,Windows7操作系统,Matlab仿真平台,奥林巴斯FE4010相机。
通过使用垂直投影法[10-11]来获取被检区域旋转角度β。例如,针对如图3(a)所示的待检区域,其垂直投影图如图3(b)所示。经多次实验分析得出,在垂直投影图中当相邻冲击波峰(波谷)距离≥20pixels时,会显示完整图像,而此时对应的旋转步长为20°,即被检区域旋转角度β为20°。
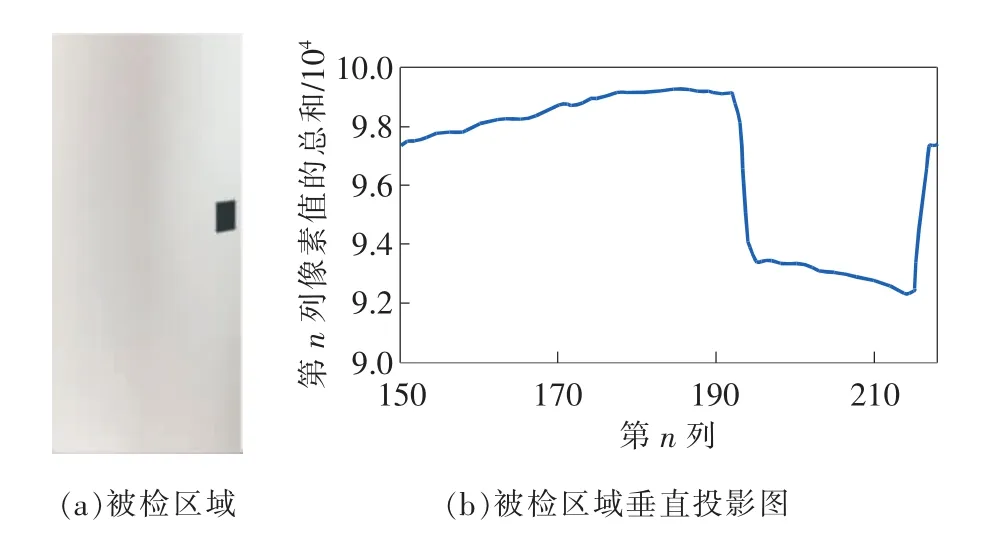
图3 被检区域旋转角度获取过程
2.1 验证被检区域旋转角度β与最小识别尺寸d的关系
由式(5)可得:
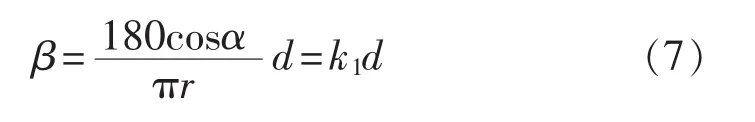
当α,r取值不变时,k1为常数,则β是d的正比例函数。为验证上述算法的效果,如图4所示,选取当α=0°且r=16mm时表面具有不同最小识别尺寸d的黑色长条图案的圆柱体进行实验。通过垂直投影法获取各被检区域的旋转角度β,其取值如表1所示。

图4 不同识别尺寸的待检产品

表1 被检区域识别尺寸d与旋转角度β的取值
采用最小二乘法[12-14]对实验获取的数据做二维拟合,得到被检区域的旋转角度与被检区域最小识别尺寸的拟合曲线如图5所示,其拟合公式为

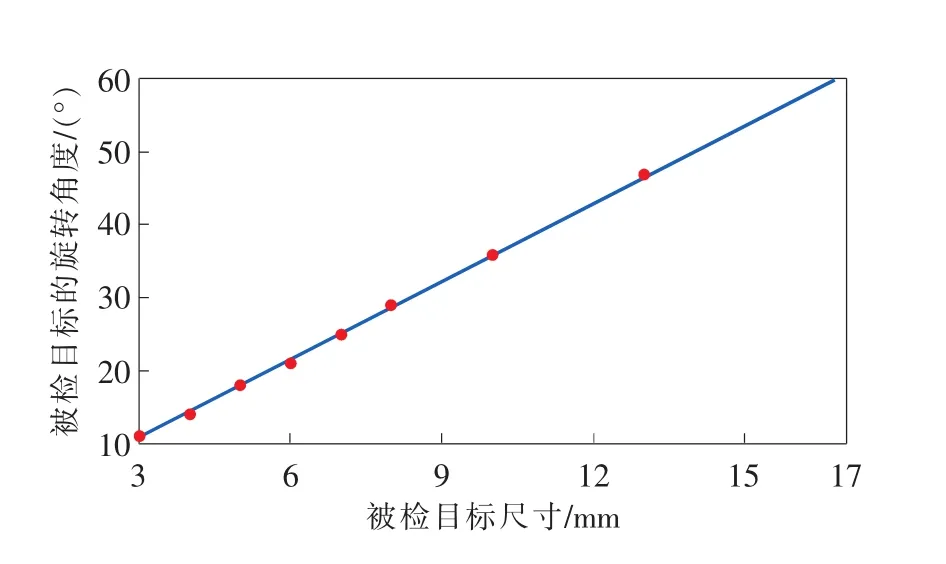
图5 被检区域的旋转角度与最小识别尺寸的拟合
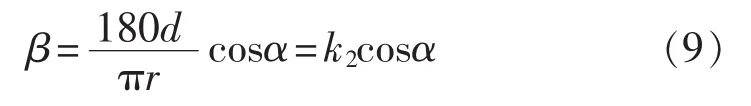
如表2所示,当α=0°且r=16mm时对β的理论值与实际测量值进行误差分析可得到,β与d的理论关系式与其拟合式(8)近似相同。同理,对多组α、r取值不同的待检区域进行实测分析可知,β是d的正比例函数,函数关系为式(7),即
2.2 验证被检区域旋转角度β与水平倾斜角α的关系
由式(5)可得:
当d,r的取值不变时,k2为常数,则β是α的余弦函数。为验证上述算法的效果,选取如图6所示d=6mm且r=16mm的产品为例进行实验。通过垂直投影法获取各被检区域的旋转角度β,其取值如表3所示。
采用最小二乘法对实验所得数据拟合,得到被检区域的旋转角度与被检区域水平倾斜角的拟合曲线如图7所示且拟合公式为

表2 当α=0°且r=16mm时β误差分析表

图6 不同倾斜角度的待检产品

表3 不同倾斜角α对应的旋转角度β的取值
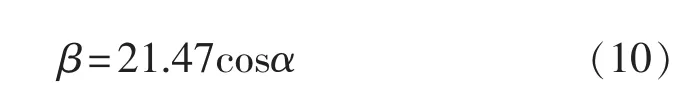
如表4所示,对β的理论值与实际测量值进行误差分析可知,β与α的理论关系式与其拟合式(10)近似相同。同理,对多组d、r取值不同的待检区域,进行实测分析可知,β是α的余弦函数,其函数关系式为式(9),即
2.3 验证被检区域旋转角度β与回转体半径r的关系
由式(5)可得:
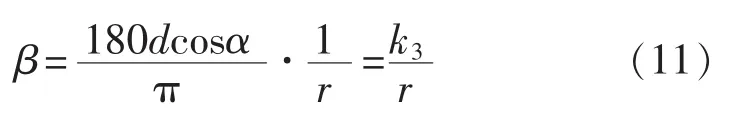

表4 当d=6mm且r=16mm时β误差分析表
当d,α取值不变时,k3为常数,则β是r的反比例函数。为验证上述算法的效果,选取如图8所示当α=0°且d=6mm时回转体半径不同的产品为例进行实验。通过垂直投影法获取各被检区域的旋转角度β,其取值如表5所示。
采用最小二乘法对实验所得数据进行拟合,得到被检区域的旋转角度与其所在回转体半径的拟合曲线如图9所示,拟合公式为

如表6所示,对β的理论值与实际测量值进行误差分析知,β与r的理论关系式与其拟合式(12)近似相同。同理,对多组α、d取值不同的待检区域进行实测分析可知,β是r的反比例函数,其关系为式(11)

图8 不同回转体半径的待检产品
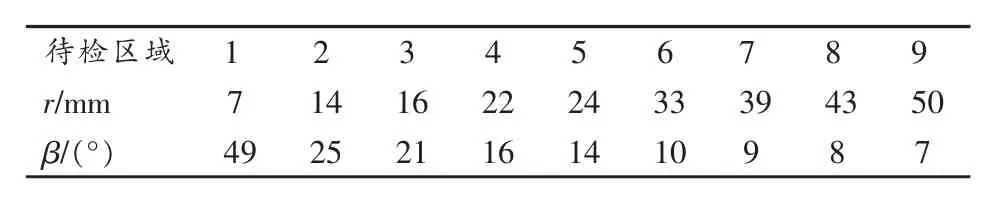
表5 各回转体半径r对应的旋转角度β的取值
2.4 实验结论
将理论上得到的函数关系表达式通过实验进行求解验证,得出产品各待检区域的采样步长均在95%的置信区间内,采样步长满足的函数关系为在实际工程应用中,由于待检区域的最大采样步长均取整数,且检测区域客体的最小待识别结构尺寸d、空间畸变α、弧度畸变r由设计与加工图纸已确定为已知信息,故将已知信息带入计算并取最大整数解即为该区域的最优采样步长。

图9 被检区域旋转角度与回转体半径的拟合曲线

表6 当α=0°且d=6mm时β误差分析表
3 结束语
本文从理论上推导出采样步长的函数关系表达式并通过实验对函数关系进行求解验证,为各待检区域采样步长的确定提供了理论依据。相对于固定旋转步长的采样机制,采用变步长采样机制根据不同信号实现频率自适应调节,提高了获取信息的利用率,即减少了数据冗余。
[1]崔明,顾启民,黄震.基于机器视觉的轴承滚动体缺陷检测算法研究[J].组合机床与自动化加工技术,2015,11(3):75-78.
[2]赵大兴,原振方,王博.基于机器视觉FPC缺陷检测对位系统研究[J].制造业自动化,2015,23(3):107-112.
[3]赵静.产品快速自动识别的变步长采样机制研究[D].太原:中北大学,2015.
[4]王一丁,段强宇,崔家礼,等.多参数融合的手背静脉图像质量评价[J].小型微型计算机系统,2016,37(4):870-876.
[5]SUPRIYA S, PATIL W.On-line defect detection of aluminum coating using fiber optic sensor[J].Photonic Sensors,2015,51(5):34-36.
[6]王冲.基于VB的可视化电子听诊器系统设计[J].电子世界,2014,24(12):515-517.
[7]徐青.基于变步长采样的产品装配结构正确性自动检测技术研究[D].太原:中北大学,2014.
[8]徐青,韩跃平,杨志刚,等.基于最优识别区间的变步长产品表面缺陷检测研究[J].激光与光电子学进展,2013,10(10):90-96.
[9]RAN L F.An algorithm of characters segmentation based on based on vertical projection for license plate[J]. Communications Technology,2012,45(4):89-91.
[10]崔文学,崔义川,王朝晖,等.基于模板匹配和垂直投影的车牌字符分割算法[J].齐齐哈尔大学学报(自然科学版),2015,11(6):12-16.
[11]DINH H, JOVANOV E,AAHAMIR.Eyes blink detection using intensity vertical projection[J].Engineering and Technological Innovation,2012,11(5):40-43.
[12]WANG L Y. Properties of the total least square estimation[J].Geodesy and Geodynamics,2012,23(4):39-46.
[13]张永昌.基于最小二乘拟合的数值分析方法在织物染色配色中的应用研究[D].青岛:青岛大学,2011.
[14]SUN L P,WEIY M,ZHOU J Y.On an iterative method for solving the least squares problem of rankdeficient systems[J]. International Journal of Computer Mathematics,2015,3(4):532-541.
(编辑:刘杨)
Research on variable-step sampling mechanism in inspection of product surface
GUO Jing,HAN Yueping,JIA Zhiqian,LI Huige
(School of Information and Communication Engineering,North University of China,Taiyuan 030051,China)
For product surface defect detection,a method of data acquisition based on variable-step self-adaption was proposed to achieve frequency modulation on sampling basis of signal changes due to large data redundancy and low efficiency caused by fixed-step data collection.Firstly,the function relationship expression for sampling step was deduced according to the influence factors(Nyquist sampling theory,identifiable size,radian distortion and space distortion)of sampling step. Secondly,it is specifically analyzed and verified that the sampling step(obtained by using the formula)of each area of verified product is within 95%of confidence interval based on the Matlab simulation platform and the method of least squares fitting.The test results show that the deduced sampling step formula provides a theoretical basis for reasonable selection of rotation step in each area to be inspected.The mode can implement adaptive adjustment of frequency according to different signals,which can improve efficiency of data acquisition and reduce data redundancy.
data acquisition;variable-step sampling;data fitting;surface defect
A
:1674-5124(2017)02-0020-05
10.11857/j.issn.1674-5124.2017.02.004
2016-05-29;
:2016-07-21
国家自然科学基金(61171178);山西省自然科学基金(2012011010-3)
郭 静(1990-),女,山西太原市人,硕士研究生,专业方向为X射线无损检测与图像处理技术。
韩跃平(1974-),男,山西太原市人,教授,博士,研究方向为X射线无损检测、图像处理与模式识别等。

