基于MEMS传感器的高精度姿态角测量研究
刘 震,王雪梅,倪文波
(西南交通大学机械工程学院,四川 成都 610031)
基于MEMS传感器的高精度姿态角测量研究
刘 震,王雪梅,倪文波
(西南交通大学机械工程学院,四川 成都 610031)
针对传统姿态参考系统姿态解算容易受到载体运动加速度的干扰,导致系统精度变低、稳定性变差等问题,提出一种改进的卡尔曼滤波算法。该算法建立基于四元数的惯性系统姿态解算数学模型,并根据载体运动加速度的大小,适时调整卡尔曼滤波器的量测噪声方差的大小,以此减弱卡尔曼滤波过程中运动加速度对姿态角解算精度的影响。采用MEMS三轴陀螺仪、加速度计和磁阻传感器完成载体在电梯升降过程中的测量,对实验测量数据进行姿态解算,结果表明改进后的卡尔曼滤波算法能够有效减小运动加速度对姿态解算的影响,姿态角的均方根误差相对于传统的姿态参考系统降低约40%。
姿态解算;运动加速度;互补滤波;卡尔曼滤波;MEMS传感器
0 引 言
载体的姿态角是描述载体坐标系与地理坐标系相对位置的物理量,可以确定载体在空间中所处状态。姿态角测量系统广泛应用于军事、航空航天、航海、无人机、机器人、人体姿态识别[1-3]等方面。高精度的姿态角测量系统一般采用高精度的机械陀螺仪或激光陀螺仪,但是价格昂贵。随着微机电系统(microelectro-mechanical systems,MEMS)惯性传感器[4]以及计算机技术的迅速发展,姿态角测量系统逐渐向低成本、小型化和高精度发展。MEMS陀螺仪、加速度传感器和磁阻传感器被广泛用于姿态角的测量中。惯性系统通过陀螺仪测量载体旋转过程中的角速度,并对角速度积分得到载体的姿态角。然而MEMS陀螺仪较大的漂移误差[5],致使积分得到的姿态角存在较大的累积误差,长时间使用的精度较差。由加速度传感器和磁阻传感器组成的姿态参考系统[6],以当地的重力加速度和地磁向量作为参考,由此计算出载体倾角和航向角。姿态参考系统具有良好的静态特性,不存在累积误差,但在动态情况下容易受到载体运动加速度和环境磁场等因素的干扰[7-8]。
解决上述问题通常采用互补滤波[9]和卡尔曼滤波[10]两种方法。陀螺仪的动态特性好,而姿态参考系统的静态特性好,互补滤波法就是根据各传感器在频域上的互补特性,对两个系统的传感器信息进行融合,来得到更准确的姿态角估计。互补滤波方法的效果很大程度上取决于截止频率的选择,但由于载体运动的随机性,实际应用中很难确定一个最佳的截止频率。卡尔曼滤波则利用GPS、加速度传感器或磁阻传感器等外部观测信息对惯性系统的姿态角误差进行补偿[11],来得到更加可靠的姿态角估计值,却难以消除运动加速度对姿态角估计的影响。
基于此,本文在分析比较传统滤波估计方法的基础上,利用直接安装在载体上的MEMS陀螺仪、加速度传感器和磁阻传感器构成测量系统,采用一种改进的卡尔曼滤波方法对载体的姿态角进行估计,通过识别运动加速度以调整卡尔曼滤波器中测量噪声方差的大小,来减小运动加速度对姿态估计的影响,从而提高姿态角的估计精度。
1 姿态角求解原理
导航系统中载体的姿态角通常使用俯仰角θ、横滚角γ、航向角φ来描述。载体姿态的变化是指载体坐标系相对于参考坐标系的空间转动,由欧拉定理[12]可知,载体坐标系相对于参考坐标系的转动可通过3次独立的旋转来实现。以地理坐标系XnYnZn为参考坐标系,坐标轴Xn、Yn、Zn分别指向东、北、天方向,假设初始载体坐标系XbYbZb与参考坐标系重合。载体的姿态角依次按如下的基本旋转确定:旋转过程如图 1[12]所示。

图1 载体姿态角的确定
地理坐标系XnYnZn与载体坐标系XbYbZb的空间关系可由下式表示:


计算坐标之间的相对转动关系主要有两种方法:欧拉角法和四元数法[13]。相对于欧拉角法,四元数法不仅可全角度描述姿态,避免了欧拉角的奇异问题,而且计算快捷,所以本研究采用四元数法计算载体姿态角。四元数与姿态矩阵的关系为
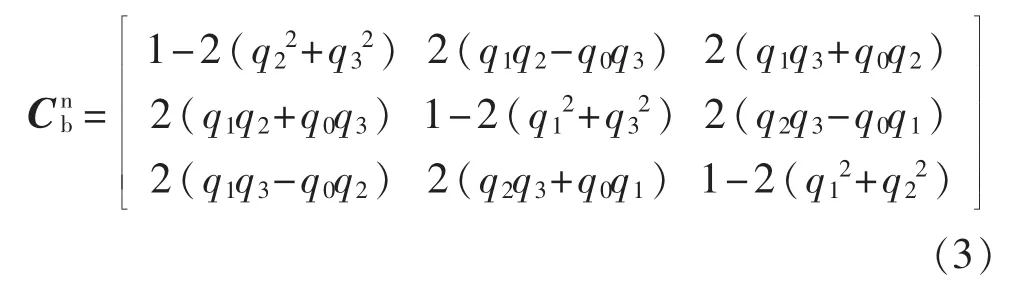
由捷联惯性四元数相关理论[12],得四元数的微分方程为

采用比卡算法或龙格库塔算法[14]求解微分方程(4),得到四元数的4个值,进而计算出姿态矩阵(3)。 其中 ωx、ωy、ωz由下式计算得到:

ωie——地球自转角速率;
R——地球平均半径;
L——载体所在的纬度;
VE、VN——载体的东向速度和北向速度。
1.1 惯性系统解算方法
惯性系统解算姿态角是通过陀螺仪测量载体的角速度,对角速度积分得到载体的姿态角。由四元数理论,其姿态角计算公式为

1.2 姿态参考系统解算方法
姿态参考系统由加速度传感器和磁阻传感器组成。由加速度传感器测量值可确定载体的俯仰角θ和横滚角γ,结合磁阻传感器测量值可进一步解算出航向角φ。当载体坐标系相对于地理坐标系静止时,加速度传感器测量输出满足下式:

式中:ax、ay、az——载体静止时加速度传感器在3个坐标轴方向的测量值;
g——载体所在地的重力加速度。
由式(7)可得俯仰角θ和横滚角γ的计算式:

地球磁场在地理坐标系中的分量与磁阻传感器的测量值满足下式:
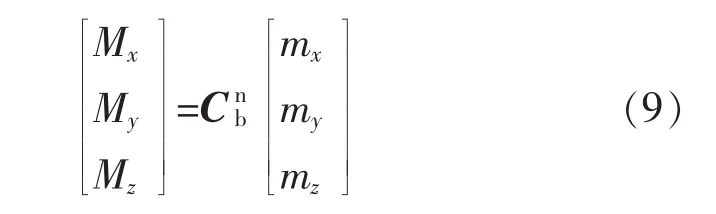
式中:mx、my、mz——磁阻传感器在3个坐标轴方向的测量值;
Mx、My、Mz——载体在地理坐标系下的三轴磁场值。
由于航向角的大小与加速度传感器的输出无关[15],故可假设航向角φ=0°。把由加速度传感器解算出的俯仰角θ和横滚角γ代入Cbn中,由式(9)可得:

航向角可由下式计算得到:

2 传感器信号预处理
载体运动时,直接安装在载体上的MEMS传感器易受各种高频振动干扰,对姿态解算不利,必要的低通滤波处理可以提高信号的信噪比,使姿态角的解算结果更加准确、可靠。
磁阻传感器使用时会受周围磁性物质干扰,使得磁阻传感器的输出不能准确反映地球磁场矢量,其间的误差称为“罗差”。常使用最小二乘误差补偿法和椭圆假设补偿法对“罗差”进行补偿,由于最小二乘误差补偿法需借助高精度的转台才能完成,而椭圆假设补偿法不需要借助任何工具,并且效果理想,故本文采用椭圆假设补偿法对“罗差”进行补偿。
椭圆假设补偿法是基于“罗差”对输出结果的宏观影响来设计的[15],在理想情况下,将磁阻传感器在水平面旋转一周,其X轴输出和Y轴输出画在同一个坐标系里,理论上会得到一个圆心在原点的圆,由于受周围磁性物质的干扰,其结果往往是圆心不在原点的椭圆,如图2中蓝色椭圆所示;通过椭圆假设补偿法校正后,结果如图2中红色圆所示。如校正前mx=-0.0162Gs,my=-0.0176Gs;对应校正后mx=-0.0110Gs,my=-0.0118Gs。

图2 磁阻传感器“罗差”校正前后比较
3 基于四元数的改进卡尔曼滤波算法
惯性系统姿态角解算方法具有良好的动态特性,但存在较大的随时间累积的误差;姿态参考系统静态特性好,且不存在累积误差。利用卡尔曼滤波方法,可以把两个系统有效地结合起来,优势互补,提高姿态角估计计算精度。为此需建立相应的状态空间方程和观测方程。以惯性系统解算的姿态角误差Δθ、Δγ、Δφ作为状态变量, 惯性系统解算的姿态角θINS、γINS、φINS与姿态参考系统解算的姿态角 θAZ,γAZ,φAZ之差作为观测变量Z。考虑传统的卡尔曼滤波方法难以消除运动加速度对姿态角估计的影响,本文根据载体运动加速度的大小,适时调整卡尔曼滤波器的量测噪声方差R的大小,以此来减弱运动加速度对姿态角估计精度的影响。如果运动加速度的绝对值|as|大于阈值Δ,则量测噪声方差选取R2,否则量测噪声方差选取R1,且R2>R1。惯性系统的初始四元数Q(0)通过姿态参考系统确定,以保证惯性系统初始姿态的准确。最后,用惯性系统解算的姿态角θINS、 γINS、φINS减去卡尔曼滤波器估计的姿态角误差φ,得到补偿后的姿态角解算姿态角之前,对传感器数据进行预处理。本文的姿态角解算原理框图如图3所示。
选取载体的3个姿态角误差作为状态变量,卡尔曼滤波器的数学模型如下:
状态空间方程:

观测方程:

其中状态向量X=[ΔθΔγΔφ];F为状态转移矩阵,由式(14)确定,式中h为载体所在地的高度;G为噪声驱动矩阵;W为过程噪声向量,假设为零均值高斯白噪声;Z为观测量,由式(15)确定;H为观测矩阵,H=I3×3;V为观测噪声向量,也假设为与W和观测信号不相关的、零均值高斯白噪声。

卡尔曼滤波过程如下:
根据卡尔曼滤波的基本方程,得到状态一步预测:

Fk,k-1——k-1时刻到k时刻的一步转移矩阵;
Gk,k-1——k-1时刻到k时刻的系统噪声驱动矩阵;
Wk——k时刻的过程噪声。
一步预测误差方差阵:
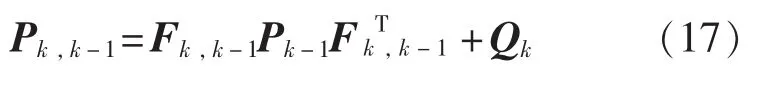

图3 姿态解算算法原理框图
式中:Pk,k-1——利用k-1时刻的误差方差阵预测k时刻的误差方差阵;
Pk-1——k-1时刻的误差方差阵;
Qk——k时刻的过程噪声方差阵。
状态估计:

Kk——k时刻的增益矩阵;
Zk——k时刻的观测值;
Hk——k时刻的观测矩阵。
滤波增益矩阵:

式中Rk是k时刻的量测噪声方差阵。
估计误差方阵:
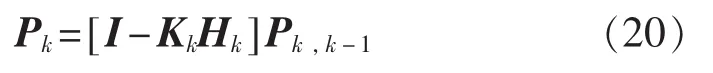
式中I为单位阵。
Rk的取值由下式确定:

式中R2>R1,具体的大小可根据经验选取;|as|为运动加速度的模,Δ为判断是否存在运动加速度的阈值,实际应用中,其大小按照经验值设置。当存在较大的运动加速度时,Rk增大,Kk减小,减弱了姿态参考系统对应的观测量在状态估计中的权重,相对的增大了惯性系统预测值的权重,以此来削弱运动加速度对姿态角估算精度的影响。
4 实验验证及结果分析
本文的姿态角测量系统以STM32芯片为核心,由MPU6050传感器(包括三轴陀螺仪和三轴加速度传感器)和HMC5883L三轴磁阻传感器组成。STM32芯片通过I2C接口读取3个传感器测量的数据,再由串口把数据发送到PC计算机进行保存和进一步数据处理。
为了分析载体运动加速度对姿态解算精度的影响,本文特别设计了一个运动模型,利用电梯升降过程中存在的运动加速度检测其对姿态解算精度的影响。将测量单元安装在45°角的三角木块的倾斜表面,如图4所示,测量电梯在升降过程中角速度、加速度和磁场的变化。
让安装有测量单元的三角木块固定于电梯地面,电梯从1楼静止开始上升,2楼经停,最终停在3楼,实验时长57 s,电梯在每层楼启停的过程中都存在运动加速度。3个轴的加速度测量值如图5所示,从图中可以看出Y轴和Z轴存在明显运动加速度。加速度数据中存在高频干扰,可对其进行低通滤波处理。

图4 测量单元安装示意图
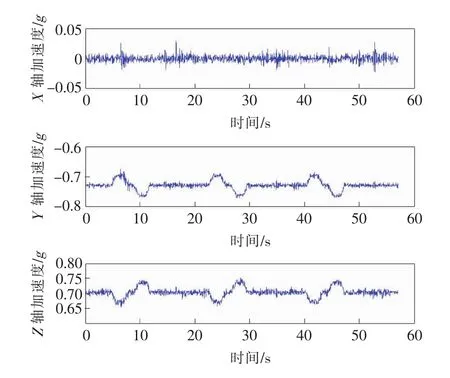
图5 三轴加速度测量值
分别采用惯性系统解算法和姿态参考系统解算法对载体姿态角进行解算,结果如图6所示。从图中可以看到,惯性系统通过积分解算得到的3个姿态角存在明显的随时间的累积误差;姿态参考系统解算得到的俯仰角在含有运动加速度的时间段里,存在明显的角度误差。航向角由于周围磁性物质的干扰,也有较大的误差。

图6 惯性系统和姿态参考系统的姿态角比较
使用互补滤波算法进行姿态解算,其姿态角误差如图7所示。从图中可以看到,互补滤波解算结果不存在像惯性系统一样的累积误差,受运动加速度的影响也较小,但是可以看到,其初始阶段存在较大的误差;而且截止频率fc的大小对滤波效果有明显影响:fc越大,误差的收敛速度越快,但并不是fc越大精度越高。从航向角误差图中可以看出,互补滤波算法的fc很难有一个最优的选择。虽然使用PI调节和互补滤波相结合的算法[16],可以提高误差的收敛速度,但是会导致超调和振荡等问题。

图7 互补滤波算法计算的姿态角误差
使用卡尔曼滤波算法进行姿态估算,从图5中可以看到,Y轴和Z轴存在运动加速度,识别Y轴方向的运动加速度取as=ay-ay0,ay0是Y轴加速度的第1个测量值。识别Z轴方向的运动加速度取as=az-az0,az0是Z轴加速度的第1个测量值。在卡尔曼滤波过程中,据此通过式(21)调整测量噪声方差大小,根据本实验的测试数据,取R1=0.012,R2=0.0252,Δ=0.01g。卡尔曼滤波解算的姿态角误差如图8所示。从图中可以看出,改进后的卡尔曼滤波在含有运动加速度的时间内,输出的姿态角精度比一般的卡尔曼滤波高;对比互补滤波算法,虽然互补滤波消除了运动加速度的干扰,但其初始误差大,且过程中有较大的振荡。
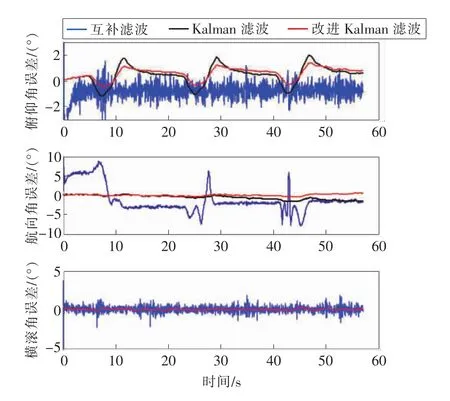
图8 卡尔曼滤波与互补滤波比较
以下式计算各种姿态角算法的均方根误差,结果如表1所示。
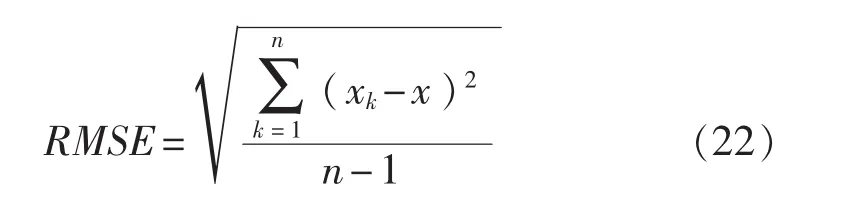
式中:n——数据长度;
xk——k时刻解算出的姿态角值;
x——姿态角真实值。
从表中可以看出,姿态参考系统对磁场进行校正后,航向角的精度提高了。互补滤波算法随着截止频率fc增大,俯仰角和横滚角的精度得到提高,但是航向角的精度并没有得到明显改善。互补滤波算法结合PI调节后,精度有所提高,但其仍然比不上卡尔曼滤波算法的精度。改进的卡尔曼滤波算法,由于能根据载体运动加速度对量测噪声方差R进行调整,削弱了运动加速度对姿态角的影响,能获得更高的姿态角解算精度。从俯仰角的解算结果可以得到,改进卡尔曼滤波算法相对于姿态参考系统均方根误差降低了约40%。
在上述相同的实验条件下,当电梯升降时使俯仰角的大小改变,相应的测量、解算结果如图9所示。从图中可以看出,惯性系统俯仰角解算结果存在明显的随时间的累积误差。姿态参考系统解算出的俯仰角在含有运动加速度的时间段里,也存在明显的角度误差,其分别出现在8~12s,19~23s,45~49s的时间段内,最大角度误差达到14°。这是由于俯仰角越大,Y轴的重力加速度分量就越接近重力加速度g,俯仰角对载体的运动加速度就越敏感,由此引起的俯仰角误差越大。对比一般的卡尔曼滤波算法与本文提出的改进卡尔曼滤波算法,在含有运动加速度的时间段里,改进卡尔曼滤波算法可以减小运动加速度对俯仰角解算的影响,与俯仰角不变情况下实验结论相同。

表1 各种姿态角算法的均方根误差比较
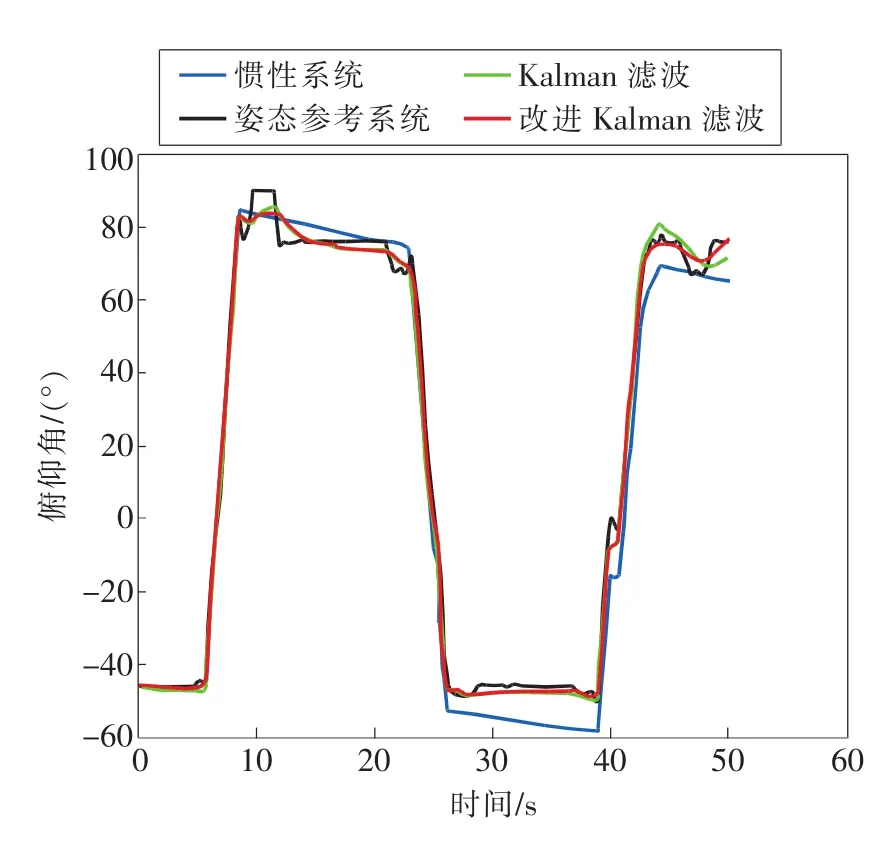
图9 惯性系统、姿态参考系统和卡尔曼滤波的俯仰角比较
5 结束语
本文针对运动加速度对姿态参考系统姿态角解算的影响,提出了一种改进卡尔曼滤波算法。该算法能根据载体运动加速度的大小,适时调整卡尔曼滤波器的量测噪声方差,来减小姿态参考系统对应的观测变量在卡尔曼滤波过程中的权重,相对的增大惯性系统在卡尔曼滤波过程中的权重,以此削弱运动加速度对姿态角解算的影响。通过对含有运动加速度的实验数据进行姿态解算,对比经典的互补滤波算法和传统的卡尔曼滤波算法,表明本文提出的改进后的卡尔曼滤波算法能够有效减小运动加速度对姿态解算的影响,获得更高精度的姿态角解算结果。
[1]吕印新,肖前贵,胡寿松.基于四元数互补滤波的无人机姿态解算[J].燕山大学学报,2014(2):175-180.
[2]万良金.基于多传感器信息融合的机器人姿态测量技术研究[D].北京:北京交通大学,2015.
[3]杜波,刘奭昕.人体姿态检测装置的设计[J].长春工程学院学报(自然科学版),2012,13(4):105-107.
[4]陈曦.基于MEMS惯性传感器的高精度姿态测量关键技术研究[D].杭州:浙江大学,2014.
[5]陈旭光,杨平,陈意.MEMS陀螺仪零位误差分析与处理[J].传感技术学报,2012,25(5):628-632.
[6]米刚,田增山,金悦,等.基于MIMU和磁力计的姿态更新算法研究[J].传感技术学报,2015(1):43-48.
[7]张秋阳.无人机姿态测算及其误差补偿研究[D].长沙:中南大学,2011.
[8]卢志才,高敏,贾春宁.基于地磁测量的火箭弹滚转角解算误差补偿方法研究[J].中国测试,2014,40(2):9-12.
[9]VASCONCELOS J F,CARDEIRA B,SILVESTRE C,et al.Discrete-time complementary filters for attitude and position estimation: design, analysis and experimental validation[J].IEEE Transactions on Control Systems Technology,2011,19(1):181-198.
[10]BRIGANTE C M N,ABBATE N,BASILE A,et al. Towardsminiaturization ofa MEMS-based wearable motion capture system[J].IEEE Transactions on Industrial Electronics,2011,58(8):3234-3241.
[11]GAO C,ZHAO G,LU J.In-flight misalignment attitude estimation for UAV based on GPS and UKF/MPF filter[C]∥Guidance,Navigation and Control Conference(CGNCC), 2014 IEEE Chinese.IEEE,2015:452-457.
[12]秦永元.惯性导航[M].2版.北京:科学出版社,2014:130-136.
[13]陈亮.基于对偶四元数的捷联惯性导航算法[D].哈尔滨:哈尔滨工业大学,2011.
[14]王励扬,翟昆朋,何文涛,等.四阶龙格库塔算法在捷联惯性导航中的应用[J].计算机仿真,2014,31(11):56-59.
[15]徐昺.基于MEMS传感器与ZigBee网络的人体动作捕捉系统的设计与实现[D].成都:电子科技大学,2013.
[16]郭晓鸿,杨忠,陈喆,等.EKF和互补滤波器在飞行姿态确定中的应用[J].传感器与微系统,2011,30(11):149-152.
(编辑:莫婕)
Research on attitude angle measurement with high precision based on MEMS sensors
LIU Zhen,WANG Xuemei,NI Wenbo
(School of Mechanical Engineering,Southwest Jiaotong University,Chengdu 610031,China)
Since the conventional attitude and heading reference system are vulnerable to the interference of motion acceleration,an improved Kalman filter algorithm was proposed in the paper. Quaternion attitude mathematical model based on inertial system was built up.The improved Kalman filter algorithm can reduce the impact of motion acceleration on attitude algorithm in the process of Kalman filter by timely adjusting the observation noise variance according to the motion acceleration of vehicle.The experimental data were measured by MEMS three-axis gyroscope,accelerometer and magnetoresistive sensors during riding up and down in the elevator.The results demonstrate that the improved Kalman filter algorithm can significantly reduce the impact of motion acceleration on attitude estimation.And compared to traditional attitude and heading reference system,attitude RMSE with improved Kalman filter algorithm has decreased by 40%.
attitude estimation;motion acceleration;complementary filtering;Kalman filter;MEMS sensor
A
:1674-5124(2017)02-0006-07
10.11857/j.issn.1674-5124.2017.02.002
2016-06-12;
:2016-07-22
刘 震(1990-),男,陕西西安市人,硕士研究生,专业方向为测控技术及应用。
王雪梅(1968-),女,副教授,博士,研究方向为现代测控技术及其在轨道交通中的应用。

