单轴压缩下砂岩声发射及分形特征研究
张 昕,付小敏,沈 忠,黄兴建
(成都理工大学 地质灾害防治与地质环境保护国家重点实验室,四川 成都 610059)
单轴压缩下砂岩声发射及分形特征研究
张 昕,付小敏,沈 忠,黄兴建
(成都理工大学 地质灾害防治与地质环境保护国家重点实验室,四川 成都 610059)
为研究砂岩在单轴压缩下声发射及分形特征,在MTS815程控伺服刚性试验机上,对早古生代志留系下统小河坝组(S1x)砂岩进行单轴压缩下的声发射试验,结合声发射特征参数、应力应变关系以及分形特性,对岩石整个失稳破坏过程进行分析。结果表明:小河坝组砂岩声发射及分形特征、力学特性在岩石损伤破裂过程中具有一致性,以应力比0.6~0.8之间振铃计数率的变化趋势段作为岩体失稳与破坏的识别方法;相空间维数的选取对关联维数有一定影响,随相空间维数m的增加,关联维数D呈现出增加-稳定-发散的发展过程;声发射序列在应力比为0.3~0.5时,关联维数D值最大;声发射序列关联维数曲线表现为“波动-上升-下降-波动”的演化模式,在较高应力比0.7~0.8时,关联维数D在介于0.9~1.4之间小幅波动。据此,可为工程中岩体失稳与破坏的监测预报提供一定的理论基础与数据支撑。
单轴压缩;砂岩声发射;振铃计数率;分形;关联维数
0 引 言
砂岩在失稳破坏过程中的声发射参数及分形特征,能够为试样内部的损伤变化的发展过程和获取合理的岩石破坏前兆提供判断依据,对边坡失稳破坏的预测以及防治具有重要的理论及实践意义[1]。同时,不少文献表明将分形理论与岩石声发射相结合,可以更好地描述裂纹发展规律[2]。Ganne等[3]研究了脆性岩石的声发射特性,分析其岩石声发射与微破裂之间的关系。Kusunose等[4]以不同纹理分布的花岗岩为研究对象,在三轴压缩试验条件下,对声发射事件空间分布的分形维数的规律进行分析。高保彬等[5]研究了单轴压缩下不同破坏类型岩石的声发射及分形特征,指出岩石声发射序列分维值在塑形破坏时的突降持续时间要比脆性破坏长。吴贤振等[6]对不同岩石的失稳破坏过程中声发射及其分形特征进行了研究,认为声发射序列分形维数会出现由波动到持续下降的模式,并提出了出现持续下降模式可以作为岩体失稳破坏的前兆。梁忠雨等[7]在单轴压缩条件下对大理石和红砂岩声发射参数的分形特征进行了研究,发现在不同应力水平下,声发射过程参数具有不同的分形程度。高峰等[8]计算了岩石在不同应力水平下声发射时间序列的关联维数,得出分维数的降低意味着主断裂或破坏的形成。李元辉等[9]通过单轴受压岩石破坏声发射试验,对空间分布分形维值和震级-频度关系式中的b值进行了分析,认为声发射分形维数值和b值变化趋势相近。
综上所述,国内外学者对岩石声发射及分形特征进行了大量的研究,但是对综合分析岩石声发射及其分形特征、力学特性的一致性还鲜有报道,且本文考虑了地质时期对岩石本身的影响,对小河坝组砂岩进行单轴压缩下的声发射试验,分析力学特征和声发射特征并结合分形理论研究,旨在为工程岩体的失稳破坏提供预测前兆以及为监测预报工作提供参考依据。
1 岩石声发射试验
1.1 岩石试样的制备
为了考察小河坝组砂岩声发射及分形特征,本试验的岩石样品取自重庆某公路边坡距今约4.2亿年早古生代志留系下统介壳相小河坝组(S1x)深灰色粉砂岩,高程约580m。岩样均严格按照国际岩石力学试验规范的要求,加工成25 mm×25 mm×75 mm的长方体试样,并对两个加载端面仔细研磨,使其上下表面的平行度、平整度及其垂直度均满足试验要求。岩样基本信息,如表1所示。

表1 小河坝组砂岩试样的基本信息
1.2 试验设备及试验方法

图1 试验系统
试验采用加载控制系统和声发射监测系统两套装置配合完成,系统基本原理如图1所示。试验加载设备为美国MTS815程控伺服刚性试验机,框架整体刚度5 000 kN/mm,最大轴压3 000 kN,应变率适用范围10-7~10-2s-1。声发射监测设备采用声华公司生产的SAEU2S声发射系统(可同时采集幅度、振铃计数、能量等参数),对整个试验过程进行全程跟踪监测,设置采样频率2 500 kHz,采样长度(点数)2044,参数间隔500μs,外参(荷载)采集间隔1s,前置放大器增益值为40dB。本次试验对3组不同地质时期砂岩进行单轴受力变形直至破坏的全过程试验,加载方式首先采用荷载控制,速率10kN/min,荷载达10kN之后转换为位移控制,速率为0.1mm/min,直至试验结束。试验时,保持加载过程与声发射监测过程在时间上同步。为加强声发射探头与试样的耦合效果,在试样的长边中心涂抹适量凡士林,并用橡胶圈将探头牢牢固定在试件侧面。为了消除加载过程中试件上下端部摩擦和试验机传来外部噪音对声发射信号采集的影响,在试样端部粘贴医用胶布消除干扰。
1.3 参数选取
本次研究从试验得到的力学参数和声发射参数中选取密度、抗压强度等力学参数以及声发射振铃计数、振铃计数率、能量和能率等声发射参数,用来分析小河坝组砂岩破裂过程的声发射特征及声发射序列分形特征。声发射振铃计数是岩石内部结构变化的外在声学表现,反映声发射活动的强弱程度和岩石内部损伤的演化过程[10]。
2 砂岩声发射试验结果分析
对小河坝组砂岩进行单轴压缩全过程试验,同时保持加载过程与声发射仪监测过程在时间上同步。试样受力变形直至破坏,均经历了初始压密、弹性、塑性和峰后破坏4个阶段,且不同阶段对应着不同的声发射特征。下面在试验过程中采集到的试样应力-应变全过程参数和声发射特征参数的基础上对砂岩的力学特征和声发射特征进行分析。
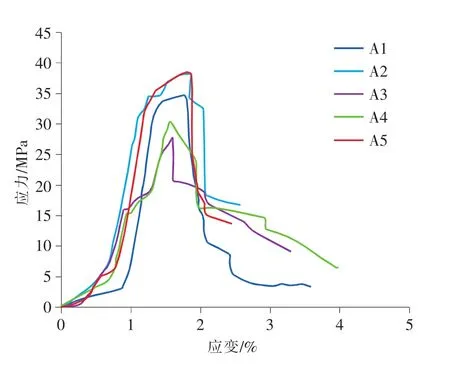
图2 单轴压缩下砂岩岩样应力-应变曲线图
2.1 单轴压缩下砂岩力学特征分析
根据试验结果绘制了砂岩A1~A5试样的应力-应变全过程曲线图,反映砂岩在单轴压缩下的变形强度特征,如图2所示。由此,试样的应力-应变全过程曲线可分为4个阶段,即初始压密阶段、弹性阶段、塑性阶段和峰后残余变形阶段。
从图中可以看出,在初始压密阶段,随着轴向应力的增加,砂岩试样中含有的原生微裂隙和孔隙或节理面被压密实发生闭合,轴向应变逐渐增大;在弹性阶段,岩石几乎无新裂纹产生,应力应变曲线近似于直线;随着应力的增加,塑性阶段产生不可逆的塑形变形,同时岩石内部大量微裂隙产生、扩展,在峰值应力前出现明显屈服阶段,最终导致试样宏观破坏。经统计,A1~A5试样的屈服点分别位于应力比(当前应力与峰值应力的比值)0.90,0.65,0.58,0.50,0.84。试样A3、A4因内部原生裂隙等的影响,在应力比0.5左右的位置曲线出现波动;峰后残余变形阶段,砂岩试样产生宏观断裂面或滑移面破坏失稳,但均仍因摩擦作用具有一定的承载能力,因此曲线在峰值后快速下降到某个值之后缓缓地下降到最低点。
2.2 单轴压缩下砂岩声发射特征分析
图3为单轴压缩下砂岩试样声发射振铃计数、累计振铃计数对数以及应力与时间曲线图,表2为不同应力比下声发射累计振铃计数统计表。可以看出,岩样A1~A5在加载全过程中声发射序列曲线呈现出一定的阶段性:在应力比0~0.2之间的初始压密阶段,试样中存在的原生微裂隙被压密实发生闭合及微结构面错动,声发射事件比较活跃,累计振铃计数不断增长,但各个试样累计振铃计数增长率大小不一,这表明了岩石的不均匀性以及各向异性的特点导致在同种岩性不同试样的结论中有所差异。随着应力的逐渐增加,岩石的原生裂隙被压实,声发射振铃计数水平较低,声发射累计振铃计数的增长变缓。在弹性阶段直至试样屈服前,新的微裂隙开始不断产生,声发射水平随之波动,各个试样声发射累计振铃计数均有不同幅度的快速增长。试样在塑性破坏阶段即应力比0.7~1之间,内部裂隙相互汇合贯通直至试样失稳破坏,均伴随有声发射活动的连续小幅增多或在某一时刻大幅增加,各个试样声发射振铃计数最大值分别为52 962,44 551,41 813,8429,20319。由图3(c)中砂岩A3试样和图3(d)中砂岩A4试样力学、声发射参数曲线图,结合应力-应变曲线可以得出,砂岩内部存在原生微裂隙,加载前期即A3试样在应力比0.2、A4试样在应力比0.4时其声发射活动由较低水平有了明显提升,声发射累计振铃计数对数曲线呈上升趋势,此后均在应力比约0.5时即试样屈服点附近声发射振铃计数出现跳跃式突增,试样外部出现宏观裂纹,声发射累计计数大幅增长,A3、A4试样在应力比0.4~0.5之间累计振铃计数增长率分别为647.7%、429.1%,加载后期声发射振铃计数水平很低,声发射累计振铃计数增长平稳缓慢,在应力比0.7~1之间累计振铃计数增长率分别为38.5%、16.3%。
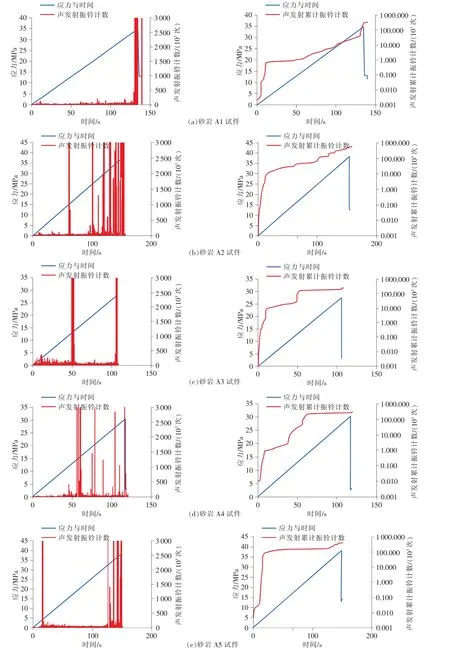
图3 砂岩岩样声发射计数、累计计数以及应力与时间关系曲线

表2 不同应力比下声发射累计振铃计数统计表
3 砂岩声发射序列分形特征分析
3.1 分形维数基本原理
分形几何学的主要概念是分形维数,分形维数是分形中最重要的特征参数,它可以定量描述分形。本文选用关联维数来计算分形维数值。Grassberger和Procaccia提出从时间序列直接计算关联维数D的算法,即G-P算法,是常用的关联维数计算方法[11]。本文将声发射振铃计数率序列作为研究对象,每一个声发射振铃计数率序列对应一个容量为n的序列集Xn={x1,x2,…,xn},再根据声发射振铃计数率序列集构成一个m维的相空间(m<n)。取前m个数作为m维空间的一个向量Xm={x1,x2,…,xm},然后右移一个数再取m个数构成向量为Xm+1={x2,x3,…,xm+1},以此类推,最后构成N=n-m+1个向量,即XN={xn-m+1,xn-m+2,…,xn}。因此,相应的关联维数为
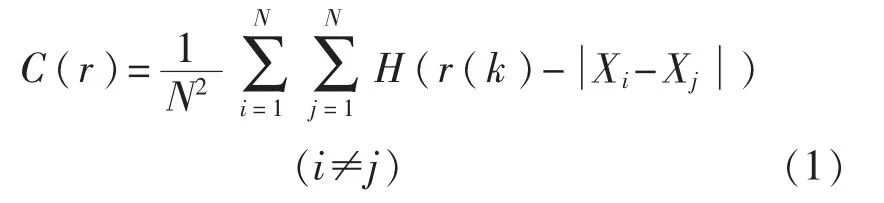
r(k)——给定的尺度函数。
为避免分散性,常取r(k)的计算公式为
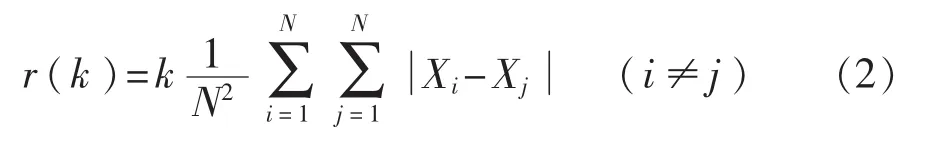
故对给定的每个尺度r(k),都对应一个 C(r)。对于给定的g个尺度,在双对数坐标系中可得到g个坐标点(lnC(r),lnr),再对这g个坐标点进行一元线性回归,若存在很好的相关性,回归直线的斜率就是声发射序列的关联维数D,即:

3.2 声发射参数的分形特征
相空间维数m对关联维数的取值有很大影响,因此,本试验中不同组别的声发射序列的关联维数计算应采用相同的相空间维数m值,以此保证结论的可比性。
以砂岩A2试样声发射振铃计数率序列为例,结合关联维数算法,运用Matlab软件,得到不同的相空间维数m和关联维数D的关系曲线,如图4所示。可以得出关联维数D随着相空间维数m的增加而增加,当相空间维数m在6~12时,关联维数D基本保持稳定,变化很小。这与文献[12]中提出的随着相空间维数m的增加,关联维数D呈现出增加-稳定-发散的发展过程相吻合。综上分析考虑,本文确定此时的m作为相空间的维数值,即相空间维数m=6。
对各岩石试样的声发射振铃计数率参数序列进行一元线性回归,回归直线的斜率就是声发射参数的关联维数D,所拟合的直线与原始数据具有很好的相关性,且相关系数均大于0.94(见表3),表明岩石损伤破裂过程中的声发射参数序列在时域上具有自相似性,也就是具有分形特征。
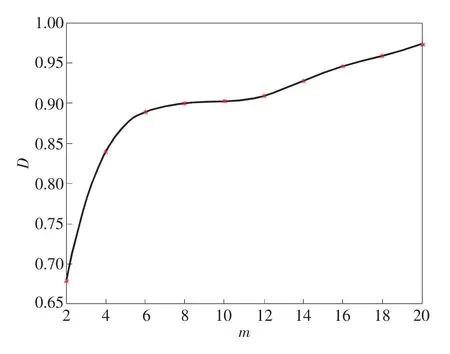
图4 相空间维数m与关联维数D关系曲线

表3 不同应力比下关联维数D与拟合相关系数r统计表
图5列出了砂岩的声发射振铃计数率关联维数D值随着应力的变化而变化的关系曲线,不同应力比时关联维数D统计,如表3所示。关联维数D作为岩石内部微裂纹无序性的度量,可以很好地表征内部损伤破坏的发展演化规律。从不同应力比时声发射序列关联维数的变化来看,结合单轴压缩下砂岩试样声发射振铃计数、累计振铃计数以及应力与时间曲线,可以得知在加载初期,每个岩石试样内部整体存在尺度较小的初始微裂隙和原生节理面或缺陷的空间分布各不相同、无序无规律。在逐渐增加的荷载作用下,初始微裂隙和原生节理面或缺陷被压密实发生闭合或扩展,关联维数D值波动起伏,而后在弹性阶段即应力比0.3~0.5时,关联维数D达到最大;随着荷载的增加,岩石试样内部裂纹汇合贯通,大尺度微裂纹增多,逐渐形成局部性损伤破坏,微裂纹的分布变得规律有序,此时关联维数D持续下降;当应力比较高时,应力集中作用在主破裂面,关联维数D值在较小的变化区间内波动。
从以上声发射序列分形特征讨论分析中可得,岩石破坏过程中声发射振铃计数率存在分形特征,据此求出的关联维数能够很好地表征岩石内部损伤破坏的发展过程。随着应力比的增大,关联维数D呈“波动-上升-下降-波动”的变化形式。谢和平[2]在研究中表明岩石破坏过程是一个有序降维的过程,徐志斌等[13]指出分维值D的变化可以很好地反映试样内部微裂纹的发展及演化,尹贤刚等[14]在试验研究中也证实了这些结论。本文通过单轴压缩下砂岩声发射试验研究表明,砂岩在破坏前阶段即应力比0.7~0.8,关联维数D值在一定范围内波动,可为工程中岩体失稳与破坏的监测预报提供一定的理论基础与数据支撑。
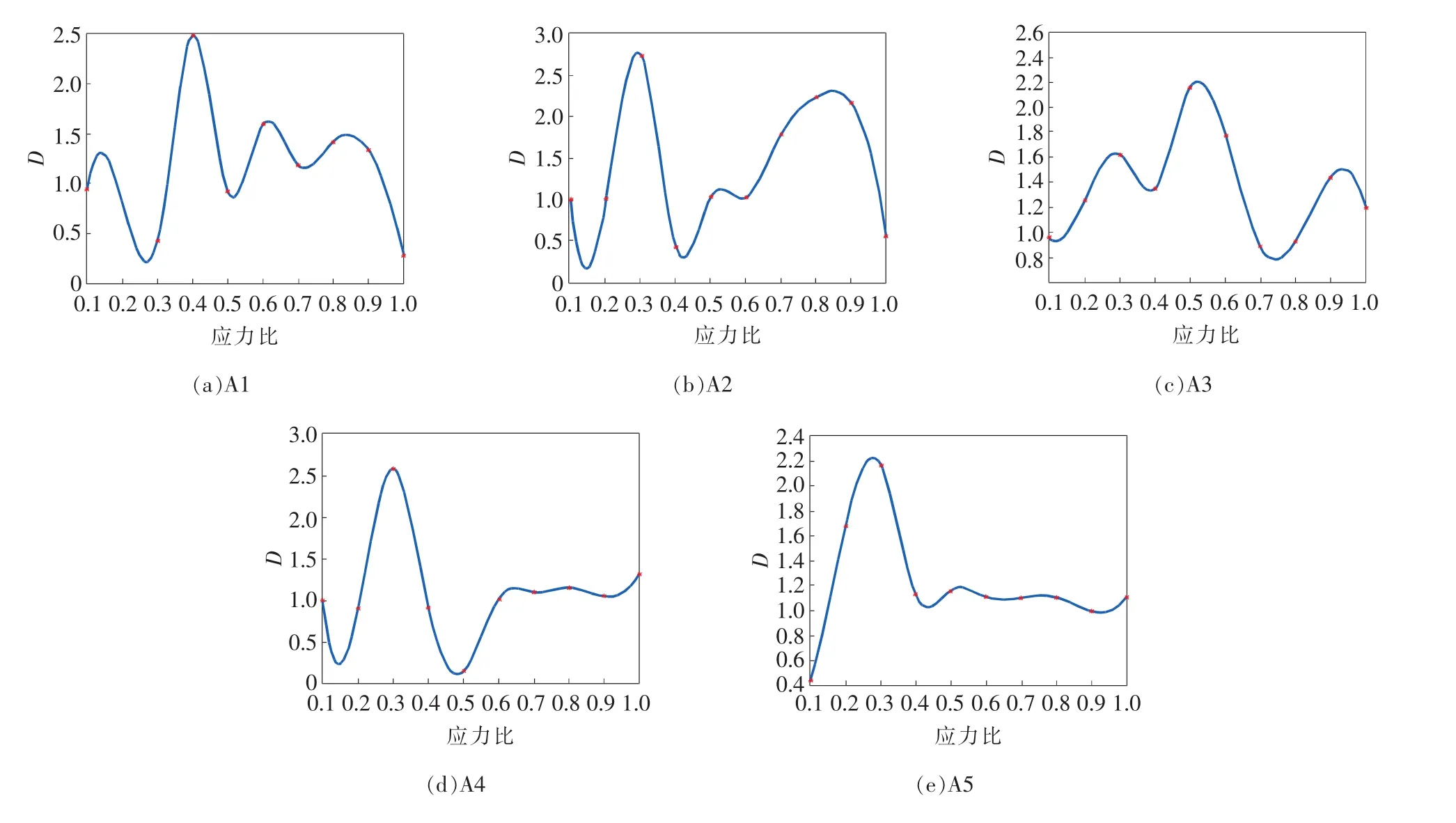
图5 不同应力比对应关联维数D的变化曲线
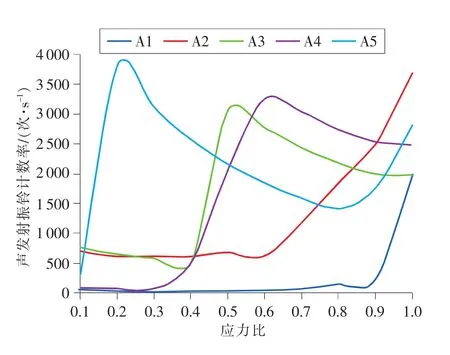
图6 不同应力比对应声发射振铃计数率变化曲线
4 砂岩声发射与分形特征分析
本文通过岩石声发射振铃计数率序列计算得出的关联维数D值随应力比的变化而变化的趋势与加载过程中岩石声发射累计振铃计数的统计规律具有很好的一致性。图6为不同应力比对应的声发射累计振铃计数率变化曲线。结合前文声发射分形特征的分析,可以得出,从加载开始即初始压密阶段至弹性阶段,试样中存在的原生微裂隙被压密实发生闭合及微结构面错动,在不同应力比下声发射累计振铃计数逐渐增长,随着时间的累积,声发射振铃计数率呈现稳中有降的趋势,其中A5试样由于在加载初期发生大量声发射现象,其声发射振铃计数率曲线出现急速上升现象。关联维数D值在此期间波动变化,在应力比0.3~0.5时,声发射振铃计数率变化幅度较小,意味着岩石整体内部微裂纹在空间中分布均匀,关联维数D值上升达到最大。随后试样均在接近屈服点处声发射累计振铃计数突增,声发射振铃计数率曲线大幅上升,表明岩石内部裂纹开始汇合、扩展、贯通,随着应力的不断增加,岩石局部形成一些主破裂带,关联维数D值从最大值下降后持续小幅波动直至试样破坏。
5 结束语
1)在试验过程中,声发射振铃计数曲线和振铃计数率曲线及其分形特征与应力-应变曲线具有很好的一致性,相互结合能够更好地呈现岩石失稳破坏的整个过程,并以屈服点后即应力比0.6~0.8之间振铃计数率的变化趋势段作为岩体失稳与破坏的识别方法,为工程中岩体失稳与破坏的监测预报提供一定的依据。
2)小河坝组砂岩声发射振铃计数率的关联维数D值呈现出“波动-上升-下降-波动”的演化模式,并且应力比在0.3~0.5内达到峰值,在岩样破坏前即应力比0.7~0.8内小幅波动,可以作为岩石破坏失稳的前兆。
3)小河坝组砂岩试样在加载破坏前,关联维数D值介于0.9~1.4,这可作为边坡失稳破坏预测和判断声发射源的参考依据。
[1]王东升,汤鸿霄,栾兆坤.分形理论及其研究方法[J].环境科学学报,2001,21(增刊):10-16.
[2]谢和平.分形-岩石力学导论[M].北京:科学出版社,1996:57-64.
[3]GANNE P,VERVOORT A,WEVERS M.Quantification of pre-peak brittle damage:Correlation between acoustic emission and observed micro-fracturing[J].International Journal of Rock Mechanics and Ming Science,2007,44(4):720-729.
[4]KUSUNOS K,LEIX L,NISHIZAWAOSAMU,et al. Effect of grain size on fractal structure of acoustic emission hypocenter distribution in granitic rock[J].Physics of the Earth and Planetary Interiors,1991,67(1-2):194-199.
[5]高保彬,李回贵,李化敏.不同破坏类型岩石的声发射及分形特征研究[J].地下空间与工程学报,2015,11(2):358-363.
[6]吴贤振,刘祥鑫,梁正召,等.不同岩石破裂全过程的声发射序列分形特征试验研究[J].岩土力学,2012,33(12):3561-3569.
[7]梁忠雨,高峰,蔺金太,等.单轴下岩石声发射参数的分形特征[J].力学与实践,2009,32(1):43-46.
[8]高峰,李建军,李肖音,等.岩石声发射特征的分形分析[J].武汉理工大学学报,2005,27(7):67-69.
[9]李元辉,刘建坡,赵兴东,等.岩石破裂过程中的声发射b值及分形特征研究[J].岩土力学,2009,30(9):2559-2574.
[10]李博,孙强,王思源,等.单轴加载下砂岩声发射特征的试验分析[J].地质工程学报,2013,35(1):114-118.
[11]GRASSBERGER P,PROCACCIA I.Measuring the strange ness of strange attractor[J].Physical D,1983(9):198-208.
[12]沈忠,付小敏,黄兴建,等.软岩声发射序列的分形特征研究[J].中国测试,2016,42(6):9-13.
[13]徐志斌,谢和平.断裂尺度的分形分布与其损伤演化的关系[J].地质力学学报,2004,10(3):268-275.
[14]尹贤刚,李庶林,唐海燕.岩石破坏声发射强度分形特征研究[J].岩石力学与工程学报,2005,24(19):3512-3516.
(编辑:李妮)
Study on acoustic emission and fractal characteristics of sandstone under uniaxial compression
ZHANG Xin,FU Xiaomin,SHEN Zhong,HUANG Xingjian
(State Key Laboratory of Geohazard Prevention and Geoenvironment Protection,Chengdu University of Technology,Chengdu 610059,China)
In order to study the acoustic emission(AE)and fractal characteristics of sandstone under uniaxial compression,AE test under uniaxial compression was carried out for the early Paleozoic Silurian system sandstone of Xiaoheba group(S1x)on MTS815 program-controlled servo rigidity testing machine.The losing stability failure process was also analyzed for whole rock according to AE characteristic parameters,stress strain relation and fractal characteristics.The results show that the Xiaoheba sandstone group of AE and fractal characteristics and mechanical properties in the rock damage rupture process are consistent,and the stress ratio between 0.6 to 0.8 cumulative ring count rate trend as rock instability and failure identification method;phase space dimension selection on the correlation dimension has certain effect,with the increase of phase space of dimension(m),correlation dimension(D)showing increase stability-divergence in the development process;AE sequence in the stress ratio of 0.3 to 0.5,the correlation dimension(D)maximum;the correlation dimension curve of AE sequence for a evolution model of“fluctuation rising declining volatility”,at higher stress ratio of 0.7 to 0.8,the correlation dimension(D)fluctuated in a small range from 0.9 to 1.4.Therefore,it can provide a theoretical basis and data support for the monitoring and forecasting of rock mass instability and failure in engineering.
uniaxial compression;acoustic emission of sandstones;ringing counts rate;fractal;correlation dimension
A
:1674-5124(2017)02-0013-07
10.11857/j.issn.1674-5124.2017.02.003
2016-09-07;
:2016-10-09
国家自然科学基金项目(41272321)
张 昕(1992-),男,河南驻马店市人,硕士研究生,专业方向为岩土工程。
付小敏(1963-),女,四川绵阳市人,研究员,主要从事岩石室内试验相关工作。

