一种弹体初始挂装姿态测量新方法
张虎龙
(中国飞行试验研究院,陕西 西安 710089)
一种弹体初始挂装姿态测量新方法
张虎龙
(中国飞行试验研究院,陕西 西安 710089)
在弹体挂装试飞试验科目中,需要地面静态标定挂装弹体的姿态。针对挂装弹体无等高基准孔位的情况,提出一种基于旋转矩阵分解的计算方法。该方法只要求测量弹体的基本几何特征,综合采用特征探测算法、空间基准对齐算法、奇异值分解算法进行处理计算;为保证姿态测量参数的精度,要求在弹体粘贴辅助圆形标志时,分布要均匀,数量适中,提高空间基准对齐算法的稳健性。通过试验分析,在无等高基准孔位的情况下,旋转矩阵分解法能够实现姿态测量参数误差小于0.3°,方法切实有效,结果准确可靠,满足飞行试验的精度要求。
弹体;姿态测量;旋转矩阵;分解
0 引 言
挂弹飞行试验前,在地面往往需要对导弹的惯导相对机体主惯导的位姿关系进行高精度的标定,标定结果将作为两者的初始安装误差,用于机动飞行时惯导基准传递的修正值。在工程中,导弹惯导相对机体主惯导的位姿关系可由弹体挂装后在飞机基准下的位姿关系表达[1]。弹体挂装姿态测量常用的方法是挂装前,要求设计单位对弹体的水平和垂直等高点进行高精度标定[2];挂装后,利用三维坐标测量设备对弹体等高点进行测量,计算挂装姿态角度。但在实际工作中,由于设计单位提供的弹体几何特征不包括等高点,上述方法则会失效。针对此种情况,本文提出了一种新的姿态测量方法——旋转矩阵分解法,其基本原理是基于弹体已有的几何特征参数,建立弹体坐标基准;然后,利用三维坐标测量设备测量弹体几何特征在机体坐标基准下的特征参数;基于弹体特征的两套参数,建立弹体坐标基准与机体坐标基准的空间转换关系,计算旋转矩阵;对旋转矩阵进行分解,获取弹体的挂装姿态角。
1 系统设计及原理
1.1 系统设计
弹体测姿系统主要由全站仪、影像测量设备、工作站及其相应附件组成,如图1所示。
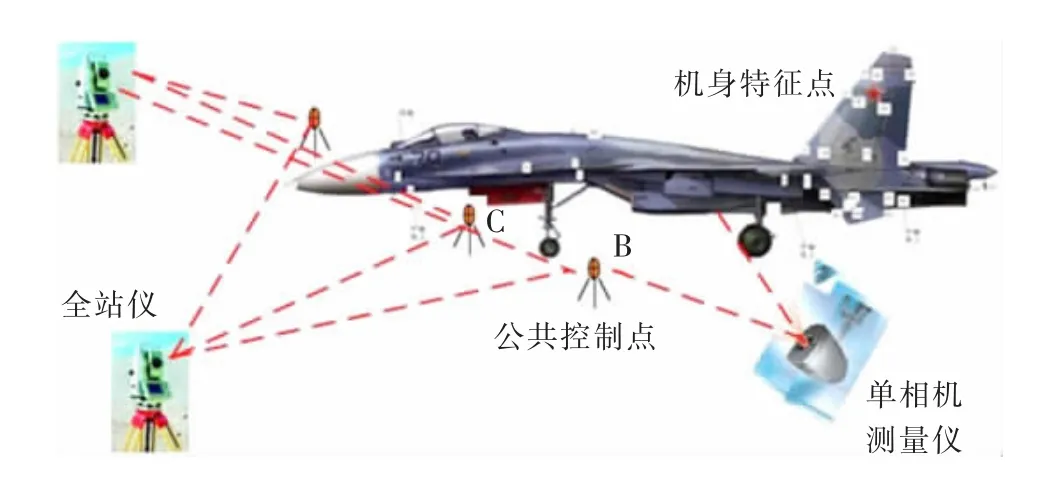
图1 测量现场示意图
1)全站仪:构建飞机机体坐标系,建立机体坐标基准并测量弹体附加标志。
2)单相机测量仪:测量弹体特征及附加标志,建立弹体坐标基准。
3)工作站:主要用于数据的实时数据处理与分析。
1.2 测量原理
1.2.1 坐标系与姿态角参数定义
在弹体测量过程中,需要建立两种空间坐标系:
1)弹体坐标系:以弹的质心为原点,弹体纵轴为Zb轴,在弹的水平面内,垂直Z轴向右为Xb轴,按右手定则确定Yb轴,如图2,坐标系O-XbYbZb。
2)机体坐标系:以飞机的质心为原点,飞机纵轴为Z轴,在飞机的水平面内,垂直Z轴向右为X轴,按右手定则确定Y轴,如图2,坐标系O-XYZ。
弹体挂装姿态参数[3](见图2)定义如下:
1)偏航角α:Xb轴在XZ坐标面上的投影与X轴的夹角。
2)俯仰角ω:Xb轴与XZ坐标面之间的夹角。
3)横滚角κ:Y轴在YbZb坐标面上的投影与Yb轴的夹角。

图2 姿态定义示意图

图3 机体坐标系建立示意图
1.2.2 机体坐标系与弹体坐标系建立
1)机体坐标系建立
为了建立高精度的机体坐标基准,采用基于测角的空间交会的方法进行[4]。
利用空间交会法测量飞机纵轴上两点A和B,如图3所示。计算矢量BA在设备坐标系 (黑色部分)下的方位角θ,然后,将设备坐标系方位零位旋转至矢量BA方向,原点定于纵轴点A或B[5]。
2)弹体坐标系建立
利用相机结合测量杆的摄影测量方法[6],探测弹体的圆柱面和吊挂面[7],基于3-2-1坐标系法构造弹体坐标系[8]。将圆柱面的对称轴作为弹体的X轴,吊挂面的法向作为Y轴,利用右手定则确定Z轴。
①圆柱面探测算法
圆柱面上的任意一点Pi(xi,yi,zi)到轴线的距离都为半径R。若中心轴线方向向量为(a,b,c),轴线上起始点为P0(x0,y0,z0),则实测半径:


误差方程为

其中ν为坐标观测值残差,引入两个约束条件:

式(3)中x0,y0,z0为利用圆柱面上点计算的重心坐标值,由式(3)、式(4)和式(5),按照最小二乘法进行约束平差,得到圆柱面参数。
②平面探测算法
平面的一般数学表达式为Ax+By+Cz+D=0(C≠0),参数表达式为x=xi+at;y=yi+bt;z=zi+ct;把参数表达式带入一般表达式中,得到t=a1xi-b1yi-c1zi-d1;若观测n个测量点,使n个测量点到平面的距离平方和最小的 a1,b1,c1,d1,即是所要求的平面参数[9]。 建立误差方程ν=AX,然后对ATA进行奇异值分解,最小奇异值对应的奇异值向量即是法向量(a,b,c),则平面方程为

1.2.3 旋转矩阵分解法
对于机体坐标系,若依次绕Y轴旋转α,再绕X轴旋转ω,绕Z轴旋转κ,即可实现飞机机体坐标系向弹体坐标系的坐标系对齐[10];反之,若利用对齐算法建立转换关系,可间接反求3个姿态角;其中,各角度旋转正方向定义为从坐标系原点沿各轴正向观察时逆时针旋转方向。
对齐算法模型采用三维赫尔墨特法,间接反求旋转矩阵[11]。由旋转矩阵分解出弹体的挂装姿态参数α,ω,κ,分解法具体实现如式(7)、式(8)。
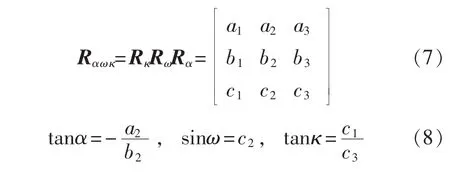
2 试验验证
本次试验的被测对象为挂装的气象传感器,传感器上有等高点(基准孔位),并粘贴圆形标志,分别采用常规计算方法与旋转矩阵分解法计算传感器挂装姿态,分析对比验证旋转矩阵计算法的有效性。
2.1 测量过程
1)利用全站仪建立机体坐标基准,并测量传感器已标定的等高点。
2)利用相机测量设备,采用圆柱面探测法与平面探测法,构建传感器坐标系;高精度测量传感器上粘贴的圆形标志点,获取其在传感器坐标系下的坐标值。
3)同样,利用全站仪依次测量粘贴的圆形标志点,获取其在传感器坐标系下的坐标值。
2.2 计算方法
1)常规计算法
利用表1数据,采用常规测量方法[8]进行计算,结果如下:

2)旋转矩阵分解法
利用表2数据,采用三维赫尔墨特法计算旋转矩阵为

按照式(7)和式(8)分解计算姿态角

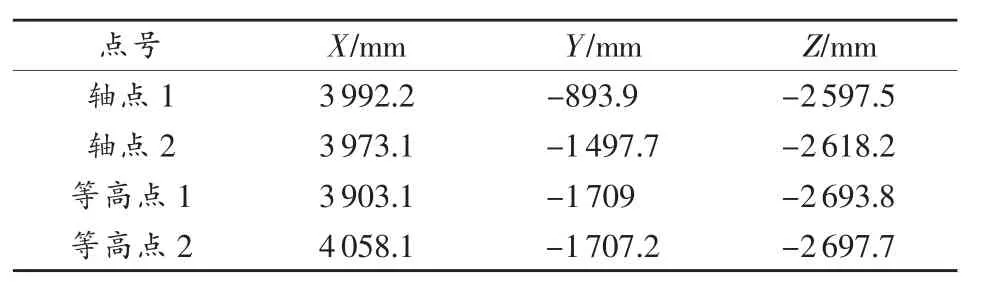
表1 基准孔位坐标
3)误差分析
矩阵分解法的误差主要体现在两个方面:传感器坐标系的构建误差和旋转矩阵的计算误差。
以基准孔位建立的坐标系为标准,检核探测法建立的坐标系误差。利用表1与表3中4组对应点数据,对X,Y,Z 3个方向分别求取中误差为(0.25,0.13, 0.11),综合误差
利用三维赫尔墨法反算的旋转矩阵计算标志点的设备坐标值,将其与实测坐标值作差,如表4所示,误差小于0.2mm,计算方法同M构。
结合该案例分析,矩阵分解法引起的点位误差约为0.2+0.3=0.5(mm);从常规测量方法与旋转矩阵分解法的计算结果对比可以看出,由点位误差引起的偏航角误差Δα=αch-αx=13′26″,俯仰角误差Δω=ωchωx=4′,横滚角误差Δκ=κch-κx=15′44″。该案例中传感器尺寸与日常测试任务中挂装弹体尺寸相当,因此,在弹体挂装试验中,采用矩阵分解法,姿态角误差小于0.3°。

表2 圆形标志点坐标

表3 探测法测量基准孔位坐标

表4 基于旋转矩阵的坐标反算值与实测值对比
3 结束语
弹体初始挂装姿态测量是挂弹试飞前必做的一项地面标定工作。本文结合工作实际,针对弹体无基准孔位的情况下,提出了一种基于旋转矩阵分解弹体姿态参数的计算方法,分析表明:1)矩阵分解法是基于弹体坐标系与机体坐标系的空间转换关系进行间接求取,现场作业具有较强的灵活性;2)传感器坐标系的构建误差直接影响矩阵分解法的最终误差,因此,在测量时,需做好坐标系的构建工作,特别是圆形标志点的空间布局要均匀,且具有一定的密度;3)为提高精度,在测量辅助圆形标志时,应使用单相机加编码点测量法,交会角度在60°~100°之间;4)矩阵分解法姿态角度误差小于0.3°,测试方法正确有效,满足飞行试验的精度要求。
[1]郑辛,武少伟,吴亮华.导弹武器惯导系统传递对准技术综述[J].导航定位与授时,2016,3(1):1-7.
[2]张虎龙,李娟妮.机载火控雷达天线阵面安装误差的高精度校准方法[J].现代电子技术,2011,34(19):4-8.
[3]张力军,张士峰,杨华波.基于欧拉角观测模型的航天器姿态确定方法[J].国防科技大学学报,2012,34(6):84-88.
[4]惠广裕,武瑞娟.利用双经纬仪高精度标定机载雷达天线阵面[J].地理空间信息,2015,13(3):36-38.
[5]武瑞娟,左泽敏,冀芳.一种飞机结构变形测量的新方法[J].科学技术与工程,2015,15(7):265-269.
[6]何红丽,陈茜,赵静.一种高精度飞机形变测量方法[J].测控技术,2014,33(4):16-18.
[7]谭昌柏.逆向工程中基于特征的实体模型重建关键技术研究[D].南京:南京航空航天大学,2006.
[8]王丽秀.飞机柔性装配制孔设备的工件坐标系建立方法[J].机械设计与制造,2012(4):229-231.
[9]侯海啸,惠广裕,吴衡.飞行试验机体受载变形静态检测技术[J].测控技术,2011,30(1):149-152.
[10]冯文灏.近景摄影测量[M].武汉:武汉大学出版社,2002:59-71.
[11]李国栋,赵威,田国会.一种基于旋转矩阵分解的视觉伺服控制算法[J].山东大学学报,2012,42(1):45-49.
(编辑:李刚)
A new method for measuring the pose of projectile body in initial hanging
ZHANG Hulong
(Chinese Flight Test Establishment,Xi’an 710089,China)
In the missile body flight subjects hanging test,the pose of the missile body needs to be calibrated on the ground.Under the condition of no same high datum hole,a method based on the decomposition of the rotation matrix is proposed.The method only requires the measurement of the basic geometric characteristics of the projectile;the feature detection algorithm,the spatial datum alignment algorithm,and the singular value decomposition algorithm are used comprehensively to deal with the computation;through experimental analysis,the rotation matrix decomposition method can achieve pose parameter accuracy above 0.3°under the condition of no same high datum hole. In order to ensure the accuracy of measurement of pose parameters,the method requires auxiliary circle mark pasted in the projectile,even distribution,moderate number,and improves the robustness of the spatial reference alignment algorithm.The actual test proves that the method is effective,accurate and reliable and fully meets the precision requirements of such tests.
projectile;pose measurement;rotation matrix;decomposition
A
:1674-5124(2017)02-0025-04
10.11857/j.issn.1674-5124.2017.02.005
2016-07-20;
:2016-09-05
张虎龙(1979-),男,湖南岳阳市人,高级工程师,研究方向为光电测试、信息融合、目标跟踪技术等。

