孔洞缺陷位置对灰岩力学特性影响的数值模拟研究

吴 亮，刘 帅,刘安芳，王廷超，王子睿

(1.云南省滇中引水工程有限公司，云南 昆明 650000；2.华北水利水电大学 地球科学与工程学院，河南 郑州 450046；3.云南省滇中引水工程建设管理局，云南 昆明 650000)

由于岩溶、风化等地质作用，灰岩岩体中存在各种节理、孔洞等缺陷，这使得岩体强度与变形表现出强烈的不连续性、非均匀性和各向异性[1-3]，也对边坡、隧道等相关工程的围岩稳定性产生严重的威胁[4-5]。其中孔洞缺陷在岩体中分布位置不同，势必对岩体的力学性质产生直接影响，因此，开展孔洞缺陷位置对灰岩力学特性影响的研究，对于灰岩地区工程岩体的围岩控制和加固支护等方面具有一定指导意义。

目前孔洞缺陷影响岩体力学性质的研究多集中在孔洞形状[6]、孔洞大小[7]、孔洞数量[8]以及孔洞与其他缺陷相结合方面[9]，常用的研究方法主要为室内试验和数值模拟等方法[10-11]。虽然部分学者对孔洞缺陷的研究考虑了孔洞分布的影响因素，然而大多是基于多个孔洞进行排列组合而进行的研究，较少涉及单个孔洞的不同位置对岩体力学性质的影响。开展只考虑单个孔洞位置为唯一变量的研究，能更好地揭示不同孔洞缺陷位置下岩体变形破坏的变化规律。本文以不同位置含有单个圆形孔洞的灰岩岩体为研究对象，利用PFC2D对其进行数值模拟，来探讨孔洞缺陷位置对灰岩力学特性的影响。

1 灰岩宏-细观参数标定

相较于宏观室内试验，PFC2D软件适用于分析岩石渐进破坏过程中的细观特征，如裂纹演化、应力集中区域等，是目前岩石力学领域非常可靠的数值模拟方法[12]。进行数值模拟试验之前，需要利用PFC程序中的平行黏结模型构建与室内试验岩样相同的完整模型进行数值模拟试验，并进行对比，满足室内试验和数值模拟结果的一致性[13-14]。首先对岩样进行室内试验，测定致密新鲜灰岩的物理力学参数。其中单轴抗压强度试验采用TAW-2000微机控制的岩石三轴试验系统进行，单轴抗压试验高径比为21(100 mm×φ50 mm)的标准圆柱岩样，采用0.001 mm/s的变形控制加载。灰岩完整岩样数值模型如图1所示。

图1 灰岩完整岩样数值模型

与室内试验采用相同的试验方法和加载条件，对PFC2D程序中得出应力应变曲线进行校核，进而得到适用于PFC2D模拟的细观参数，如表1所示。室内试验与数值试验得到的岩样模型破坏形态和单轴应力-应变曲线如图2所示。可以看出，试验试样和数值试样的峰值强度和变形模量均基本一致，且两者的破坏形态相似，表明PFC2D模型的细观参数满足试验要求。

(a)破坏形态对比 (b)应力-应变曲线对比

表1 用于PFC2D数值模拟灰岩的部分细观参数

2 数值模拟方案

为研究孔洞位置对灰岩力学特性的影响，在已标定完整参数的数值模型基础上，建立相同孔洞但孔洞位置不同的缺陷岩体模型。模型内含有单个孔洞，设置孔洞形状为圆形，孔径为10 mm。建立模型基于标准圆柱形岩样，为轴对称模型，所以仅在模型内第一象限区域内布置不同位置，建立的各个数值模型如图3所示。其中：孔位一模型中圆孔圆心位于模型中心(坐标原点)；孔位二模型中圆孔相对孔位一向右平移12.5 mm，位于模型右侧中间；孔位三模型中圆孔圆心位于45°角平分线上，且距离模型中心约为17.68 mm；孔位四位于模型上半段中心，圆孔圆心距离模型中心为25 mm。

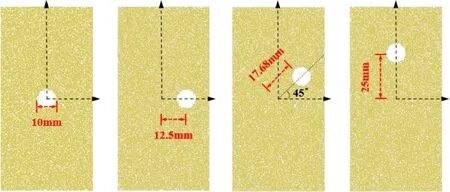
(a)孔位一 (b)孔位二 (c)孔位三 (d)孔位四

模型建立后分别进行模拟单轴压缩试验，监测试验过程中各模型的应力应变、裂纹发育及位移场的变化特征，加载方式和条件与完整岩样相同。

3 模拟试验结果分析

3.1 各模型应力应变分析

导出各模型的应力应变数据并进行计算，得到各模型的应力-应变曲线如图4所示，各模型的单轴抗压强度和弹性模量值如表2所示。

由图4和表2可以看出，各模型中完整模型的单轴抗压强度和弹性模量最大，分别为110.69 MPa和73.05 GPa。说明圆孔缺陷的存在，无论处于模型内什么位置，都会降低岩样的单轴抗压强度和弹性模量。孔位一模型至孔位四模型的单轴抗压强度分别为94.12 MPa、83.32 MPa、80.68 MPa和82.17 MPa，以圆形孔洞位于模型中心时其单轴抗压强度相对最大；孔洞位于模型右半侧中心和上段中心时，其抗压强度大致相当，以孔位二模型的单轴抗压强度稍大；圆形孔洞位于45°角平分线时，单轴抗压强度最小。相较于完整模型，孔位一模型的单轴抗压强度下降了约14.97%，而孔位三模型的单轴抗压强度下降了约27.11%。说明在模型中孔洞处在不同位置，会影响岩样单轴抗压强度的变化。

图4 各模型应力应变曲线

表2 各模型单轴抗压强度和弹性模量

从图4中也可以看出，各个含单个圆孔缺陷模型在峰值应力前，其应力-应变曲线基本是重合的，结合表2中不同孔洞位置模型的弹性模量值，孔位一模型至孔位四模型的弹性模量分别为68.78 GPa、68.47 GPa、68.51 GPa和68.69 GPa,弹性模量的变化量很小，说明在含圆孔的各模型的缺陷面积相同条件下，孔洞位置的变化对岩样弹性模量的影响不大。

3.2 裂纹分布特征

为展现各个模型内裂纹演化的大致过程，分别在峰值应力前后和峰值应力时的加载条件下，对各模型的裂纹分布特征进行监测。峰前阶段取50%峰值应力的应力水平，峰后阶段为降低到70%峰值应力的应力水平。各模型的裂纹演化特征如图5所示，其中，红色裂纹代表拉伸裂纹，黑色裂纹代表剪切裂纹。

从图5中可以看出，完整模型在一半峰值应力水平时，模型内开始出现分散的拉伸裂纹，至峰值应力时，开始出现一定数量的剪切裂纹，虽然裂纹已经贯通模型，但拉伸裂纹和剪切裂纹在模型内分布仍相对分散。在峰前50%峰值应力时，各个含有圆孔模型中，裂纹主要集中在圆孔附近，并且在圆孔上下顶点处裂纹扩展程度较高；说明此阶段裂纹发育随着圆孔位置不同而向孔洞处转移。在峰值应力时，含孔洞模型中的裂纹发育已基本贯通整个模型，但随着孔洞位置的不同，裂纹贯通的位置和形态不一，孔位一模型中主要以孔洞为中心，沿着模型对角线方向分布。孔位二模型中随着孔洞位置变化，而使贯通裂纹移向模型右侧。孔位三模型中裂纹主要集中在模型右上侧，孔位四模型中裂纹集中在模型的上半段。至峰后破坏阶段，含孔洞缺陷不同位置的各个模型中的裂纹继续沿着峰值应力时的裂纹发育扩展，致使模型完全破坏。

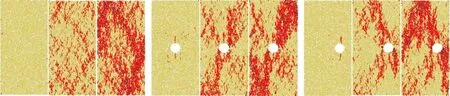
(a)完整模型 (b)孔位一模型 (c)孔位二模型

(d)孔位三模型 (e)孔位四模型

通过以上分析，孔洞位置对模型内裂纹的发育有直接影响，孔洞的存在使裂纹萌生较早，且主要集中在圆孔附近，使模型破坏后裂纹贯通和分布形态发生改变，贯通裂纹向孔洞位置方向发生转移，进而影响模型的破坏路径。

3.3 各模型破坏后位移场分析

在峰后阶段应力水平降低到0.7倍的抗压强度时，分析各模型的位移场分布特征，对比各模型在孔洞位置影响下的破坏形态变化。各模型的位移场分布如图6所示。

(a)完整模型 (b)孔位一模型 (c)孔位二模型 (d)孔位三模型 (e)孔位四模型

与图5中峰后阶段裂纹演化特征一致，各模型的位移场分布受圆孔位置的影响。完整模型最大位移发生在模型右侧中间，并在此处斜向上和向下发生主劈裂破坏。孔位一模型沿模型对角线发生劈裂破坏，最大位移处在模型右上侧处。孔位二模型孔洞靠近模型右侧，沿着孔洞其右上侧为主要破坏位置。孔位三模型的破坏形态与孔位二模型相似，但主破坏区域小于孔位二模型。孔位四模型受孔洞位置上移影响，其最大位移区域发生在模型左上侧，这一区域较其他模型破坏更剧烈。

4 结论

基于完整灰岩岩样的室内试验，利用PFC2D数值模拟方法建立不同孔洞位置的数值模型进行单轴压缩试验，通过分析各模型的应力应变、裂纹分布和模型破坏后位移场分布特征，得出如下结论：

(1)圆形孔洞缺陷的存在会劣化岩样的力学性质，使岩样的单轴抗压强度和弹性模量降低。孔洞位置对岩样的单轴抗压强度有较大影响，以圆形孔洞位于45°角平分线时岩样的单轴抗压强度最小，单轴抗压强度较完整模型下降了约27.11%。在孔洞缺陷大小相同条件下，孔洞位置对岩样的弹性模量影响不大。

(2)孔洞位置影响模型的裂纹演化特征，使裂纹萌生时主要集中在圆孔缺陷附近，并使模型破坏后裂纹的贯通和分布形态发生改变，贯通裂纹向孔洞位置方向发生转移。

(3)孔洞位置不同造成岩样主要破坏路径不同，各模型基本沿着圆孔位置发生劈裂破坏，使岩样的破坏形态发生改变，影响模型位移场的分布特征。