磁通量压缩发生器电枢的动力学特性仿真计算研究
鲁峰, 陈朗, 冯长根, 王立华
(1.中国水产科学研究院 渔业工程研究所, 北京 100141; 2.北京理工大学 机电学院, 北京 100081)
磁通量压缩发生器电枢的动力学特性仿真计算研究
鲁峰1,2, 陈朗2, 冯长根2, 王立华1
(1.中国水产科学研究院 渔业工程研究所, 北京 100141; 2.北京理工大学 机电学院, 北京 100081)
为了有效地提高磁通量压缩发生器的输出性能,设计了一种柱锥形结构的磁通量压缩发生器,研究了发生器结构的动力学响应特性。采用聚类算法和文本挖掘技术对非线性动力学仿真软件LS-DYNA进行了二次开发,编制了节点随机失效和有限元网格自动分离程序,建立了一个仿真模型,实现了对发生器的动态膨胀和断裂过程的数值仿真计算。给出了发生器电枢的膨胀角、径向膨胀速度及断裂半径等重要参数的变化。计算结果表明,该模型可以较好地预测电枢发生断裂的时间和位置,且计算得到的电枢膨胀角、径向膨胀速度和断裂半径与理论计算结果较为接近。
兵器科学与技术; 磁通量压缩发生器; 电枢; 断裂半径
0 引言
磁通量压缩发生器是通过炸药爆炸驱动金属电枢膨胀继而压缩磁场的方法,将炸药的化学能转化为电磁能的强脉冲能源装置,主要用于电磁脉冲武器的初级能源。磁通量压缩发生器的电感和电阻的动态变化主要取决于电枢的膨胀,对电枢膨胀的动力学特性进行描述是设计磁通量压缩发生器的首要工作。电枢在内爆载荷作用下的膨胀和断裂过程是磁通量压缩发生器设计时的重要依据,对发生器的输出性能起着关键性作用。采用数值模拟方法,研究炸药爆轰驱动下磁通量压缩发生器中电枢的动力学响应特性,对改善和提高发生器的性能有着重要意义。
国内外学者分别从理论、数值模拟和实验方面对磁通量压缩发生器中的电枢膨胀运动开展了相关研究工作。晏成立等[1]进行了炸药驱动电枢膨胀的实验研究,分析了电枢的膨胀角变化情况。Neuber等[2]对电枢与定子的接触进行了数值模拟,计算了电枢的径向位移和接触点的轴向速度,结果表明电枢向定子移动的轴向和径向速度相同。杨显俊等[3]对炸药驱动电枢进行了二维动力学模拟计算,分析了电枢膨胀速度及膨胀角随径向位置的变化情况。马月芬等[4]以解耦的磁压缩发生器运行模型为研究对象,建立了磁通损耗和电阻损耗的耦合因子解析式。孙奇志等[5]建立了电枢的一维爆轰驱动模型,对电枢运行的物理过程进行了系统描述。何勇等[6]对螺旋形磁通压缩发生器的电枢膨胀过程进行了数值模拟,给出了电枢膨胀角与电枢材料、电枢几何尺寸和线圈尺寸的关系。赵继波等[7]对炸药内爆驱动电枢过程进行了一维磁流体力学模拟计算,分析了空腔磁场向压缩电枢中的磁扩散现象,计算了电枢内壁的速度历程曲线。谷卓伟等[8]针对电枢套筒运行的物理过程开展了一维爆轰磁流体动力学数值模拟,得到了套筒运动位移曲线及冲击加载下套筒表面的压力历史。畅里华等[9]扫描超高速光电摄影系统,观察到电枢套筒内爆的整个压缩过程,获得了直径随时间变化曲线及压缩速度。Wang等[10]采用爆轰波速度和电枢膨胀角两个参数来描述电枢的膨胀动力学响应,并将其应用于发生器的电感计算中。Xu等[11]采用薄壳模型代码和有限元分析方法,建立了优化定子线圈设计的模型,该模型可提高发生器的输出性能。章征伟等[12]采用材料强度的零维不可压缩模型对铝金属管的内爆过程进行了模拟,分析了材料强度对电磁驱动金属管内爆过程的影响。
本文设计了一种柱锥型电枢的磁通量压缩发生器,建立了三维有限元仿真模型,采用非线性动力学有限元法计算了电枢的膨胀角、径向膨胀速度,并与理论计算结果进行了对比。针对目前研究现状,对电枢的膨胀断裂过程主要是通过网格删除的方法来实现,并不能有效地模拟电枢的断裂过程,因此本文采用网格分离和节点随机失效的方法实现了电枢及螺线管的断裂,给出了电枢的断裂半径。
1 计算模型
图1为柱锥型磁通量压缩发生器的三维计算模型图。发生器工作时,由雷管点火引爆起爆药,继而引爆高能炸药。电枢在管内炸药爆轰产物压力的驱动下膨胀,依次与螺线管各匝线圈相接触,从而压缩电枢与螺线管之间的磁通量,减小回路电感,放大负载端的电流。其中炸药和电枢使用ANSYS前处理软件进行建模和网格划分。螺线管采用Pro/Engineer软件进行建模,建模完毕后将其导入到ANSYS中进行网格划分。由于螺线管不具对称性,建模时采用全模型。起爆药、炸药、电枢和和螺线管均采用拉格朗日算法。模型中,起爆药药柱直径为2.3 cm,长度为1.5 cm. 炸药和电枢的结构分别由柱型部分和锥形部分组成,锥形部分的锥角为8°. 炸药柱型部分直径为2.0 cm,长为24.5 cm;锥形部分底面直径为4.45 cm,长为8.22 cm. 电枢柱型部分的外径为2.4 cm,长为24 cm;柱锥形部分底面外径为4.75 cm,长为8.72 cm. 电枢外部的螺线管采用变螺距设计,螺距分为4段,每段采用固定螺距,分别为3.5 mm、5.0 mm、6.0 mm和7.0 mm. 其中,第4段内径比前3段大0.2 cm,第4段螺线管的起始端与电枢的柱锥部分结合缝对齐。螺线管截面直径为0.2 mm. 模型中,将起爆药前端面的中心点设置为起爆点,以替代雷管的作用。

图1 柱锥型磁通量压缩发生器的三维计算模型图Fig.1 Three-dimensional model of cylinder-conical magnetic flux compression generator
发生器的起爆药采用TNT炸药,其爆轰产物采用JWL状态方程描述。(1)式为JWL状态方程[13],表1给出了TNT的JWL状态方程参数。电枢内部的炸药采用PBXN-5炸药,采用点火增长反应模型对其进行描述。(2)式为点火增长反应模型公式[14],表2给出了PBXN-5炸药的点火增长反应模型参数。电枢和螺线管的材料为纯铜,采用塑性动力学材料模型进行描述。
(1)
式中:p为爆轰产物压力;V为爆轰产物的相对比容;E为能量密度;A、B、R1、R2和ω为实验标定参数。
(2)
式中:λ为炸药反应度;t为时间;ρ为密度;ρ0为初始密度;I,G1、G2、a、b、x、c、d、y、e、g和z为实验标定的常数。

表1 TNT炸药JWL状态方程参数

表2 PBXN-5炸药点火增长反应模型参数
为了模拟电枢爆炸过程中的动态膨胀断裂过程,本文采用预设壳体单元破片的方法,编制应用程序对后台计算文本文件进行数据挖掘,采用聚类算法对新生成具有相同坐标的节点进行聚类,并写入到计算文件的相应位置中,从而实现电枢和螺线管网格节点的分离,使每个网格成为一个独立单元。将具有相同坐标的壳体单元节点组成一个节点组,节点的失效应变由程序自动生成并写入计算文件。实验表明,柱形壳体内爆形成的破片符合Mott分布[15],故失效应变为服从Mott分布的随机数,本文采用程序模拟Mott分布函数。当金属管爆炸膨胀达到失效应变时,相邻两个壳体单元的节点则会分离,产生断裂的效果。
2 计算结果与分析
2.1 电枢的运动过程及爆轰波的传播
图2为发生器运行的不同时刻下(0 μs、10 μs、20 μs、30 μs、40 μs)计算得到的电枢膨胀过程和爆轰波传播过程。由图2可知,发生器的运行时间约为40 μs,磁压缩过程的时间约为30 μs. 0 μs时起爆药爆炸,随后引爆主炸药,爆轰波开始在主炸药内部传播,波阵面后的金属壳体在爆轰产物作用下,沿内表面产生塑性变形,并迅速向外膨胀,使得金属管与螺线圈之间的环形空间中的磁通量受到压缩。10 μs时,波阵面传播至螺线圈所包围炸药区域,使金属管与螺线圈之间的环形空间中的磁通量开始受到压缩。30 μs时,电枢与第1匝线圈接触。40 μs时,波阵面传播至炸药另一端,磁压缩过程也基本结束。值得注意的是,当波阵面传至锥形区时,随着电枢的膨胀,螺线圈与电枢间的空间迅速减小,从而加快了电感的下降速度。
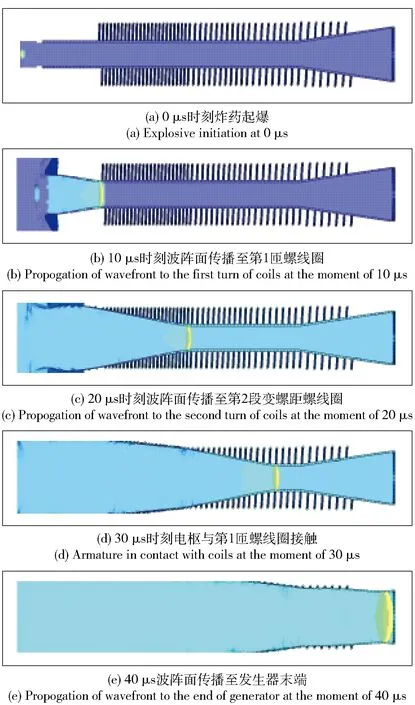
图2 发生器运行在不同时刻下电枢的膨胀及爆轰波的传播过程Fig.2 Armature expansion and propagating process of detonation wave at different operating times (t=0 μs, 10 μs,20 μs, 30 μs, 40 μs) of generator
2.2 电枢膨胀角
电枢的膨胀角是磁通量压缩发生器的一项重要参数。电枢的膨胀角可以用Gurney公式来计算。利用Gurney公式可以计算出爆炸驱动金属管运动的径向膨胀速度和膨胀角。对于圆柱壳体,Gurney公式[16]为
(3)

(4)
(5)
式中:ρe和ρa分别为炸药和电枢的密度;Re和Ra分别为炸药和电枢的半径;L为长度。求得破片速度后,再用(6)式计算金属管的膨胀角:
(6)
式中:α为金属管膨胀角;D为炸药爆速。
表3给出了发生器的规格参数,根据(3)式~(6)式计算出电枢的膨胀角为11.7°. 数值模拟中,当爆轰波阵面传播至离起爆端约24 cm的位置时,电枢膨胀角为9.6°.

表3 磁通量压缩发生器的材料参数
2.3 电枢的径向膨胀速度
电枢爆炸膨胀的径向膨胀速度u与其膨胀角α有关,可由(7)式直接求得
u=Dtanα.
(7)
依据(7)式可计算出电枢的径向膨胀速度为1 500 m/s. 计算中,沿爆轰波的传播方向,依次选取距起爆端8.2 cm、12.4 cm和16.6 cm位置的单元观察电枢的径向膨胀速度,图3给出各单元的径向膨胀速度随时间变化的曲线。由图3可见,当爆轰波刚好经过电枢管壁时,由于爆轰产物压力起主导作用,该处的管壁立刻具有一定的初速度和初位移。随着发生器的运行,爆轰产物压力不断减小,电枢的膨胀速度逐渐趋于平稳然后缓慢下降。当电枢膨胀至与螺线管接触时,其速度明显下降且变得不稳定。电枢推动螺线管继续膨胀到一定程度时,电枢和螺线管相继断裂并以破片的形式向四周扩散。3个单元的最大径向膨胀速度均为1 589 m/s,与理论计算值较为接近。
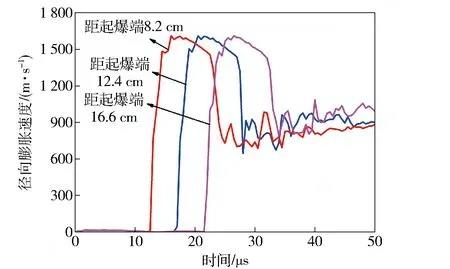
图3 电枢在不同位置处的径向膨胀速度Fig.3 Radial expansion velocities of armature at different locations
2.4 电枢断裂半径
若电枢在与螺线管接触前产生裂纹,意味着电枢圆周方向的电导率降为0,这严重影响了电枢表面的径向电流,使磁通量压缩发生器的输出性能大大降低。因此,在发生器设计中,要求电枢在与线圈接触前不能出现断裂现象。电枢材料一般选用延性较好的金属,其半径膨胀到初始半径的2~3倍时仍不会发生断裂,本文的发生器使用紫铜作为电枢材料。电枢的断裂半径可由(8)式来计算[16]:
(8)
式中:Rf为金属壳体断裂时的内径;R0为金属壳体的初始内径;Y为材料的屈服强度;γ为爆炸产物的多方指数,这里取γ=3. 初始爆炸气体压力由(9)式计算:
(9)
式中:ρ0为炸药初始密度;D为爆速。这样,由(7)式计算得到的电枢断裂半径为2.8 cm.
根据数值模拟的计算结果,电枢在爆炸产物驱动下迅速向外膨胀,当发生器运行至22.5 μs时,半径达到3.1 cm,此时壳体出现纵向裂纹,如图4所示。随着发生器的膨胀,裂纹不断扩展加宽直至电枢完全断裂。壳体膨胀至断裂后,爆轰产物通过裂缝向外释放,作用于壳体内表面的压力迅速下降,壳体随着裂纹的不断扩展最终完全断裂,形成破片向四周飞散,如图5所示。计算结果表明,发生器电枢的断裂半径为3.1 cm,略大于理论计算值,电枢在与相应位置的螺线管接触前并未出现任何裂纹,这表明本文所设计的磁通量压缩发生器符合设计要求。

图4 22.5 μs时刻电枢壳体出现裂纹Fig.4 The cracks appearing on the armature shell at the moment of 22.5 μs
2.5 柱锥形部分电枢的运动及膨胀角
电枢的末端为锥状,锥角为8°,略小于柱形部
分电枢的膨胀角9.6°. 数值计算结果表明,当爆轰波传至锥形段时,该段电枢的膨胀角为1.5°,因而膨胀后的形状接近于圆柱,如图6所示。由此可知,在第4段螺线管内的磁压缩过程结束之前,电枢并不会与各匝线圈发生接触。这样设计的好处是,在磁压缩发生器运行后期,加快电感的下降速度,从而增大电流的上升速度。
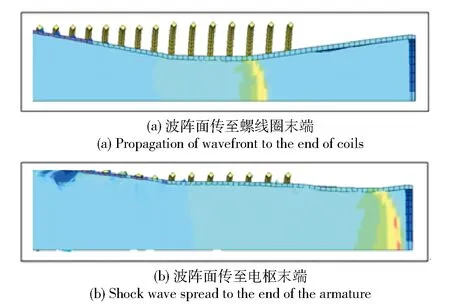
图6 计算得到的电枢锥形末端的膨胀过程Fig.6 Expansion process of conical end of armature
表4给出了电枢的膨胀角、径向膨胀速度及断裂半径的理论计算结果与数值模拟计算结果的对比关系,可见理论计算值与模拟计算值较为接近。由表4可知,电枢膨胀角的模拟结果比理论计算结果偏低,这主要是理论计算中并未考虑稀疏波对冲击波的影响所致。而电枢径向膨胀速度的模拟结果比理论计算结果偏高,主要是由于理论计算中没有考虑电枢受炸药驱动的影响。电枢断裂半径的模拟结果比理论计算结果偏高,主要是由于理论计算并未考虑材料的失效应变及力学性能不均匀性。

表4 理论计算结果与数值模拟计算结果的对比
3 结论
本文设计一种柱锥形磁通量压缩发生器,建立了发生器的三维有限元计算模型,并采用网格单元失效自动分离的方法,研究了发生器电枢的动力学响应特性。计算结果表明,柱形部分电枢的膨胀角为9.3°,锥形部分电枢的膨胀角为1.5°,电枢的最大径向膨胀速度为1 589 m/s. 锥形部分的电枢在膨胀过程中并不会依次与各匝线圈发生接触,从而加快了电感的下降速度,增大电流的上升速度。发生器电枢的断裂半径为3.1 cm,故电枢在与螺线管接触前并未出现任何裂纹,这表明本文所设计的磁通量压缩发生器符合设计要求。因此,本文所建立的数值模拟方法可有效地为磁通量压缩发生器的设计和改进提供重要依据,为后续的实验环节奠定良好的设计基础。
References)
[1] 晏成立, 于川, 李良忠, 等. 爆炸磁通量压缩发生器金属管爆炸试验研究[J]. 高压物理学报, 1999, 13(1): 76-80. YAN Cheng-li, YU Chuan, LI Liang-zhong, et al. Explosive bulge test for metal tube of magnetic flux compression generator (MFCG)[J]. Chinese Journal of High Pressure Physics, 1999, 13(1): 76-80. (in Chinese)
[2] Neuber A A, Dicken S J, Coenette J B, et al. Electricalbehavior of a simple helical flux compression generator for code benchmarking[J]. IEEE Transactions on Plasma Science, 2001, 29(4): 573-578.
[3] 杨显俊, 董志伟. 爆磁压缩发生器的爆炸管动力学效应[J]. 强激光与粒子束, 2007, 19(6): 889-892. YANG Xian-jun, DONG Zhi-wei. Dynamic effect of exploding tube in MFCG[J]. High Power Laser and Particle Beams, 2007, 19(6): 889-892. (in Chinese)
[4] 马月芬, 张庆明, 吴碧, 等. 爆磁压缩发生器的耦合损耗因子研究[J]. 兵工学报, 2009, 30(2): 80-83. MA Yue-fen, ZHANG Qing-ming, WU Bi, et al. Study on coupling loss factor of magnetic flux compression generator[J]. Acta Armamentarii, 2009, 30(2): 80-83. (in Chinese)
[5] 孙奇志, 孙承维. 轴线起爆式螺线管型爆磁压缩发生器理论模型[J]. 强激光与粒子束, 2009, 15(4): 385-390. SUN Qi-zhi, SUN Cheng-wei. Model of helical magnetic compression generators with explosive initiated axially[J]. High Power Laser and Particle Beams, 2009, 15(4): 385-390. (in Chinese)
[6] 何勇, 孔斌. 磁通压缩发生器数值模拟研究[J]. 南京理工大学学报, 2009, 33(5): 565-570. HE Yong, KONG Bin. Numerical simulation of magnetic flux compression generator[J]. Journal of Nanjing University of Science and Technology, 2009, 33(5): 565-570. (in Chinese)
[7] 赵继波, 孙承纬, 谷卓伟, 等.内爆圆柱套筒磁通量压缩的磁流体力学计算[J]. 强激光与粒子束, 2014, 26(9): 095003. ZHAO Ji-bo, SUN Cheng-wei, GU Zhuo-wei, et al. Magneto-hydrodynamic calculation of magnetic flux compression using imploding cylindrical liners[J]. High Power Laser and Particle Beams, 2014, 26(9): 095003. (in Chinese)
[8] 谷卓伟, 罗浩, 张恒第, 等. 炸药柱面内爆磁通量压缩实验技术研究[J]. 物理学报, 2013, 62(17): 170701. GU Zhuo-wei, LUO Hao,ZHANG Heng-di, et al. Experimental research on the technique of magnetic flux compression by explosive cylindrical implosion[J]. Acta Physica Sinica, 2013, 62(17): 170701. (in Chinese)
[9] 畅里华, 何徽, 温伟峰, 等. 炸药柱面内爆磁通量压缩超高速同时分幅/扫描摄影技术[J]. 强激光与粒子束, 2015, 27(11): 115002. CHANG Li-hua, HE Hui, WEN Wei-feng, et al. Ultrahigh-speed simultaneous framing and streak photograph of magnetic flux compression by explosive cylindrical implosion[J]. High Power Laserand Particle Beams, 2015, 27(11): 115002. (in Chinese)
[10] Wang Y, Zhang J, Chen D, et al. Fastmodeling of flux trapping cascaded explosively driven magnetic flux compression generators[J]. Review of Scientific Instruments, 2013, 84(1): 014703.
[11] Xu F, Ding W. High power pulse compression using magnetic flux compression[J]. Journal of Applied Physics, 2012, 111(9): 094508.
[12] 章征伟, 魏懿, 孙奇志, 等. 材料强度对电磁驱动固体套筒内爆过程的影响[J]. 强激光与粒子束, 2016, 28(4): 045017-1-5. ZHANG Zheng-wei, WEI Yi, SUN Qi-zhi, et al. Effect of material strength on electromagnetic driven solid liner implosion[J]. High Power Laser and Particle Beams, 2016, 28(4): 045017-1-5. (in Chinese)
[13] Kury J W, Hornig H C, Lee E L, et al. Metal acceleration by chemical explosives[C]∥Proceedings of the 4th Symposium (International) on Detonation. Arlington, VA, US: Office of Naval Research, 1965: 3-12.
[14] Lee E L, Tarver C M. Phenomenological model of shock initiation in heterogeneous explosives[J]. Physics of Fluids, 1980, 23(12): 2362-2372.
[15] Mott N F. Fragmentation of shell cases[J]. Proceedings of the Royal Society of London Series A-Mathematical and Physical Sciences, 1947, 189(1018): 300-308.
[16] 张宝平, 张庆明, 黄风雷. 爆轰物理学[M]. 北京: 兵器工业出版社, 2001: 305-320. ZHANG Bao-ping, ZHANG Qing-ming, HUANG Feng-lei. Detonation physics[M]. Beijing: Publishing House of Ordnance Industry, 2001: 305-320. (in Chinese)
Simulation of Dynamic Characteristics of Armature in Magnetic Flux Compression Generator
LU Feng1,2, CHEN Lang2, FENG Chang-gen2, WANG Li-hua1
(1.Fishery Engineering Research Institute, Chinese Academy of Fishery Sciences, Beijng 100141, China; 2.Beijing Institute of Technology, Beijng 100081, China)
In order to improve the performance of magnetic flux compression generator, a cylinder-conical generator is designed, and the dynamic response characteristic of armature in the generator is studied. The clustering algorithm and text mining technology are used to develop secondarily LS-DYNA software. The code which makes the node failure and separates the finite element mesh is compiled, and a simulation model is established to simulate dynamic expansion and fracture process of generator. Expansion angle, radial expansion velocity and fracture radius of armature are presented. The calculated results show that the proposed model can be used to predict the expansion and fracture process of armature, and the simulated expansion angle, radial expansion velocity and fracture radius of armature are close to the theoretical values. The method can be used for the design of the magnetic flux compression generator, optimizing the structure of generator and improving its output performance.
ordnance science and technology; magnetic flux compression generator; armature; fracture radius
2016-06-24
鲁峰(1984—),副研究员,博士。E-mail: insomnialf@163.com
TJ99
A
1000-1093(2017)02-0383-06
10.3969/j.issn.1000-1093.2017.02.024

