基于位移传感器阵列的卡膛几何参数测量方法
彭澎, 狄长安, 王哲军
(南京理工大学 机械工程学院, 江苏 南京 210094)
基于位移传感器阵列的卡膛几何参数测量方法
彭澎, 狄长安, 王哲军
(南京理工大学 机械工程学院, 江苏 南京 210094)
大口径火炮弹丸装填不到位及卡膛姿态的一致性分别会对火炮内膛磨损及射击精度产生较大影响。针对某型火炮弹丸卡膛状态参数测量现状,提出一种适用于射击现场的基于位移传感器阵列的卡膛几何参数测量方法。介绍了卡膛几何参数测量原理及组成,分别建立了药室轴线测量模型、弹丸轴线测量模型及弹丸尾端面等测量模型,并对各测量模块的性能进行了分析与验证;在此基础上,利用该测量装置对射击现场弹丸卡膛状态下的几何参数进行实际测量,通过分析实验结果验证了该测试系统测量的稳定性与准确性。
兵器科学与技术; 卡膛; 姿态测试; 坐标变换; 位移测量; 倾角
0 引言
大口径火炮通常采用弹、药分开装填,弹丸在人力或输弹机的作用下推入膛内,弹丸进入炮膛后靠惯性卡膛。弹丸的卡膛力及卡膛姿态的一致性是弹丸装填的重要参数,也是自动供输弹系统的一项重要设计指标[1-2]。目前一般采用基于光学杠杆的姿态角测试方法测量弹丸卡膛姿态[3],即在弹丸引信安装处预装一个激光器,弹丸入膛后,激光器发射一束激光,投射到安装在身管口部的位置敏感器件(PSD)上,利用光学杠杆原理将弹丸姿态的微小变化量转换为PSD上光点的较大位移量,从而实现弹丸卡膛姿态的测量。此种方法需要改造弹丸,影响火炮的正常射击,仅适合在实验室内进行卡膛一致性测试。实际上,在研究火炮射击密集度,研究弹丸卡膛几何参数与密集度之间的关系时,需要测出当前弹丸的卡膛几何参数,同时记录下当前弹丸的弹着点坐标,根据一组或多组数据来分析卡膛几何参数与射击密集度之间的关系[4]。但是,由于目前还没有一种能够适用于射击现场的弹丸卡膛几何参数无损测试方法[5-6],使得射击现场试验数据缺乏,输弹系统的设计缺乏一定理论支撑,制约了火炮相关理论的发展。因此,亟待研究满足现场射击试验状态下的弹丸卡膛几何参数测试方法。基于此,本文提出一种适用于射击现场的基于位移传感器[7-8]阵列的卡膛几何参数测量方法,开展了卡膛几何参数测量装置设计,并采用该测量装置对弹丸卡膛状态下的几何参数进行实际测量,并通过实验验证了该测试系统测量的稳定性与准确性,为输弹系统设计提供理论依据。
1 弹丸卡膛几何参数测量原理
弹丸卡膛几何参数包括卡膛姿态和弹丸轴向位置。弹丸卡膛姿态测量装置组成如图1所示,包括弹丸尾端面参数测量模块、弹丸轴线测量模块、药室轴线测量模块、轴向位置测量模块及角度测量模块。其测量原理是:假设身管轴线与药室轴线同轴,卡膛前,事先通过弹丸尾端面参数测量模块采集弹丸轴线与弹丸尾端面上轮廓要素的几何关系。弹丸卡膛结束后,将弹丸卡膛姿态测量装置放置于膛内,由弹丸轴线测量模块测量本装置与弹丸尾部之间的夹角;由药室轴线测量模块测量本装置与药室轴线的夹角,即与身管轴线的夹角;由轴向位置测量模块测量进弹深度。最后将各模块的测量结果相互融合,通过数值计算,可以得到弹丸卡膛状态下的姿态角与轴向位置参数。
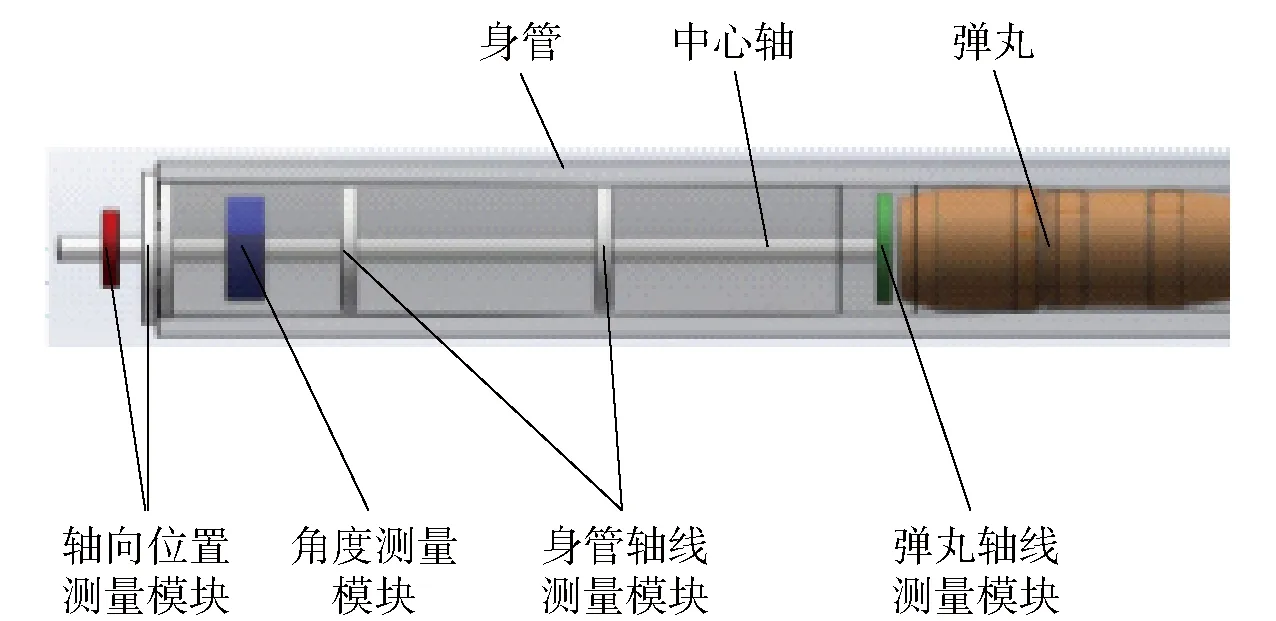
图1 卡膛状态测量装置组成与原理图Fig.1 Composition of measuring system
1.1 药室轴线测量模块
由两个平行的传感器阵列组成,每个传感器阵列分别由均匀分布在圆周上4个位移传感器组成,传感器的测量线沿身管径向方向,用来采集药室内膛轮廓信息,通过数据拟合获得药室轴线与膛内测试模块的几何关系。
1.2 弹丸轴线测量模块
由5个位移传感器组成,传感器阵列垂直于膛内测试模块轴线。其中4个传感器为位移传感器,传感器的测量线沿膛内测试模块轴线方向,用来采集弹丸尾端面的轮廓信息,通过数据拟合获得弹丸尾端面与膛内测试模块的几何关系;另一个传感器为标记识别传感器,标记识别传感器的作用是识别预先在弹丸底部设置的标记点,保证卡膛姿态测量装置采集到的弹丸尾端面信息与事先标定时一致。
1.3 弹丸轴向位置测量模块
弹丸轴向位置测试模块用来测量弹丸距离身管尾部的距离。
1.4 弹丸尾端面参数测量模块
弹丸尾端面测量模块用来测量弹丸尾端面的几何信息,用来修正弹丸尾端面的形位误差。
2 卡膛参数空间几何模型及其解算方法
2.1 弹丸卡膛参数空间坐标系建立
采用正交坐标系来描述弹丸卡膛参数的空间几何关系,3个坐标系之间的位置关系如图2所示。坐标系建立如下:
1)基准坐标系。身管坐标系OXYZ,O为药室轴线上任意一点;以药室轴线为Z轴,取炮尾指向炮口为正方向;以过O点的水平直线为X轴,取Z轴正方向向右为正;再利用右手法则确定出Y轴。
2)卡膛姿态测量装置坐标系OjXjYjZj,Oj为卡膛姿态测量装置中心轴线上任意一点;以卡膛姿态测量装置中心轴线为Zj轴,取炮尾指向炮口为正方向;再利用右手法则确定出Xj轴、Yj轴,保证各位移传感器在OjXjYjZj平面上的投影均位于坐标轴上。
3)弹丸坐标系OpXpYpZp,Op为弹丸轴线上任意一点;以弹丸轴线为Zp轴,取弹尾指向弹头方向为正方向;再利用右手法则确定出Xp轴、Yp轴。
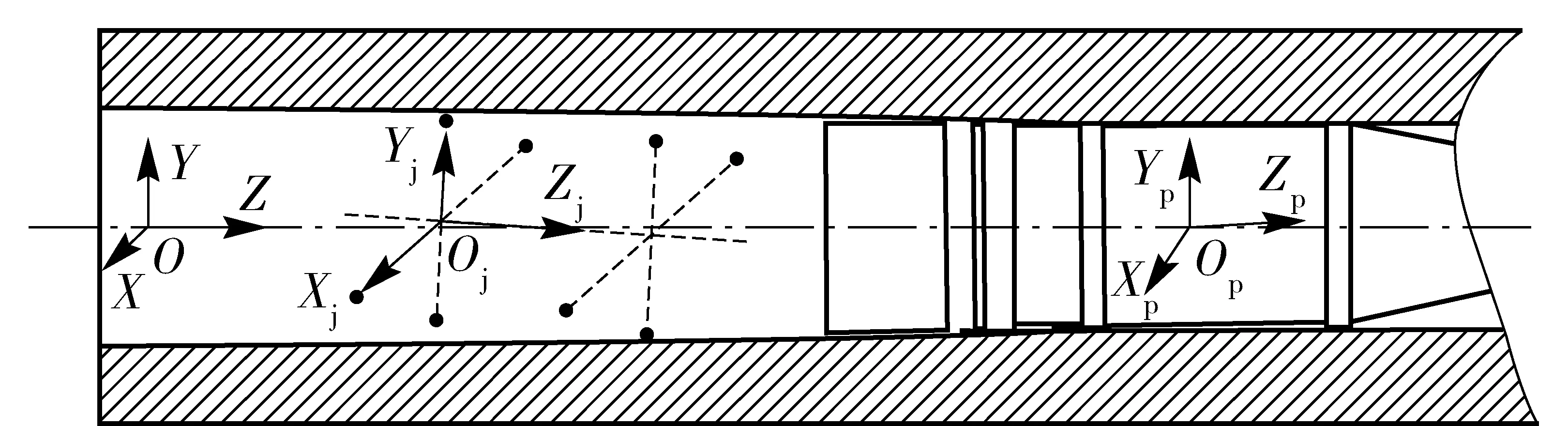
图2 坐标系位置关系示意图Fig.2 Location relation of coordinate system
2.2 药室轴线测量模型
药室轴线测量模型如图3所示,根据药室轴线测量模块的8个位移传感器输出,可得到药室内圆锥面上8点A、B、C、D、E、F、G、H在卡膛姿态测量装置坐标系OjXjYjZj中的坐标,分别如下:A(LA,0,0),B(0,LB,0),C(-LC,0,0),D(0,-LD,0),E(LE,0,l),F(0,LF,l),G(-LG,0,l),H(0,-LH,l),其中,LA~LH为传感器输出,l为两个传感器阵列的轴向距离。
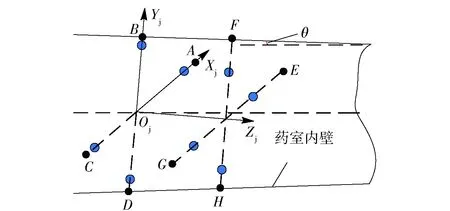
图3 药室轴线测量模型Fig.3 Measurement model of chamber axis
设药室的轴线为(m,n,1),锥面顶点的坐标为(x0,y0,z0),圆锥角的一半为θ,则空间圆锥面的方程可以表示为
[m(x-x0)+n(y-y0)+(z-z0)]2=
λ[(x-x0)2+(y-y0)2+(z-z0)2](m2+n2+l),
(1)
式中:λ=(cosθ)2.
将圆锥面上的A~H的坐标代入(1)式中,建立一个非线性超定方程组,即可解算出药室轴线坐标(m,n,1)、圆锥顶点(x0,y0,z0)及1/2圆锥角θ.
2.3 弹丸轴线测量
弹丸轴线测量模型如图4所示,根据轴向测量模块的4个位移传感器的输出,可以给出弹丸端面的4个点I、J、K、L在膛内测试模块坐标系OjXjYjZj中的坐标,分别如下:I(r,0,LI)、J(0,r,LJ)、K(-r,0,LK)、L(0,-r,LL),其中r为传感器阵列圆周的半径。
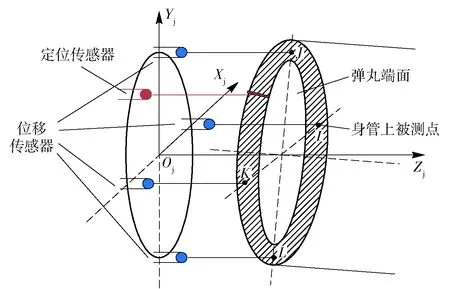
图4 弹丸轴线测量模型Fig.4 Measurement model of projectile axis
设弹丸尾端面的法向量为(a,b,c),则平面的方程可以表示为
ax+by+cz+1=0.
(2)
将I~L点的坐标代入(2)式,建立一个非线性超定方程组,即可解出法向量在坐标系OjXjYjZj中的坐标为(a,b,c)。
2.4 弹丸尾端面信息测量模型
若弹丸为理想的回转体,那么弹丸尾端面的法向量即可等效为弹丸的轴线向量。但在实际情况下,该测试模型中的弹丸尾端面的法向量与弹丸轴线存在着较大差异,因此需要对弹丸尾端面的几何信息进行测量,并代入上述模型进行修正。
弹丸尾端面信息测量模块原理如图5所示,根据弹丸尾端面参数测量模块的位移传感器的4个输出,可以给出弹丸端面的4个点I、J、K、L在弹丸坐标系OpXpYpZp中的坐标,分别如下:I′(r,0,LI),J′(0,r,LJ),K′(-r,0,LK),L′(0,-r,LL)。
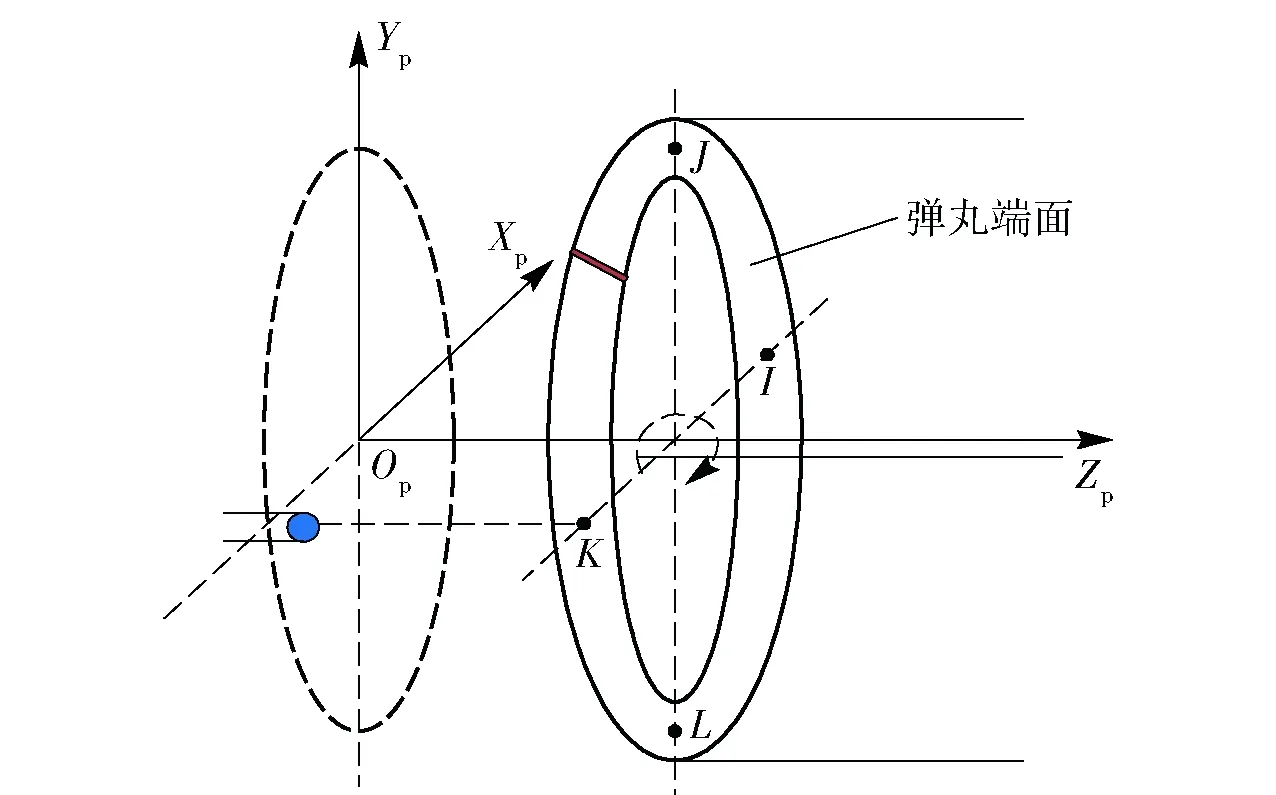
图5 弹丸尾端面信息测量模型Fig.5 Measurement model of end surface of projectile
在该坐标系中,弹丸轴线的向量坐标为(0,0,1),设弹丸尾端面的拟合平面的法向量为(a1,b1,c1),则平面的方程可以表示为
a1x+b1y+c1z+1=0.
(3)
将I′~L′点的坐标代入(3)式,建立一个非线性超定方程组,即可解出法向量在坐标系OpXpYpZp中的坐标为(a1,b1,c1)。
2.5 弹丸卡膛几何参数解算方法
为了得到最终弹丸轴线在身管坐标系OXYZ中的坐标,需要对3个坐标系中的坐标进行转换统一。首先,弹丸轴线在弹丸坐标系OpXpYpZp中的坐标为dp(0,0,1),利用弹丸坐标系OpXpYpZp与将其转换到膛内测试系统坐标系OjXjYjZj的关系建立坐标旋转矩阵Qj,得到其坐标为
dj=Qjdp.
(4)
同样,利用膛内测试系统坐标系OjXjYjZj与身管坐标系OXYZ的关系,建立旋转矩阵Q然后,在将该坐标转到身管坐标系中,得到其在身管坐标系中的坐标为
dp=Qdj.
(5)
在身管坐标系中,药室轴线的坐标为s(0,0,1),那么弹丸的卡膛角为
φj=arccos(sdp),
(6)
偏航角和俯仰角分别为
(7)
式中:xdp、ydp、zdp分别为dp在X、Y、Z轴的坐标。
2.6 弹丸轴向位置解算方法
如图6所示,l1为弹丸轴向测量模块的测试结果,由游标卡尺测试两个平面之间的距离,l2为装置的长度(结构设计尺寸,再通过校准确定),l3由弹丸轴向测量模块的输出计算获得。
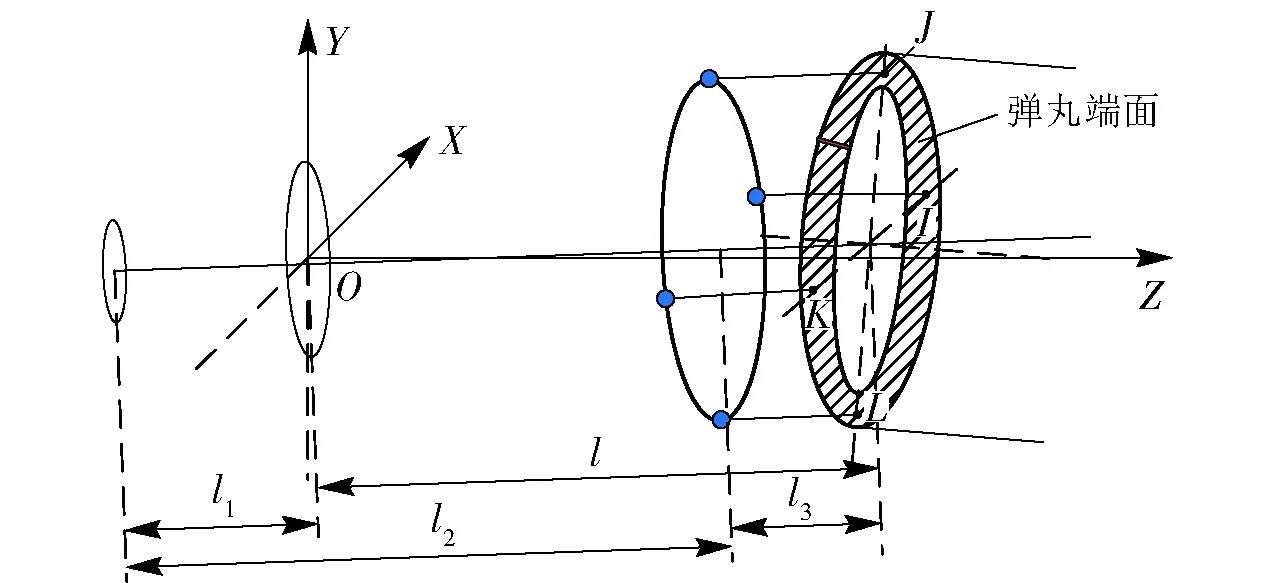
图6 弹丸轴向位置几何模型Fig.6 Geometric model of axial position of projectile
由图6可知,药室轴线在膛内测试坐标系的归一化坐标为nj,测试模块中心轴线的坐标为(0,0,1),两轴线夹角的余弦值为znj.
图6中所涉及的长度均为膛内测试中心轴线方向的距离,因此需要投影到药室轴线方向,则弹丸的轴向力身管尾部的距离为
l=(l2-l1+l3)znj,
(8)
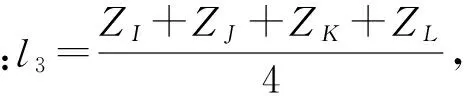
3 弹丸卡膛几何参数测量装置性能测试
在现有条件下,难以对整个测量装置进行标定,现分别对各测试模块单独进行测试分析。膛内测试模块实物照片如图7所示。
3.1 药室轴线测量分析
药室轴线测量模块通过采集药室表面的轮廓信息,将药室当作一个圆锥面进行重构。药室轴线测量模块调试实验是将膛内测试模块放入药室段,然后旋转中心轴,同步采集8个位移传感器的输出,将输出信号带入药室轴线解算模型,重构药室内轮廓面。根据身管设计尺寸,药室1/2圆锥角为0.33°,实测身管内膛圆锥角变化如图8所示,测得的圆锥角最大值0.333°,最小值为0.331°,峰- 峰值为0.002°,均值为0.332°,最大相对误差为0.30%.
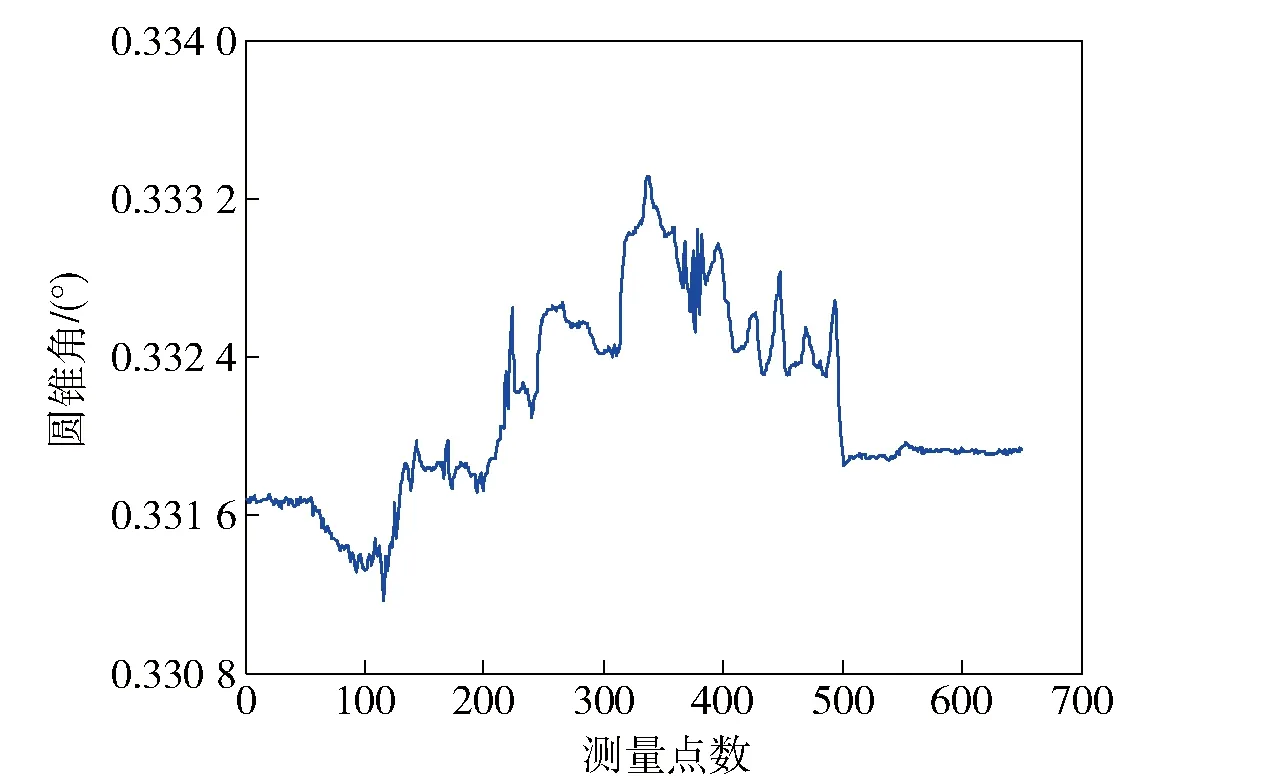
图8 1/2圆锥角的变化曲线Fig.8 Curve of 1/2 cone angle
根据药室轴线的坐标,计算药室轴线与测试系统中心轴线的夹角如图9所示。从图9中可以看出,该夹角在测量装置转动的过程中,夹角也在一定程度地变化,变化的范围为4.73′~6.21′.
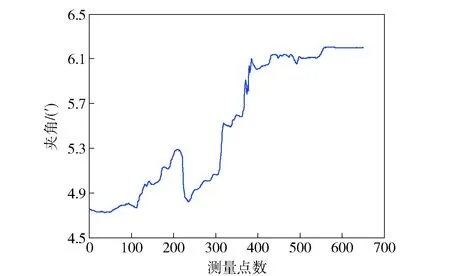
图9 中心轴线与药室轴线夹角变化曲线Fig.9 Curve of angle between central axis and chamber axis
经过对比实验中多组数据,本测试系统多次动态测量得到的内膛圆锥角与设计理论值非常接近,装置中心轴线与药室轴线夹角较小,测试结果稳定,测量可靠性高。
3.2 弹丸轴线测量分析
如图10所示,将卡膛几何参数测量装置用V型座支撑,调节支撑座螺杆,使得测量装置的轴线基本水平;调节弹丸支撑螺杆,使弹丸基本水平,使轴向电涡流位移传感器的输出均在合适的区域内;调节到位后,利用微调弹丸旋转支撑装置的调节弹头高度,模拟弹丸角度变化。
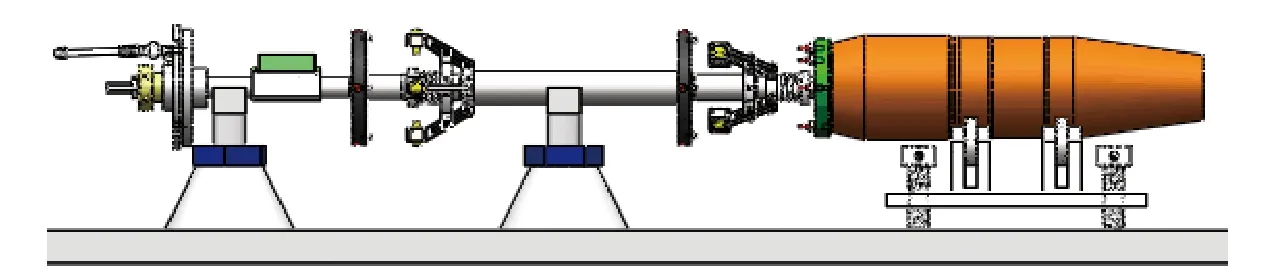
图10 轴线测量模块实验装置图Fig.10 Experimental device for measuring module of axis
根据弹丸旋转支撑装置的设计尺寸,两组调节螺栓在弹丸轴线方向的距离为300 mm,由于弹丸在初始位置为水平状态,那么调节螺杆上升距离Δh后,弹丸轴线与初始位置的夹角为
Δθ=arcsin(|Δh|/300).
(9)
将上升距离Δh代入(9)式,算出弹丸轴线与初始位置夹角理论值见表1第6列。
然后,将轴线测量模块对应各点的输出转化为K、J、I、L4个点在测量坐标系OjXjYjZj中的坐标,解算弹丸轴线在坐标系OjXjYjZj中的坐标、弹丸轴线与初始位置夹角的测量值的设定值与测量值,见表1.
从表1中可以看出,当螺杆上升的距离Δh较大时,弹丸轴线与初始位置夹角的测量值与理论值的相对误差范围为6%~12%,弹丸轴线测量的输出结果误差较大,这是因为弹丸本身并不是一个理想的回转体,尾端面加工精度较低,测试装置中心轴线与弹丸轴线变化的平面不一致,所以弹丸尾端面的法向量不能简单等效为弹丸的轴线向量,该测试模型中的弹丸尾端面的法向量与弹丸轴线存在较大的差异,因此有必要对实际弹丸尾端面的几何信息进行测量,并带入上述模型进行修正。
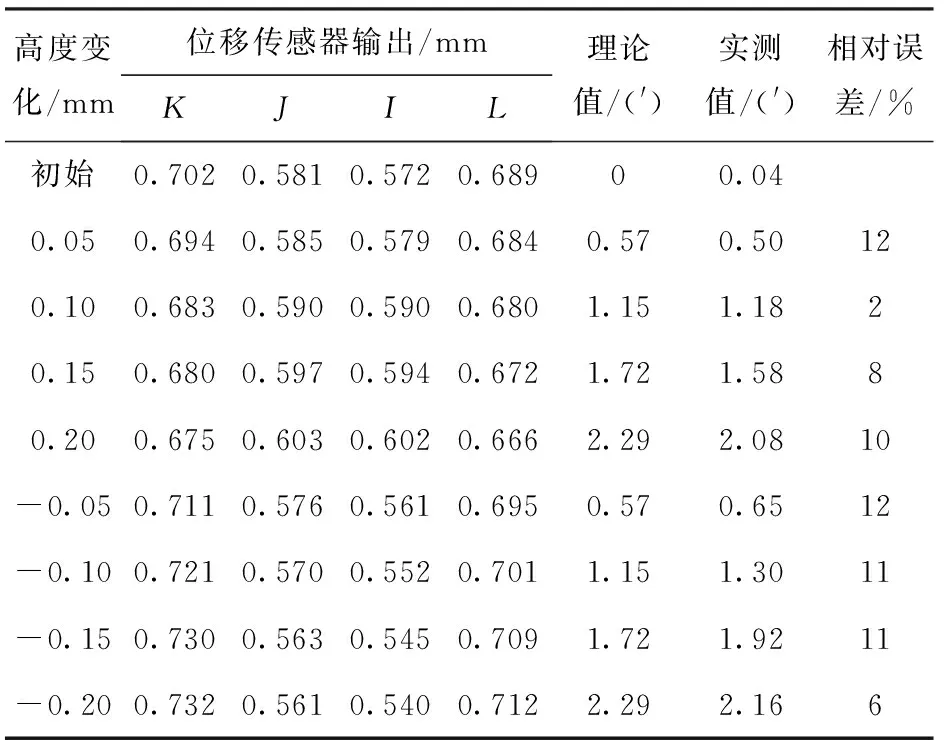
表1 弹丸轴线测量模块测量结果
3.3 弹丸尾端面信息测量分析
弹丸尾端面信息测量实验方法为:将弹丸尾端面涂上标记,然后旋转弹丸,并记录电涡流位移传感器对准弹丸尾端面上标记点时的响应,测试结果见表2. 从表2可以看出,采用该方法测量弹丸尾端面信息,相同位置处位移传感器的输出的标准差最大为0.032 V(0.004 mm),弹丸尾端面法线与弹丸轴线的夹角8组测量值输出平均值为2.61′,最大相对误差为1.149%,根据贝塞尔公式求出的单次测量标准差最大为0.035′.
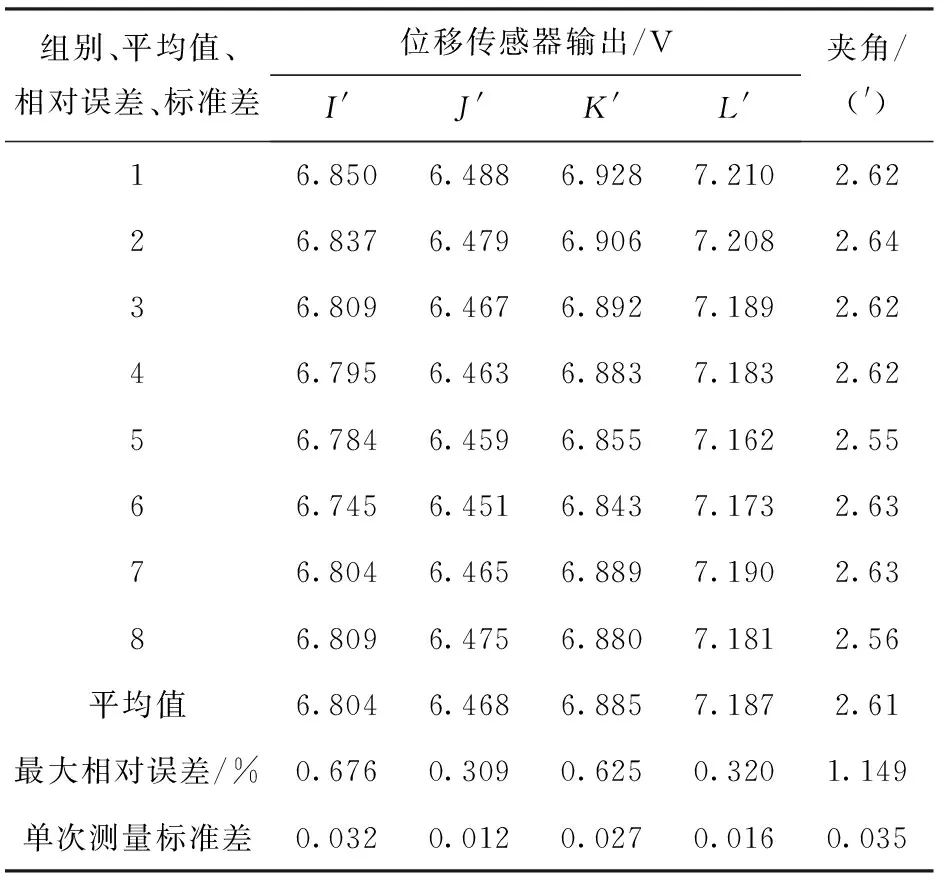
表2 弹丸尾端面信息测试模块实验数据
3.4 测试系统实验分析
在主射向、1 083 mil的射角下,将弹丸输入膛内,完成卡膛过程。然后,将卡膛参数测量装置放入身管内膛进行测量,对本次卡膛状态进行3次测试,将弹丸尾端面信息带入弹丸轴线测量模型,对实际模型中的弹丸轴线进行修正,最终测量结果见表3.
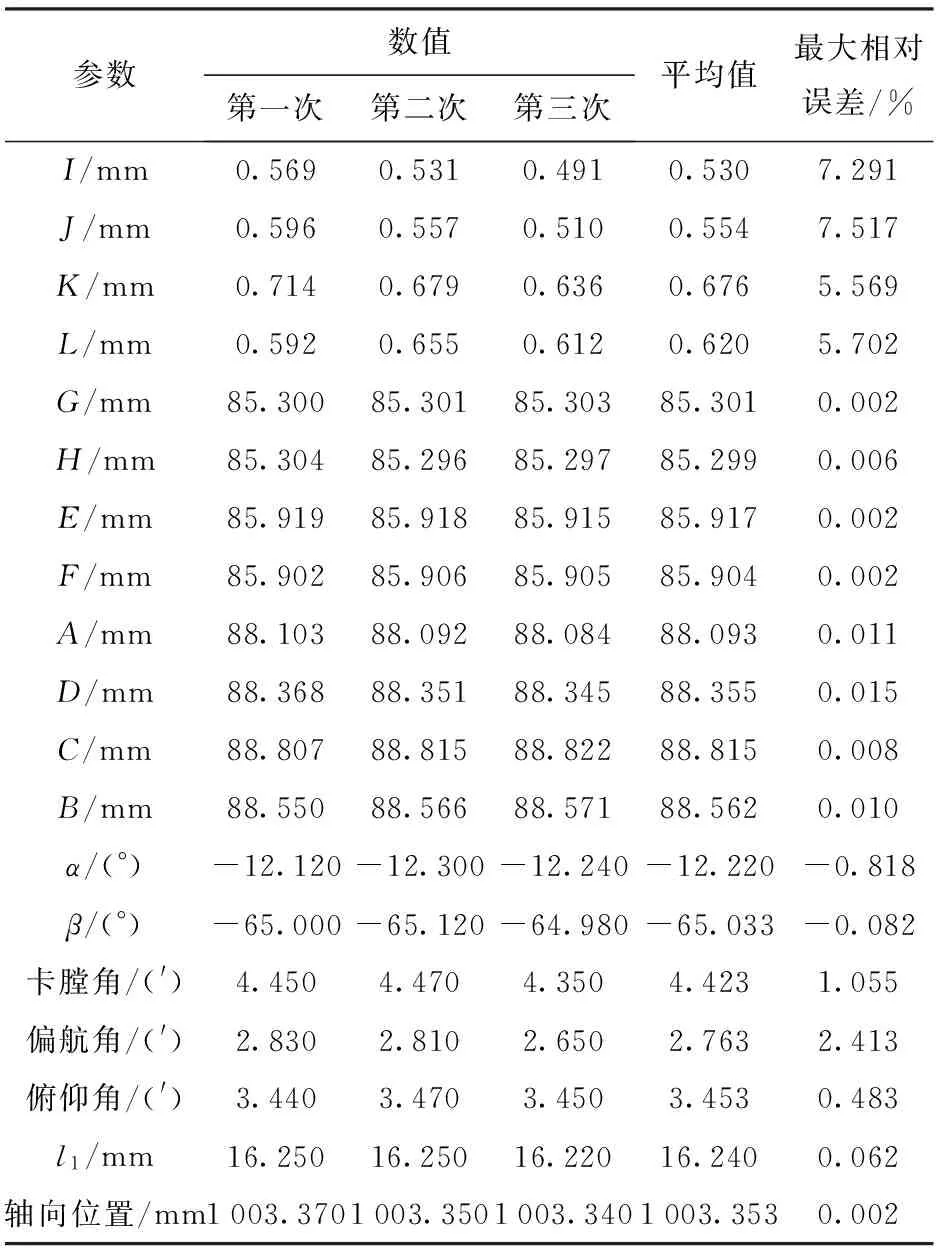
表3 1 083 mil射角下的实验数据
每组测试的3次测量结果见表3,其中卡膛角、偏航角、俯仰角、弹丸轴向位置的多次测量均值分别为4.423′、2.763′、3.453′,其最大相对误差分别为1.055%、2.413%、0.483%. 对上述3次卡膛状态的测试结果分析可知,本测试方法能稳定的工作,各参数取得了较好的测试结果,满足了射击现场无损测量卡膛几何参数的试验要求。
4 结论
本文针对大口径火炮弹丸卡膛几何参数现场测量要求,提出一种适用于射击现场的弹丸卡膛
姿态的无损测试方法,建立了弹丸卡膛参数的空间几何模型,分别介绍了药室轴线、弹丸轴线以及测量装置轴线的测量及解算方法,对测试系统的各个模块进行了验证实验,系统的测量姿态角范围为0°~2°,测量精度为0.001′. 在此基础上,对射击现场弹丸卡膛状态下的几何参数进行测量实验,通过分析实验结果验证了该测试系统的稳定性与准确性。
References)
[1] 李伟, 马吉胜, 孙河洋,等. 弹丸惯性卡膛冲击问题动力学研究[J]. 振动与冲击, 2011, 30(5):161-163. LI Wei, MA Ji-sheng,SUN He-yang,et al. Dynamic analysis for inertial bayonet-chamber process of a projectile[J]. Journal of Vibration and Shock, 2011, 30(5):161-163. (in Chinese)
[2] 赵良伟, 王惠源, 张鹏军,等. 火炮惯性输弹初始参数对弹丸卡膛稳定性的影响[J]. 中北大学学报, 2014, 35(2):111-116. ZHAO Liang-wei, WANG Hui-yuan, ZHANG Peng-jun,et al. The influence on projectile bayonet-chamber stability by initial parameter in artillery[J]. Journal of North University of China, 2014, 35(2):111-116. (in Chinese)
[3] 陆文广, 芮筱亭, 顾金良,等. 弹丸膛内姿态与纵向运动测试与分析[J]. 兵工学报, 2006, 27(1):149-153. LU Wen-guang, RUI Xiao-ting, GU Jin-liang,et al. Test and analysis of attitude and movement of projectile in bore[J]. Acta Armamentarii, 2006, 27(1):149-153. (in Chinese)
[4] 张睿, 陈卫国, 刘闯. 弹丸卡膛姿态测试系统设计与实现[J]. 兵器装备工程学报, 2016, 37(1):27-30. ZHANG Rui,CHEN Wei-guo,LIU Chuang. Design and implementation of projectile attitude testing system[J].Journal of Ordnance Equipment Engineering, 2016, 37(1):27-30.(in Chinese)
[5] 龚长红, 杨云飞, 黄林昊. 现代火炮炮膛烧蚀磨损机理及控制措施[J]. 四川兵工学报, 2014, 35(11):127-129. GONG Chang-hong,YANG Yun-fei,HUANG Lin-hao. Modern artillery bore erosion wear mechanism and control measures[J]. Journal of Sichuan Ordnance, 2014, 35(11):127-129. (in Chinese)
[6] 张喜发. 火炮烧蚀内弹道学[M]. 北京:国防工业出版社, 2001:15-18. ZHANG Xi-fa. Ablation of artillery interior ballistics[M].Beijing: National Defense Industry Press, 2001:15-18. (in Chinese)
[7] Vyroubal D, Zele D. Experimental optimization of the probe for eddy-current displacement transducer[J]. IEEE Transactions on Instrumentation and Measurement, 1993, 42(6):995-1000.
[8] Vyroubal D. Eddy-current displacement transducer with extended linear range and automatic tuning[J]. IEEE Transactions on Instrumentation and Measurement, 2009, 58(9):3221-3231.
The Measuring Method for Geometric Parameter of Bore Jamming Based on Displacement Sensor Array
PENG Peng, DI Chang-an, WANG Zhe-jun
(School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, China)
The loading precision of projectiles and the consistency of bore jamming of large caliber barrel have a great impact on the bore wear and firing accuracy. Based on the bore jamming status of large caliber projectile, a nondestructive measuring method is presented for measuring the geometric parameters of projectile muzzle in firing field. The measurement principle and system composition of the measuring method are introduced. The measurement models of the axis of chamber, the axis of projectile and the tail end of projectile are established, and the performance of each measurement module is analyzed and verified. On this basis, the geometric parameters of projectile are measured by the proposed measuring system. The stability and accuracy of the measuring system are verified through the analysis of the experimental results.
ordnance science and technology; bore jamming; attitude test; coordinate transformation; displacement measurement; obliquity
2016-06-02
彭澎(1991—), 男, 博士研究生。E-mail: pp802799@163.com
狄长安(1973—), 男, 教授,博士生导师。E-mail:dichangan@njust.edu.cn
TJ306+.1
A
1000-1093(2017)02-0240-06
10.3969/j.issn.1000-1093.2017.02.005

