“根系课堂”三种课型

文 | 高金德

“根系课堂”三种课型

文 | 高金德

问题生发型课堂—— 一图孕育万题

问题生发型课堂是指以教师设计的典型问题为学生思考的切入点，借助学生已有的认知能力以提出问题、优化问题并形成系统性问题的方式来呈现自我思维活动的课堂过程。在这样的课堂中，学生将经历一个尝试提出问题、辩论提出问题的合理性、优化并形成系列问题的过程。如此一来，学生思考的切入点正如一粒思维的种子，在学生思维活动的过程中开始了“生长发育”，于是，一个问题系统建构起来了。

课堂案例：

1、典型问题：

如图1，在平面直角坐标系中，二次函数y=-x2+2x+3的图象与x轴交于A、B两点，与y轴交于点C，点P是直线BC上方抛物线上的一个动点，请同学们根据条件以及函数图象所包含的信息，结合自己的学习经验，提出问题。

2、问题生发思维图：

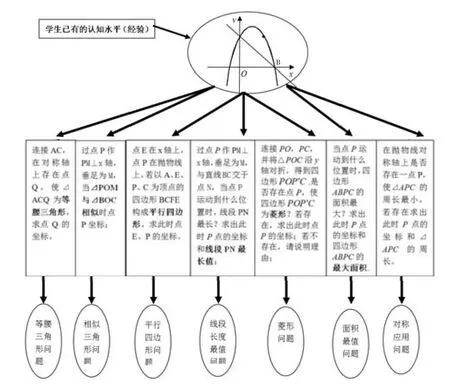
图1

专题突破型课堂案例—— 多题策略归一

专题突破型课堂是指以师生共同设计的同类专题为学生思考的切入点，借助学生已有解决问题的经验，以方法的生成与验证来呈现自我思维活动的课堂过程。在这样的课堂中，学生一般将经历一个独立思考、深度合作的方法生成与验证的过程，并将方法生成的过程形成以思维导图为形式的解题策略。一般来讲，小专题需要一课时，大专题一般要多课时。

课堂案例：（本专题案例的探究用了一周的时间）

一、典型问题

1、2014年12月1日用题（周一）

如图2，抛物线y=ax2+bx+c（a≠0）经过点A（-3，0）、B（1，0）、C（-2，1），交y轴于点M。

（1）求抛物线的表达式；

（2）抛物线上是否存在一点P，作PN垂直x轴于点N，使得以点P、A、N为顶点的三角形与△MAO相似？若存在，求点P的坐标；若不存在，请说明理由。

2、2014年12月2日用题（周二）

如图3，已知抛物线y=x2+2x经过B（-3，3），C为顶点。

3、2014年12月3日用题（周三）

如图3，已知抛物线y=x2+2x经过B（-3，3），C为顶点。P是抛物线上的第二象限内的动点，过点P作垂直线，垂足为M，是否存在点P，使得以P、M、O为顶点的三角形与△BOC相似？

4、2014年12月4日用题（周四）

如图4，直线y=2x+2与x轴交于点A，与y轴交于点B，把△AOB沿y轴翻折，点A落到点C，过点B的抛物线y=-x2+bx+c与直线BC交于点D（3，-4）。

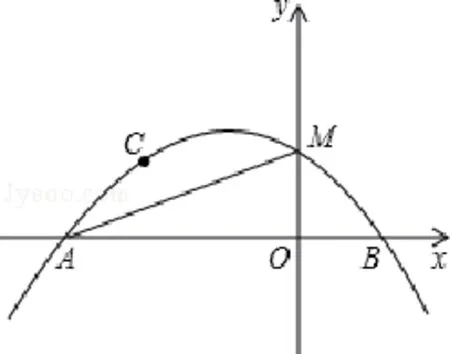
图2

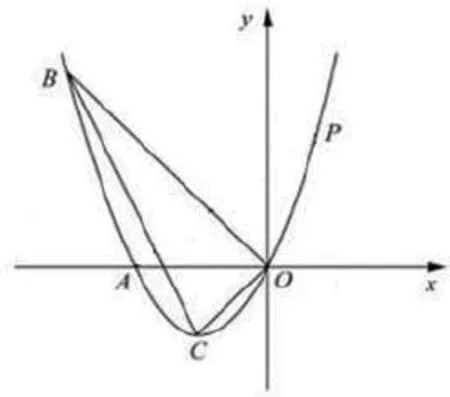
图3

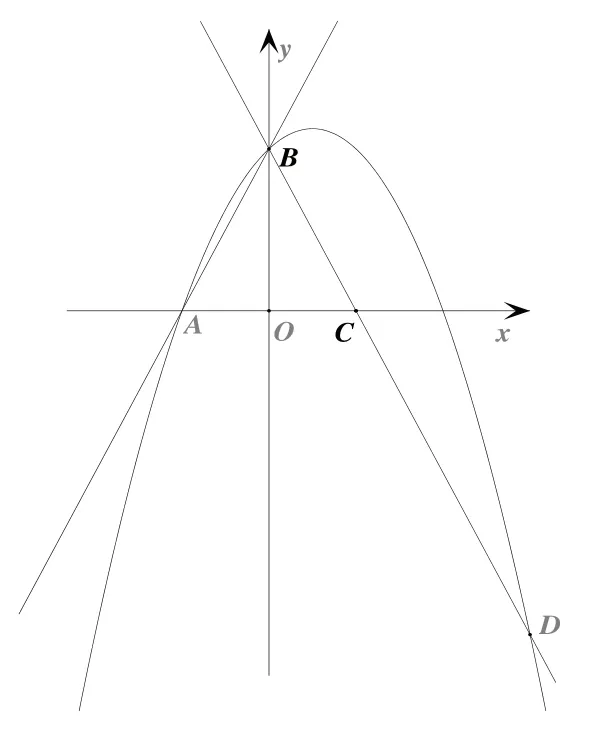
图4

（1）求直线BD和抛物线的解析式；

（2）在第一象限内的抛物线上，是否存在一点M，作MN垂直于x轴，垂足为点N，使得以M、O、N为顶点的三角形与△BOC相似？若存在，求出点M的坐标；若不存在，请说明理由；

二、策略生成思维图

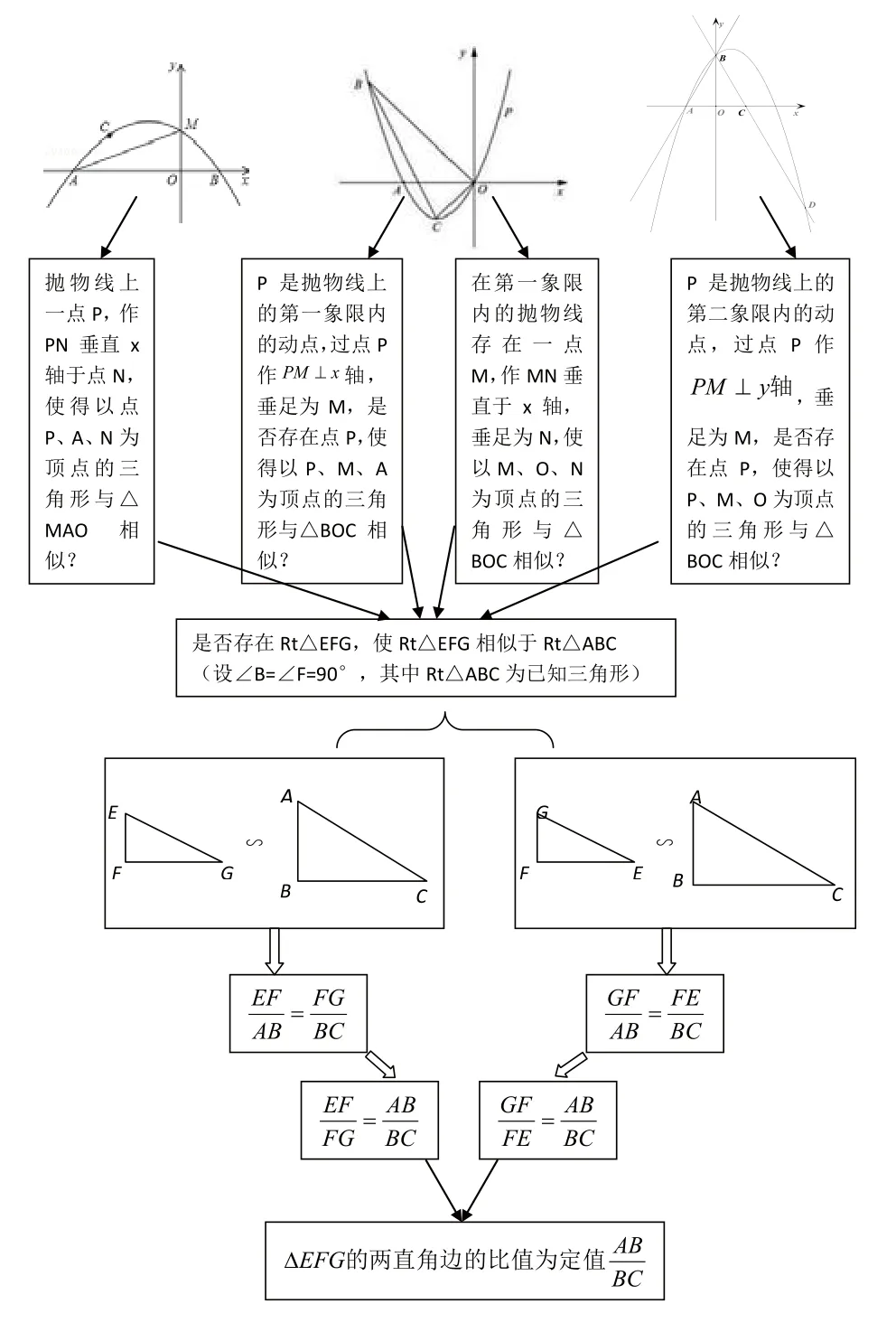
图5

新题研发型课堂—— 旧题研发新题

要让我们的孩子现在就成为研究型的学者，而不是为将来培养出研究的学者，只有今天孩子已经拥有研究型的习惯，将来才有可能成为某个领域爱好研究的人。

新题研发型课堂是指以师生共同研究过的专题为再思考的切入点，借助学生联想能力生发生成新的问题、新的方法、新的策略。这些新问题一般要超越已经练习过的问题，其使用的方法一般要在原有经验基础上进行突破。在这样的课堂中，学生的思维过程既需要借助已有思维的经验，更要勇于突破思维的定势，形成一种全新的思维方式解决新问题。这是一种挑战不可能的课堂，这是一种超越学习课堂的研究型课堂，这是一种寻觅新知识、新问题、新方法的课堂。这样的课堂不局限于一节课、两节课，要给学生充足的时间，要给学生深度合作交流的机会，要凝聚集体的力量来创新。

课堂核心流程：

一、教师准备的问题：

1、通过下面曾经解决过的数学问题，说出你的解题策略和重要环节。

如图6，在平面直角坐标系中，二次函数Y=-X2+2X+3的图象与x轴交于A、B两点，与y轴交于点C，点P是直线BC上方抛物线上的一个动点。过点P作PM⊥x轴，垂足为M，与直线BC交于点N，当点P运动到什么位置时，线段PN最长？求出此时P点的坐标和线段PN最长值。

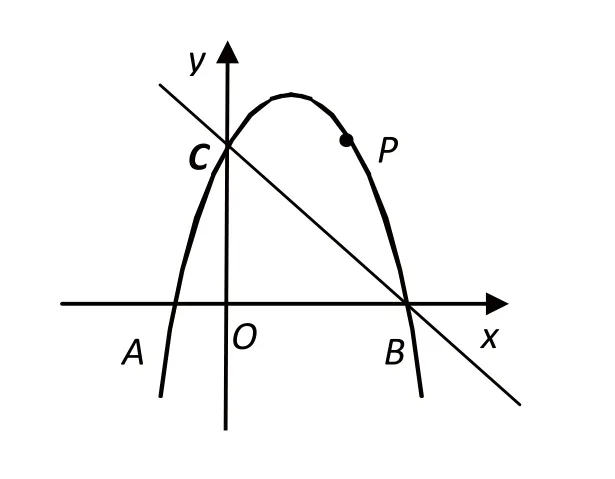
图6

2.凭借上题的经验，能否在更广阔的数学领域内研发新题，即我们教材中、参考书中、中考题中从未发现的数学问题。（挑战不可能）

二、学生的新发现：

新的数学问题（本问题目前来讲，在教材、参考书、中考题中很难查到）

图7

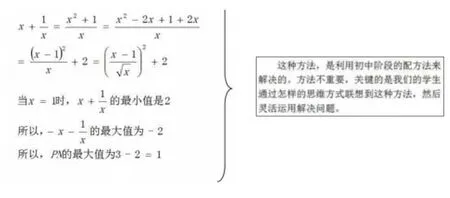
借助已有的经验得出的核心关系式：

再一次形成新的数学问题：

新的解题方法：

方法一：

从而得出PN的最大值为1.

方法二：