内胆式双热型生物质热解反应器内传热过程建模分析
李三平, 孙 雪, 王述洋
(东北林业大学 机电工程学院, 黑龙江 哈尔滨 150040)
内胆式双热型生物质热解反应器内传热过程建模分析

LI Sanping
李三平, 孙 雪*, 王述洋
(东北林业大学 机电工程学院, 黑龙江 哈尔滨 150040)
在对自行设计的内胆式双热型生物质热解反应器内热量传递过程分析的基础上,针对反应器内部传热复杂的特点,既有生物质颗粒与热床料之间的热传导,也有生物质颗粒与热载气之间的对流换热,还包括热壁面对生物质颗粒及床料的辐射换热等多种传热方式,建立了反应器的壁面传热、颗粒间传热和二维对流换热的数学模型;并通过仿真分析对传热模型进行了验证,得出该耦合仿真模型基本满足生物质颗粒快速热裂解条件,并预测出口气相平均温度均为720 K。
生物质热解;传热过程;传热模型;仿真
在对流化工艺及流化床研究的过程中,研究者为了便于对流化床反应器进行设计和理论分析,一般先对反应器进行数学建模,然后进行仿真模拟,最后再进行工程放大及优化,这样可以极大地减少开发成本,并缩短开发周期[1]。在流化床反应器内同时存在热传导、对流换热和辐射换热3种传热方式,涉及到固体颗粒之间、固体颗粒与气体以及换热表面之间等传热过程,十分复杂。因此,国内外很多研究者一般先分析床内热量传递规律,然后建立其物理模型,再通过实验来获得其特征数方程,从而预测出床内的传热系数[2]。然而,描述床内传热问题的精确数学模型仍需要进一步研究。本研究旨在结合现有流化床传热模型,针对自行设计反应器的流化工艺[3],分析反应器内热量传递过程,分别建立反应器的壁面传热、颗粒间传热以及二维对流换热模型,并通过仿真分析进行验证,为对反应器内传质传热过程进行仿真研究提供基础数据。
1 反应器内热量平衡
反应器流化工艺为:在反应器内胆和外筒之间通入热烟气,在内胆中通入流化气体(不凝气体)对床料进行流态化处理,热烟气通过和内胆壁进行对流换热和辐射换热将热量传递到壁面,并通过对流换热、碰撞导热及辐射换热加热载气和床料颗粒;当加热到给定温度时再由螺旋进料器加入生物质粉末,通过其与热载气、热床料及壁面之间的热量传递来加热生物质颗粒,实现生物质颗粒的热裂解[1]。反应器内部传热过程包括生物质颗粒与热床料间的热传导,生物质颗粒与热载气之间的对流换热,以及壁面对生物质颗粒及床料的辐射换热,涉及的热量关系如图1所示。

图1 反应器内所涉及的热量关系示意图Fig.1 The diagram of heat relation involved in the reactor
反应器内部获得的热量主要由外筒和内胆之间的热烟气提供,消耗的热量主要包括加热不凝气体、生物质颗粒、热载体(石英砂)颗粒和壁面等所耗费的热量以及外筒壁和环境中空气自然对流换热引起的热量损失等。其中热烟气所释放的热量主要通过对流换热和辐射换热2种方式传递给壁面。由反应器内部热平衡可得:
Qf=Qsr+Qsv=Qb+Qn+Qq+Qw+Q1
(1)
式中:Qf—热烟气所释放的热量,kJ;Qsr,Qsv—分别为热烟气与壁面间的辐射换热量、对流换热量,kJ;Qb—生物质颗粒吸收的热量,kJ;Qn—不凝气体吸收的热量,kJ;Qq—热载体颗粒吸收的热量,kJ;Qw—壁面吸收的热量,kJ;Q1—系统损失的热量,kJ。
由式(1)可知,为了实现反应器内部热平衡,确定生物质颗粒完全热裂解所需热量,必须对该反应器的壁面传热、颗粒间传热以及二维对流换热模型进行研究。
2 反应器内传热模型的建立
2.1 研究现状
目前,关于建立流化床内传热问题的数学模型的研究还处在发展阶段,现有研究主要针对特定反应器内传热方式来建立其传热数学模型。典型的流化床传热模型有气膜控制模型[4]、颗粒传热模型[5]、乳化团传热模型[6]、通用传热模型[7]和经验模型[8]等,但由于不能全面理解床内的传热机理,各模型均不能够准确地描述床内传热问题。国内,黄文迪等[9]对气固流化床内的传热规律进行了研究,建立了床内颗粒间的辐射换热模型,并通过分析得出颗粒尺寸对颗粒间辐射换热系数和气膜导热系数有不同的影响;郭雪岩等[10]采用欧拉-欧拉模型对Geldart提出的D类颗粒气固流化床的非定常传热过程进行了模拟;李锦时等[11]应用中子输运模型、耦合气固传热模型以及气固双流体模型,对流化床核反应器内气固流动和热动力特性进行了数值模拟。上述数学模型都有一定的针对性和使用局限性,建立通用的传热数学模型仍有待于进一步研究。
2.2 壁面传热模型的建立
内胆式双热型反应器内的床层由颗粒相和气体分散相组成,其中颗粒相主要是由很多松散连在一起的生物质颗粒与床料粒子和小气泡构成的颗粒絮团组成。在热量传递的过程中,靠近壁面处的颗粒絮团的温度高于床层内部的颗粒絮团,故而其物性不同,使壁面处的局部空隙率高于床层内的空隙率,增大了壁面与颗粒相之间的传热热阻,因此,可以假设在接近壁面处存在一个气膜热阻。典型的流化床传热模型中,乳化团传热模型和通用传热模型均考虑了颗粒相物性参数的变化以及气泡等对传热过程的影响,且较符合流化床内部传热规律[6-7],笔者综合2种传热模型的特点,提出内胆式双热型反应器内壁面传热的物理模型如图2所示。模型假设颗粒絮团与壁面接触时,在接近壁面的区域内存在一个厚度为δW的气膜热阻(RW)。

图2 床层与壁面间传热的物理模型Fig.2 The heat transfer model between bed and wall
为准确描述反应器的热传导,同时考虑方便推导,模型假设条件:1)颗粒絮团各向同性,且在床层内部分布均匀;2)颗粒絮团在生存期(tw)内与气膜接触,并进行非稳态导热,生存期结束后,絮团破裂进入分散相;3)颗粒絮团与气膜间的非稳态导热热阻串联构成床层与壁面间的热阻,忽略分散相与壁面间的对流换热及辐射换热的影响;4)气膜热阻(RW)不受时间变化的影响,且气膜内无热量累积。
根据假设将壁面与床层间的物理模型简化成图2(b)所示的模型,其热传导的数学模型为:
(2)
式中:T(x,t)—温度,K;t—时间,s;a—导温系数,m2/s,满足a=λs/(ρsCs),λs(W·(m-1·K-1)为颗粒絮团的热导率,ρS(kg·m-3)为颗粒絮团的密度,Cs(J·kg-1·K-1)为颗粒絮团的比热;TB—初始时刻颗粒絮团的温度,K;qi—通过气膜的热流密度,W/m2。
根据假设热量在气膜内没有累积,故在管壁附近区域的热流密度应与通过气膜的热流密度以及传给床层的热流密度相等,即:
(3)
式中:RW—气膜热阻,满足RW=δW/λg,(m2·K)/W;δW—气膜厚度,m;λg—气膜的热导率,W/(m·K);hi—床层与壁面间的瞬时传热系数,W/(m2·K);TW—壁面的温度,K。
利用拉普拉斯变换,联立式(2)和(3)可求得:
(4)

考虑到颗粒絮团在壁面处的停留时间可用tW到tW+dt内颗粒絮团占据壁面的分布率函数I(t)描述,于是可求得平均传热系数:
(5)
2.3 颗粒间传热模型的建立
一般认为气固流化床中有3种形式的传热存在于颗粒与颗粒之间:1)颗粒间的辐射换热;2)颗粒间在接触处的导热;3)颗粒间缝隙内气膜的非稳态导热。笔者将后2种方式合并在一起讨论,建立颗粒间辐射换热模型和颗粒间导热模型。
2.3.1 颗粒间辐射换热模型
2.3.1.1 角系数 流化床内两颗粒之间的距离与颗粒粒径满足:
(6)
式中:s—两颗粒间的距离,m;εmf—临界流化状态下床层的空隙率;εf—实际操作状态下床层的空隙率;dp—颗粒的直径,m。
另根据角系数的定义,可推得两颗粒间的辐射角系数为[9]:
(7)
式中:y1=1+sin2β1+(sinβ1-sinβ2)2-2sin2β1cos(θ1-θ2);y2=1+sin2β2+(sinβ1-sinβ2)2-2sin2β2cos(θ1-θ2);r=(2s/dp-cosβ1-cosβ2)2+(sinβ1-sinβ2)2-2sinβ1sinβ2cos(θ1-θ2)+sin2β1+sin2β2;β1,β2—两表面之间的连线与各自表面的法线之间的夹角;θ1,θ2—两表面的极角。
将式(6)代入式(7)即可求得相邻两颗粒间的辐射换热角系数。
2.3.1.2 辐射换热系数 为了便于描述床内颗粒之间的辐射换热量,简化假设:1)床内颗粒群由两种温度不同的冷热理想球形颗粒组成,两种颗粒的几何尺寸和热物性均相同,且为全混式分布; 2)假设冷、热颗粒的发射率均为εr,且其内部的温度场均匀分布; 3)忽略颗粒间缝隙内气膜热阻的影响,认为气相为透明体。
由上述简化假设,根据热平衡定律,可求出以单个颗粒表面积为基准的辐射换热系数为:
(8)
式中:n—颗粒群特性参数,即每个颗粒被n个颗粒包围;εr—颗粒的发射率;σ0—斯忒藩-玻尔兹曼常数,W/(m2·K4);Tc,Th—冷、热颗粒的温度,K。
由式(6)~(8)可知,颗粒间的辐射换热系数与颗粒的直径无关,且几乎不受操作工况的影响,当增大操作气速时,床层空隙率εf和颗粒间距离s略有增加,颗粒群特性参数n和辐射换热角系数x(s)略有减小。
2.3.2 颗粒间导热模型 将反应器内颗粒间在接触处的导热和颗粒间缝隙内气膜的非稳态导热2种方式合并在一起讨论,建立颗粒间导热简化模型示意图如图3所示。
为了便于分析,简化假设:1)每个颗粒都被静止气膜包围,且气膜厚度δ与颗粒直径dp有关,一般取δ=(0.02~0.5)dp,本研究取δ=0.1dp;2)两个颗粒间的距离为l12,两个颗粒的半径分别为r1和r2,当l12>r1+r2+δ时,颗粒间的传热不计;当l12≤r1+r2+δ时,其传热不能忽略不计,其中,当r1+r2 图3 颗粒间导热简化模型示意图Fig.3 Simplified model of thermal conductivity of the particles 图4 颗粒间碰撞传热过程热阻Fig.4 Thermal resistance of the heat transfer process due to particle collision 根据图3和图4,可分别求出接触表面间的气隙导热热阻(式(9))、非接触表面间的静止气膜的热阻(式(10))和固体颗粒的内部热阻(式(11))。 (9) (10) (11) 根据图4所示的传热过程热阻串联、并联关系,可以推导出总热阻为: 2.4 二维对流换热模型的建立 根据反应器的流化工艺可知,在反应器内部存在热烟气与内胆壁和外筒壁间的对流换热,在内胆内部存在热流化气与内胆壁间的对流换热。为了简化分析,建立反应器内二维对流换热模型如式(13)所示,其中①为传热系数方程,②为连续性微分方程,③和④为动量微分方程式,⑤为能量微分方程式。 (13) 结合传热过程分析,反应器内涉及热流化气体(不凝气体)与内胆壁间、热烟气与内胆壁及外筒壁间的对流换热模型,均可通过将实验获得的不凝气体和热烟气的相关物性参数代入上述二维对流换热微分方程组进行联立求解,进而获得反应器内部不凝气和热烟气的温度随时间的变化规律。 图5 反应器耦合仿真简化模型Fig.5 Simplified model for reactor coupling simulation 3.1 仿真简化模型 为了便于进行仿真计算,将反应器中内胆与外壁间的热烟气加热方式简化为热壁面加热方式,简化的计算模型如图5所示。图中流化气体为不凝气体,入口条件为速度入口,速度为0.5 m/s,入口温度为573 K;出口条件为压力出口;床料为石英砂颗粒,粒径为0.3 mm,堆积高度为60 mm。 3.2 边界条件的设定 热边界条件选择对流换热和辐射换热耦合形式。仿真计算选用多相Eulerian模型,选择非稳态隐式分离求解器、标准紊流模型,并采用UDF编程对气固曳力系数、颗粒相间作用系数和固相应力进行自定义。 3.3 仿真结果与分析 为了考察反应器内部颗粒相和气相的温度分布以及热量传递情况,对传热模型进行仿真计算,得到不同时刻反应器壁面温度场和焓值分布情况如图6和图7所示;反应器内部床层中心处各相温度沿轴向高度的变化趋势如图8所示。 由图6和图7可以看出,计算初期由于颗粒相集中分布在中下部区域,因而反应器底部壁面的温度和焓值明显低于中部和顶部;随着计算逐渐趋于稳定,反应器壁面中上部区域逐渐和内部气相发生热量传递。 图8 反应器内部各相温度沿轴向高度变化趋势(5s)Fig.8 Temperature change trend along axial height of each phase in the reactor (5s) 从图8中可以发现,反应器内部各相的温度沿床高方向均逐渐升高,而且径向温度梯度逐渐趋于稳定,气体升温速率明显高于固体的升温速率;在回流区,由于气相体积浓度较大出现了局部温度较高,温度梯度较大;在反应器出口处,由于热载气被周围的冷空气带走,其温度明显下降;在床层高度0.3~0.4 m处固相颗粒已处于流态化,因此,有明显的气固换热。由平均温度变化曲线可知,此时基本满足生物质颗粒快速热裂解条件。需要指出该仿真计算并没有考虑生物质颗粒发生热化学反应的影响,得到的出口温度并不一定符合实际发生热裂解后的温度。因此,今后还需要进一步建立完整的耦合模型。 为了进行热量平衡校核,仿真计算5 s后,获得各相的热量情况如表1所示。由表1可知,仿真计算结果满足气固相散失的总热量等于混合相散失的总热量,说明该计算模型满足能量守恒定律。另外,该模型计算结果可以获得出口气相平均温度约为720 K。 表1 反应器内各相的热量情况(5s)Table 1 Heat situation of each phase in the reactor (5s) 结合现有流化床传热模型,针对自行设计的内胆式双热型生物质热解反应的流化工艺,通过对反应器内热量传递过程的分析,建立了该反应器的壁面传热模型、颗粒间传热模型和二维对流换热模型;并通过仿真分析对该传热模型进行了验证,得出该耦合仿真模型基本满足生物质颗粒快速热裂解条件,并预测出口气相平均温度约为720 K。 [1]VIJAY G N,REDDY B V.Effect of dilute and dense phase operating conditions on bed-to-wall heat transfer mechanism in a circulating fluidized bed combustor[J].International Journal of Heat and Mass Transfer,2005,48 (16):3276-3283. [2]周星龙,程乐鸣,夏云飞,等.600MW循环流化床锅炉水冷壁和中隔墙传热特性[J].中国电机工程学报,2014,34(2):225-230. ZHOU X L,CHENG L M,XIA Y F,et al.Heat transfer characteristic of water wall and partition wall in a 600 MW CFB boiler[J].Proceedings of the CSEE,2014,34(2):225-230. [3]李三平,王述洋,孙雪,等.新型内胆式双热型生物质热解反应器设计模型[J].林产化学与工业,2014,34(1):49-56. LI S P,WANG S Y,SUN X,et al.Design of liner type double heated biomass pyrolysis reactor[J].Chemistry and Industry of Forest Products,2014,34(1):49-56. [4]LEVESPIEL O,WALTON J S.Bed-wall heat transfer in fluidized systems[J].Chemical Engineering Progress Symposium Series,1954,50(9):1-13. [5]NOWAK W,ARAI N,HASATANI M,et al.Stochastic model of heat transfer in circulating fluidized bed[C]//4th SCEJ Symposium on Circulating Fluidized Bed.Tokyo:[s.n.],1991:19-26. [6]VIJAY G N,REDDY B V.Effect of dilute and dense phase operating conditions on bed-to-wall heat transfer mechanism in a circulating fluidized bed combustor[J].International Journal of Heat and Mass Transfer,2005,48(16):3276-3283. [7]国井大藏,列文斯比尔.流态化工程[M].华东石油学院,上海化工设计院,译.北京:石油化学工业出版社,1977:260-289. KUNII D,LEVENSOPIEL O.Fluidization Engineering[M].Translated by East China Petroleum Institute,Shanghai Chemical Design Institute.Beijing:Petroleum Chemical Industry Press,1977:260-289. [8]王立,倪学梓,冯旭.流化床与浸入表面间的传热机制[J].冶金能源,1992,11(1):51-56. WANG L,NI X Z,FENG X.Heat transfer mechanism between fluidized bed and immersed surface[J].Metallurgical Energy,1992,11(1):51-56. [9]黄文迪,许国良.气固流化床颗粒间辐射换热模型[J].华中理工大学学报,1996,24(1):12-16. HUANG W D,XU G L.Particle radiative heat transfer model in gas-solid fluidized bed[J].Journal of Central China University of Science and Engineering,1996,24(1):12-16. [10]郭雪岩,柴辉生,晃东海.大颗粒流化床传热数值模拟与气固传热模型比较[J].上海理工大学学报,2012,34(1):81-87. GUO X Y,CHAI H S,CHAO D H.Numerical simulation of large particle fluidized bed and comparison of gas-particle heat transfer models[J].Journal of University of Shanghai for Science and Technology,2012,34(1):81-87. [11]李锦时,孙巧群,王猛,等.流化床反应器内热动力特性的数值模拟[J].哈尔滨工业大学学报,2013,45(11):50-55. LI J S,SUN Q Q,WANG M,et al.Simulation of thermodynamics in a fluidized bed reactor[J].Journal of Harbin Institute of Technology,2013,45(11):50-55. Analysis of Heat Transfer Process of Liner Type Double Heated Biomass Pyrolysis Reactor LI Sanping, SUN Xue, WANG Shuyang (College of Electromechanical Engineering,Northeast Forestry University, Harbin 150040, China) Based on the analysis of heat transfer process of liner type double heated biomass pyrolysis reactor designed by the author, the heat mathematical models of reactor wall′s conduction heat transfer, heat transfer among particles and two-dimensional convective heat transfer were established according to the reactor′s complex internal heat transfer characteristics. This model contained a variety of heat transfer methods such as heat transfer between thermal bed material and biomass powder, heat convection of biomass powder and heat carrier gas, radiation heat transfer from the wall to biomass powder and bed material, etc. Finally, the heat transfer model was determined by simulation analysis. The simulation results show that the coupling simulation model can meet the requirement of rapid pyrolysis of biomass particles, and the average temperature of outlet gas phase is about 720 K. biomass pyrolysis;heat transfer process;heat transfer model;simulation 10.3969/j.issn.0253-2417.2017.01.009 2016- 03-30 中央高校基本科研业务费专项资金资助(2572014BB06) 李三平(1981— ),女,湖北汉川人,讲师,博士,主要从事生物质能技术的研究;E-mail:bluelii73@163.com TQ35;TK6 A 0253-2417(2017)01- 0073- 08 李三平,孙雪,王述洋.内胆式双热型生物质热解反应器内传热过程建模分析[J].林产化学与工业,2017,37(1):73-80. *通讯作者:孙 雪,副教授,硕士生导师,研究领域为生物能源技术与装备。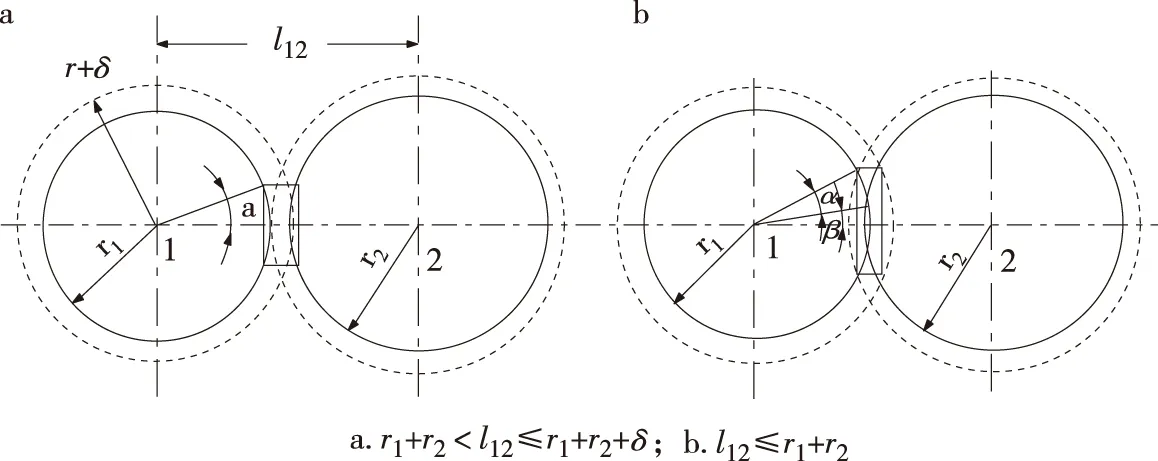



3 反应器内传热过程仿真分析




4 结 论

