结构参数单边变化对蜂窝芯弹性性能的影响

王冰松

（中车青岛四方机车车辆股份有限公司，山东 青岛266111）

0 引言

在目前国内动车组的地板等内装结构中，满足工字梁原理的蜂窝夹芯板已被广泛应用[1-2]。对于呈六边形的铝蜂窝芯子单元，其与水平方向呈θ角的4条边长为l，厚度为t，竖直方向的2条边长为h，厚度为2t，如图1所示。

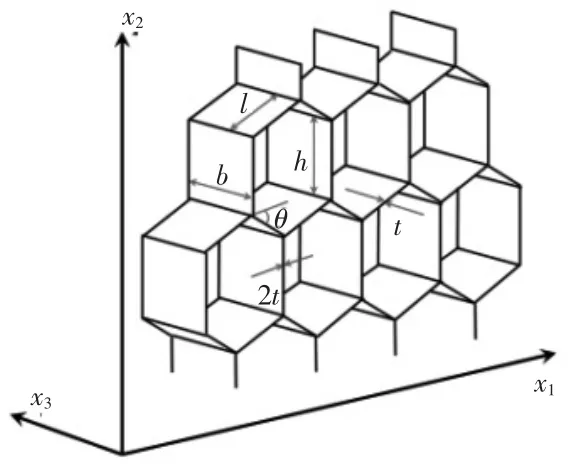
图1 铝蜂窝芯的结构尺寸

x3方向为异面方向，x1-x2面内为共面方向。蜂窝芯子相当于工字梁的腹板，需承受全部的剪切载荷。虽然目前对蜂窝芯弹性参数的求解已经有了较为成熟的解析理论[3-5]，但对于结构参数的变化所导致的芯子整体弹性性能影响的规律性结论却始终没有统一。故本文从h、l、θ和t的单边变化入手，得到参数变化所带来的影响规律。

1 共异面弹性常数的数学模型

本文利用Timoshenko理论和材料的小变形弹性假设，且认为胶接完好。对于动车组中常用的蜂窝芯，其壁厚与壁长的比值均可认为足够小。设蜂窝基体铝材的密度为ρs，则由Gibson理论可知，芯子整体密度为：

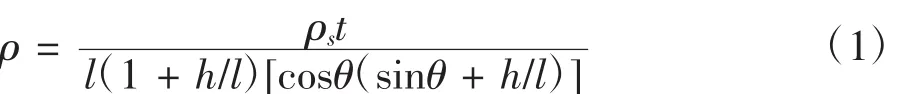
1.1 弹性模量的解析公式

如图2和图3所示，考虑共面方向的单轴压缩，远端应力σ使得蜂窝斜孔壁同时发生了弯曲、剪切和伸缩变形。根据力平衡条件及Timoshenko理论，并设基体铝材的弹性模量为ES，泊松比为vS，则可知共面方向上的弹性模量E1和E2分别为[6]：

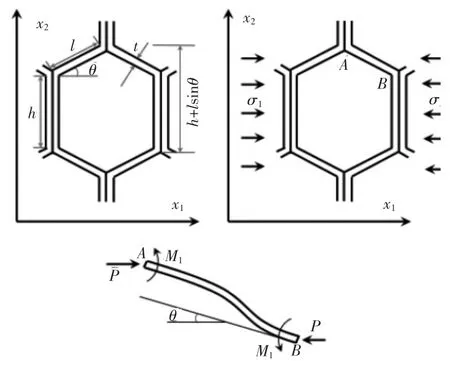
图2 蜂窝共面尺寸及1方向单轴受压变形

图3 蜂窝共面尺寸及2方向单轴受压变形

对于铝蜂窝芯的异面弹性模量E3，其值仅与等效前后的密度相关，即

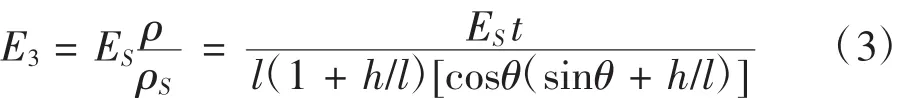
1.2 泊松比的解析公式

同样，在考虑了蜂窝壁的弯曲、剪切和伸缩变形之后，更新的面内泊松比解析公式为[6]：

注意到，蜂窝芯整体的泊松比v31和v32与基体铝材的泊松比vS相等，而v13和v23分别等于vSE1/E3和vSE2/E3.

2 结构参数对弹性性能的影响

2.1 R V E模型的建立

RVE法[7-8]在处理具有周期性结构的复合材料时具有计算的高效性。但对于铝蜂窝芯，RVE模型的尺寸选择便是一个首要问题。如图4所示，本节首先选择水平L方向分别包含有N=1、3、5、7和9个完整蜂窝格的模型，对共异面弹性模量结果进行收敛性分析。

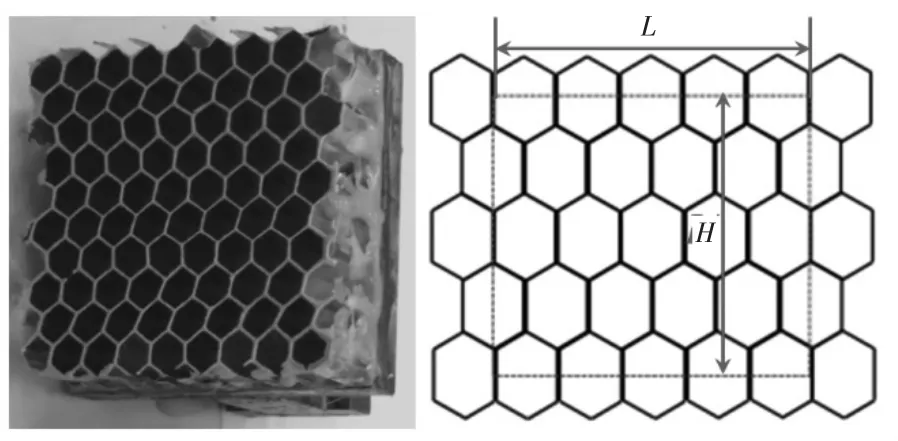
图4 铝蜂窝芯的周期型结构

经过对5类模型共15次仿真计算，共异面的弹性模量数值解结果分布如图6和7所示。对于E1，数值解随着格子数的增加而增大，且当格子数大于5时，开始超出试验解[6]的上限值。对于E2，数值解随着格子数的增加而上下浮动，但当N=1时超出了试验解的上限值。对于E3，数值解随着格子数的增加而始终保持平稳，且未超出试验解的上限值。再结合得到的解析解并考虑计算经济性，最终选择N=5的RVE模型，使用S4R壳单元进行网格划分，如图5所示。共异面方向的三类边界条件如表1～3所示。

图6 E1、E2的数值解与解析和试验解对比

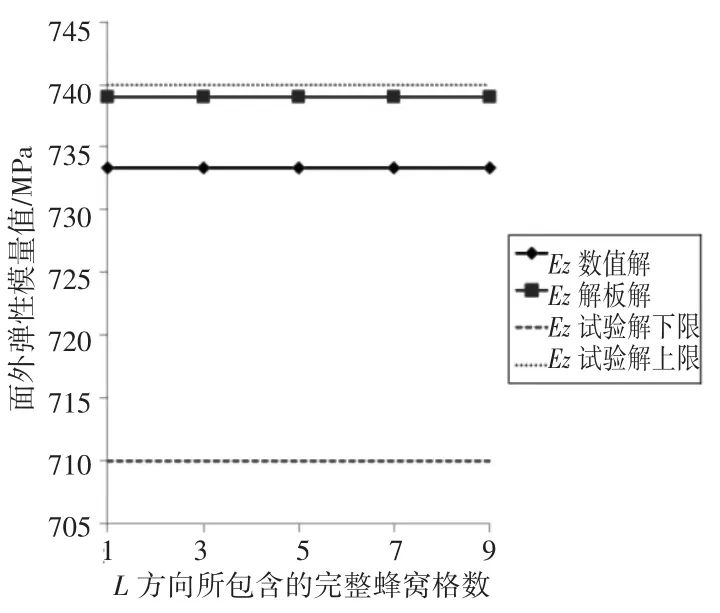
图7 E3的数值解与解析和试验解对比

表1 E1数值求解的边界条件

表2 E2数值求解的边界条件

表3 E3数值求解的边界条件

2.2 弹性模量的变化规律

由式（2）、（3）可知，弹性模量均与 h、l、θ和 t相关。本节主要关注的是这四个参数单独变化，即发生单边变化时带来的弹性性能的影响。由于在上一节建立的RVE模型的准确性已经被试验数据所验证，所以本节使用该模型，首先计算的是面内弹性模量的变化趋势，结构参数的变化情况为：h=1～10，Δ ＝ 1；l＝ 1～10，Δ ＝ 1；θ＝ 1～80°，Δ ＝ 10°；t＝ 0.03～0.085，Δ＝0.005.为了避免重复，h＝l＝6和θ＝30°的情况不作计算。

如图8～图10所示，随着胞壁边长h和l以及倾角θ的增长，E1呈现出下降趋势。尤其是在l和θ的变化初期，下降程度非常剧烈。如图11所示，E1会随着胞壁厚度的增加而增大。对于E2、l和t对其的影响规律与E1一致，但随着h和θ的增加，E2会表现出增长趋势。根据最小二乘法进行拟合，得到E2和E2的规律性公式，即

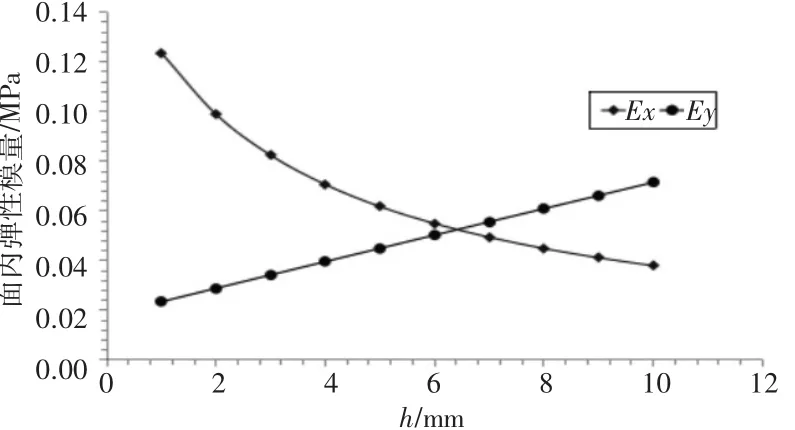
图8 面内弹性模量随变化的曲线图

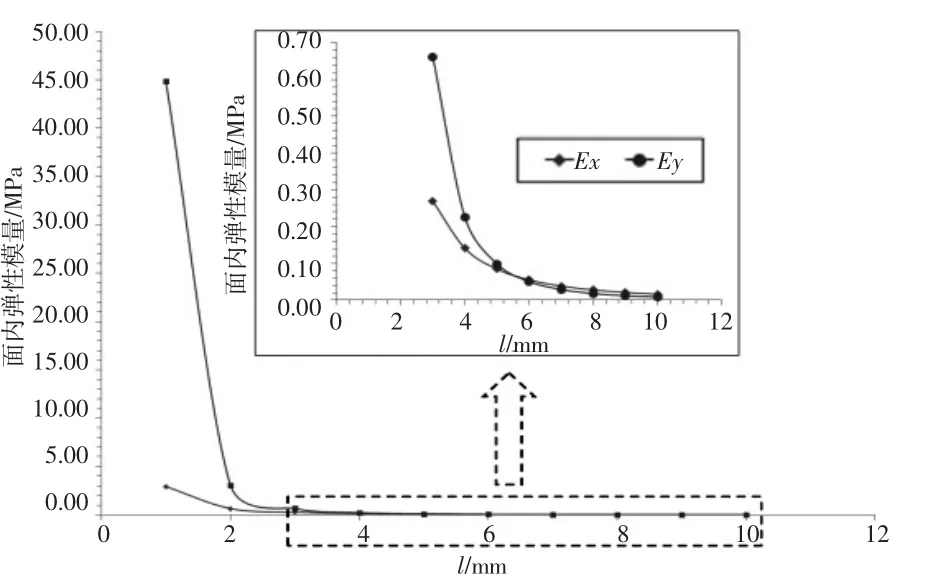
图9 面内弹性模量随变化的曲线图

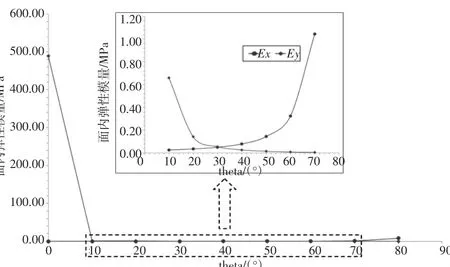
图10 面内弹性模量随变化的曲线图

图11 面内弹性模量随变化的曲线图

由图12～图15可知，面外弹性模量E3会随着胞壁边长h和l的增加而降低。但相反的情况会出现在随t变化的曲线上，而随着θ的增大，E3会在微弱降低后逐渐增加。根据最小二乘法对所得曲线进行拟合，得到相应变化范围内E3的规律性公式，即

图12 面外弹性模量随变化的曲线图

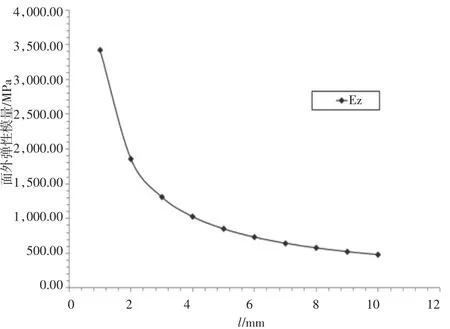
图13 面外弹性模量随变化的曲线图

图14 面外弹性模量随变化的曲线图

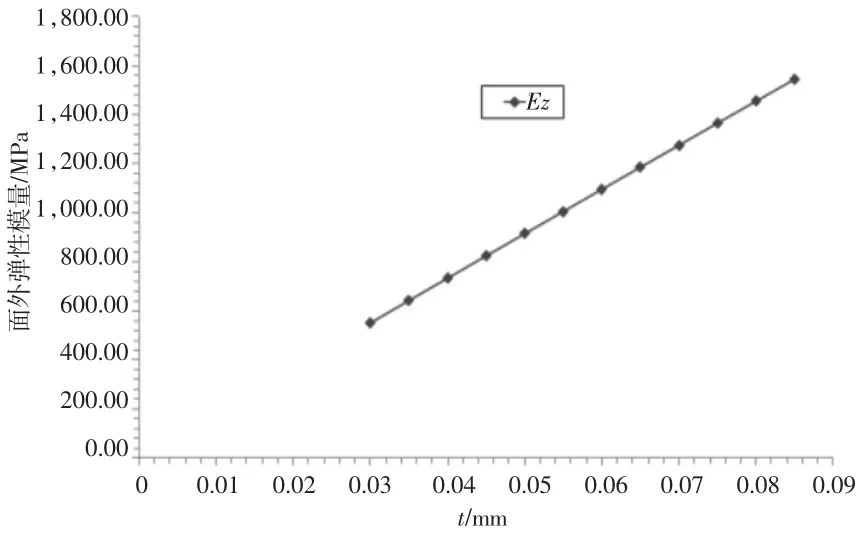
图15 面外弹性模量随变化的曲线图

2.3 泊松比的变化规律

利用所建立的RVE模型，本节对泊松比受与2.2节相同的变化条件影响下表现出的规律进行了研究。通过数值结果可以发现：对于v31和v32，数值基本不变，均与基体铝材的泊松比相同，即0.34；对于v13和v23，数值基本稳定在近似于0的范围内；而对于v12和v21，当h、l和θ发生变化时，二者的数值则会发生较为明显的波动，见图16和图17，而对壁厚t的变化并不敏感。

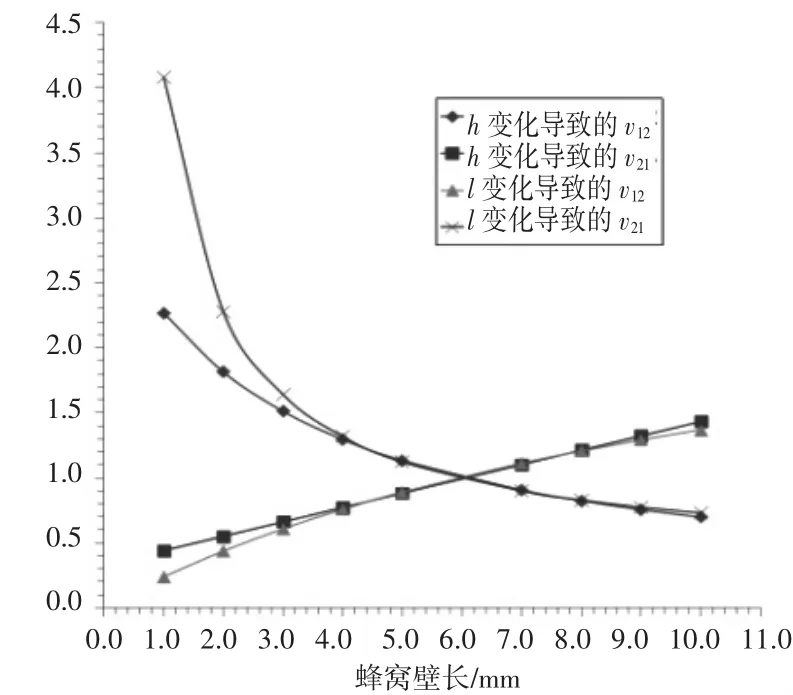
图16 和受蜂窝壁长和的影响规律

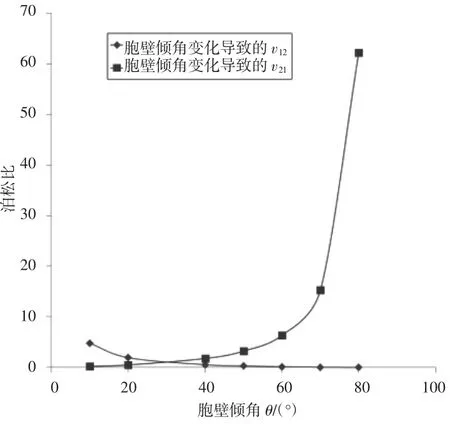
图17 和受蜂窝壁长的影响规律

根据最小二乘法对所得曲线进行拟合，得到相应变化范围内v12和v21的规律性公式，即

3 结束语

本文以中国标准动车组的客室地板铝蜂窝芯结构为对象，建立了RVE表征模型，通过收敛性分析并结合试验数据，验证了模型的准确性。其次，从h、l、θ和t四个结构参数的单边变化入手，得到了参数变化所带来的影响规律，即

1）面内弹性模量E1和E2受结构参数的影响均较为明显，波动幅度的数量级为10-1～10-2；

2）面外弹性模量E3受结构参数的影响更加明显，波动幅度的数量级为102；

3）泊松比v12和v21对h、l和θ的变化较为敏感，而壁厚t的变化对其的影响不大；

4）泊松比v31和v32始终保持与基体铝材的泊松比相同，而对于v13和v23，数值则基本稳定在近似于0的范围内。

同时，本文对四类计算的结果也进行了归纳，初步建立了蜂窝芯结构的材料属性库，并通过最小二乘法对各个弹性常数在常用设计范围内进行了经验公式的推导，利用这些公式，可以直接得到相应尺寸蜂窝芯的弹性参数而无需重新进行有限元计算，这也为今后蜂窝结构的设计优化工作提供了数值依据。

[1]蔡 茂，高 群，宗志坚.铝合金蜂窝结构轴向压缩吸能特性[J].材料科学与工程学报，2015，33（5）：23-25.

[2]庄守兵，吴长春，冯淼林，等.基于均匀化方法的多孔材料细观力学特性数值研究[J].材料科学与工程学报，2001，19（4）：9-13.

[3]Lorna J.Gibson，Michanel F.Ashby.Cellular Solids：Struc ture and Properties[M].Oxford：pergamon，1988.

[4]Shi G，Tong P.Equivalent transverse shear stiffness of hon eycomb structure[J].Composite Structures，2006，19（3）：177-183.

[5]Guo X，Gibson L.Behavior of intact and damaged honey comb：A finite-element study[J].Int JMech Sci.1999，41（11）：85-105.

[6]孙德强，张卫红，孙玉瑾.蜂窝铝芯的弹性模量和材料效率分析[J].力学与实践，2008，30（1）：35-40.

[7]王 瑞，王建坤，武 玲.平纹织物复合材料的弹性模量预测[J].复合材料学报，2002，19（1）：90-94.

[8]吴志凯，江五贵，郑 隆.界面对双向纤维增强复合材料力学性能的影响[J].复合材料学报，2017，34（1）：70-75.