两种求解连续体撞振响应方法对比研究

李丙涛，徐文涛，刘 磊，卫洪涛

（1.煤炭工业郑州设计研究院股份有限公司，郑州 450007；2.郑州大学 力学与工程科学学院，郑州 450001；3.西北工业大学 航天学院，西安 710072）

两种求解连续体撞振响应方法对比研究

李丙涛1，徐文涛2，刘 磊3，卫洪涛2

（1.煤炭工业郑州设计研究院股份有限公司，郑州 450007；2.郑州大学 力学与工程科学学院，郑州 450001；3.西北工业大学 航天学院，西安 710072）

力积分法和振型转换法是处理连续体撞振问题的常用方法。虽然作者已在前期提出了相对振型转换法，进一步扩展了传统振型转换法的适用范围，但尚未对其与力积分法求解结果差异进行深入研究。文章分别采用力积分法和相对振型转换法对基于工程背景的实际算例进行了数值求解，进而通过一种差异指标研究了刚度、阻尼对求解结果差异的影响。将上述两种方法与现有实验数据进行对比，结果表明，刚度增大与阻尼减小均会导致两种方法的分析结果差异增大，尤其当刚度提高到一定程度，即撞振为刚性撞击时，需要与实验结果对比确定仿真的正确性。对比两种方法数值求解过程可以发现，力积分法易于数值实现，而相对振型转换法具有计算效率高、收敛性好等优点。

连续体撞振；力积分法；相对振型转换法；非线性振动

0 引言

带阻挡的连续体振动研究在许多领域都受到关注，如原子力显微镜测量件的振动[1]、核反应堆管道振动[2]、机械齿轮接触问题[3]等。此类问题常简化为端点带阻挡或两端固支中间带阻挡的梁振动问题，研究的关键是在完整的振动周期中对梁的碰撞过程进行建模。金栋平等认为以往的研究方法可以分为“间断分析”和“连续分析”[4]，其中恢复系数法（coefficient of restitution, CoR）忽略碰撞过程时间，属于“间断分析”，该法适用广泛但在碰撞系数的取值上存在争议[5]。最近，Vyasarayani提出了一种能量连续的、可用于连续体的改进CoR方法[6]。考虑碰撞过程时间的分析方法属于“连续分析”，包含如下两类[7]。

1）力积分法（force integration method, FIM）：将接触分离的过程体现在外力上。该法视阻挡为刚度很大的弹簧，当连续体与阻挡接触时，将阻挡力体现在振动方程中。应用该方法对撞振问题进行研究的文献有[8-10]。也有观点认为CoR法本质上也是一种力积分方法，因其并没有改变接触前后方程采用的振型[11]。

2）振型转换法（mode transfer method, MTM）：将接触分离的过程体现在振型切换上。以端点带限制的悬臂梁为例，接触前系统采用悬臂梁振型，接触后采用带限制梁振型。应用该方法对撞振问题进行研究的文献有[12-14]。经典的振型转换法只能处理边界条件较为简单的、碰撞前后为线性的系统[11]。卫洪涛等在对其进行改进的基础上，提出了相对振型转换法（relative mode transfer method, RMTM），拓展了振型转换法的适用范围[15]。

利用FIM和MTM研究实际问题时，需要进行适当的模态截断。若采用单模态近似，并不能充分反映复杂系统的动力学特性；而采用多模态近似必然会耗费巨大的计算量，并带来收敛困难等诸多问题；尤其是当阻挡刚度足够大，系统撞击为刚性时，FIM和MTM求解时均要采用非常小的积分步长系统才能收敛，并得到差异较大的结果。前人对上述方法的优劣有一些定性的描述，如：Tsai最早对这两种方法进行了划分[7]，并对力积分法与振型转换法进行了初步对比，认为当阻挡刚度较大时，振型转换法具有收敛速度上的优越性；文献[16]认为CoR法在研究撞击时间短、表面硬的情况时适用，而力积分法能更精确描述实际的撞振过程；文献[17]分析了力积分法与 CoR法在研究“软碰撞”及“硬碰撞”时的适用性问题，认为对于非刚性碰撞，CoR法由于忽略了撞击接触的时间，会得到错误的结果；文献[18]认为CoR法将撞击接触时间设定为无限小是“存疑”的，同时该法会给接触过程的响应结果引入高频颤振，与之相比，力积分法更正确；文献[19]认为CoR法对实际撞振能量的耗散只是大致近似；文献[20]认为力积分法适合“柔性”阻挡情况，当发生刚性撞击时，力积分法仿真时间会增大。但是目前并没有上述两种方法与相对振型转换法的系统性对比研究。

本文分别利用力积分法与相对振型转换法对一种悬臂梁撞振模型进行研究，讨论参数对响应的影响，分析不同参数设置下，两种方法的计算效率，对比不同方法得到的结果与实验数据的差异。

1 研究方法描述

本文的研究对象如图1所示，悬臂梁端点有间隙大小为∆的阻挡，将其近似为线性弹簧，系统固支端带有底座运动w0(t)。

首先对梁在无撞振情况下进行建模，有

式中：ρ为梁密度；A为梁横截面积；E为弹性模量；I为惯性矩。此时边界条件为

梁上任意一点的位移可表示为模态叠加的形式，即

式中：φn(x)为第n阶振型函数；a(t)为模态坐标。将式(3)代入式(2)，有

将振型函数写成如下形式：

将式(4)代入式(5)，令A=1，可得第n阶振型函数φn(x)的表达式为

由模态振型的正交性：

将式(3)代入式(1)，方程两边同乘以φn后在[0,L]上进行积分，得到N阶离散偏微分方程组为

这样可以求出无接触情况下系统方程的精确解析解。

1.1 相对振型转换法

在一个振动周期中，假设系统从静止开始振动，t0时刻为初始时刻，梁上任意一点横向位移可以表达为w(x,t)=w1(x,t)。令t1时刻开始，端点位移大于间隙，系统将受到端点阻挡的反力作用，边界条件发生了变化，从而使得梁的振型也发生改变，此时梁上任意点的横向位移可看作边界条件转换前的位移叠加转换后的位移，即w(x,t)=w1(x,t1)+w2(x,t)。由此类推至系统边界条件改变的ti时刻，梁上任意点的横向位移为

式中φni(x)为ti-1～ti时间此边界条件下梁的第n阶振型；ani(t)为相应的模态坐标。将式(11)代入梁的振动方程中，可得ti-1～ti时刻梁的运动方程为

将式(12)代入式(13)，利用振型的正交性，可得离散后的N阶偏微分方程为

式中：tr为边界条件发生改变的时刻点；。状态转换时，振动方程的初值为，从而各阶模态位移的初值也为 0，模态速度有，这样有第n阶模态速度的表达式为

式中：φPi-1(x)=0表示时刻系统第P阶模态振型；为相应的模态速度。

相对振型转换法与经典振型转换法[7]最大的区别在于，对撞击前后系统任意点的位移表达不同。相对振型转换法的基本思想是：在每次发生振型转换时，将当前连续体系统的“形态”记录下来，引入“相对”的概念，转换后系统的振动看作是相对于转换前形态的“增量”运动，这也是相对振型转换法命名的由来。运用这一思想即得到系统位移的表达式(11)。而经典振型转换法仅仅是记录转换前后的各阶模态位移，在下次转换时代入上次转换前的记录值进行处理。以图1所示系统为例，假设t1时刻系统从悬臂梁状态转换为受限梁状态，t2时刻系统从受限梁状态转换回悬臂梁状态。用相对振型转换法研究时，系统状态转换前后的位移表达式用式(11)表达。而用经典的振型转换法研究时，首先记录时刻各阶模态位移，时刻系统转换到新的运动状态，各阶模态位移初值置0，有

当t2时刻系统重新由受限运动状态进入悬臂梁状态时，将上次状态转换前记录的各阶模态位移值回代，

上述经典振型转换法步骤对于更复杂的边界条件改变，如迟滞非线性边界条件以及可以离散为分段线性的边界条件问题，将不再适用，但是相对振型转换法仍然可以进行求解[15]。

1.2 力积分法

系统的运动方程有：

其中：δ(x-l)为狄拉克函数；Vcon(x,t)为接触力，即

式中k为阻挡刚度。利用伽辽金法对式(19)进行离散，令其解为

其中φn(x)取悬臂梁振型。代入系统参数，利用数值方法进行求解，即可得到梁上任意点的响应。

2 数值仿真

算例参数如表1所示，采用数值仿真求梁端点的时程响应。由于不同的方法得到的结果差异对阻挡刚度k以及阻尼比ξ最敏感，因此本文研究在这2种参数不同的情况下应用FIM和RMTM得到的结果的差异。

文献[21]定义了参数k*=k/(3EI/L3)，当k*分别为 5、5000时系统分别处于“软碰撞”及“硬碰撞”状态。本文分别考虑k*=0.13～13 000时研究结果的不同，如图2，其中y=0线表示阻挡位置。

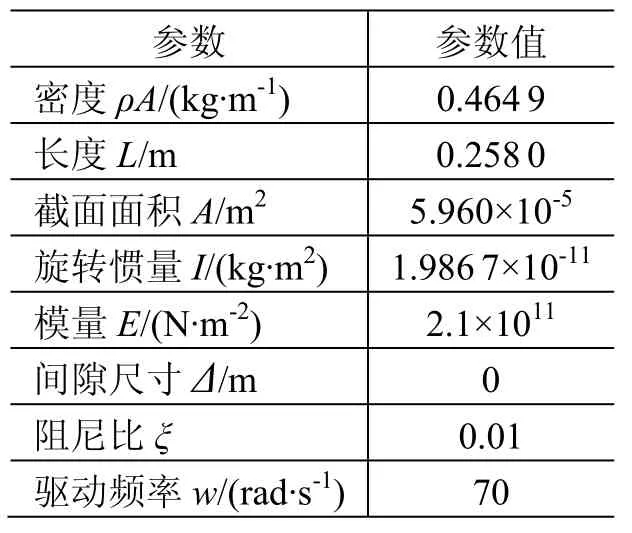
表1 系统参数Table 1 System parameters

从图2中可以看出：随着阻挡刚度的逐渐增大，梁端点在与阻挡碰撞后，与阻挡“黏”在一起运动的时间逐渐缩短，即梁端点位移为负值的时间逐渐缩短；当阻挡刚度较小时，两种方法得到的时程响应差别较小，随着阻挡刚度的增大，时程响应差异逐渐增大。因此需要调整阻尼大小并与实验结果对比来确定结果的正确性。

可以看出，差异指标随着刚度的提高而逐渐增大，但并不是线性增大。从阻尼比ξ=0.01得到的结果看，差异指标增加分为3个阶段：刚度k≤1×102N/m时，差异指标较小，都是 10-3量级；当刚度 1× 103N/m≤k≤1×105N/m时，指标增大到10-1量级；当刚度k≥1×106N/m，即系统处于“硬碰撞”状态时，两种方法之间的差异急剧增大到≥0.4，这从图2(c)中也可以看出，两个曲线之间已经有了较大的偏差。哪种方法更精确需要与实验数据进行对比确定。

表2 刚度及阻尼对结果影响差异指标Table 2 Different indexes with different stiffnesses and damping ratios

研究阻尼对结果差异的影响，有ξ=0.05时端点时程响应如图3。可以从表2看出，此时差异指标增大同样可以分为3个阶段，可见阻尼增大并没有改变结果差异随刚度增大而增大的趋势。

但是，在大阻尼条件下，阻挡刚度相同时不同方法得到的结果差异减小，见图4。值得注意的是，有如图4中ξ=0.01、k=1×103N/m的点，让整条差异曲线比较曲折，其原因是统计取点时，取结果相差较大的点较多，导致差异指标值较前后点相差较大。

为了对比两种方法的计算效率，利用MatLab/m文件进行编程实现，均采用4阶龙格库塔法；精简程序，排除由于编程引入的差异，其中：1）利用不同方法进行仿真时，循环均采用MatLab 标准循环命令，并且尽量减少循环，同时认为最后不可避免的循环语句是不同方法必然要承担的开销；2）两种方法都没有进行矢量化编程处理；3）两种方法进行编程时，都对循环时数组大小会改变的量进行了预分配内存。不同刚度及阻尼情况下，系统仿真0.2 s真实过程需要的时间开销，步长取 1×10-7，结果见表3。不同硬件配置的机器用时会与表中时间不同。

从表3可以看出：相同的参数设置，力积分法用时多，意味着相对振型转换法的计算效率高；力积分法用时会随着阻挡刚度增加而增大，而相对振型转换法用时基本相同。这是由于当刚度较大时，力积分法的方程中引入了较大的积分常量，导致利用 4阶龙格库塔法求解每一步步长耗时比小刚度时要大。还可以看出，当阻尼增大时，两种方法用时均随之增加。

3 实验结果对比

采用与文献[22]中相同的参数设置，为了简便这里取均质规则梁。分别应用FIM和RMTM求端点的时程响应，并与文献中实验数据对比，结果见图5。图中，下部的余弦曲线（u）是底座位移曲线，而上部的曲线（y）是梁端点相对于底座的位移响应。仿真时，为了快速达到稳态，统一采用较大的阻尼比ξ=0.05。

由于设置了均质规则梁，而文献中梁端点带有半球形质量块，因此同样的激励频率下，图5(b)、(c)与图5(a)相比，波峰形态略有不同，而波峰峰值以及撞击发生于激励力曲线的相位相近。同时可以看到，图5(b)与(c)相似度较高，两种方法得到的时程响应基本类似。需要注意的是，力积分法得到的结果中，梁端点与底座接触时不会“黏滞”在一起，如图5(b)表现出“颤振”形态；而相对振型转换法则表现出“黏滞”在一起振动的形态，后者更贴近实际[18]。

4 结论

1）刚度对FIM和RMTM的结果差异有较大影响，且随着刚度的增大，结果差异也会随之增大。当阻挡刚度较大，即系统处于“硬碰撞”时，两种方法产生较大的差异，需要与实验数据对比以确定得到结果的正确性。

2）阻尼对两种方法求解结果的差异影响不可忽略，阻尼增大能显著降低结果差异，但是增大阻尼并不会改变差异随刚度增大而增大的趋势。

3）仿真时，采用相同的仿真环境及参数设置，力积分法用时较长，即力积分法的计算效率较低。

4）大刚度时，相对振型转换法得到的端点与阻挡接触时的时程响应与实际情况更一致，即相对振型转换法更贴近实际。

综上，力积分法不需要计算额外的复杂边界条件下的振型，对于复杂问题有操作便利性；但是相对振型转换法具有更好的收敛性和计算效率。大刚度条件下相对振型转换法得到的结果更贴近实际。同时发现，大刚度时，阻尼对仿真收敛以及两种方法得到的时程响应差异的影响较大，仍需要与实验结果相类比以确定哪种方法能更好地描述撞振过程，这是下一步要做的工作。

端点带阻挡的悬臂梁所代表的这一类撞振问题具有广泛的工程背景，对于航天领域，在研究非线性连接对航天器动力学响应影响时，连接带间隙的结构振动问题可以归类为撞振问题。在研究此类问题时，基于振型转换的方法和力积分法是两类常用的方法，以往的工作对两种方法的认识局限于定性，本文得到的结论弥补了以往工作的空白。

（References）

[1]朱杰, 孙润广.原子力显微镜的基本原理及其方法学研究[J].生命科学仪器, 2005, 3(1): 22-26 ZHU J, SUN R G.Introduction to atomic force microscope and its manipulation[J].Life Science Instruments, 2005, 3(1): 22-26

[2]KNUDSEN J, MASSIH A R.Vibro-impact dynamics of a periodically forced beam[J].ASME Journal of Pressure Vessel Technology, 2000, 122(2): 210-221

[3]THEODOSSIADES S, NATSIAVAS S.Periodic and chaotic dynamics of motor-driven gear-pair system with backlash[J].Chaos Solitons & Fractals, 2001, 13(12): 2427-2440

[4]金栋平, 胡海岩.碰撞振动及其典型现象[J].力学进展, 1999, 29(2): 12-21 JIN D P, HU H Y.Vibro-impact and their typical behaviors of mechanical systems[J].Advances in Mechanics, 1999, 29(2): 12-21

[5]姚文莉, 岳嵘.有争议的碰撞恢复系数研究进展[J].振动与冲击, 2015, 34(19): 43-48 YAO W L, YUE R.Advance in controversial restitution coefficient study for impact problems[J].Journal of Vibration and Shock, 2015, 34(19): 43-48

[6]VYASARAYANI C P, MCPHEE J, BIRKETT S.Modeling impacts between a continuous system and a rigid obstacle using coefficient of restitution[J].ASME J Appl Mech, 2009, 77(2): 021008

[7]TSAI H, WU M K.Methods to compute dynamic response of a cantilever with a stop to limit motion[J].Computers & Structures, 1996, 58(5): 859-867

[8]LIN W, QIAO N, YUYING H.Bifurcations and chaos in a forced cantilever system with impacts[J].Journal of Sound and Vibration, 2006, 296(4): 1068-1078

[9]游斌弟, 潘冬, 赵阳.关节铰间隙对漂浮基星载天线扰动研究[J].宇航学报, 2010, 31(10): 2251-2258 YOU B D, PAN D, ZHAO Y.Research on disturbance of joints with clearance on free-floating satellite antenna[J].Journal of Astronautics, 2010, 31(10): 2251-2258

[10]钱震杰, 章定国.含摩擦碰撞柔性机械臂动力学研究[J].振动工程学报, 2015, 28(6): 879-886 QIAN Z J, ZHANG D G.Frictional impact dynamics of flexible manipulator arms[J].Journal of Vibration Engineering, 2015, 28(6): 879-886

[11]VYASARAYANI C P.Transient dynamics of continuous systems with impact and friction, with applications to musical instruments[D].Waterloo: University of Waterloo, 2009

[12]BRAKE M R, WICKERT J A.Modal analysis of a continuous gyroscopic second-order system with nonlinear constraints[J].Journal of Sound and Vibration, 2010, 329(7): 893-911

[13]ERVIN E K, WICKERT J A.Repetitive impact response of a beam structure subjected to harmonic base excitation[J].Journal of Sound and Vibration, 2007, 307(1): 2-19

[14]BRAKE M R.A hybrid approach for the modal analysis of continuous systems with discrete piecewise-linear constraints[J].Journal of Sound and Vibration, 2011, 330(13): 3196-3221

[15]卫洪涛.带非线性连接及限制连续体动力学建模方法及响应研究[D].哈尔滨: 哈尔滨工业大学, 2012

[16]FOALE S, BISHOP S R.Bifurcations in impact oscillations[J].Nonlinear Dynamics, 1994, 6(3): 285-299

[17]BLAZEJCZYK-OKOLEWSKA B, CZOLCZYNSKI K, KAPITANIAK T.Hard versus soft impacts in oscillatory systems modeling[J].Communications in Nonlinear Science and Numerical Simulation, 2010, 15(5): 1358-1367

[18]SZALAI R.Impact mechanics of elastic structures with point contact[J].Journal of Vibration and Acoustics, 2014, 136(4): 041002

[19]MELCHER J, CHAMPNEYS A R, WAGG D J.The impacting cantilever: modal non-convergence and the importance of stiffness matching[J].Philosophical Transactions of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, 2013.DOI: 10.1098/rsta.2012.0434

[20]VYASARAYANI C P, SANDHU S S, McPHEE J.Nonsmooth modeling of vibro-impacting Euler-Bernoulli beam[J].Advances in Acoustics and Vibration, 2012.DOI: 10.1155/2012/268595

[21]RAHMANI A M, ERVIN E K.Frequency response of an impacting lap joint[J].Journal of Nonlinear Dynamics, 2014(6).DOI: 10.1155/2014/310834

[22]VAN DE VORST E L B, HEERTJES M F, VAN CAMPEN D H, et al.Experimental and numerical analysis of the steady state behaviour of a beam system with impact[J].Journal of Sound and Vibration, 1998, 212(2): 321-336

（编辑：许京媛）

A comparative study of two methods for determining the vibration response of vibro-impact continuum

LI Bingtao1, XU Wentao2, LIU Lei3, WEI Hongtao2
(1.Zhengzhou Design and Research Institute of Coal Industry Co., Ltd, Zhengzhou 450007, China; 2.School of Mechanics and Engineering Science, Zhengzhou University, Zhengzhou 450001, China; 3.School of Astronautics, Northwestern Polytechnical University, Xi’an 710072, China)

The force integration method(FIM) and the mode transfer method(MTM) are two kinds of frequently-used methods to solve the vibro-impact problem of continuum.In a previous paper, the authors put forward the method of the relative mode transfer method(RMTM), and expanded the application scope of MTM, but the differences of numerical results obtained from the FIM and the RMTM remain to be explored.With an example of practical engineering background, the numerical results are obtained both through the FIM and the RMTM.An index for evaluating the difference of the results is proposed, and the effects of the stiffness and the damping ratio on the index are discussed.Finally the results are compared with the experimental data from literature, and it is indicated that the increase of the stiffness and the damping ratio leads to the increase of the difference index.The correctness of the simulation result using the two methods is determined by comparing with experimental data when the stiffness is increased to a certain degree which makes the impact become a rigid impact.By comparing the numerical process of the two methods, it is shown that FIM is more convenient to obtain the results but RMTM enjoys a better convergence and a higher calculation efficiency.

vibro-impact continuum; force integration method; relative mode transfer method; non-linear vibration

V414

：A

：1673-1379(2017)01-0021-07

10.3969/j.issn.1673-1379.2017.01.004

卫洪涛（1982—），男，博士学位，从事结构振动测试与分析研究。E-mail: htwei@zzu.edu.cn。

2016-06-02；

：2017-01-23

河南省高等学校重点科研项目计划（编号：15A130006）；国家自然科学基金（编号：11402044）；中央高校基本科研业务费3102015BJ(11)MYZ16

李丙涛，徐文涛，刘磊，等.两种求解连续体撞振响应方法对比研究[J].航天器环境工程, 2017, 34(1): 21-27

LI B T, XU W T, LIU L, et al.A comparative study of two methods for determining the vibration response of vibro-impact continuum[J].Spacecraft Environment Engineering, 2017, 34(1): 21-27