三轴振动试验系统工作平台的谐振频率分析

周兴广，田振强，王 冰，秦亚明，贺智国

（北京强度环境研究所，北京 100076）

三轴振动试验系统工作平台的谐振频率分析

周兴广，田振强，王 冰，秦亚明，贺智国

（北京强度环境研究所，北京 100076）

为验证并提高三轴振动试验系统工作平台的谐振频率，进而提高系统的工作频率范围，文章采用有限元软件对平台在自由状态下的模态进行仿真。比较仿真结果与三轴振动试验结果可以看出，对角和对边弯曲频率偏差较小。该结果可为后续设计工作提供相对精确的计算指导。

三轴振动试验系统；工作平台；动态特性；谐振频率；仿真分析

0 引言

航天器入轨前受到的力学激励是多个方向同时作用的复杂振动环境。试验表明，多轴振动试验系统能够更真实地模拟实际的动力学环境，在产品故障模式复现和模拟精度方面具有显著的优势；一些已通过单轴振动测试的产品再进行多轴振动试验，还会暴露出新的故障，而这些故障模式在实际使用过程中也出现过[1-2]。因此对于大多数航天器来说，多轴振动试验有助于提高其使用可靠性[3-4]。

三轴振动试验系统的工作平台作为试件的载台，可实现3个正交方向的合成运动。因此，在三轴振动试验系统的设计中，平台的结构优化和仿真计算起着至关重要的作用，而系统的关键技术指标“最高使用频率”与平台的共振频率有直接关系[5]。同时，三轴振动的测试结果能够有效验证仿真设计的正确性，为后续设计工作提供有效支撑[6]。

传统工作平台的模态分析基本是单向振动或多轴低频振动，即主要针对一阶轴向共振频率进行仿真计算，无法验证弯曲模态对系统特性的影响。本文首先对三轴振动试验系统的工作平台进行有限元建模和模态分析，仿真计算弯曲频率；然后，将结果与三轴振动试验结果进行对比分析，以验证仿真结果的正确性，以期提升三轴振动试验系统仿真计算对设计工作的指导作用。

1 工作平台数值分析

1.1 工作平台结构

三轴振动试验系统主要包括振动台、工作平台、解耦装置、对中装置、多维控制器、数据采集及测试子系统。

与单方向振动的扩展台面不同，三轴振动试验系统的工作平台要将3个振动台产生的能量同时传递给试件，因此工作平台设计的基本要求有：1）能方便地将平台同时与3个振动台连接；2）平台质量要小，3个方向刚度都要大，自身固有频率要尽量高；3）尽量采用铸件加工，各方向阻尼特性好，不易发生局部共振[7-8]。

设计的工作平台为外形尺寸600 mm×600 mm× 200 mm的筋板状结构（见图1）。由于工作平台同时要满足三轴振动的工作频率需要，这要求有较高的刚度和质量比值，所以采用镁合金整体铸造加工工艺，底部采用蜂窝状结构（见图2）。平台上表面用以安装试件，侧面用以连接2个水平正交振动台的解耦装置，下表面用以安装垂直振动台方向上的解耦装置。

1.2 工作平台模态分析

自由模态分析和施加约束的模态分析都是模态分析的重要内容。自由模态是结构自由振动的固有特性，只与结构本身相关，而与外界激励和约束条件无关。实际环境的结构振动是其模态振型或某几阶或多阶振型的叠加振动。在平台的模态分析和测试中，由于约束载荷、连接刚度以及外界激励很难量化，一般选择自由模态分析。

仿真计算时，首先建立工作平台的有限元分析模型。划分网格时考虑平台的结构特征，选用8节点六面体单元类型。材料选择弹性体镁合金，弹性模量为4.5×1010Pa，泊松比为0.35，密度为1800 kg/m3，总质量52 kg。图3为工作平台的有限元模型，共包含 12 243个单元。本文选用有限元分析软件ANSYS对工作平台进行模态分析，分析时采用Block Lanczos模型提取方法，且不施加边界条件与约束。在划分网格和模态分析过程中，由于上表面和侧面的安装螺纹孔、各筋板铸造倒角和圆角的质量很小，对模态影响很小，若在计算过程中对这些局部进行网格化则会占用大量计算时间，所以计算过程中不予考虑。

表1列出计算所得平台各阶共振频率数值。由于处于无约束状态，平台前6阶模态为无约束状态下6个自由度的平动频率，均为0 Hz；第7阶模态为平台对角一阶弯曲频率（见图4），对角弯曲频率为777.6 Hz；第8阶模态为平台对边一阶弯曲频率（见图5），对边弯曲频率为1 752.4 Hz，其余各阶频率均为各边角的翘起或扰动，对系统影响不大，故本文不予考虑。

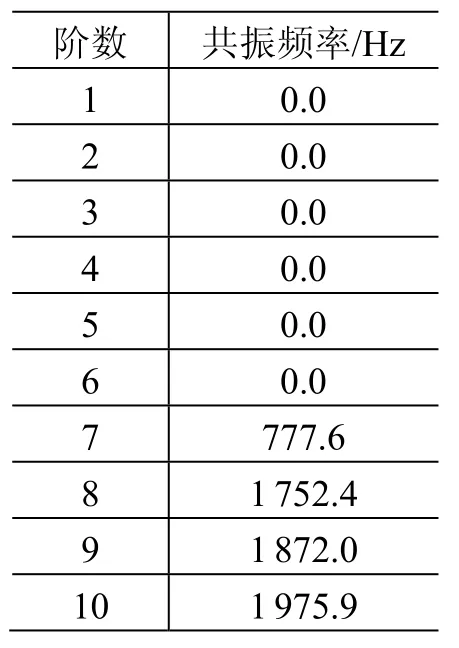
表1 工作平台共振频率Table 1 The resonant frequencies of the platform

2 试验验证

2.1 三轴振动试验

本试验的工作平台连接3套5 t电动振动台（见图6），联调时使用多维控制仪对各个振动台及平台空载状态进行正弦扫频试验，以获得系统的动态性能指标（主要是共振频率）。图7给出了传感器安装位置，1#加速度传感器位于平台几何中心，9#传感器位于对角线上，10#传感器位于中心线外边缘端。

2.2 试验结果分析

正弦扫频试验后，采用多输出控制仪内嵌的数据分析软件可计算得到各个通道上传感器响应与驱动信号的比值。图8、图9分别给出了 9#与10#传感器的响应与驱动信号的比值，可以看出，虽然传感器位于台面不同位置处，对于同一频率响应幅值不尽相同，但是 9#与 10#传感器分别在720 Hz与1 872.5 Hz处都有较大的波峰，结合工程实施经验，这2个频率为工作台面的共振频率。

将数值模拟所得的模态频率与试验测试所得台面的固有频率进行对比，结果见表2。可以看出，试验测得工作平台第1阶固有频率为720 Hz，而模态分析得到的固有频率为777.6 Hz，相差57.6 Hz，相对偏差为7.4%，振型为对角弯曲；同理，试验测得工作平台第2阶固有频率为1 872.5 Hz，模态分析固有频率为1 752.4 Hz，相差120.1 Hz，相对偏差为6.4%，振型为对边弯曲。分析偏差的原因，是因为仿真计算频率采用自由模态方法，而试验测量频率是在有约束条件的振动环境下测得的。

表2 共振频率数据对比Table 2 Resonance frequency comparison of analysis and test results

3 结论

本文对三轴振动试验系统的工作平台进行了有限元建模和模态分析，又对该结构进行三轴振动试验验证，得到以下结论：

1）对工作台面进行有限元仿真自由模态分析，能够得到台面的对角和对边的弯曲频率，进而预测系统的工作频率范围，并验证系统设计的合理性和有效性；

2）工作台面在模态分析过程中，台面的螺纹孔、倒角和圆角对模态频率影响很小，仿真计算过程中可以不予考虑；

3）工作平台除平动频率外，第1阶为对角弯曲频率，第2阶为对边弯曲频率，其余各阶均为对称振型或边角局部振型，对测试结果无明显影响。

研究结果表明，三轴振动试验系统工作平台的仿真计算对系统关键动态参数有很好的预测作用，能够指导系统的设计。

（References）

[1]PITOISET X, PREUMONT A.Tools for a multiaxial fatigue analysis of structures submitted to random vibrations[J].Journal of Vibration and Acoustics, 1994, 45(3): 289-294

[2]NIESŁONY A.Comparison of some selected multiaxial fatigue failure criteria dedicated for spectral method[J].Journal of Theoretical and Applied Mechanics, 2010, 48(1): 233-254

[3]张正平, 邱吉宝, 王建民, 等.航天器结构虚拟动态技术新进展[J].振动工程学报, 2008, 21(3): 209-221 ZHANG Z P, QIU J B, WANG J M, et al.Progress on virtual dynamic test techniques for space vehicles[J].Journal of Vibration Engineering, 2008, 21(3): 209-221

[4]周兴广.多轴随机振动环境的疲劳损伤机理浅析[J].航天器环境工程, 2010, 27(6): 723-726 ZHOU X G.Brief analysis of fatigue failure methods under multiaxial random vibration environment[J].Spacecraft Environment Engineering, 2010, 27(6): 723-726

[5]邱汉平, 冯咬齐, 樊世超.多轴随机振动试验控制技术研究[J].航天器环境工程, 2015, 32(5): 527-531 QIU H P, FENG Y Q, FAN S C.The multi-axis random vibration test control techniques[J].Spacecraft EnvironmentEngineering, 2015, 32(5): 527-531

[6]苏嵩, 陈红光, 郁林聪.高频电液振动台用台面的性能分析及优化设计[J].液压与气动, 2009(2): 19-21 SU S, CHEN H G, YU L C.Design optimization and analysis of head expander for high-frequency electrohydraulic vibration generator[J].Chinese Hydraulics & Pneumatics, 2009(2): 19-21

[7]王东升, 刘青林, 张志旭.多轴振动台台面频率优化[J].航天器环境工程, 2008, 25(4): 351-354 WANG D S, LIU Q L, ZHANG Z X.The frequency-optimization of the multi-axes vibration generator’s table-board[J].Spacecraft Environment Engineering, 2008, 25(4): 351-354

[8]黄舟, 黄海.六自由度振动台台体结构优化设计研究[J].航天器环境工程, 2015, 32(5): 560-565 HUANG Z, HUANG H.Structure optimization design of 6-DOF shaker’s table[J].Spacecraft Environment Engineering, 2015, 32(5): 560-565

（编辑：许京媛）

Resonant frequency analysis on the platform of tri-axial vibration system

ZHOU Xingguang, TIAN Zhenqiang, WANG Bing, QIN Yaming, HE Zhiguo
(Beijing Institute of Structure and Environment Engineering, Beijing 100076, China)

To verify and increase the resonant frequency of the platform of a tri-axial vibration test system, and furthermore, to extend the frequency range of the system, the mode of the work table under the free state is simulated using the FEM software, and the simulation results and the tri-axial test results are compared.It is shown that the differences of the bending frequency of the opposite angles or sides are less than 10%.And the result can provide a technical support for the future design.

tri-axial vibration test system; platform; dynamic characteristics; resonant frequency; simulation analysis

V416.8; TB115

：A

： 1673-1379(2017)01-0035-05

10.3969/j.issn.1673-1379.2017.01.006

周兴广 (1980—)，男，硕士学位，高级工程师，研究方向为强度、振动与可靠性。E-mail: zhouxg2008@126.com。

2016-08-15；

：2017-01-17

中国航天科技集团公司科技创新研发项目“大推力多轴电动振动系统关键技术研究”

周兴广，田振强，王冰，等.三轴振动试验系统工作平台的谐振频率分析[J].航天器环境工程, 2017, 34(1): 35-39

ZHOU X G, TIAN Z Q, WANG B, et al.Resonant frequency analysis on the platform of tri-axial vibration system[J].Spacecraft Environment Engineering, 2017, 34(1): 35-39