基于遗传规划算法的不同应力比下不同厚度7050铝合金疲劳裂纹扩展寿命预测
罗豪鑫,陈传勇,刘建中,张丽娜
(1.浙江大学,浙江 杭州 310027; 2.北京航空材料研究院,北京 100095)
基于遗传规划算法的不同应力比下不同厚度7050铝合金疲劳裂纹扩展寿命预测
罗豪鑫1,陈传勇1,刘建中2,张丽娜2
(1.浙江大学,浙江 杭州 310027; 2.北京航空材料研究院,北京 100095)
针对不同厚度7050铝合金试样进行了不同应力比条件下的一系列疲劳裂纹扩展试验,并运用遗传规划算法对疲劳裂纹扩展寿命进行预测。遗传规划算法是模拟自然界中生物的进化策略,通过交换、突变等遗传操作,搜索目标的最优解。建立7050铝合金疲劳裂纹扩展速率的遗传规划模型,并利用试验数据对模型进行测试,后与其他典型疲劳裂纹扩展模型进行比较。研究结果表明:GP模型预测的7050铝合金疲劳裂纹扩展寿命结果与试验值基本吻合,相对误差小于1.5%,且GP模型预测结果的准确性高于Paris模型和Walker模型。
遗传规划算法模型; 疲劳裂纹扩展寿命; 疲劳裂纹扩展速率; 应力比; 厚度
1 引 言
近年来,世界铝工业和铝材料加工技术飞速发展,尤其在航天航空领域显得格外突出,这使得铝合金越来越成为人们关注的对象。其中7050铝合金的用量最大,应用范围最广,是铝合金中的王牌合金。7050铝合金是Al-Zn-Mg-Cu系高强度合金,在较高强度水平下具有韧性好、疲劳强度高、抗腐蚀能力强等优良的综合性能,是一种新型的、很有应用前景的结构材料。
但是,任何受载材料在制造过程中都会含有一些小的缺陷。在交变载荷作用下,这些缺陷将导致裂纹的产生,然后裂纹逐渐扩展到危险临界尺寸,并最终导致毁灭性的失效。近年来,由于疲劳裂纹而导致破坏事故的例子在航海航空、土木工程等国民经济的重要领域中屡见不鲜。
因此,有必要对材料的疲劳裂纹扩展问题进行研究,为选择合适的检测周期提供一定的指导方针,同时也为结构疲劳剩余寿命评估以及疲劳损伤监测提供重要依据。邓斌等人分析了不同腐蚀环境对铝合金疲劳性能的影响[1],宋千光等人研究了温度和应力比对航空铝合金疲劳裂纹扩展规律的影响[2]。但从现有文献看,针对不同厚度铝合金不同应力比下的疲劳裂纹扩展试验数据和寿命预测的研究还很少,试样厚度的变化会导致其所处状态由平面应力趋向平面应变,从而影响疲劳裂纹扩展速率[3]。本文针对不同厚度中心开裂7050铝合金板,开展不同应力比下的疲劳裂纹扩展试验,进而预测疲劳裂纹扩展寿命,为7050铝合金的工程应用提供技术保证。
2 遗传规划算法背景介绍
九十年代初美国学者Koza在遗传算法的基础上提出了一种全新的结构描述方法——遗传规划算法。遗传规划算法是模拟生物在自然环境中的遗传和进化过程而形成的一种自适应全局优化概率搜索算法。它与进化算法的主要不同表现在以动态的树结构来表示染色体。遗传规划算法具有描述问题层次化、编码长度动态可变等特点,被广泛地应用于人工智能、符号处理等方面[4-7]。
这里的求和仅仅理解为多边矩阵的剖面的另一种记号,因为作为矩阵,它们是无法求和的,因为各项的矩阵阶数是不同的。如果记一个二元函数π(x,y)满足当x和y都是数值时,π(x,y)=xy,而当x是数值,y是向量(y1,y2)T时,π(x,y)=xy1+xy2,那么利用该运算符号π(x,y)作为矩阵A和B的广义交叉乘法的数据层面的运算,而框架层面的运算仍然采用普通矩阵乘法的运算法则,可以定义矩阵A和B的广义交叉乘法如下:
利用遗传规划算法建立GP模型可直接得到7050铝合金疲劳裂纹扩展速率da/dN与应力比R,厚度t,应力强度因子ΔK的数学关系式,即可用唯一的数学式描述不同应力比下不同厚度7050铝合金疲劳裂纹扩展速率。而其他典型疲劳裂纹扩展模型[8],如Paris模型与Walker模型,其表达式分别为:
3.3.4 把握秸秆禁烧政策以“疏”为主的重心 现行状况下,秸秆禁烧政策存在单一高压的特点,导致政策发挥效果片面化,在高压的禁烧政策下也不能真正解决秸秆焚烧的问题。落实秸秆禁烧的政策,首先考虑信阳本地情况,兼顾政策的合法性与合理性,制定符合该地区发展的多元化、科学化和人性化政策。在政策奖罚制定过程中,要注重秸秆的综合利用,尽量从“疏”的角度出发,指导秸秆禁烧政策的落实。
(1)
(2)
前者只能描述与预测某一厚度试样在某一特定应力比下疲劳裂纹扩展速率,但其预测值准确性较高;后者能够描述与预测某一厚度试样各应力比下疲劳裂纹扩展速率,但其预测值准确性不高。因此Paris模型与Walker模型各有局限性[9-14]。
遗传规划算法在模型预测方面得到了较普遍的应用,且在处理复杂非线性问题时具有十分明显的优势。例如在3C钢腐蚀性能预测分析[15]及NdFeB永磁体性能预测[16]中,应用类似数据库算法建立的模型都显示出了强大的指导作用。因此,本文利用遗传规划算法的思想来预测7050铝合金疲劳裂纹扩展速率与寿命的问题。
3 试验过程
3.1 材料及试样
对裂纹长度进行实时观测的同时,使用VMM2.2C图像处理软件按照一定循环间隔对裂纹图像进行拍摄,拍摄间隔最初设置为5000个载荷循环,而后随着裂纹扩展速率的不断增加,拍摄间隔按照4000、3000、2000、1000、500、300、200的顺序逐次递减,保证每相邻两次拍摄间隔中裂纹扩展长度不超过0.5mm。试验后采用GB/T 6398-2000推荐的递增多项式法对裂纹扩展速率进行处理,将裂纹扩展速率da/dN表示为应力强度因子ΔK的函数式。7050铝合金M(T)试样应力强度因子ΔK定义为:
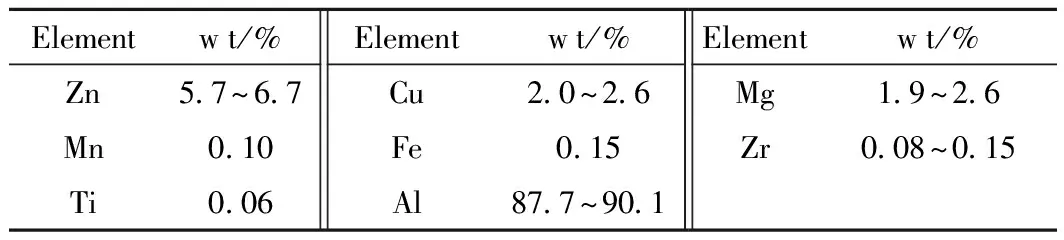
表1 7050铝合金的化学成分

表2 7050铝合金的力学性能
试验试样按照GB/T 6398-2000《金属材料疲劳裂纹扩展速率试验方案法》和E647-08《Standard Test Method for Measurement of Fatigue Crack Growth Rates》进行设计,其形状为标准矩形板状,长为300mm,宽为75mm,厚度为3和7mm,初始裂纹长度a0为2.5mm,如图1所示。
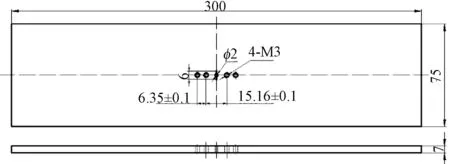
图1 7050铝合金疲劳裂纹扩展试样Fig.1 Specimen of 7050 aluminum alloy for fatigue crack growth test
3.2 试验设备和方法
试验在常温空气环境下,MTS-810电液伺服疲劳试验机上进行,如图2所示。试验中采用应力幅控制方式进行裂纹扩展,裂纹长度测量采用柔度法结合光学观测方法。其中,柔度法使用系统自带的COD张开规,光学测量采用专门设计的高倍率读数显微系统。此系统由CCD读数显微镜和VMM2.2C图像处理软件构成,能够实时进行裂纹长度观测,分辨率达到0.01mm。

图2 疲劳裂纹扩展试验系统Fig.2 Fatigue crack growth test system
式中,(da/dN)ex是7050铝合金疲劳裂纹扩展结果试验值;(da/dN)pre是GP模型的预测值;(da/dN)’ex是7050铝合金疲劳裂纹扩展结果试验平均值;(da/dN)’pre是GP模型预测平均值;n是所选数据点的数目。
“其他同学的父母因为忙于工作不能到场,你们回去后也可以和父母说一声‘您辛苦了’,他们也会非常高兴的。”
疲劳裂纹扩展中循环加载波形为正弦波,频率为10Hz,基线载荷Smax=65MPa,取三级应力比分别为R=0.06、0.5和-1。为保证试验数据的准确性,每个应力比下至少做2个相同厚度的试样。
至此为止,课堂上,学生就像打开了潘多拉魔盒一样兴奋起来,“我发现:3格的一半是1格半,再加上半格也是2格!(如图6)”“5格的一半是2格半,去掉半格也是2格!(如图7)”甚至有学生提出:要是钉子板再长些,这样也可以,这是8格的一半4格,去掉4格的一半是2格(如图8)……
本次试验研究的材料为7050铝合金,材料的化学成分和力学性能如表1和表2所示。
(3)
● 误食尖锐的物品:如钉子、碎玻璃等。不可给予任何液体及催吐,紧急就医。因为尖锐的物品可能会划伤食道和气管。
4 构建GP模型
5.2 GP模型与Paris模型、Walker模型的比较
式中,ΔS是应力变化量;a是裂纹长度;W是试样宽度。
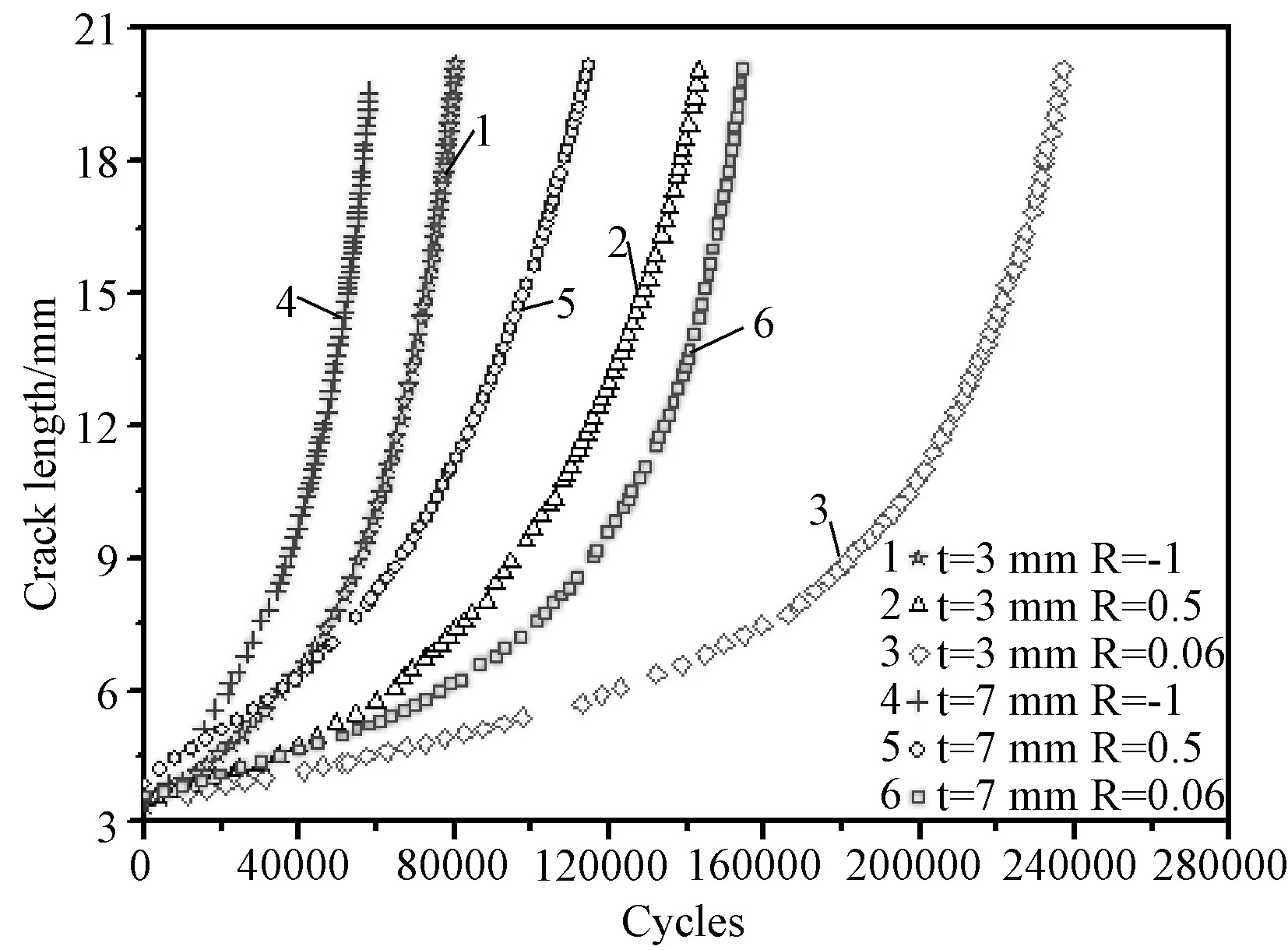
图3 不同厚度7050铝合金在不同应力比下的a-N曲线比较Fig.3 Comparison of a-N curves of 7050 aluminum alloy with different thicknesses under various load ratios
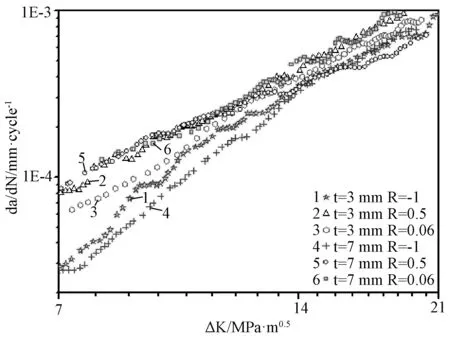
图4 不同厚度7050铝合金在不同应力比下的da/dN-ΔK曲线比较Fig.4 Comparison of da/dN-ΔK curves of 7050 aluminum alloy with different thicknesses under various load ratios
建立GP模型时,各应力比下不同厚度的7050铝合金疲劳裂纹扩展试验数据均有三个输入变量R、t、ΔK,一个输出变量da/dN,取值范围如表3所示,其中每一组试验所测裂纹扩展速率点均在100个左右。
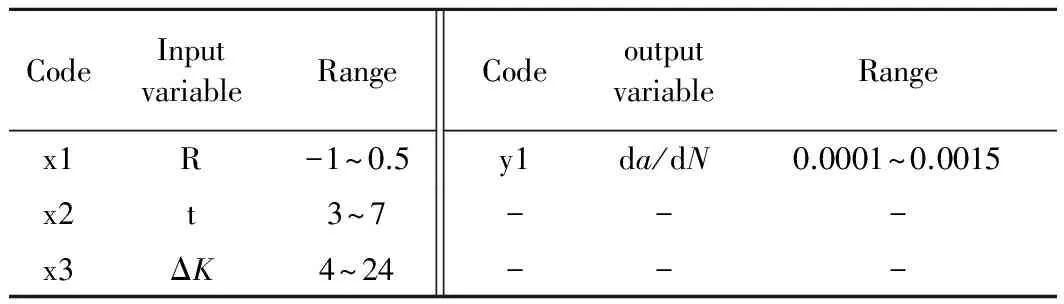
表3 建立GP模型所使用的变量
图5为GP模型拟合所得二叉树最终结构,此二叉树表明三个输入变量(R、t、ΔK)与输出变量da/dN之间的数学关系,而这种关联性可用于疲劳裂纹扩展过程的预测。

表4 GP模型所选参数
疲劳裂纹扩展前先采用应力控制方式预制裂纹,采用正弦波加载,频率为10Hz,应力比R=0.06,应力水平为Smax=65MPa。预制裂纹长度为1mm,故预制裂纹结束后进行裂纹扩展的初始裂纹长度为ai=3.5mm。
遗传规划算法一开始是由1000个随机生成的电脑程序(初始群体规模)组成的。这1000个电脑程序 不断发生遗传进化,同时伴随着一定概率的突变与交换。此过程中,电脑程序演变出的结果可以用来表示输入与输出变量之间的关系。根据遗传规划算法得到的疲劳裂纹扩展速率可以用一个直观的数学式表达:
模糊综合评价是多重目标决策的一种情形,主要用于模糊环境,通过对事物影响因素进行模糊关系方程匀速,针对一定的目的对事物做出综合评价. 模糊综合评判的过程包括综合考虑各种属性,建立被评判对象的因素集;建立评判集;进行单因素评判;为不同因素赋权值,根据权值和单因素评判结果得出综合评判结果[9].
1.3 观察指标 比较两组患儿治疗前、后的肺功能指标,包括肺活量(FVC)、第一秒呼出气体容积(FEV1)、 FEV1/FVC、免疫功能指标(CD4+、CD8+、CD4+/CD8+)、血清IgE水平、细胞因子水平(IFN-γ、IL-4)及治疗效果。临床治疗效果判定标准:显效:治疗1周患儿咳痰、气促、呼吸困难症状消失,肺部哮鸣音消失,3个月内无复发;有效:治疗1周患儿咳痰、气促、呼吸困难等症状明显减轻,肺部哮鸣音减轻,3个月内无复发;无效:治疗1周患儿咳痰、气促、呼吸困难等症状无明显好转,甚至加重,肺部哮鸣音无改变甚至恶化。治疗有效率=(显效+有效)例数/总例数×100%。
(4)
(5)
(6)
用试验数据对GP模型进行训练,优化每个个体的适应度,运行达到群体的最大数目为7000停止,此时,程序会给出疲劳裂纹扩展速率最佳拟合公式,即GP模型的最终结果。本试验中,7050铝合金在各参数限制条件下由遗传规划算法得到的疲劳裂纹扩展速率最佳拟合公式为:
0.000002ΔK2-0.000065
(7)
选择不同的限制参数,如初始群体规模、群体数目、函数集、突变概率和交换概率等来获得能够描述7050铝合金疲劳裂纹扩展速率的最佳GP模型[17-20]。GP模型中参数的取值及函数集类型的选择均取决于所需解决问题的具体性质,并采用相关系数R和均方差MSE衡量以上参数适应性。反复测试后可得参数选择如表4所示时,拟合的GP模型效果最佳,即相关系数R较高,均方差MSE较小。

图5 7050铝合金裂纹扩展速率二叉树最终结构Fig.5 Final tree structure of 7050 aluminum alloy crack growth rate
5.1 GP模型预测结果
GP模型预测所得7050铝合金疲劳裂纹扩展结果与试验值相比,相关系数R为0.9486,均方差MSE为10-6,两者基本吻合,即用GP模型预测7050铝合金疲劳裂纹扩展结果是可行的。GP模型拟合公式为裂纹扩展速率da/dN,应力比R,试样厚度t与应力强度因子幅值ΔK之间的数学关系,而疲劳裂纹扩展寿命即载荷循环数N可采用切线法对上述拟合公式累加得到:
(8)
式中,Ni+1是第i+1次的载荷循环数;Ni是第i次的载荷循环数;ai+1是载荷循环数Ni+1时的裂纹长度;ai是载荷循环数Ni时的裂纹长度;(da/dN)GP是GP模型预测所得疲劳裂纹扩展速率。
恒幅载荷下不同厚度(t=3,7mm)7050铝合金在不同应力比(R=0.06,0.5,-1)下所有a-N和da/dN~ΔK的试验数据点如图3和图4所示。GP遗传规划算法将对试验中各工况下疲劳裂纹扩展速率da/dN与应力比R,厚度t和应力强度因子ΔK进行定量的数学描述,并对其裂纹扩展寿命进行预测。
限于篇幅,本文以厚度t=3mm,应力比R=0.06时7050铝合金疲劳裂纹扩展结果为例,对7050铝合金疲劳裂纹扩展速率、裂纹长度的试验值与Paris模型、Walker模型和GP模型的预测值进行比较。图6、图7分别表示a-N和da/dN-ΔK曲线的对比图,图中四条曲线分别为试验值、Paris模型、Walker模型和GP模型的预测值。
(1)二维超声表明胎盘间隙已经消失,且胎盘下肌菲薄。(2)经过彩色多普勒超声检查后,表明胎盘后方或胎盘实质血流异常丰富,能够对动脉血流进行准确探测,具体表现为:胎盘实质血流紊乱等,甚至牵连子宫肌层。

图6 Paris模型,Walker模型,GP模型和试验所得a-N曲线的比较Fig.6 Comparison of a-N curves of Paris model, Walker model, GP model and experiment

图7 Paris模型,Walker模型,GP模型和试验所得da/dN-ΔK曲线的比较Fig.7 Comparison of da/dN-ΔK curves of Paris model, Walker model, GP model and experiment
由图6、图7中可见,在疲劳裂纹扩展初级阶段,载荷循环数较少,裂纹长度较短,应力强度因子ΔK较低,Paris模型,Walker模型,GP模型的预测值与试验所得a-N和da/dN-ΔK曲线的重合度较高,四条曲线基本完全重合,这表明在疲劳裂纹扩展初级阶段三种模型均能较为准确地描述与预测疲劳裂纹扩展速率和寿命;随着裂纹的扩展,应力强度因子ΔK逐渐增大,Paris模型对于疲劳裂纹扩展速率与寿命的预测值与试验值相对误差越来越大,Walker模型的预测值与试验值相对误差先减小后增大,且随着循环数N的增加,相对误差越来越大,而GP模型的预测值不断逼近试验值,相对误差不断减小,其精度越来越高。
带式过滤机主要由橡胶带、真空盒、进料装置、滤饼洗涤装置、滤布纠偏装置、滤布张紧装置、橡胶带驱动辊轮与张紧装置、滤布及橡胶带清洗、卸料装置及电控柜等组成[2]。通过PLC控制系统对进料、压滤、滤布冲洗、卸料等操作值的设定,经通信电缆将现场的实时数据传送至仪表室,可实现DCS远程控制。
表5列出了Paris模型、Walker模型和GP模型对于疲劳裂纹扩展速率预测值与试验值的比较结果。Pairs模型预测值的相关系数R最高为0.9824,但均
方差MSE较大为6.517×10-9;Walker模型预测值的相关系数R最低为0.9407,均方差MSE最大为1.847×10-8;GP模型预测值的相关系数R较高为0.9736,均方差MSE最小为1.589×10-9。因此选择GP模型对7050铝合金疲劳裂纹扩展结果进行预测是准确且合理的。
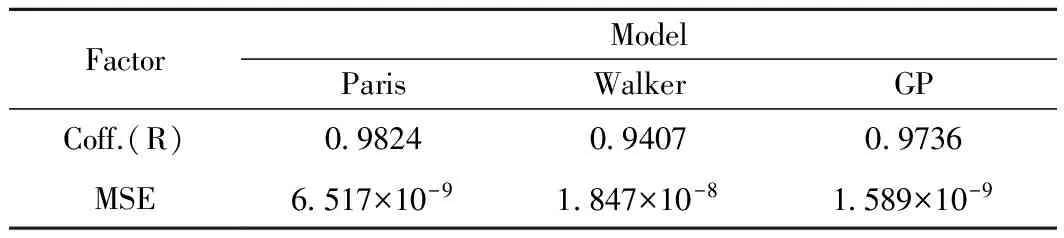
表5 Paris模型,Walker模型和GP模型所得da/dN~ΔK结果的比较
为进一步验证GP模型预测疲劳裂纹扩展寿命的准确性,表6给出了裂纹由相同初始长度ai=3.5mm扩展到相同终止长度af=20.5mm时,各模型寿命预测值的精度。Paris模型和Walker模型寿命预测值的相对误差分别达到4.29%和2.60%,GP模型的预测精度最高,相对误差仅为0.402%,相对比值为1.004,即GP模型的预测结果最为准确。
5.3 结果分析
世界六大马拉松大满贯赛事,基本都具有40年的历史(东京马拉松11年历史),其中最悠久的当属波士顿马拉松(简称波马),创立于1897年,120年的城市文化积淀成就了波马的马拉松文化。波士顿马拉松也是最具仪式感的赛事,赛前晚宴在波马博览会上进行,选手穿着波马纪念服观看波马宣传片、纪录片,浓浓的仪式感让即将参赛的选手热情高涨。仪式、建筑、民俗构成波士顿马拉松独特的文化属性,但最具赛事文化的是波马的极端恶劣天气、最难赛道、勇于挑战自我的波马选手共同构建出的“世界跑者殿堂”——波士顿马拉松,象征着更高的精神追求,这正是波马logo独角兽的内涵。
GP模型的适应性与精确性主要通过疲劳裂纹扩展寿命预测值与试验值的相对误差、相对比和误差带来衡量。其中,表6已对相对误差和相对比做了分析描述。
6-12月龄TUBABC品系野生型斑马鱼成鱼,饲养于苏州大学生物钟研究中心。采用专业的饲养系统(上海海圣工贸有限公司)进行饲养,水温维持在28.5±1℃,pH为 7.2-7.6之间,鱼房的光照周期为 14小时光照/10小时黑暗,即14L:10D,每天早晚喂食丰年虾,中午喂食干饲料。
图8给出了GP模型疲劳裂纹扩展寿命预测值的误差带。由图8中可见,当疲劳裂纹扩展寿命即载荷循环数N较大时,GP模型的预测值均在±1% 的误差带区域内,且随着循环数N的增大,误差值不断减小,越接近于试验所得寿命。与GP模型相比,Paris模型与Walker模型预测值的误差较大,均超过±1%,且随着循环数N的增大,误差值并无明显减小。这表明用GP模型预测7050铝合金疲劳裂纹扩展寿命是可行的,且载荷循环数越接近真实寿命时,预测值越精确。

表6 Paris模型,Walker模型,GP模型的寿命预测值与试验值的比较
*Nexperimental是7050铝合金裂纹扩展寿命试验值;Npredicted是各模型对7050铝合金裂纹扩展寿命的预测值。

图8 预测寿命值的误差带Fig.8 Error band scatter of predicted lives
采用遗传规划算法得到的GP模型所预测7050铝合金疲劳裂纹扩展的结果与试验结果基本吻合,相对误差在1.5%以内,相关系数为0.9486,均方差为10-6,其值均在工程允许范围之内。运行结果以二叉树的形式表达出来,更为直观地确定了影响7050铝合金疲劳裂纹扩展的主要因素(应力比R、厚度t和应力强度因子ΔK)与寿命和扩展速率之间的非线性关系,并通过比较验证了GP模型的预测结果准确性优于Paris模型和Walker模型。这表明用遗传规划算法预测疲劳裂纹扩展寿命有很好的效果,为疲劳裂纹扩展寿命的预测开辟了一条新的路径。
[1] 邓斌, 易丹青, 杨胜, 王斌. 2E12铝合金加速腐蚀环境下的疲劳裂纹扩展[J]. 材料科学与工程学报, 2009, 27(5): 770~773.
[2] 宋千光, 赵斌, 耿小亮, 邓俊艳, 刘畅. 温度和应力比对航空铝合金疲劳裂纹扩展规律的影响及其机理[J]. 材料科学与工程学报, 2015, 33(2): 157~162.
[3] Peishi Yu, Wanlin Guo. An equivalent thickness conception for prediction of surface fatigue crack growth life and shape evolution[J]. Engineering Fracture Mechanics, 2012(93): 65~74.
[4] 周永权. 泛函网络理论及其学习算法研究[D]. 西安电子科技大学, 2006.
[5] 郝艳伟. 遗传规划算法研究及其在仿人智能控制器结构自动设计中的应用[D]. 重庆理工大学, 2011.
[6] 云庆夏, 王占权, 黄光球. 遗传算法和遗传规划[M]. 北京:冶金工业出版社, 1997.
[7] 李敏强, 寇纪淞, 林丹. 遗传算法的基本理论与应用[M].北京: 科学出版社, 2002.
[8] S. M. Ben, S. Abdullah, A. K. Ariffin. Review of Fatigue Crack Propagation Models For Metallic Components[J]. European Journal of Scientific Research, 2009, 28(3): 364~397.
[9] D. Kujawski. A fatigue crack driving force parameter with load ratio effects[J]. International Journal of Fatigue, 2001(23): 239~246.
[10] D. Kujawski. Enhanced model of partial crack closure for correlation of R-ratio effects in aluminum alloys[J]. International Journal of Fatigue, 2001(23): 95~102.
[11] X. huang, T. Moan. Improved modeling of the effect of R-ratio on crack growth rate[J]. International Journal of Fatigue, 2007(29): 591~602.
[12] S. B. Singh, R. Kumar. Experimental observations of fatigue crack growth in IS1020 steel under constant amplitude loading[J]. Int. J. Press. Vessels Pip, 1993(53): 217~227.
[13] R. Kumar. Investigation of fatigue crack growth under constant amplitude loading[J]. Int. J. Press. Vessels Pip, 1990(41): 179~192.
[14] J. R. Monhanty, H. C. Das, A. C. Monhanty. A comparative study of fatigue life prediction of 7020 Al-alloy under load ratio effect[J]. Indian Journal of Engineering and Materials Sciences, 2014(21): 179~188.
[15] 刘艳侠, 高新琛, 张国英, 等. BP神经网络对3C钢腐蚀性能的预测分析[J]. 材料科学与工程学报, 2008, 26(1): 94~97.
[16] 储林华, 查五生, 刘锦云, 陈德波. 基于改进的BP神经网络的粘结NdFeB永磁体制备工艺优化研究[J]. 材料科学与工程学报, 2008, 26(6): 958~962.
[17] J.R. Koza. Genetic Programming: On the Programming of Computer by Means of Nature Selection[M]. Cambridge: the MIT Press, 1992.
[18] J.R. Koza. Genetic ProgrammingII: Automatic Discovery of Reusable Programs[M]. Cambridge: the MIT Press, 1992.
[19] Silva S, Costa E. Dynamic limits for bloat control: Variations on size and depth[C]. Deb K. Proceedings of GECCO, 2004, 666~667.
[20] Silva S, Silva P J N, Costa E. Resource-limited genetic programming: Replacing tree depth limits[C]. Ribeiro B. Proceedings of ICANNGA, 2005, 243~246.
Prediction of Fatigue Crack Growth Life of 7050 Aluminum Alloy with Different Thicknesses under Various Load Ratios by Genetic Programming
LUO Haoxin1, CHEN Chuanyong1, LIU Jianzhong2, ZHANG Lina2
(1.Zhejiang University, Hangzhou 310027, China; 2.Beijing Institute of Aeronautical Material, Beijing 100095, China)
In order to predict the fatigue crack growth life by genetic programming, fatigue test of 7050 aluminum alloy specimens with different thicknesses under various load ratios were carried out. Genetic programming simulates natural evolution by gene operations like crossover and mutation to get an optimal solution. The model of the fatigue crack growth of 7050 aluminum alloy was established by genetic programming and tested with the experimental data, also compared with other typical models. The results show that the model established by genetic programming matches with the experimental data, that relative error is less than 1.5%, with a higher accuracy than Paris model and Walker model.
Genetic Programming; fatigue crack growth life; fatigue crack growth rate; load ratio; thickness
1673-2812(2017)01-0026-06
2015-10-16;
2016-01-06
“863”课题资助项目(2012AA040104)
罗豪鑫(1991-),男,硕士研究生,研究方向:疲劳与断裂力学。E-mail:765738316@qq.com。
TG146.2; O346.2
A
10.14136/j.cnki.issn 1673-2812.2017.01.006

