考虑土拱效应的倾斜刚性挡墙非极限主动土压力

周亦涛，王学民，江文放，蔡燕燕

(1. 福州大学 土木工程学院，福建 福州 350116；2. 河北水利电力学院 交通工程系，河北 沧州061001；3. 华侨大学 土木工程学院，福建 厦门 361021)

考虑土拱效应的倾斜刚性挡墙非极限主动土压力

周亦涛1, 2，王学民2，江文放3，蔡燕燕3

(1. 福州大学 土木工程学院，福建 福州 350116；2. 河北水利电力学院 交通工程系，河北 沧州061001；3. 华侨大学 土木工程学院，福建 厦门 361021)

引入非极限内摩擦角同侧向位移的非线性关系；根据非极限状态下的倾斜墙背与滑裂面上的应力关系，以及水平微分层单元的水平静力平衡方程，得到了非极限滑裂面倾角，进而得到平移模式下考虑土拱效应和位移影响的倾斜刚性挡墙非极限主动土压力计算式。研究表明：侧向位移比的增大使非极限滑裂面倾角增大，非极限主动土压力系数减小，非极限主动土压力减小；墙背倾角的增大使非极限滑裂面倾角减小，非极限主动土压力系数减小，非极限主动土压力增大；非极限主动土压力随着填土内摩擦角、墙土摩擦角的增大而减小；与已有方法比较，提出的非极限主动土压力理论值与试验值吻合得更好。

岩土工程；非极限滑裂面倾角；土拱效应；非极限主动土压力；侧向位移比；墙背倾角

0 引 言

土压力大小和分布是挡土墙设计中至关重要的问题，其计算方法的合理性对挡土墙的安全和经济性影响巨大。用传统的朗肯和库仑土压力理论[1]计算土压力存在以下两个问题：①该理论未考虑土拱效应，得到的土压力均沿墙高呈线性分布，与试验结果所体现的非线性分布不符[2-3]；②该理论基于极限平衡状态下的土体进行分析，不适用于挡土墙墙背土压力计算，因为实际工程中的挡土墙并没有达到极限状态。

针对这两个问题，前人做了大量研究工作。R. L.HANDY[4]认为土拱效应可以用近似悬链线的小主应力轨迹来描述；K.H.PAIK等[5]假定小主应力拱形状为圆弧，对挡土墙后土拱效应进行了分析；蒋波[6]通过对比发现两种拱形下的土压力分布十分接近，建议选用圆弧形土拱。以上研究均基于极限平衡状态，未能进行非极限状态土压力的计算。S. BANG[7]将墙后土体的主动状态分为“初始、中间、完全主动状态”三个阶段；梅国雄等[8]，卢国胜[9]通过原位测试数据拟合该变化关系曲线，提出了考虑位移的土压力计算方法；卢坤林等[10]由卸荷应力路径试验，建立了填土内摩擦角与墙体位移的关系；卢坤林等[11]分析墙后小主应力拱的应力，得到平移模式下墙背垂直的非极限主动土压力计算式；张永兴等[12]，胡俊强等[13]认为挡土墙土压力是由墙后填土在平衡状态下出现的滑动楔体所产生；徐日庆等[14]从黏性土的应力莫尔圆出发，得到了黏性土的内摩擦角随墙体位移变化的关系公式；陈奕柏等[15]针对墙背倾斜、黏性填土表面倾斜的挡土墙进行分析，得到其非极限主动土压力公式。以上针对非极限土压力的研究中，仅有文献[11]考虑了土拱效应，但其采用的非极限库仑滑裂面倾角下的水平微分体的水平力平衡不满足，且仅针对墙背垂直的情况。章瑞文等[16]在对极限状态下的墙背土压力分析中，针对库仑滑裂面下水平微分层的水平静力平衡无法满足的情况，根据土拱效应和水平微分层的水平静力平衡得到了滑裂面倾角。

笔者针对现有非极限主动土压力研究的不足，

即非极限库仑滑裂面倾角下的水平微分体的水平力平衡不满足和没有考虑墙背倾斜的情况，在文献[16]的基础上，对平移模式下墙背倾斜的非极限主动土压力进行理论分析。根据土拱效应和水平层分析法得到非极限状态下的滑裂面倾角、主动土压力系数，进而得到主动土压力分布、土压力合力及其作用点的计算式。

1 非极限主动土压力分析

1.1 挡土墙模型分析

笔者的研究对象为墙背倾斜、填土为砂土的刚性挡土墙，如图1[15]。墙背倾角为ε，假设非极限状态下的墙后土体存在一个潜在的滑裂面倾角βm，挡土墙高H(m)，填土表面均布荷载q(kN/m)，填土容重为γ(kN/m3)，填土内摩擦角为φ，墙土摩擦角为δ。

图1 非极限挡土墙模型Fig.1 Model of non-limit retaining wall

1.2 非极限填土内摩擦角及墙土摩擦角

一般认为，非极限填土内摩擦角φm、非极限墙土摩擦角δm不会同时达到极限值[3]，为分析方便，假定二者同时达到极限值，并按式(1)、式(2)[13]计算：

(1)

(2)

式中：Rf为破坏比，取0.75～1.0；η为挡土墙非极限水平位移与极限水平位移之比；墙土摩擦角取δ=2φ/3[14]。

当η=1时，式(1)、式(2)计算的φm、δm分别为主动极限状态下的填土内摩擦角φ、墙土摩擦角δ；当η=0时，式(1)、式(2)计算的φm、δm分别为静止状态下的填土内摩擦角φ0、墙土摩擦角δ0[13]：

(3)

(4)

1.3 土体应力分析

由图2可以得到非极限状态下微元滑裂体在墙背处的法向应力σwm和切向应力τwm[17]：

(5)

τwm=σwmtanδm

(6)

式中：σ1m、σ3m为非极限状态下大、小主应力；Kam为非极限主动土压力系数，按式(7)计算：

(7)

由类似文献[17]的分析可得

(8)

式中：αwm为非极限微元滑裂体在墙面处的主应力偏转角。

同理，非极限状态下微元滑裂体在滑裂面处的法向应力σsm和切向应力τsm为

(9)

τsm=σsmtanφm

(10)

图2 滑裂体内土体非极限摩尔应力圆Fig.2 Mohr’s stress circle of non-limit sliding backfill

1.4 非极限滑裂面倾角

根据图1，由非极限微元滑裂体在水平方向的静力平衡可得

σwm-τwmtanε=σsm-τsmcotβm

(11)

将σwm，τwm，σsm，τsm代入式(11)，消去σ1m，得到非极限滑裂面倾角βm：

(12)

1.5 非极限主动土压力系数

由非极限微元滑裂体在竖直方向的静力平衡(图1)可得

(13)

由微元滑裂体在E点的力矩平衡可得

(14)

联立式(11)、式(13)及式(14)，可得倾斜墙背法向非极限主动土压力系数Kawm：

(15)

(16)

式中：Kwm为倾斜墙背非极限主动土压力系数。

1.6 非极限主动土压力

联立式(11)、式(14)，可得

(17)

其中：

(18)

式中破裂角βm按式(12)计算，解微分方程(17)，可得非极限微元滑裂体的平均竖向应力：

(19)

把式(19)代入式(15)，可得非极限墙背法向主动土压力：

(20)

(21)

对式(20)积分，可得非极限墙背法向主动土压力合力：

(22)

(23)

式中：Km为非极限总法向主动土压力系数。

对式(21)积分，得非极限墙背主动切应力合力：

(24)

由式(22)、式(24)可得非极限墙背主动土压力合力：

(25)

由式(20)得非极限墙背侧向土压力相对于墙趾的总弯矩：

(26)

由式(22)、式(26)，可得非极限墙背法向土压力合力的作用点相对墙基的高度：

(27)

2 结果分析与讨论

2.1 位移比、墙背倾角的影响

图3为ε、η对非极限滑裂面倾角、非极限主动土压力系数的影响曲线。由图3可见，非极限滑裂面倾角随着侧向位移比的增大而逐渐增大，随着墙背倾角的增大而逐渐减小；非极限主动土压力系数随着侧向位移、墙背倾角的增大而逐渐减小。

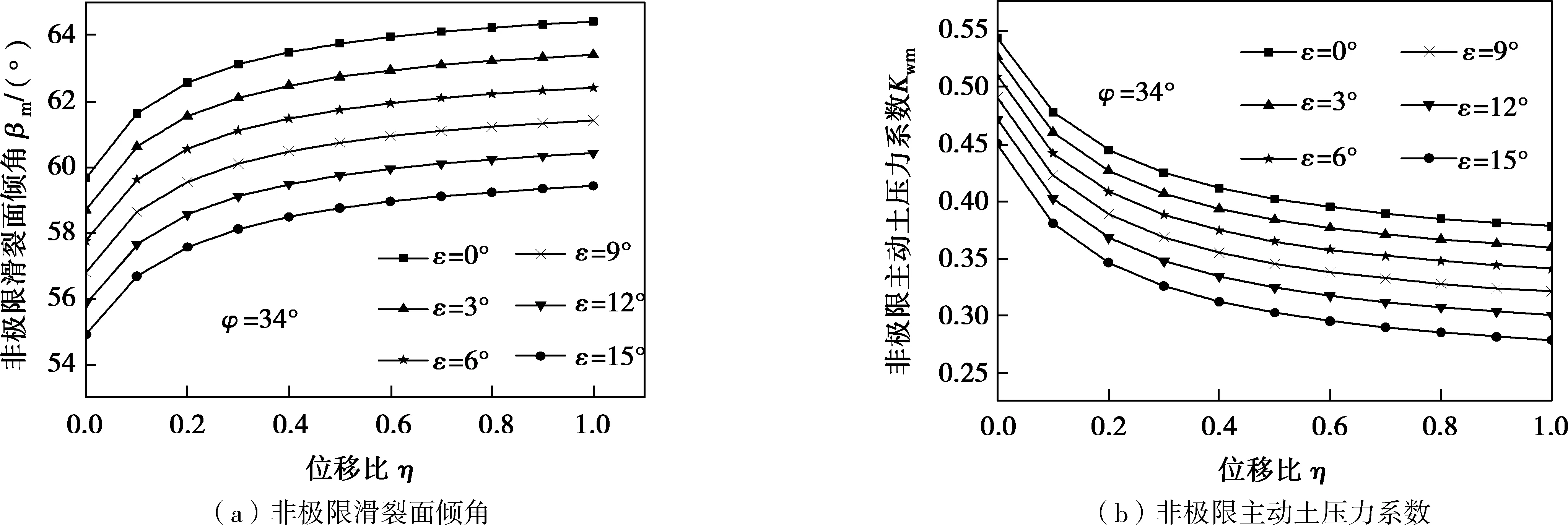
图3 非极限滑裂面倾角及非极限主动土压力系数随η、ε的变化Fig.3 Non-limit sliding surface inclination variation and non-limit active earth pressure coefficient variation with η and ε

图4为ε、η、y对非极限主动土压力的影响曲线。由4可见，非极限主动土压力随着侧向位移比的增大而减小，其减幅也随着侧向位移比的增大而

减小；非极限主动土压力在填土深度为[0, 0.33 m]时，随着墙背倾角的变化不大，而在填土深度为(0.33,1 m]时，随着墙背倾角的增大而逐渐增大。

图4 非极限主动土压力随η和ε的变化Fig.4 Non-limit active earth pressure variation with η and ε

2.2 填土内摩擦角、墙土摩擦角影响

图5，图6为填土内摩擦角φ，墙土摩擦角δ对非极限滑裂面倾角，非极限主动土压力系数及非极限主动土压力的影响线。由图5，图6可见：非极限滑裂面倾角随着墙土摩擦角的增大而增大，且增幅随着填土

内摩擦角的增大而减小；非极限主动土压力系数随填土内摩擦角的增大而减小，而随着墙土摩擦角在[0,φ]内增大；非极限主动土压力随填土内摩擦角的增大而减小；非极限土压力的极值随着墙土摩擦角的增大而有所减小，且位置沿着刚性挡墙向上移动。

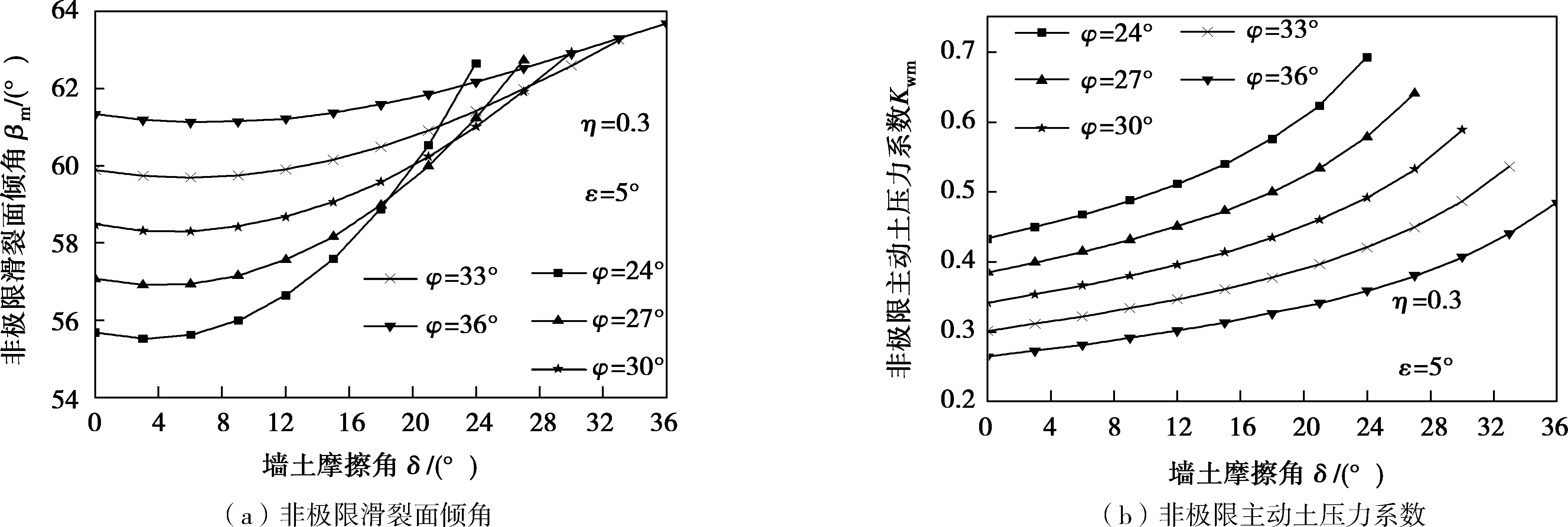
图5 非极限滑裂面倾角及非极限主动土压力系数随φ、δ的变化Fig.5 Non-limit sliding surface inclination variation and non-limit active earth pressure coefficient variation with φ and δ

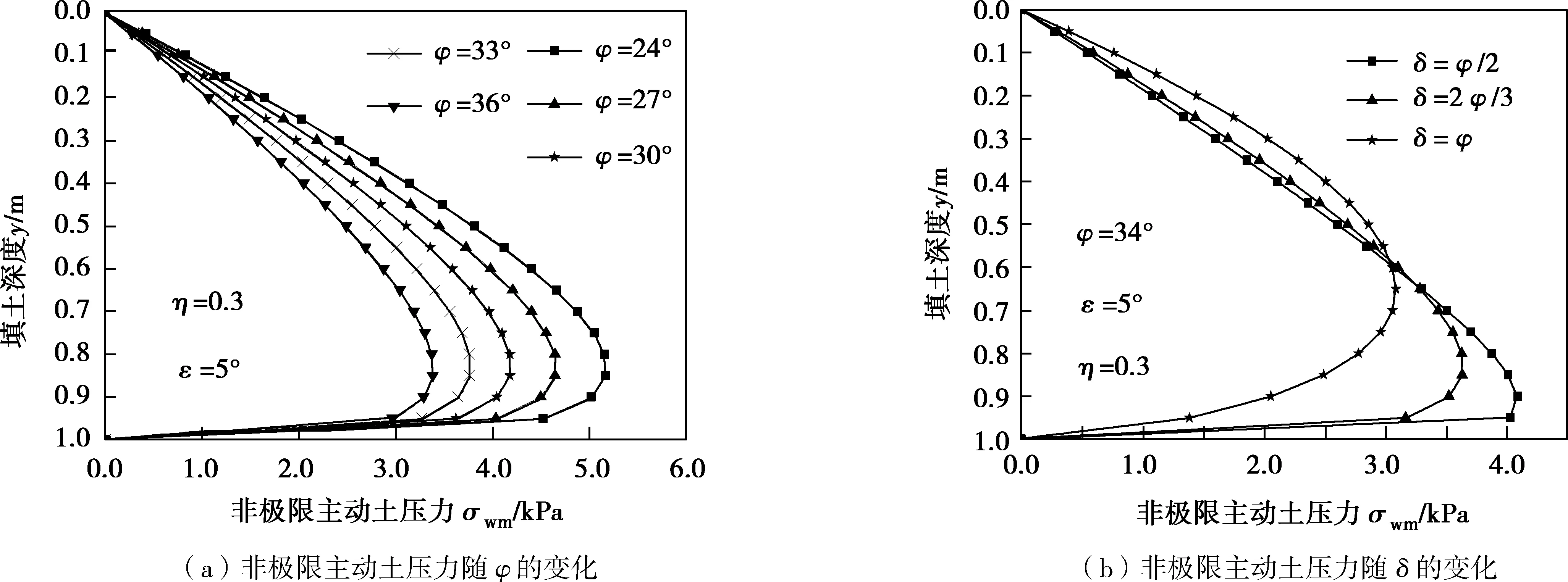
图6 非极限主动土压力随φ和δ的变化Fig.6 Non-limit active earth pressure variation with φ and δ

3 算例分析

图7给出了本文、卢坤林法[11]、胡俊强法[13]的非极限主动土压力计算结果和试验值[3]的对比。计算参数均同文献[3]：墙高H=1m，墙背倾角ε=0°，极限填土内摩擦角φ=34°，填土容重γ=15.4 kN/m3，极限墙土摩擦角δ=2φ/3，破坏比Rf=0.85，填土表面荷载q=0。

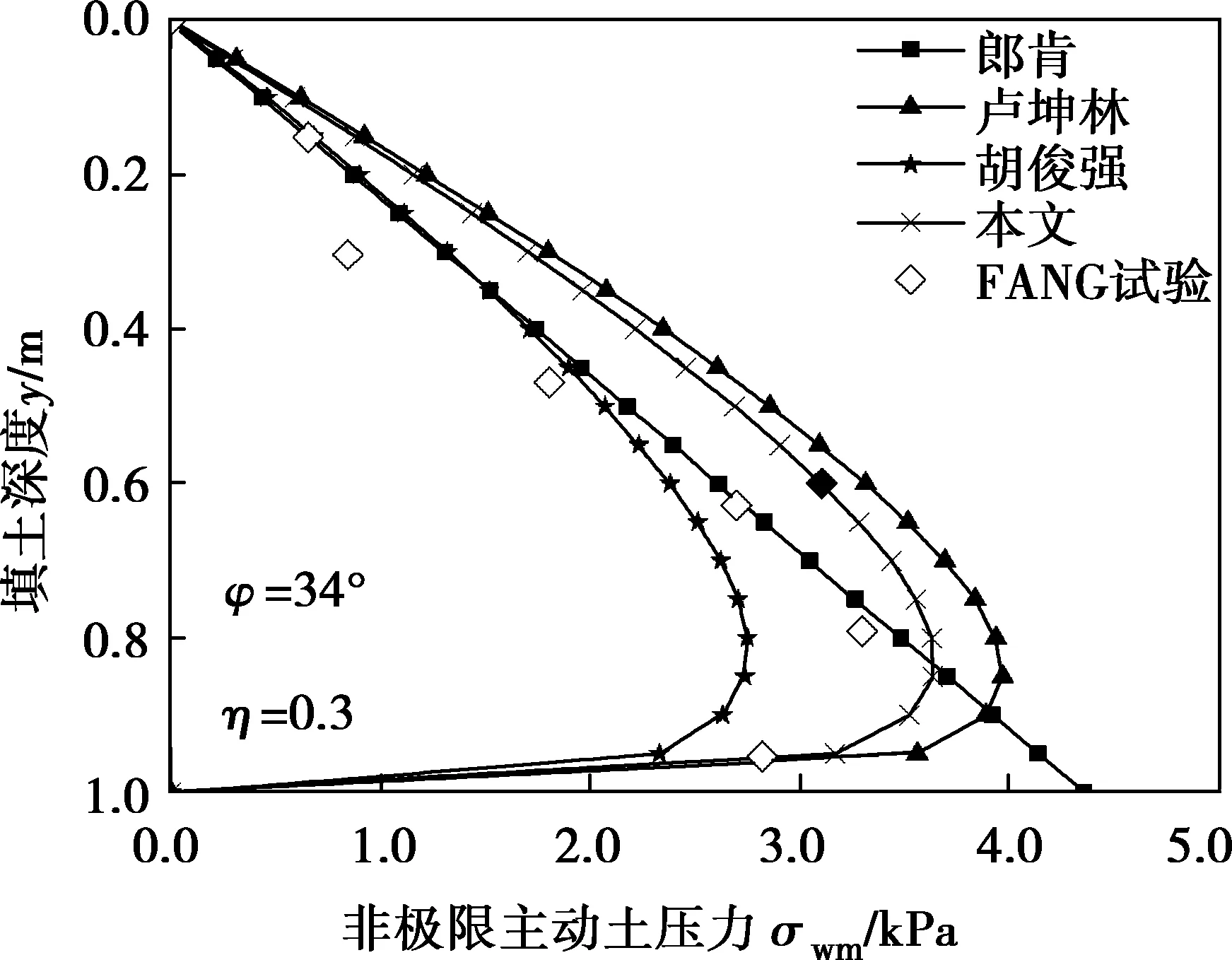
图7 不同方法的非极限主动土压力理论值与试验值的比较Fig.7 Comparison among non-limit active earth pressure bydifferent theoretical values and experimental values

由图7可知：相对于朗肯土压力沿墙高线性分布，笔者的非极限主动土压力理论值沿墙高呈现非线性分布，且极大值靠近墙趾；笔者的计算结果介于卢坤林[11]和胡俊强[13]的理论值之间，且与试验值吻合得更好。

图8为本文，胡俊强法，郎肯法的非极限主动土压力合力矩。

图8 不同方法的非极限主动土压力合力矩的比较Fig.8 Comparison among moment of non-limit active earthpressure by different theoretical values and experimental values

由图8可知：笔者方法及胡俊强法的合力矩值均大于朗肯法的合力矩，计算结果更加安全，且笔者的计算结果介于胡俊强和朗肯理论之间，经济效益较好；笔者方法和胡俊强法的合力矩值随着位移比的增大而逐渐减小；笔者方法和胡俊强法的合力矩值随着墙背倾角的增大而增大，且笔者方法的增幅较小。

4 结 论

1)笔者推导的非极限主动土压力理论值沿墙高呈现非线性分布，且极大值靠近墙趾，该计算方法的理论值介于卢坤林法和胡俊强法的理论值之间，且与试验值吻合得更好。

2)非极限主动土压力随着侧向位移比的增大而减小，其减幅也随着侧向位移比的增大而减小。非极限主动土压力在挡土墙的中下部，随着墙背倾角的增大而增大。

3)非极限主动土压力随填土内摩擦角、墙土摩擦角的增大而减小，非极限土压力极值随着墙土摩擦角的增大而减小。

[1] 顾慰慈.挡土墙土压力计算手册[M].北京：中国建材工业出版社，2005. GU Weici.ManualforEarthPressureAgainstRetainingWall[M].Beijing: China Building Materials Press, 2005.

[2] TSAGARELI Z V. Experimental investigation of the pressure of a loose medium on retaining walls with a vertical back face and horizontal backfill surface[J].SoilMechanicsandFoundationEngineering, 1965，2(4): 197-200.

[3] FANG Y S, ISHIBHISHI I. Static earth pressure with various wall movements[J].JournalofGeotechnicalEngineering, 1986,112(3): 313-333.

[4] HANDY R L. The arch in soil arching[J].JournalofGeotechnicalEngineering, 1985,111(3)：302-318.

[5] PAIK K H, SALGADO R. Estimation of active earth pressure against rigid retaining walls considering arching effects[J].Geotechnique, 2003,53(7): 643-653.

[6] 蒋波. 挡土结构土拱效应及土压力理论研究[D]. 杭州: 浙江大学, 2005. JIANG Bo.StudiesonSoilArchingEffectandEarthPressureforRetainingStructure[D].Hangzhou: Zhejiang University，2005.

[7] BANG S. Active earth pressure behind retaining walls[J].JournalofGeotechnicalEngineeringDivision, 1985, 111(3): 407-412.

[8] 梅国雄，宰金珉.考虑位移影响的土压力近似计算方法[J].岩土力学，2001，22(4)：83-85. MEI Guoxiong, ZAI Jinmin. Earth pressure calculating method considering displacement[J].RockandSoilMechanics，2001，22(4)：83-85.

[9] 卢国胜.考虑位移的土压力计算方法[J].岩土力学，2004，25(4)：586-589. LU Guosheng. A calculation method of earth pressure considering displacement[J].RockandSoilMechanics，2004，25(4)：586-589.

[10] 卢坤林，杨扬.非极限主动土压力计算方法初探[J].岩土力学, 2010, 31(2)：615-619. LU Kunlin, YANG Yang. Preliminary study of active earth pressure under non-limit state[J].RockandSoilMechanics，2010，31(2)：615-619.

[11] 卢坤林，朱大勇，杨扬.考虑土拱效应的非极限主动土压力计算方法[J].中国公路学报，2010，23(1)：19-25. LU Kunlin，ZHU Dayong，YANG Yang. Calculation method of active earth pressure under non-limit state considering soil arching effects[J].ChinaJournalofHighwayandTransport，2010，23(1)：19-25.

[12] 张永兴, 陈林. 挡土墙非极限状态主动土压力分布[J]. 土木工程学报, 2011, 44(4): 112-119. ZHANG Yongxing, CHEN Lin. Active earth pressure on retaining walls in non-limit state[J].ChinaCivilEngineeringJournal，2011，44(4)：112-119.

[13] 胡俊强, 张永兴, 陈林, 等. 非极限状态挡土墙主动土压力研究[J]. 岩土工程学报, 2013，35(2): 381-387. HU Junqiang，ZHANG Yongxing，CHEN Lin，et al. Active earth pressure on retaining wall under non-limit state [J].ChineseJournalofGeotechnicalEngineering，2013，35(2)：381-387.

[14] 徐日庆, 廖斌, 吴渐, 等. 黏性土的非极限主动土压力计算方法研究[J]. 岩土力学, 2013，34(1): 148-155. XU Riqing, LIAO Bin, WU Jian, et al. Computational method for active earth pressure of cohesive soil under non-limit state [J].RockandSoilMechanics，2013，34(1)：148-154.

[15] 陈奕柏, 柯才桐, 曹雄, 等. 平移变位模式下黏性土非极限主动土压力[J]. 暨南大学学报(自然科学与医学版), 2014, 35(4): 409-415. CHEN Yibo， KE Caitong，CAO Xiong，et al. Non-limit active earth pressure of cohesive backfill under translation mode[J].JournalofJinanUniversity(NaturalScience&MedicineEdition)，2014，35(4)：409-415.

[16] 章瑞文，徐日庆.土拱效应原理求解挡土墙土压力方法的改进[J].岩土力学，2008，29(4)：1057-1060. ZHANG Ruiwen, XU Riqing. Solution of problem of earth pressure on retaining wall calculated by method of soil arching effect[J].RockandSoilMechanics，2008，29(4)：1057-1060.

[17] 俞缙，周亦涛，蔡燕燕，等.基于土拱效应的刚性挡墙墙后主动土压力[J].岩土工程学报，2013，35(12)：2306-2310. YU Jin，ZHOU Yitao，CAI Yanyan, et al. Active earth pressure for rigid retaining wall considering soil arching effect[J].ChineseJournalofGeotechnicalEngineering，2013，35(12)：2306-2310.

(责任编辑 谭绪凯)

Non-limit Active Earth Pressure Against Inclined Rigid RetainingWall Considering Soil Arching Effect

ZHOU Yitao1, 2，WANG Xuemin2，JIANG Wenfang3，CAI Yanyan3

(1. College of Civil Engineering, Fuzhou University, Fuzhou 350116,Fujian, P.R.China; 2.Department of Transportation Engineering, Hebei University of Water Resources and Electric Engineering, Cangzhou 061001,Hebei, P.R.China； 3.College of Civil Engineering, Huaqiao University, Xiamen 361021,Fujian, P.R.China)

The non-linear relationship of lateral displacement and non-limit internal friction angle was introduced. By the stress relationship between inclined wall back and sliding cracking surface under non-limit state and the horizontal static equilibrium equation of horizontal micro sublayer unit, the non-limit slide cracking surface inclination was obtained and the non-limit active earth pressure calculation formula for inclined rigid retaining wall with soil arching effect under translating mode and the displacement considered. The parameter analysis results indicate that the increase of lateral displacement proportion causes the increase of inclination of non-limit sliding cracking face, decrease of non-limit active soil pressure coefficient and decerase of non-limit active soil pressure. The increase of inclination of wall back causes the decrease of inclination of non-limit sliding cracking face, decrease of non-limit active soil pressure coefficient and increase of non-limit active soil pressure. The non-limit active soil pressure decreases with the increase of internal friction angle of filled soil and wall soil friction angle. Compared with traditional method the proposed non-limit active soil pressure theory value fits better experimental values.

geotechnical engineering；inclination of non-limit sliding surface; the soil arching effect; non-limit active earth pressure; ratio of lateral displacement; inclined angle of wall back

10.3969/j.issn.1674-0696.2017.02.11

2015-07-01；

2016-02-10

国家自然科学基金项目(51308234)；河北省教育厅项目(QN2014149)；福建省自然科学基金项目(2014J01160)

周亦涛(1978—)，男，四川宣汉人，副教授，博士，主要从事岩土力学、岩土工程测试技术及地基处理方面的研究。E-mail：zhouytwr@163.com。

江文放(1991—)，男，福建漳州人，硕士，主要从事岩土力学与岩土工程方面的研究。E-mail：jiangwenfang@hqu.edu.cn。

TU432

A

1674-0696(2017)02- 061- 06