大跨径多塔斜拉桥恒载索力优化方法

周 云 岗

(同济大学建筑设计研究院(集团)有限公司，上海 200092)

大跨径多塔斜拉桥恒载索力优化方法

周 云 岗

(同济大学建筑设计研究院(集团)有限公司，上海 200092)

基于斜拉桥传统索力优化理论，提出3阶段优化算法。该算法以既定的合理成桥状态准则为目标，运用刚性支承连续梁法获得初始成桥状态，利用零位移法实现结构线形目标，以弯曲能量最小为目标，指定各种约束条件，利用ANSYS 优化模块中的1阶优化方法实施索力优化，获得目标成桥状态，求解过程中考虑几何非线性的影响。建立3～6塔主跨为1 400 m斜拉桥的有限元模型，利用参数化设计语言(APDL)编制计算程序，进行算例分析。结果表明：微调索力，结构变形改变量较小，而结构内力变化显著；索力优化前后，塔、梁恒载弯矩明显减小，结构内力和变形均能满足既定目标；运用该算法进行3～6塔斜拉桥成桥状态计算，结构内力和变形均能满足既定目标。

桥梁工程；多塔斜拉桥；索力优化；合理成桥状态；几何非线性

斜拉桥为超高次静定结构，影响其成桥内力状态主要因素有恒载分布、索力和边界支承反力等。研究表明[1]：斜拉索索力是确定合理成桥状态的关键因素。因此，进行索力优化研究具有重要的工程意义。

目前，索力优化方法大致可分为4大类[2-5]：①指定状态的索力优化；②无约束的索力优化；③有约束的索力优化；④影响矩阵法。利用任意一种方法，一般很难获得理想的结果[6]，常常几种方法组合使用。张建民等[7]以斜拉桥主梁和索塔的弯曲应变能为目标函数，以各斜拉索的索力为设计变量，结构应力及索力为约束条件，采用一阶分析法进行求解，用以确定成桥合理状态的索力；苏剑南[8]采用最小弯曲能量法初定近似合理的成桥状态，以该状态下部分斜拉索索力和主梁弯矩作为目标向，通过影响矩阵法求解所有斜拉索初张力；杨德灿等[9]以塔梁的弯曲和拉压应变能之和为目标函数，以斜拉索的初张力为设计变量，成桥索力和主梁钢混结合处的弯矩为约束条件，结合ANSYS 优化模块中的零阶和一阶方法进行求解；何旭辉等[2]运用影响矩阵原理求解斜拉桥合理成桥索力时，通常以结构弯曲能量或弯曲拉压应变能最小为目标状态，然后通过约束条件实现索力分布均匀；缪长青等[10]基于影响矩阵方法，导出了考虑交通车辆荷载和温度作用的影响矩阵表达式，并根据矮塔斜拉桥的结构特点建立相关的约束条件。这些学者基本以结构内力为优化目标进行索力计算，而且均针对传统双塔斜拉桥。

以结构内力和变形为优化目标，同时考虑多塔斜拉桥有限元分析特有问题，包括索塔平衡索力确定和梁端弹性压缩影响等，综合运用刚性支承连续梁法、零位移法和弯曲能量最小法，提出了3阶段优化算法，利用ANSYS 优化模块中的一阶优化方法进行求解，计算中考虑了各种非线性因素影响。

1 几何非线性分析方法

斜拉桥的几何非线性影响来源于：结构的大位移效应、主梁和索塔在巨大的轴压力作用下的P-Δ效应(即梁柱效应)及斜拉索的垂度效应。

采用ANSYS程序实现优化算法时，结构大位移效应采用大位移刚度矩阵考虑，P-Δ效应采用初应力刚度矩阵考虑，斜拉索的垂度效应采用8段杆单元法考虑[11]。

2 优化方法

2.1 合理成桥状态的确定准则

斜拉桥合理成桥状态是指结构内力状态趋向理想目标状态[12]。其确定准则主要有除个别斜拉索外，索力分布均匀；对钢主梁斜拉桥，主梁弯矩分布均匀，基本处于受压状态；索塔以轴向受压为主，弯矩趋于0；边墩和辅助墩无负反力，并有一定压力储备。

2.2 建模方法及优化目标

斜拉桥的目标线形主要指主梁线形和索塔线形，一般是已知的。建立有限元分析模型时，一般以目标线形确定有限元模型的节点位置，并采用相应方法计算构件的初始内力。若初始内力与目标状态下的内力一致，结构即处于理想成桥状态。可见，合理成桥状态计算就是寻找满足目标状态的一组构件内力。

根据合理成桥状态的确定准则和有限元分析模型特点，可得结构的优化目标为：①索力分布均匀；②主梁变形趋于0，即其弯矩呈刚性支承连续梁分布；③主塔变形趋于0，即其根部弯矩趋于0。负反力通常由压重或设置拉力支座来满足。

2.3 优化算法

3阶段优化法的基本思想是：首先根据目标线形建立有限元分析模型；然后进行结构找形；最后实施索力优化。计算流程如图1。

图1 3阶段优化算法流程Fig.1 Flow chart of three-stage optimization method

算法中：主梁轴向变形采用预压力解决，约束条件为xb<ξ1；主梁竖向变形通过调整索内力解决，约束条件为xv<ξ3；边塔水平变形，根据其拉索两侧水平力相等解决，约束条件为t1<ξ2。为保证边跨支座不出现拉力，设置边跨压重，其值为边跨索竖向分力与相应梁段重之间差值。

找形结束后，索力与理想索力相差不大，以结构弯曲能量最小为目标，微调索力，可进一步优化结构内力。索力优化阶段，索力设置调整范围，即设置约束条件Ti0(1-ξ)≤Ti≤Ti0(1+ξ)；其中：Ti0为初值找形完成时的索力；ξ为微调系数，一般为5%～10%。实施索力优化时，通常进行1～3次即可获得较佳的结果。

3 优化成果

3.1 计算模型

建立主跨为1 400 m的3塔斜拉桥为研究对象，验证3阶段优化算法。结构采用全漂浮体系，总体布置如图2。

图2 3塔斜拉桥立面布置(单位:m)Fig.2 Elevation of three-tower cable-stayed suspension bridge

塔、梁截面几何特性如表1。表1中：A为面积,Iy为面内抗弯惯距,Iz为面外抗弯惯距,Ix为抗扭惯距。主梁采用钢箱梁，标准断面如图3(a)。索塔采用混凝土桥塔，结构布置及断面如图3(b)。

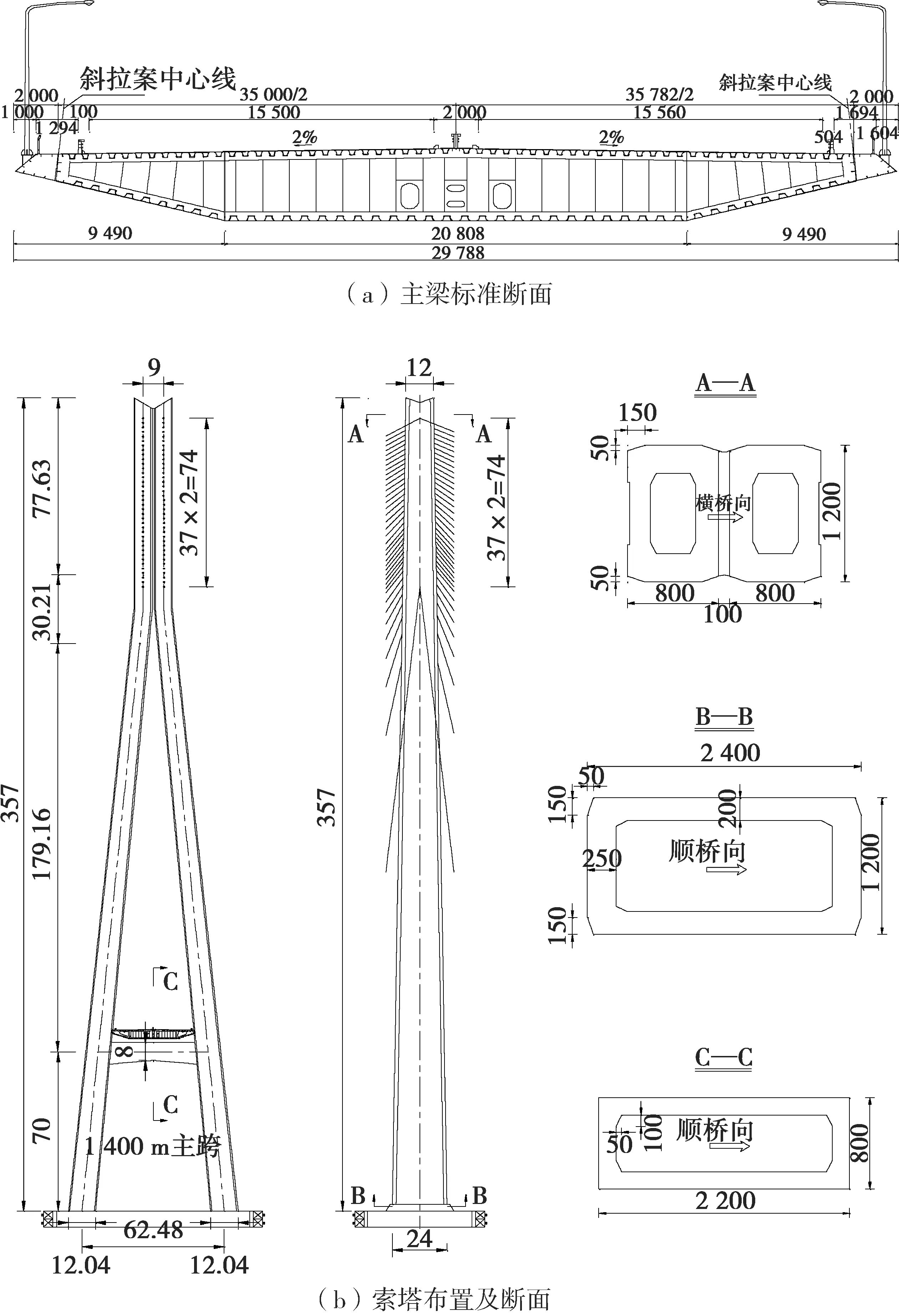
图3 塔、梁典型断面Fig.3 Section of town and beam

断面部位面积A/m2面内抗弯惯距Iy/m4面外抗弯惯距Iz/m4抗扭惯距Ix/m4主梁断面A断面B断面C断面D1．7222．1422．5612．8315．4877．1858．8739．938255．172298．405341．527368．15914．16718．79823．32725．680边塔塔顶塔底69．4140．21013．38958．8452．02590．41075．26819．4中塔塔顶塔底164．2355．04671．345118．01441．19006．13808．125947．3

结构的材料参考已有工程实例确定，主要构件的材料为：索塔采用C50混凝土；辅助墩采用C40混凝土；主梁采用Q370qd钢材；斜拉索采用Φ7 mm镀锌平行钢丝成品索，抗拉强度1 770 MPa，运营状态安全系数为2.5。

结构采用单主梁模式建立ANSYS分析模型，如图4。主梁和索塔采用空间梁单元(Beam44)模拟，拉索与主梁之间通过刚性杆相连，斜拉索采用只受拉杆多段杆单元(link10)模拟。塔、梁之间耦合横向自由度，墩、梁之间耦合横、纵向自由度。

图4 3塔斜拉桥计算模型Fig.4 Analysis model of three-tower cable-stayed bridge

进行成桥状态计算时，结构荷载设计值参照苏通长江大桥、泰州长江大桥和舟山连岛工程等大型桥梁的设计条件确定：一期恒载按材料密度确定；二期恒载按70 kN/m考虑。

3.2 计算成果

基于文中优化方法，笔者利用ANSYS二次开发功能，编制了计算程序。应用该程序进行恒载索力优化，成桥状态下，优化后的加劲梁挠度从-52.8～59.4 cm降为-14～1 cm；边塔顶纵向位移从-27.2 cm降为-6.8 cm，中塔从0.2 cm变为0.4 cm。主梁挠度如图5，考虑对称性，图5中仅示出左半桥。

图5 3塔斜拉桥主梁恒载挠度Fig.5 Deflection of beam under dead load of three-tower cable-stayed bridge

结构优化前后的内力状态如图6。由图6可知，在成桥作用下，主梁弯矩分布均匀且弯矩最大值仅为37 MN，呈刚性支承连续梁状态；除索塔两侧外，斜拉索力轴力分布较均匀，拉索应力大部分位于350～400 MPa之间；边塔塔根弯矩为300 MN，对应的弯曲应力为0.4 MPa；中塔弯矩最大值不超过88 MN，对应的弯曲应力为0.04 MPa。对比3阶段结构内力可得，斜拉索内力变化很小，主梁及边塔弯矩显著减小，中塔弯矩变大，但仍然很小，基本可忽略。

表2给出3塔斜拉桥3阶段优化结果。显然，通过索力优化后，结构受力状态得到很大改善。

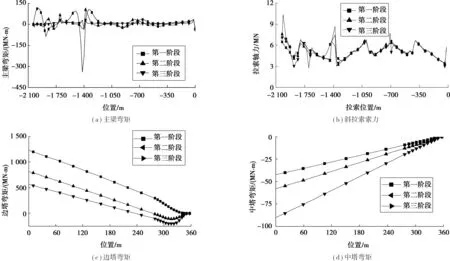
图6 3塔斜拉桥恒载内力Fig.6 Internal-force under dead load of three-tower cable-stayed bridge

构 件项目第3阶段优化成果第2阶段数值比例/%第1阶段数值比例/%主梁端部位移/m0．1110．062-44．10．076-31．8竖向挠度/m0．1350．18738．60．594340．0弯曲能量/(kN·m)150753403．647303063．0最大弯矩/(kN·m)37100107000189．84720001171．8上缘应力/MPa114．6126．510．4192．968．4下缘应力/MPa116．2134．716．0142．422．6索塔边塔顶位移/m0．0680．13394．10．272297．1中塔顶位移/m0．0040．003-36．30．002-53．8边塔根弯矩/(kN·m)56400081700045．01．23E+06118．7中塔根弯矩/(kN·m)-90100-57900-35．7-4．22E+04-53．1

上述分析表明，结构内力状态及线形满足既定的合理成桥状态指标。

4 多塔算例

应用文中方法确定3～6塔斜拉桥的合理成桥状态，进一步论证所提方法的有效性和适应性。多塔斜拉桥各方案立面布置如图7，考虑到结构对称性，图7中仅示出左半桥。

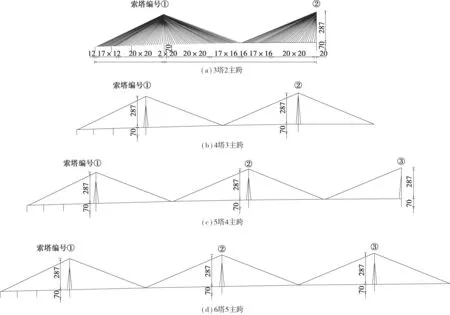
图7 多塔斜拉桥立面布置Fig.7 Elevation of multi-tower cable-stayed bridge

结构跨径布置、斜拉索间距及结构截面尺寸等参数同上。索塔编号由左向右依次为①，②，③，…，主跨跨径编号为该跨左侧索塔编号。

各方案均为全漂浮结构体系，辅助墩及索塔塔底固结；主梁与辅助墩顶之间耦合竖向和横向自由度，主梁与索塔横梁之间耦合横向自由度。此外，在所有辅助墩、过渡墩和索塔位置处，约束主梁扭转自由度。

采用文中方法确定各方案的合理成桥状态，主梁和斜拉索的最不利内力和变形如表3；索塔的最不利内力和变形如表4，表4中应力为弯矩产生的弯曲应力。

表3 主梁和拉索的恒载受力状态

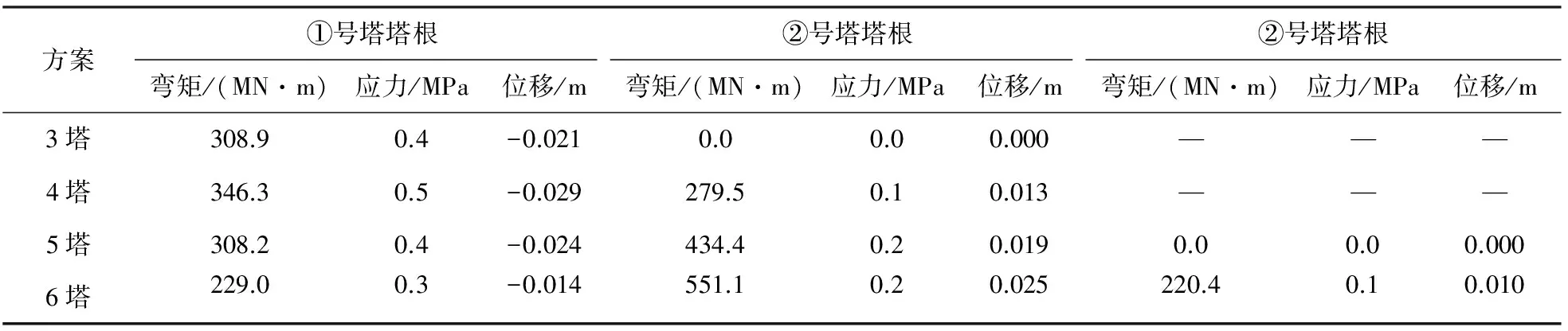
表4 索塔的恒载受力状态

由表4可知，各方案的主梁挠度最大约为0.15 m；塔顶位移最大约为0.025 m；主梁弯矩最大约为57 MN·m；弯曲应力最大约为29 MPa；拉索索力轴力最大约为8 MN；拉索应力约为545 MPa；塔根弯矩产生的弯曲应力均小于0.5 MPa，可忽略不计。

上述分析表明，结构内力状态及线形满足既定的合理成桥状态指标。

5 结 论

1)将刚性支承连续梁法、零位移法、弯曲能量最小法等方法组合起来，利用ANSYS一阶优化方法确定多塔斜拉桥合理成桥状态可以获得拟定的目标成桥状态。该方法兼顾结构的内力和变形，并考虑结构几何非线性的影响。经实例检验，该方法适应性强，收敛速度快。

2)确定多塔斜拉桥合理成桥状态时，必须考虑主梁轴向压缩变形。

3)微调斜拉索的索力对结构的内力状态影响明显，对线形状态影响较小。

[1] 张杨永，孙斌，肖汝诚．超千米级斜拉桥的恒载索力优化[J]．华南理工大学学报(自然科学版)，2009，37(6)：142-146． ZHANG Yangyong, SUN Bin, XIAO Rucheng. Optimization of cable force for cable-stayed bridges with ultra kilometer span under dead loads[J].JournalofSouthChinaUniversityofTechnology(NaturalScienceEdition), 2009, 37(6): 142-146.

[2] 何旭辉，杨贤康，朱伟．钢桁梁斜拉桥成桥索力优化的实用算法[J]．铁道学报，2014，36(6)：99-106． HE Xuhui, YANG Xiankang, ZHU Wei. Practical algorithm for optimization of cable forces in completion of steel truss girder cable-stayed bridges[J].JournaloftheChinaRailwaySociety, 2014, 36(6): 99-106.

[3] 张杨永，吴万忠，周云岗．斜拉桥索力精确模拟的矩阵分析法[J]．重庆交通大学学报(自然科学版)，2009，28(6)：979-981． ZHANG Yangyong, WU Wanzhong, ZHOU Yungang. Matrix analysis method for precise simulation of cable force of cable-stayed bridge[J].JournalofChongqingJiaotongUniversity(NaturalScience), 2009, 28(6): 979-981.

[4] 陈湛荣，刘琪，周水兴．中小跨径斜拉桥索力优化的“二阶段法”[J]．重庆交通大学学报(自然科学版)，2008，27(2)：181-184． CHEN Zhanrong, LIU Qi, ZHOU Shuixing. “Two stage method”of cable tension optimization for short/medium span cable-stayed bridges[J].JournalofChongqingJiaotongUniversity(NaturalScience), 2008, 27(2): 181-184.

[5] 刘益铭，刘大洋，刘山洪．基于MATLAB联合ANSYS的斜拉桥恒载索力优化[J]．重庆交通大学学报(自然科学版)，2013，32(6)：1111-1114． LIU Yiming, LIU Dayang, LIU Shanhong. Optimization of cable forces of cable-stayed bridges based on MATLAB and ANSYS software under dead loads[J].JournalofChongqingJiaotongUniversity(NaturalScience), 2013, 32(6): 1111-1114.

[6] 张文献，刘旭光，李东炜，等．斜拉桥成桥及施工阶段的索力优化[J]．东北大学学报(自然科学版)，2009，30(8)：1201-1204． ZHANG Wenxian, LIU Xuguang, LI Dongwei, et al. Optimizing cable tension during construction and completion of a cable-stayed bridge[J].JournalofNortheasternUniversity(NaturalScience), 2009, 30(8): 1201-1204.

[7] 张建民，肖汝诚．预应力混凝土斜拉桥空间非线性恒载索力优化[J]．计算力学学报，2008，25(1)：117-122． ZHANG Jianmin, XIAO Rucheng. Spatial nonlinear cable force optimum for a prestressed concrete cable-stayed bridge under permanent loads[J].ChineseJournalofComputationalMechanics, 2008, 25(1): 117-122.

[8] 苏剑南．厦漳跨海大桥北汊主桥合理成桥状态研究[J]．桥梁建设，2013，43(4)：44- 48． SU Jiannan. Study of rational completed bridge state of north main bridge of Xiazhang sea-crossing bridge[J].BridgeConstruction, 2013, 43(4): 44- 48.

[9] 杨德灿，章芳芳．考虑结合处弯矩限值的混合梁斜拉桥索力优化[J]．华中科技大学学报(自然科学版)，2010，38(8)：111-114． YANG Decan, ZHANG Fangfang. Optimizing completed cable-stayed bridge’s cable tensions with mixed stiffening girders when moment constraint condition at junction section considered[J].JournalofHuazhongUniversityofScienceandTechnology(NaturalScienceEdition), 2010, 38(8): 111-114.

[10] 缪长青，王义春，黎少华．矮塔混凝土斜拉桥成桥索力优化[J]．东南大学学报(自然科学版)，2012，42(3)：526-530． MIAO Changqing, WANG Yichun, LI Shaohua. Optimization of bridge-completing cable force for extradosed concrete cable-stayed bridges[J].JournalofSoutheastUniversity(NaturalScienceEdition), 2012, 42(3): 526-530.

[11] 孙斌．超千米级斜拉桥结构体系研究[D]．上海：同济大学，2008：38- 45． SUN Bin.StudyonStructuralSystemsinSuper-kilometerCableSupportedBridge[D]. Shanghai: Tongji University, 2008: 38- 45.

[12] 颜东煌，李学文，刘光栋，等．混凝土斜拉桥合理成桥状态确定的分步算法[J]．中国公路学报，2003，16(1)：43- 46． YAN Donghuang, LI Xuewen, LIU Guangdong, et al. Step-by-step arithmetic for the reasonable finished dead state of the concrete cable-stayed bridges[J].ChinaJournalofHighwayandTransport, 2003, 16(1): 43- 46.

(责任编辑 刘 韬)

Optimization Method of Cable Force for Large-Span Multi-Towerer Cable-Stayed Bridges under Dead Load

ZHOU Yungang

(Tongji Architectural design (group) Co., Ltd, Shanghai 200092, P. R. China)

Based on optimization method of cable force for traditional cable-stayed bridge, three-stage optimization algorithm is proposed. In order to realize the target according to the criterion of reasonable completed status, the algorithm using rigid supported continuous beam method to calculate the initial cable force of these bridges. Then, using zero displacement method, the algorithm makes structural displacement be close to zero. Finally, taking the minimum bending energy as the optimization object and setting constraint conditions according to the reasonable finished dead state, the models are solved by the first order optimization method of ANSYS to obtain reasonable dead state, with geometric nonlinearity being considered. Four finite element models of three-tower to six-tower cable-stayed bridge with the span of 1400m are established and are used to establish mathematic optimization model for cable force with the algorithm realized by using ANSYS parametric design language (APDL). Calculated results show that: fine-tuning cable force, structure displacement slightly changes, yet the internal force remarkably changes. After the optimization, the bending moment of girder and pylon significantly decrease, and meet desired goal. Using the algorithm to analysis, internal force and deflection of all structures can meet desired goal.

bridge engineer; multi-tower cable-stayed bridge; cable force optimization; reasonable finished dead state; geometric nonlinearity

10.3969/j.issn.1674- 0696.2017.02.01

2015- 04- 02；

2015- 08-11

周云岗(1980—)，男，江苏淮安人，工程师，博士，主要从事大跨度桥梁设计理论方面的研究。E-mail：0tjrocket@tongji.edu.cn。

U448.225

A

1674- 0696(2017)02- 001- 06