双足行走机器人运动轨迹规划

林保蛟，华云松，顾岩秀

(上海理工大学 光电信息与计算机工程学院，上海 200093)

双足行走机器人运动轨迹规划

林保蛟，华云松，顾岩秀

(上海理工大学 光电信息与计算机工程学院，上海 200093)

针对双足行走机器人数学描述复杂，分析较为困难等问题，采用五次多项式插值法规划机器人的关节运动轨迹，为每个关节设计相应的轨迹，达到运动学求解过程中所得出的转动角度，使机器人从起始位置运动到某个规定的目标位置，实现机器人在作业空间的行走。通过对机器人运动轨迹的分析，结果表明了用五次多项式插值法是一种规划双足机器人步态行走的较好方法，得到的机器人关节运动轨迹图更加光滑平稳。

双足机器人；运动轨迹；五次多项式插值法

双足行走机器人是一个多自由度、非线性、具有复杂动力学特性的多体系统, 21世纪以来，国内外许多个人和单位相继推出了各自研制的双足机器人，各国研究学者认为机器人技术对未来新兴产业的兴起和发展具有重要意义[1]。因其外形和功能形似人类。适合在人类生活和工作的环境中与人类协同工作[2-3]，还可代替人类在危险环境中作业，拓宽人类的活动空间[4]，有高度的适应性与灵活性。实现稳定步行是双足机器人研究的首要任务[5]，合理的步态规划是机器人稳定步行的基础。

欧盟在第七框架计划(FP7)中规划了“认知系统与机器人技术”研究、美国启动了“国家机器人计划”、日本和韩国则针对服务型方面的机器人制定了主要的研究策略。最具代表性的有日本早稻田大学加藤一郎教授研制的WAP系列样机,日本东京大学研制的HS、H6型仿人型双足步行机器人等。我国同时在国家高技术研究发展计划(863计划)、国家科技重大专项、国家自然科学基金等规划中对机器人技术的研究与发展应用给予重视[6]。

在这段期间，有很多对双足行走机器人的行走模式的分析[7-9]和对双足行走机器人进行综合性研究，与信息和技术等有着密切的联系，是机械学、仿真学、运动学及控制工程学等多种基础学科的高度融合。目前，双足行走机器人在医学上应用比较广泛，尤其是康复医学领域。从长远的角度来看，双足机器人在核电站、宇宙探索、无人工厂、康复医学以及艺术、大众服务行业等领域都有非常广阔的应用前景[10-11]。本文通过对机器人运动轨迹规划进行分析，采用五次多项式插值法规划出双足机器人关节在整个步行周期内的平滑运动轨迹。

1 双足机器人轨迹规划

机器人路径描述的是其位置形状的一个特定序列，因此路径与机器人位形的时间无关。而轨迹则与机器人在不同时刻到达路径中的哪个部分相关，强调时间性[12]。图1中机械腿没有位姿具体要求，从A点经过B点再运动到C点，其路径相同，而根据运动的时间不同，速度和加速度不同，所以相应的轨迹也不同。

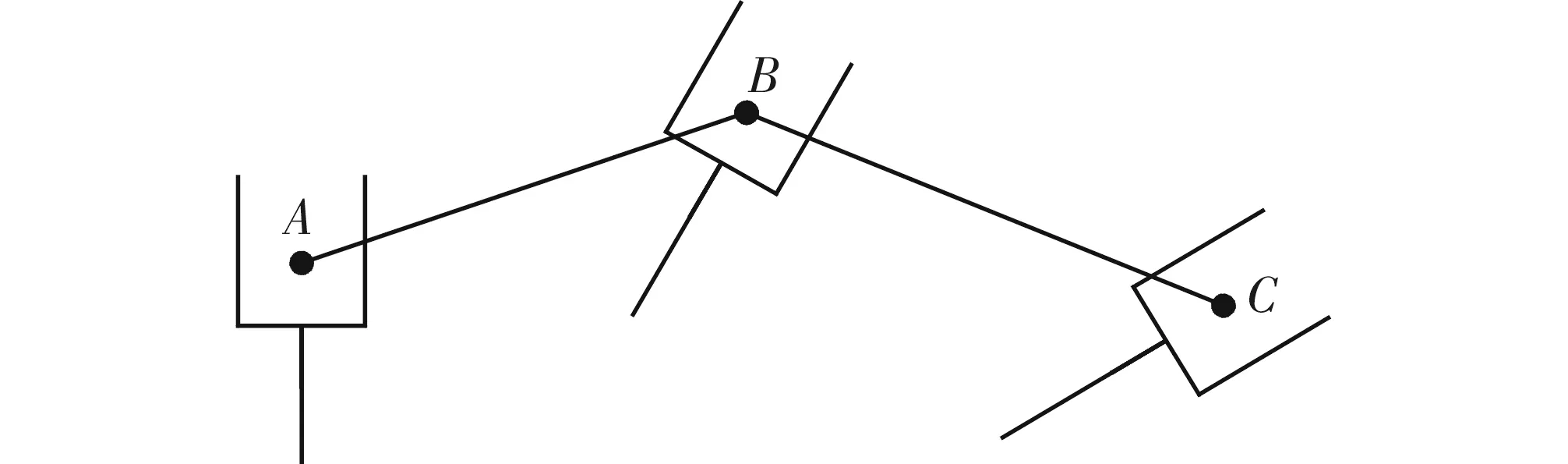
图1 机器人在路径上的运动原理图

以两自由度机械腿为例，假设机械腿要沿从A点到B点的路径运动。A点的位形为α=20°，β=30°，B要到达的点的位置为α=40°，β=80°。已知机械腿关节运动的最大角速度为10°/s，完成从点A到点B任务的一种常见方式为：两关节进行最大速度运动。关节1用时2 s，关节2用时5 s，如图2所示，可见机械腿的运动路径不规则，末端走过的距离也不均匀。

图2 机械腿关节空间轨迹

若两个关节要同步运动，可将关节的运动参数用一个公共因子归一化，来成比例的减慢关节1的运动。由图3可看出，虽得到的路径仍不规则，但两个关节的运动轨迹比之前均匀。

若希望机械腿能从A点到B点沿直线运动，如图4所示。(1)画一条直线连接A点和B点；(2)将直线AB等分成5份，得到4个等分点；(3)计算出各分点所

对应的αβ值，此过程称为A点和B点之间插值运算[13]。图4可以看出，路径是直线时，其关节角变化并不均匀。故需要计算更多的关节点来提高机械腿的沿循精度。

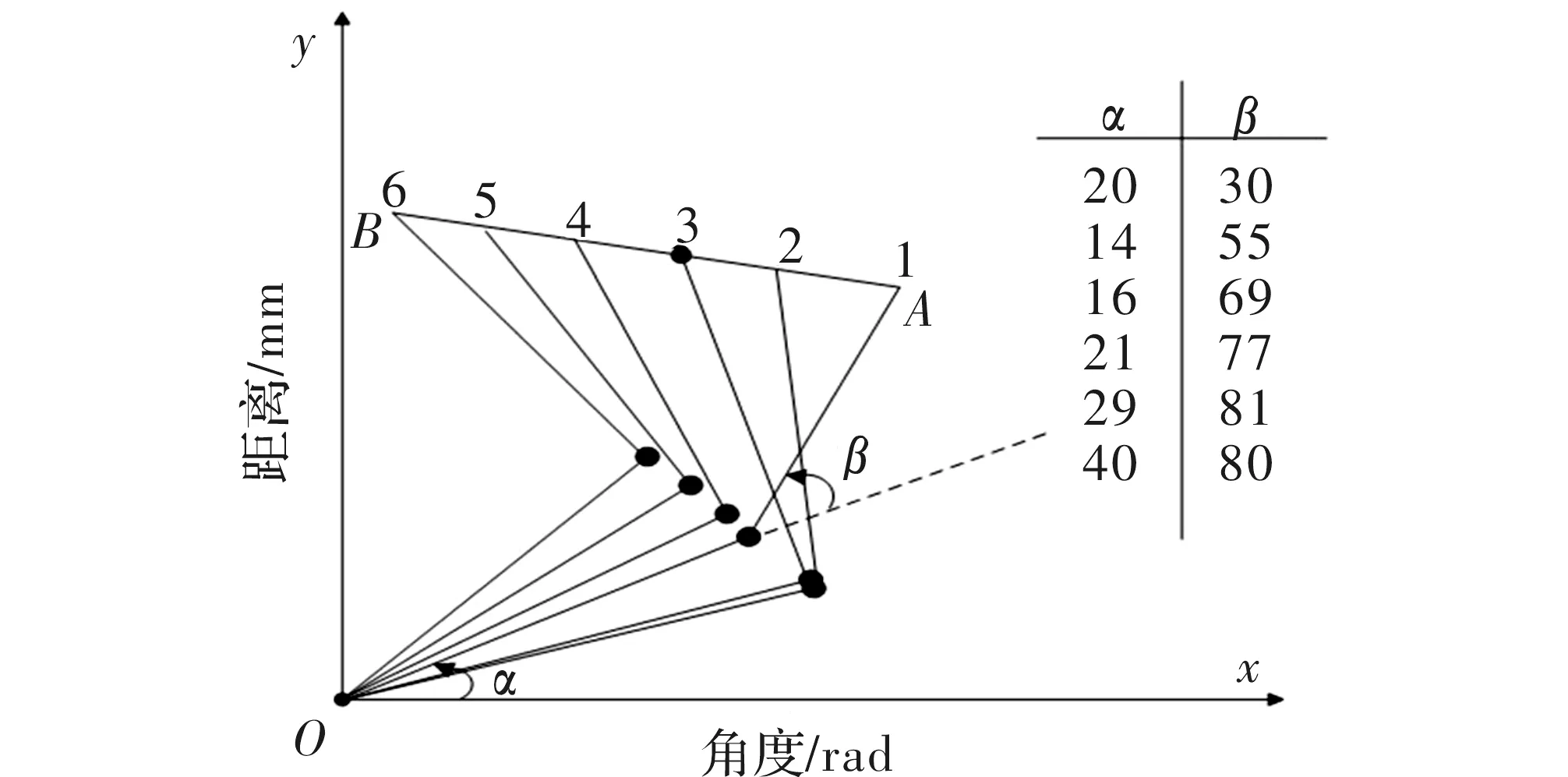
图3 机械腿关节空间的归一化运动轨迹

图4 机械腿关节插值规划的轨迹

分析本文机器人实际运动时的轨迹，如图5所示。当左脚迈进时，右腿上右脚脚掌看做固定构件，腿部向前运动；左腿上把大腿终端看做固定构件，脚掌带动小腿及大腿关机运动。为了保持机构稳定性，机器人行走时，应当保持载物平台高度不变，也可使用插值法进行规划。

图5 行走原理图

2 轨迹规划的方法

轨迹规划通常是在关节空间和笛卡尔空间进行。进行轨迹规划，首先运用逆运动学求解将路径点转换为关节矢量角值[14]。然后对各关节建立一个关于时间的函数，其之间互不影响，对关节函数进行一阶和二阶求导，得到机器人各关节的运动角速度和角加速度，控制机器人从起始位置经过路径点到达终止位置，且各关节到达路径点的时间相同。

描述空间轨迹路径点，需要建立两个坐标系，表示其之间的相互关系。按以下步骤生成关节空间的轨迹：(1)路径点位置转化为关节矢量角度值；(2)根据角度值拟合得到所有关节的平滑函数；(3)按顺序平滑地经过所有路径点最终到达终点。

关节空间进行轨迹规划的方法众多，主要包括高次多项式插值法、用抛物线过渡的线形插值法、样条曲线插值法等，根据不同的约束条件选用不同的插值规划方法[15]。

3 五次多项式插值的轨迹规划

当双足行走机器人的初始位姿给定时，可使用逆运动学求解的方法求解所有期望的位置和姿态[16]。求解平滑插值函数θ(t)，使它满足给定的已知条件。假设某一关节初始状态的时间为ti，角度为θi，终止状态的时间为tf，角度为θf。再增加两个加速度约束条件，可得边界条件的6个未知量。设五次多项式函数为

θ(t)=a0+a1t+a2t2+a3t3+a4t4+a5t5

(1)

其系数必须满足6个约束条件如式(2)

(2)

求解上述方程组得式(3)

(3)

假设机器人的关节1在前1 s内从初始角0°运动到15°，后1 s从16°运动到40°，行走机器人开始运动瞬间加速度为10°/s，行走机器人停止运动瞬间末端加速度为-10°/s。将初始和末端边界条件代入式(3)得前1 s未知参数数值。

(4)

同理得到后1 s未知参数数值如式(5)

(5)

将式(4)中所得参数值带入式(1)和式(2)，得出前1 s的角度位置、角速度、角加速度的五次多项式方程如式(6)

(6)

同理可得后1 s的运动方程如式(7)

(7)

用Matlab编程得到该关节的角度位置、角速度、角加速度图如图6～图8所示。

图6 五次多项式插值的角位置图

图7 五次多项式插值的角速度图

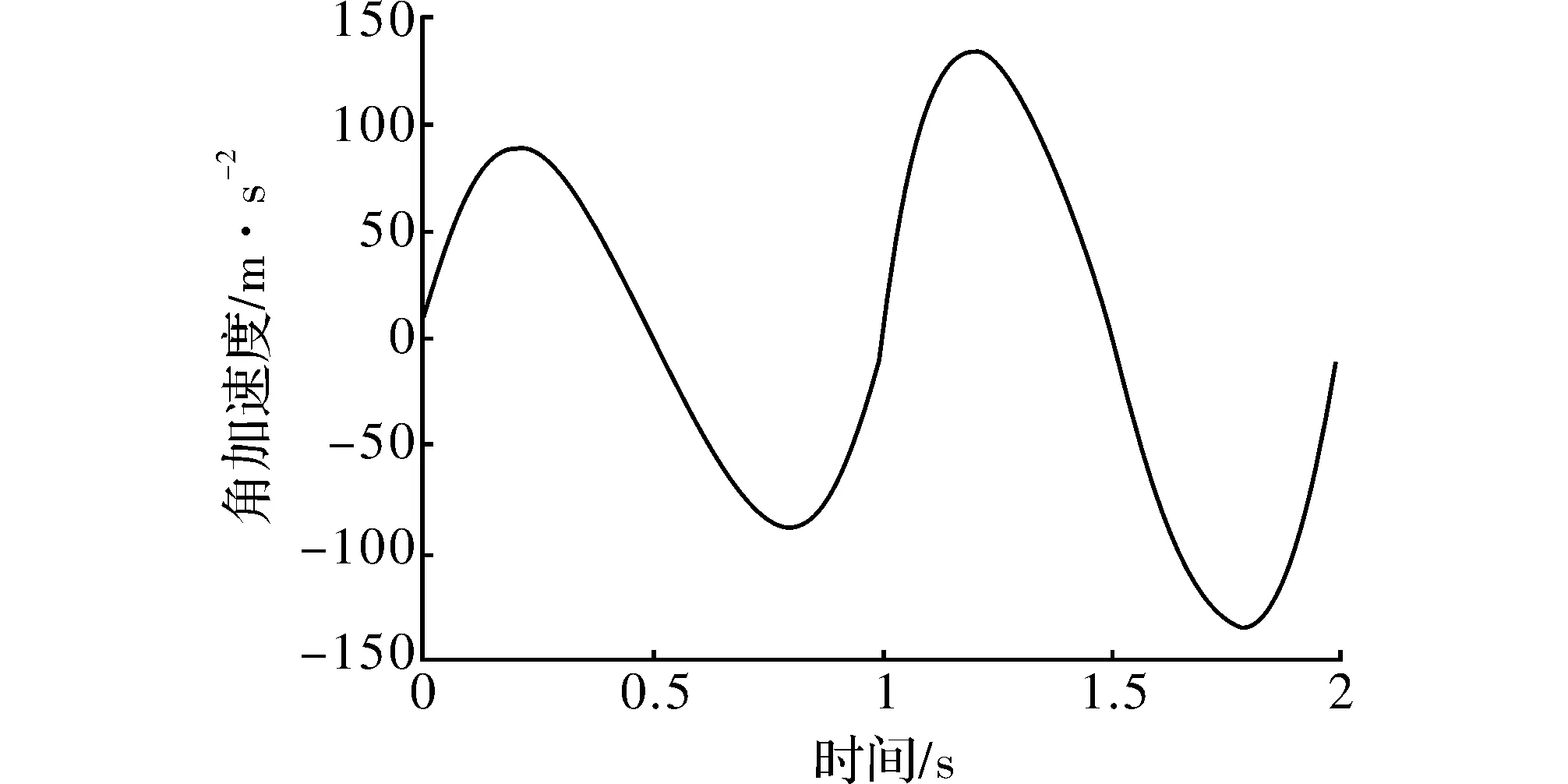
图8 五次多项式插值的角加速度图

4 结束语

本文通过对双足机器人轨迹进行规划，采用五次多项式插值法规划的机器人关节运动轨迹图更加光滑平稳，在加速度曲线对比中体现明显，而加速度是直接能反应运动平稳的重要参数，加速度的变化快慢直接影响机器人的运动效果，影响载物的平衡。Matlab[17]的仿真结果表明，采用五次多项式插值进行轨迹规划的方法更有效。

[1] 梁栋,尹晓红,王梦晴.移动机器人研究现状及发展趋势[J].科技信息,2014(9):33-33.

[2] Hirai K, Hirose M,Haikawa Y,et a1.The development of honda humanoid robot[C].Leuven,Belgium:Proceedings of the IEEE International Conferenee on Robotics and Automation,l998.

[3] Hirai K. Current and future perspective of honda humanoid robot[M].Robotics Research. Springer London, 1998.

[4] 陈恳,付成龙.仿人机器人理论与技术[M].北京:清华大学出版社,2010.

[5] 高佳.双足机器人动态行走研究[D].北京:北京信息科技大学,2008.

[6] 谭民,王硕.机器人技术研究进展[J].自动化学报,2013,39(7):963-972.

[7] Mogeer T.Passive dynamic walking[J].Int J Robot Res,1990,9(2):62-82.

[8] Kaiita S,Yamaura T, Kobayashi A.Dynamic walking control of a biped robot along a potiential energy conserving orbit[J].IEEE Transactions on Robot Automat, 1992,8(4): 431-438.

[9] 杨东超,汪劲松,刘莉,等.基于ZMP的拟人机器人步态规划[J].机器人,2001,23(6):504-508.

[10] 黄晶.拟人足球机器人运动学分析[D].天津:天津大学,2004.

[11] 韩亚丽,王兴松.行走助力机器人研究综述[J].机床与液压,2008,36(2):165-169.

[12] Grasser F,D’Arrigo A,Colombi S, et al. JOE: A mobile, inverted pendulum[J].IEEE Transactions on Industrial Electronics,2002,49(1):107-114.

[13] Nasrallah D S,Michalska H,Angeles J,et al.Robust posture control of a mobilewheeled pendulum moving on an inclined plane.[C].CA,USA:IEEE International Conference on Mechatronics,2006.

[14] Liu D,Sun H,Jia Q.Stabilization and path following of a spherical robot[C].Xi’an:IEEE Conference on Robotics, Automation and Mechatronics,IEEE,2008.

[15] 张升.四自由度机械手轨迹规划及运动控制[D].西安:长安大学,2012.

[16] Swevers J,Verdonck W,Schutter J D. Dynamic model identification for industrial robots[J].IEEE Control Systems,2007,27(5):58-71.

[17] 张志涌.精通Matlab 6.5版[M].北京:北京航空航天大学出版社,2003.

Motion Trajectory Planning of Biped Walking Robots

LIN Baojiao，HUA Yunsong，GU Yanxiu

(School of Optical-Electrical and Computer Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China)

In view of the complex mathematical description and difficult analysis of biped walking robots, quintic polynomial interpolation is introduced into the motion trajectory planning of the biped robot, with corresponding trajectory designed for each joint to reach the kinematics rotational angle, making the robot walk from the starting position to a predetermined target position. The robot trajectory analysis shows smooth motion trajectory of the biped robot.

bipied robot; plan motion trajectory; quintic polynomial interpolation

2016- 03- 31

林保蛟(1991-)，男，硕士研究生。研究方向：精密仪器及机械。

10.16180/j.cnki.issn1007-7820.2017.02.012

TP242

A

1007-7820(2017)02-045-04