运算题：分步解题，完满得分

运算题：分步解题，完满得分

曹 焱

中考中“数与式”的运算题属于必考的题型之一，在阅卷评分标准中一般分步得分，因此在解“数与式”的运算题时若能正确按步骤解题，踩准得分点，往往会少失分，直至不失分，下面举例说明.

一、有关实数、根式运算题

例1 （2016·山西）计算：（-3）2-

【分析】本题中先算乘方、负整数指数幂、二次根式、零指数幂的运算，再将这些结果相加减.

解：原式=9-5-4+1……（4分）

=1.……（5分）

【点评】从评分标准中我们可以看出，第一步正确得出乘方、负整数指数幂、二次根式乘法、零指数幂的结果将得4分，最后一步得1分，因此记牢乘方、二次根式运算法则，负整数指数幂、零指数幂等公式是解题的关键.

二、有关整式运算题

例2（2016·三明）先化简，再求值：（ab）2+b（3a-b）-a2，其中a=

【分析】本题先算完全平方公式、单项式乘多项式，再进行整式的加减，最后再代入求值.

解：原式=a2-2ab+b2+3ab-b2-a2……（4分）

=ab.……（6分）

……（7分）

【点评】从评分标准中我们可以看出，只要将完全平方及单项式乘多项式运算正确即有一半的分数，体现了中考对基本能力的重视；另外在化简求值问题中，按要求将数字正确代入字母也有分数，这些需要同学们在平时训练时格外重视.

三、有关分式运算题

【分析】本题先算分式的除法，再算分式的加减，最后将x=-1代入求值.

……（2分）

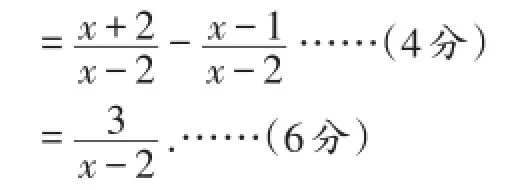
【点评】从评分标准中可以看出，分式的混合运算根据运算顺序先算乘方，再算乘除，最后算加减，当没有乘方时，先把除法转化为乘法也有2分，正确得出分式的乘法运算再得2分，算出正确结果得2分，层层递进，因此解题时严格按照步骤是相当必要的，也是避免失分的不二方法.

通过以上三例，同学们可以看到：在数与式的运算中，按步骤、按运算法则正确运算就能保证考试中最大限度地不失分.在平时的训练中，同学们可要记住哦！

小试身手

2.（2016·襄阳）先化简，再求值：（2x+1） ·（2x-1）-（x+1）（3x-2），其中x=

（作者单位：江苏省海门市实验初级中学）

（关注公众号，回复“2017年3月数学”查答案）