土−结构相互作用下单层柱面网壳振动台试验及数值分析

刘毅，薛素铎，王国鑫，李雄彦



土−结构相互作用下单层柱面网壳振动台试验及数值分析

刘毅1, 2，薛素铎2，王国鑫2，李雄彦2

(1. 中车建设工程有限公司，北京，100078；2. 北京工业大学建筑工程学院，北京，100124)

基于设计长度×宽度×高度为7.7 m×3.2 m×1.2 m的模型箱，以长度×跨度为1.8 m×1.8 m的单层柱面网壳为研究对象，设计实现土−独立基础−单层柱面网壳结构振动台试验，研究不同地震波输入下土−独立基础−单层柱面网壳结构体系地震响应的规律，同时采用整体有限元法建立振动台试验的有限元模型，与试验结果进行对比分析。研究结果表明：考虑土−结构相互作用时，土−独立基础−单层柱面网壳结构体系的试验结果与模拟结果变化规律基本一致，土−结构相互作用下基础底部的加速度峰值响应较自由场加速度峰值响应增大；土体与基础之间滑移和提离现象及模型箱的刚度是影响试验结果与模拟结果差距的主要因素，尤其是随着振动次数增多，土体与基础之间的非线性接触更加显著；地震波频谱特性是影响土−独立基础−单层柱面网壳结构体系地震响应的重要因素，在试验设计时应当尽量避开结构体系与地震波主频一致而发生共振现象，否则造成试验结果失真。

单层柱面网壳结构；土−结构相互作用；振动台试验；数值模拟；地震响应

大跨空间结构由于自身的复杂性和特殊性以及抗震设计中软件的局限性，在抗震设计中常将上部屋盖结构、下部支承结构、基础及地基分开设计，这种设计方法的缺陷和不足已在1995年日本阪神地震[1]、2008年汶川大地震[2]等数次地震中体现出来。近些年已有学者开始研究大跨屋盖结构与支承体系之间的协同工作问题[3−8]，然而，这些研究大都忽略了地基土与整个上部结构的相互作用问题。对大跨空间结构土−结构动力相互作用问题的研究很有必要。现有的对 土−结构相互作用下大跨空间结构抗震性能的研究都以数值分析为主。薛素铎等[9−11]采用集总参数法研究了土−结构相互作用下网架结构和网壳结构的抗震性能；楼梦麟等[12−13]采用整体有限元法研究了土−结构相互作用下双层柱面网壳结构、正放四角锥网架的抗震性能。刘毅等[14−17]采用集总参数法研究了协同工作条件下地基土对单层球面网壳结构动力性能影响，同时采用整体有限元法研究了土−结构动力相互作用下网架结构动力性能。现阶段关于土−结构相互作用下大跨空间结构振动台试验的研究很少，尤其考虑到大跨空间结构由于跨度大、土体的边界效应问题，普通振动台台面尺寸难以满足振动台试验要求。本文作者基于北京工业大学的九子台台阵体系，设计实现土−独立基础−单层柱面网壳结构振动台试验，该试验通过设计1个长度×宽度×高度为7.7 m×3.2 m×1.2 m的刚性模型箱和1个长度×跨度为1.8 m×1.8 m的单层柱面网壳，研究不同地震波输入下土−结构相互作用对土−独立基础−单层柱面网壳结构体系地震响应的影响，同时采用整体有限元法建立振动台试验的有限元模型，与试验结果进行对比分析。

1 振动台试验模型设计

本试验选用北京工业大学九子台台阵体系进行，其具体参数如表1所示，试验选用九子台阵体系中的4个子台，且4个子台按“一”字型分布，采用12个作动器，实现4台阵联体振动。

1.1 网壳模型设计

考虑到大跨空间结构土体边界效应、跨度大、振动台尺寸、试验为探讨土−结构相互作用下空间网格结构的地震响应规律等，局限于试验室条件试验模型未按照相似比例进行完全缩尺，而是根据试验室现有条件进行设计。上部结构为四点支承单层柱面网壳，网壳长度为1.8 m，跨度为1.8 m，矢跨比为1/4，柱高为0.5 m，采用焊接实心球，球直径为160 mm，纵向边梁截面直径×厚度为32 mm×3 mm，横向边梁截面直径×厚度为25 mm×2.5 mm，其他杆件截面直 径×厚度为20 mm×3 mm，柱截面直径×厚度为 60 mm×2.5 mm，钢材为Q235；采用独立基础形式，在基础内预埋螺栓，柱与网壳、柱与基础之间采用螺栓连接。钢材力学参数通过6组钢管拉伸试验拟合得到，其应力−应变曲线如图1所示。

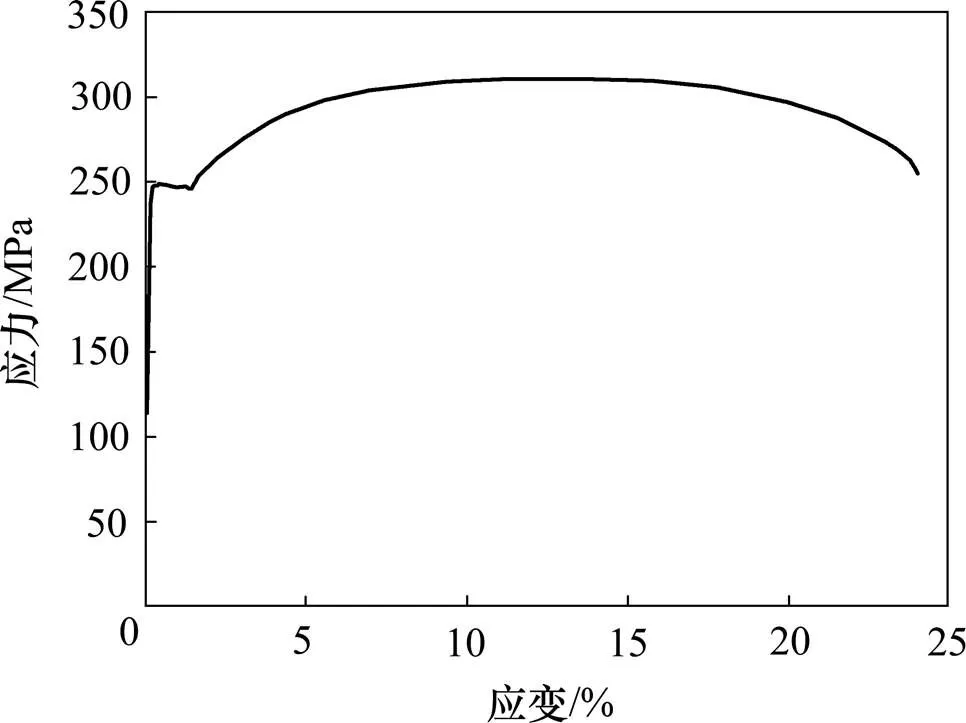
图1 钢材应力−应变曲线

1.2 模型箱设计

根据史晓军等[18]对不同模型箱的比较，对于刚性箱，在进行纵向水平地震激励时距离箱体侧壁0.5 m左右的影响已较小，采用刚性模型箱时,则在振动方向上的箱体长度应大于其高度的4倍[19]，LIU等[20−21]采用人工边界计算时，在局部场地周边扩大3倍以上即可获得很好的精度。因此，结合刚性箱边界效应和网壳模型尺寸，采用等边角钢∠70×5，∠70×10，∠70×15以及20 mm厚橡胶板设计完成长度×宽度×高度为 7.7 m×3.2 m×1.2 m的刚性模型箱，箱体边界内衬 20 cm厚的泡沫板以减小模型箱效应，模型箱周边和底部黏有混凝土颗粒以防止土体与箱体间滑动。

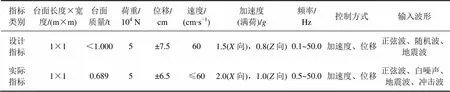
表1 九子台阵系统指标

1.3 模型土及基础

试验用土取自在建的北京地铁14号线北京工业大学地铁站附近土体。用环刀法取六组原状砂土，采用烘干法得到土体的质量含水率为7.38%，取样土体的容重为17.54 kN/m3，通过筛分试验测得砂土中粒径大于0.25 mm的颗粒质量分数占50%以上，达到75%，属于中砂范围。土体的参数通过直剪法和动三轴试验得到，如表2所示。

基础采用独立基础，基础高度为20 cm，基础底面长度和宽度均为25 cm，配有直径为6 mm的受力筋和箍筋。混凝土采用C25，混凝土弹性模量为2.72×104MPa，泊松比为0.167，密度为2 420 kg/m3。基础与土体的摩擦因数为0.42。

综上所述，可设计出实现土−独立基础−单层柱面网壳结构振动台试验，考虑到网壳结构侧向刚度的强弱及土体的边界效应，将网壳结构的跨度所在方向与箱体的长度方向平行布置在箱体的中心位置。

表2 土体参数

2 试验工况

2.1 地震波工况

根据GB 50011—2010“建筑抗震设计规范”中第5.1.2条规定，选用Kobe波和Northridge波两条实际强震记录和上海人工波1条人工模拟的加速度时程曲线作为输入加速时程。由于北京工业大学九子台台阵位移控制最大值为7.5 cm，实际为6.5 cm，若输入地震波原波则会使振动台位移超限，因此，根据振动台参数对输入的地震波进行滤波处理。滤波后输入的加速度时程曲线和相应的反应谱曲线如图2所示。

根据振动台调试确定试验最大输入加速度为0.40，同时结合“建筑抗震设计规范”将加速度峰值PG依次调整为0.14，0.22和0.40(1=9.806 65 m2/s)进行输入。地震波输入方向为沿箱体长度方向进行输入。由于地锚的约束问题、九子振动台本身的系统误差、4个子台存在局部非一致性等，致使九子台阵台面响应出的地震波峰值较输入值小，如表3所示。随着输入地震波强度的增大误差逐渐增大，这主要是多次振动致使地锚松动引起的。

2.2 传感器布置

试验对单层柱面网壳节点位移、加速度和杆件应变进行测量，图3所示为各类传感器布置图。位移测点布置在单层柱面网壳上，共8个位移测点，通过搭制脚手架用拉线位移传感器测量动位移。加速度传感器布置在单层柱面网壳节点、柱顶部、底部，独立基础顶部、底部，土体以及振动台台面上，共计22个测点，试验采用压电式传感器对土−独立基础−单层柱面网壳结构体系加速度进行量测。应变测点布置在单层柱面网壳的直杆、斜杆及边梁上，共计20个测点，上下对称布置，采用应变片测量应变。

图3 传感器布置

3 振动台试验结果与数值模拟结果对比分析

基于文献[16]中精细化模型基本理论，从理想状态角度出发，按照试验模型建立独立基础−土−单层柱面网壳相互作用的精细化模型，将基础和自由场地震响应、网壳节点加速度、网壳节点位移、网壳杆件应变的模拟结果与试验结果进行对比，其中在数值模拟中选用四子台阵台面上采集到的试验地震波进行输入，探究独立基础−土−单层柱面网壳结构相互作用体系地震响应规律。

3.1 基础和自由场地震响应分析

试验测定了PG为0.11，0.16和0.30地震输入下独立基础和自由场土体表面的地震响应。表4所示为不同PG输入下独立基础和自由场土体的PG。为了便于考察土−结构相互作用对单层柱面网壳体系中基础的影响，用PG增大幅度来衡量，定义为

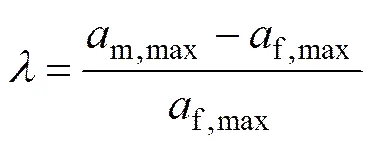
在考虑土−结构相互作用下，由表4可以看出：

1) 基础底部和自由场表面加速度峰值的试验值和模拟值基本能够吻合，在不同地震波输入下大部分工况相对误差在20%之内。

2) 随着输入地震动强度的增大，试验值与模拟值之间相对误差成增大趋势，这是由于随着振动次数的增多，试验中的土体与基础之间产生了较大的缝隙，使得土体与基础产生了滑移和提离现象，呈现出二者之间接触的非线性。

3) 基础底部的加速度峰值响应较自由场加速度峰值响应增大，增大5%~30%，这是地震波在由土体底部向土体表面传播过程中，在土体表面产生的反射和叠加效果引起。

4) 不同地震波作用下，基础底部和自由场加速度峰值存在差异，这是由不同地震波的频谱特性引起。其中，上海人工波作用下基础和自由场土体的加速度峰值较Kobe和Northridge波峰值偏大，这是由于上海人工波的主频与整体土−结构相互作用下单层柱面网壳体系的主频较接近，二者发生了共振。

3.2 网壳节点加速度响应

为研究不同地震波作用下土−独立基础−单层柱面网壳结构节点加速度响应规律，表5所示是PG为0.11，0.16和0.30输入下网壳节点1~6加速度峰值的试验值和模拟值的对比。图4所示是PG为0.11时网壳节点4在不同地震波输入下加速度时程曲线的试验值和数值模拟值的对比曲线。

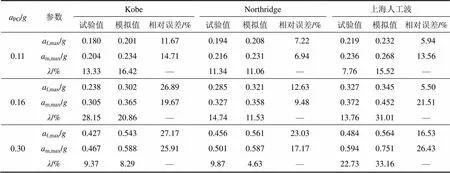
表4 基础与自由场加速度峰值试验值与模拟值对比

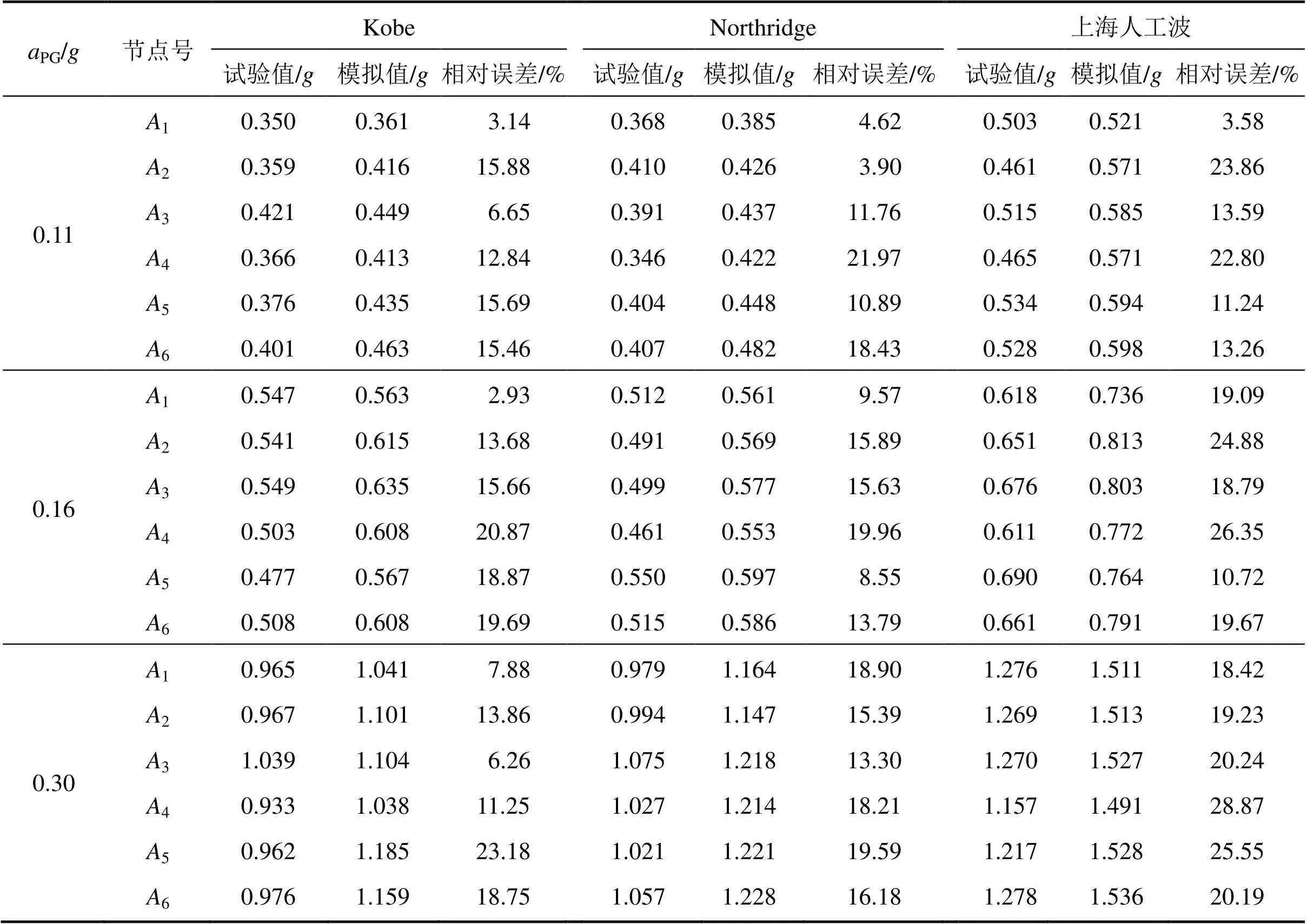
表5 网壳节点加速度峰值试验值与模拟值对比

对比分析表5和图4可以看出：

1) 在不同工况下，网壳所有测点的加速度峰值的试验值和模拟值的误差基本在20%之内，其中上海人工波的误差偏大，这是上海人工波的主频与相互作用体系频率一致发生共振所致。

2) 在不同地震波输入下，网壳节点加速度的试验时程曲线与模拟时程曲线的波形和相位基本吻合、变化规律一致。

3) 随着输入地震波强度的增大，网壳节点的加速度峰值试验结果与模拟结果误差增大，这是由于试验振动次数的增多，试验中的土体与基础发生了提离、滑移现象，土体与基础之间产生缝隙，约束变弱，接触非线性增强。

3.3 网壳节点位移响应

为研究不同地震波作用下土−独立基础−单层柱面网壳结构节点位移响应规律，表6所示是PG为0.11，0.16和0.30地震输入下网壳结构节点1~6位移最大值的试验值与模拟值对比。图5所示是PG为0.11时不同地震波输入下网壳节点4位移时程曲线的试验曲线与模拟曲线。

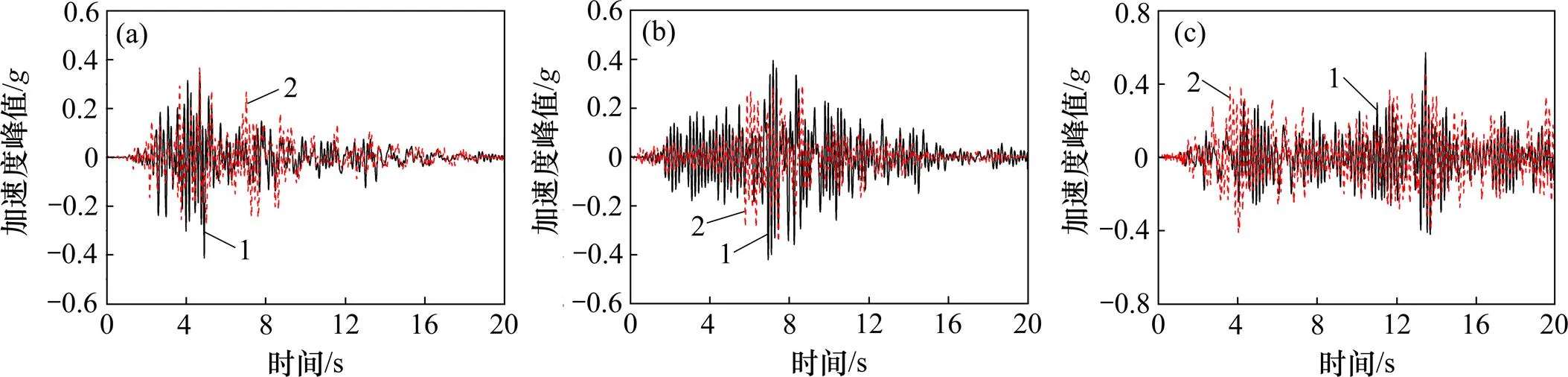
(a) Kobe；(b) Northridge；(c) 上海人工波

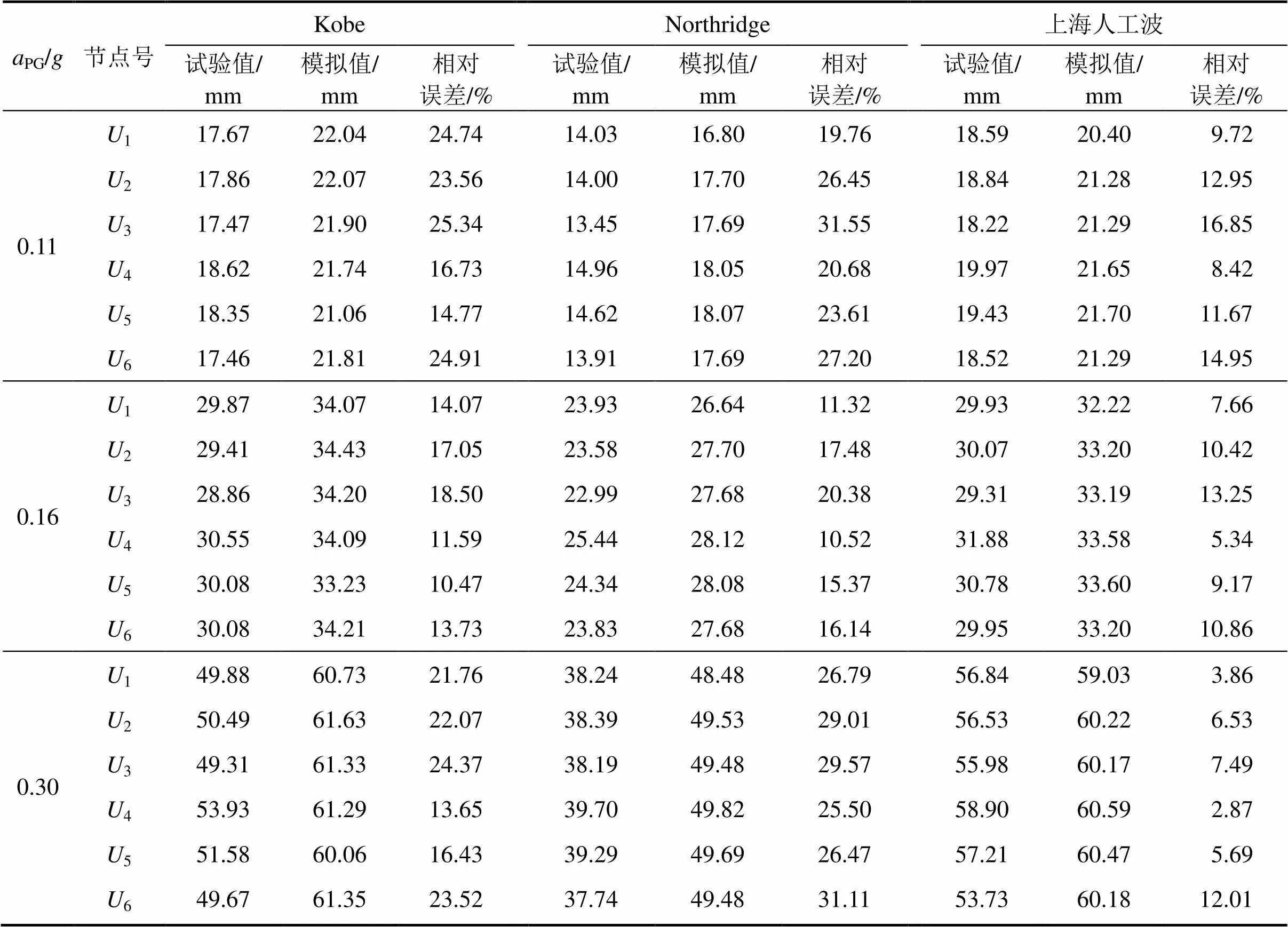
表6 网壳节点位移最大值的试验值与模拟值对比

对比分析表6和图5可以看出：

1) 在Kobe波和Northridge波作用下，网壳节点位移最大值的试验值与模拟值的误差基本维持在25%之内；在上海人工波作用下二者的误差基本在15%之内，吻合度更好。这种现象是由于相互作用体系与地震波主频一致发生共振，使得网壳地震响应增大，节点位移响应剧烈使得试验值偏大，致使误差减小。

2) 在不同地震波下网壳节点的位移时程曲线试验结果与模拟结果的波形和相位基本吻合，呈现出一致的变化规律。

3) 不同地震波作用下网壳节点位移存在差异，这是由不同地震波的频谱特性所引起。

3.4 网壳杆件应变响应

为研究不同地震波作用下土−独立基础−单层柱面网壳结构杆件应变响应规律，表7所示是PG为0.11，0.16和0.30地震作用下网壳杆件2，8，10和11杆件应变峰值的试验值与模拟值。图6所示是PG为0.11时杆件11应变时程曲线的试验结果与模拟结果的对比。

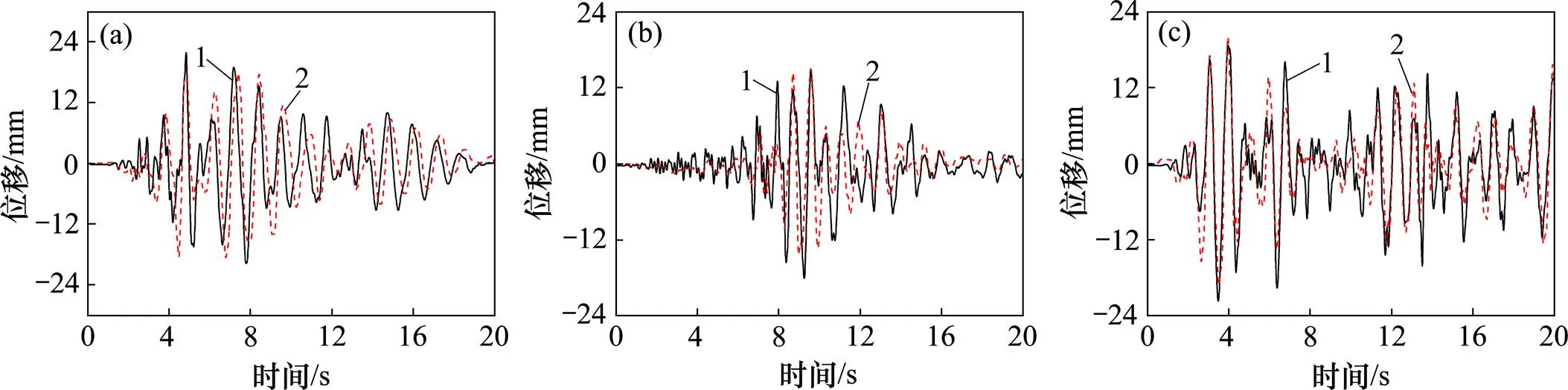
(a) Kobe；(b) Northridge；(c) 上海人工波

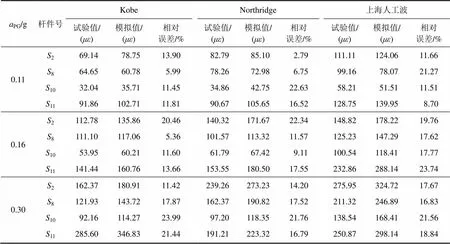
表7 不同杆件应变试验最大值与模拟最大值对比

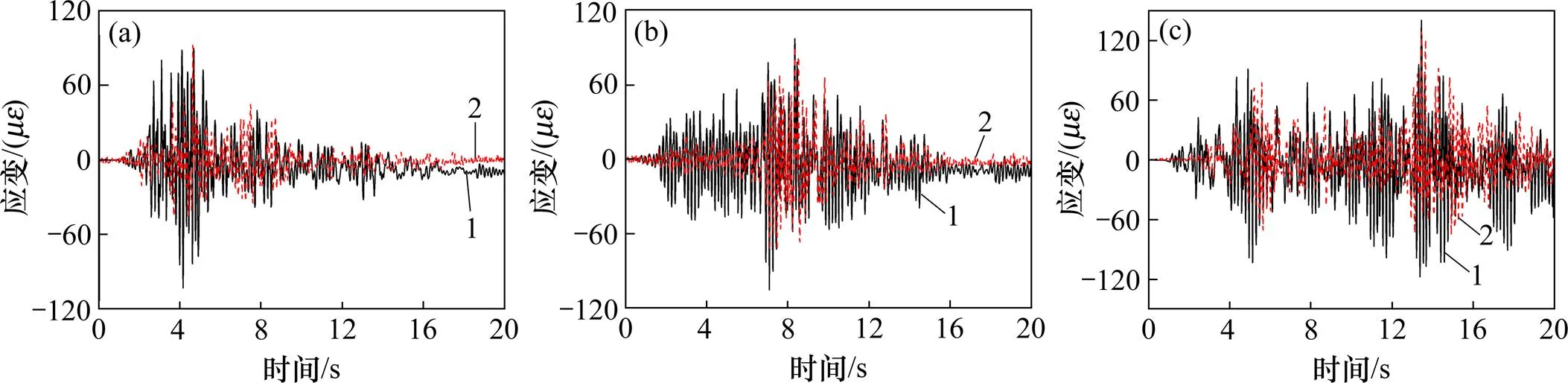
(a) Kobe；(b) Northridge；(c) 上海人工波

对比分析表7和图6可以看出：

1) 在不同工况下，网壳相同杆件应变最大值的试验值与模拟值的最大相对误差基本在20%之内，随着输入地震波强度的增大误差增大。这是由于随着振动次数的增多，试验中的土体与基础之间产生了较大的缝隙，使得土体与基础产生了滑移和提离现象，从而致使响应误差增大。

2) 在不同地震波作用下，网壳杆件应变时程曲线的试验结果与模拟结果的波形和相位基本吻合。

3) 在不同地震波作用下，网壳杆件应变最大值存在差异，这是不同地震波的频谱特性差异所致。

4 误差分析

理想状态下有限元数值模拟结果与试验结果的相对误差最大值基本在20%左右，少数误差偏大。分析认为主要有以下几个因素引起。

1) 振动台局部非一致现象。对试验采集的4个子台台面的加速度时程曲线数据处理中发现，4个子台采集到的加速度峰值存在差异，这是锚固4个子台的地锚在振动过程中发生不同程度的松动以及控制4个子台的12根作动器之间存在局部非一致运动导致的。试验油压的不稳定也会使得台面存在局部非一致性，使试验结果偏小。

2) 模型箱效应。通过对试验模型的数值模拟发现，数值模拟中采用的理想黏弹性边界条件与试验采用的刚性箱在边界刚度上存在一定的差异。数值模拟中采用的是模拟无限地基土域的理想黏弹性边界，试验中采用的箱体虽通过增大塑料泡沫厚度、施加软橡胶皮等措施减小模型箱效应，仍不能完全保证与无限地基土域的一致。

3) 基础与土体的非线性接触。试验过程中观察到土体与基础之间存在明显的提离和滑移现象，使得二者之间的约束变弱，即二者之间的摩擦因数减小，而数值模拟中采用理想状态下的面面接触模拟。

4) 土体参数测定误差。试验土体的力学参数虽采用土体分层夯实后现场取样测定，取了多个测点求取平均值，但在测定土体参数的过程中发现测得结果存在离散性，虽采用直剪法和动三轴试验进行了对比测试，但与实际情况仍存在一定的差距。此外，由于试验模型箱很大，采用了15 m3土体，不可能做到每次振动重新填土夯实或重新测量参数，多次振动后土体的密实度也会发生变化。

5) 试验采集误差。试验在采集加速度和位移时分别采用压电式传感器和拉线位移计。对压电式传感器而言，由于试验周期较长，在测量土体加速度时，为防止水分渗入传感器内，采用气球、防水胶布、干燥剂等对传感器进行防水处理，在固定上部网壳测点传感器时采用的橡皮泥，影响加速度数据采集精度，使得试验值偏小。拉线位移计固定在临时搭制的脚手架上，在振动过程中由于台面振动、外界扰动、土体的沉降等都会使得拉线位移计的拉线偏离水平位置，使测量产生误差。

6) 不可避免的人为仪器安装误差、试验过程中有其他试验的进行导致油压不稳定等外界干扰因素，都是导致误差产生的原因。

5 结论

1) 考虑土−结构相互作用下，土−独立基础−单层柱面网壳结构体系的试验结果与模拟结果变化规律基本吻合，互相验证了试验和模拟方法的正确性。

2) 土−结构相互作用下基础底部的加速度峰值响应较自由场加速度峰值响应增大，增大5%~30%，这不利于结构的抗震设计。

3) 土体与基础之间滑移和提离现象及模型箱的刚度是影响试验结果与模拟结果差距的主要因素，尤其是随着振动次数的增多，土体与基础之间的非线性接触是影响试验精度的关键因素。

4) 地震波频谱特性是影响土−独立基础−单层柱面网壳结构地震响应的重要因素，在试验设计时应当尽量避开结构体系与地震波主频一致而发生共振，否则试验结果可能失真。

；

[1] 蓝天, 张毅刚. 大跨度屋盖结构抗震设计[M]. 北京: 中国建筑工业出版社, 2002: 27−33. LAN Tian, ZHANG Yigang. Seismic design of long-span roof structure[M]. Beijing: China Architecture & Building Press, 2002: 27−33.

[2] 石光磊, 甘明. 薛素铎. 网架结构支座周边杆件抗震设计研究[C]// 第十四届空间结构学术会议. 福州, 2012: 242−245. SHI Guanglei, GAN Ming, XUE Suduo. The bearing peripheral rods seismic design of grid structure[C]// Proceedings of the Fourteenth Symposium on Spatial Structure. Fuzhou, 2012: 242−245.

[3] 曹资, 张超, 张毅刚, 等. 网壳屋盖与下部支承结构动力相互作用研究[J]. 空间结构, 2001, 7(2): 19−26. CAO Zi, ZHANG Chao, ZHANG Yigang, et al. Dynamic interaction study between net shell roof and support structure[J]. Spatial Structure, 2001, 7(2): 19−26.

[4] 曹资, 薛素铎, 冯远, 等. 张弦网壳结构地震响应规律分析[J]. 钢结构, 2011(4): 1−5. CAO Zi, XUE Suduo, FENG Yuan, et al. Seismic response analysis of latticed shell with tension chord[J]. Steel Construction, 2011(4): 1−5.

[5] 支旭东, 于志伟, 范峰. 下部支承结构对网壳结构强响应的影响研究[J]. 建筑钢结构进展, 2012, 14(4): 27−31. ZHI Xudong, YU Zhiwei, FAN Feng. Influence study of substructure upon dynamic response of reticulated shells under severe earthquakes[J]. Progress in Steel Building Structures, 2012, 14(4): 27−31.

[6] TSKEUCHI T, OGAWA T, KUMAGAI T. Seismic response evaluation of lattice shell roofs using amplification factors [J]. Journal of the International Association for Shell and Spatial Structures, 2007, 48(3): 197−210.

[7] NAOKI S, KENICHI S. Damping evaluation using full-scale date of building in Japan[J]. Journal of Structural Engineering, 2003, 129(4): 470−477.

[8] YANG Dabin, ZHANG Yigang, WU Jinzhi. Computation of Rayleigh damping coefficients in seismic time-history analysis of spatial structures[J]. Journal of International Association for Shell and Spatial Structures, 2010, 51(2): 125−136.

[9] 薛素铎, 孙艳坤, 栾小兵, 等. 考虑土−基础−结构相互作用的网架结构地震响应分析[J]. 建筑结构学报, 2010(S2): 34−38. XUE Suduo, SUN Yankun, LUAN Xiaobing, et al. Seismic response analysis of space grid structure considering soil-foundation structure interaction[J]. Journal of Building Structure, 2010(S2) 34−38.

[10] 王国华, 薛素铎, 李雄彦, 等. 考虑土−结构相互作用的单层球面网壳动力稳定性研究[J]. 工业建筑, 2011(S2): 499−506. WANG Guohua, XUE Suduo, LI Xiongyan, et al, Stability analysis of single-layer spherical reticulated considering soil-structure interaction[J]. Industrial Construction, 2011(S2): 499−506.

[11] LUAN Xiaobing, XUE Suduo. The effect of soil structure interaction on the seismic response of spatial structure subjected to the near fault excitation[J]. Applied Mechanics and Materials, 2011, 94/95/96: 877−882.

[12] 楼梦麟, 邸龙. 考虑土−结构相互作用双层柱面网壳在多点输入下的地震反应[J]. 地震工程与工程振动, 2006, 26(3): 228−231. LOU Menglin, DI Long. Seismic response analysis of double-layer cylindrical reticulated shell under multiple support excitations considering dynamic soil-structure interaction[J]. Earthquake Engineering and Engineering Vibration, 2006, 26(3): 228−231.

[13] 唐敢, 陈少林, 王法武, 等. 空间结构−地基动力相互作用的三维时域数值分析方法[J]. 工程力学, 2009, 26(8): 143−149. TANG Gan, CHEN Shaolin, WANG Fawu, et al. Three-dimensional numerical analytical method in time domain for soil-spatial structure dynamic interaction[J]. Engineering Mechanics, 2009, 26(8): 143−149.

[14] 刘毅, 薛素铎, 李雄彦, 等. 土−结构动力相互作用下网架结构简化分析方法研究[J]. 振动与冲击, 2015, 34(11): 75−82. LIU Yi, XUE Suduo, LI Xiongyan, et al. Simplified analysis method of grid structure considering soil-structure dynamic interaction[J]. Journal of Vibration and Shock, 2015, 34(11): 23−30.

[15] 薛素铎, 刘毅, 李雄彦. 协同工作条件下地基土对单层球面网壳结构动力性能的影响[J]. 工程力学, 2014, 31(9): 133−141. XUE Suduo, LIU Yi, LI Xiongyan. Analysis of foundation soil effect on dynamic performance of single-layer spherical latticed shell under cooperative work[J]. Engineering Mechanics, 2014, 31(9): 133−141.

[16] 刘毅, 薛素铎, 李雄彦. 土−结构动力相互作用下网架结构动力性能研究[J]. 振动与冲击, 2014, 33(10): 23−30. LIU Yi, XUE Suduo, LI Xiongyan. An analysis of grid structure dynamic performance considering soil-structure dynamic interaction[J]. Journal of Vibration and Shock, 2014, 33(10): 23−30.

[17] XUE Suduo, LIU Yi, LI Xiongyan. Dynamic performances analysis of single-layer cylindrical reticulated shell considering pile-soil-structure interaction[J]. Journal of the International Association for Shell and Spatial Structures. 2015, 56(2): 91−100.

[18] 史晓军, 岳庆霞, 李杰. 土−结构动力相互作用振动台试验中模型地基影响因素分析[J]. 建筑科学与工程学报, 2007, 24(4): 50−53. SHI Xiaojun, YUE Qingxia, LI Jie. Influence factor analysis of foundation model in shaking table test considering soil- structure dynamic interaction[J]. Journal of Architecture and Civil Engineering, 2007, 24(4): 50−53.

[19] FIHMAN K L, MANDER J B, RICHARDS R. Laboratory study of seismic free-field response of sand[J]. Soil Dynamics and Earthquake Engineering, 1995, 14(1): 33−43.

[20] LIU Jingbo, LI Bin. A unified viscous-spring artificial boundary for 3-D Static and dynamic applications[J]. Engineering and Materials Science, 2005, 48(5): 570−584.

[21] 赵建峰, 杜俢力, 韩强, 等. 外源波动问题数值模拟的一种实现方式[J]. 工程力学, 2007, 24(4): 52−58. ZHAO Jianfeng, DU Xiuli, HAN Qiang, et al. An approach to numerical simulation for external source wave motion[J]. Engineering Mechanics, 2007, 24(4): 52−58.

(编辑 杨幼平)

Shaking table test of single-layer latticed cylindrical shell considering soil-structure interaction and its numerical analysis

LIU Yi1, 2, XUE Suduo2, WANG Guoxin2, LI Xiongyan2

(1. CRRC Construction ENGRG. Co. Ltd., Beijing 100078, China;2. College of Architecture and Civil Engineering, Beijing University of Technology, Beijing 100124, China)

The thesis mainly talks about a single-layer latticed cylindrical shell with 1.8 m in length and 1.8 m in span, and a shaking table test of soil-independent foundation-latticed cylindrical shell was realized based on a model box with 7.7 m in length, 3.2 m in width and 1.2 m in depth. Then, the seismic responses of soil-independent foundation-latticed cylindrical shell subjected to different earthquake waves were studied. At the same time, a finite element model of shaking table test was established, and the numerical simulation results were compared with the test results. The results show that the test results and numerical results are in good agreement, and the peak acceleration of foundation increase compared to the peak acceleration of free field. The sliding and separation phenomenon between soil and foundation is a principal factor to affect the error between test results and numerical results. The nonlinear relationship between soil and foundation become more apparent along with the increase in vibration frequency. The spectrum characteristic of different earthquake waves is also an important factor to affect the seismic response of soil-independent foundation-latticed cylindrical shell. The resonance phenomenon should be paid more attention to between structure system and dominant frequency of earthquake wave to avoid the distortion of test results when a shaking table test is designed.

single-layer latticed cylindrical shell; soil-structure interaction; shaking table test; numerical simulation; seismic response

10.11817/j.issn.1672-7207.2017.01.030

TU311.3

A

1672−7207(2017)01−0223−10

2016−01−24；

2016−04−06

国家自然科学基金资助项目(51078010, 51278008)；北京市自然科学基金资助项目(8112005) (Projects(51078010, 51278008) supported by the National Natural Science Foundation of China; Project(8112005) supported by Beijing Municipal Natural Science Foundation)

刘毅，博士，工程师，从事大跨空间结构、地下空间结构抗震研究；E-mail: jiesenliu@sina.com