非等时距MGM（1，m）模型在高速公路沉降预测中的应用

罗 杰

（1.湖南有色测绘院有限公司，湖南 长沙410129）

非等时距MGM（1，m）模型在高速公路沉降预测中的应用

罗 杰1

（1.湖南有色测绘院有限公司，湖南 长沙410129）

分别以Lagrange插值法和三次样条曲线法为基础，利用灰色理论建立高速公路沉降预测的非等时距GM（1，m）模型。分析比较MGM（1，m）与GM（1，1）模型精度，基于非等时距的MGM（1，3）模型沉降预测结果与实测情况吻合较好，拟合与预测精度也比非等时距GM（1，1）的精度高，非等时距的序列转换采用Lagrange插值函数法和三次样条曲线法求得，对于此次工程数据采用三次样条曲线法较Lagrange插值函数法精度高。

高速公路，沉降变形，多变量灰色模型，非等时距

由于地质勘察、室内试验、土工计算方法存在误差，同时，实际的地基处理和路基施工进度也与设计的预期安排有所不同，现场发生的沉降量及其过程与初始设计往往存在很大的差异，因此，需要通过分析现场实测沉降资料来预测后期沉降量，必要时还须校核、修改、补充设计，在施工过程中对路基沉降变形进行动态设计和施工控制。工程上大多采用部分实测沉降数据来推算沉降量，主要方法有经验公式法、三点法、Asao-ka法、灰色系统法、遗传算法和神经网络法等[1-3]。本文对灰色系统法在沉降预测中的应用进行了分析。

高速公路的变形监测不能只对单点（或单方向）进行局部分析研究，应该充分利用监测点之间的相关信息。本文应用多变量灰色模型（multi-variable grey model，MGM（1，m）模型），从系统的角度对多变量进行统一描述，能较好地反映系统中各变量之间相互影响的关系，进行建模并预测。MGM（1，m）模型是单点GM（1，1）模型在多点情况下的扩展，而不是GM（1，1）的简单组合，也不同于GM（1，m）模型。该模型不仅能够较真实地反映普遍联系的客观实际，而且拟合精度较高[2]。通过对非等时距序列的等时距化处理，可以拓宽该模型的使用范围，使之成为路基沉降预测的有效方法之一。

本文探索了灰色系统理论在沉降预测中的应用。针对工程实践中沉降观测资料一般都是不等时间间隔的特点[5-6]，采用Lagrange 插值法和三次样条曲线法对数据序列进行等时距变换。对不等时距沉降数据建立多变量灰色模型MGM（1，m）进行预测，并且与GM（1，1）模型的预测精度进行比较，结果表明MGM（1，m）与实际沉降量更接近，精度更高。

1 关联MGM（1，m）数学模型

MGM（1，m）模型的m个参数向量的最小二乘估计为：

当n=1时，MGM（1，n）退化为单一因子或单点序列的GM（1，1）模型。GM（1，n）模型适合于建立系统的状态模型、各变量动态关系分析以及为高阶建模提供基础，但不太适合于预测，MGM（1，n）模型既可以建模又可以预测。

2 应用实例

2.1 数据介绍

本文利用某高速公路某标段沉降观测成果验证上述模型与方法的实用性。后期连续非等间距（180 d）数据13组见表1。

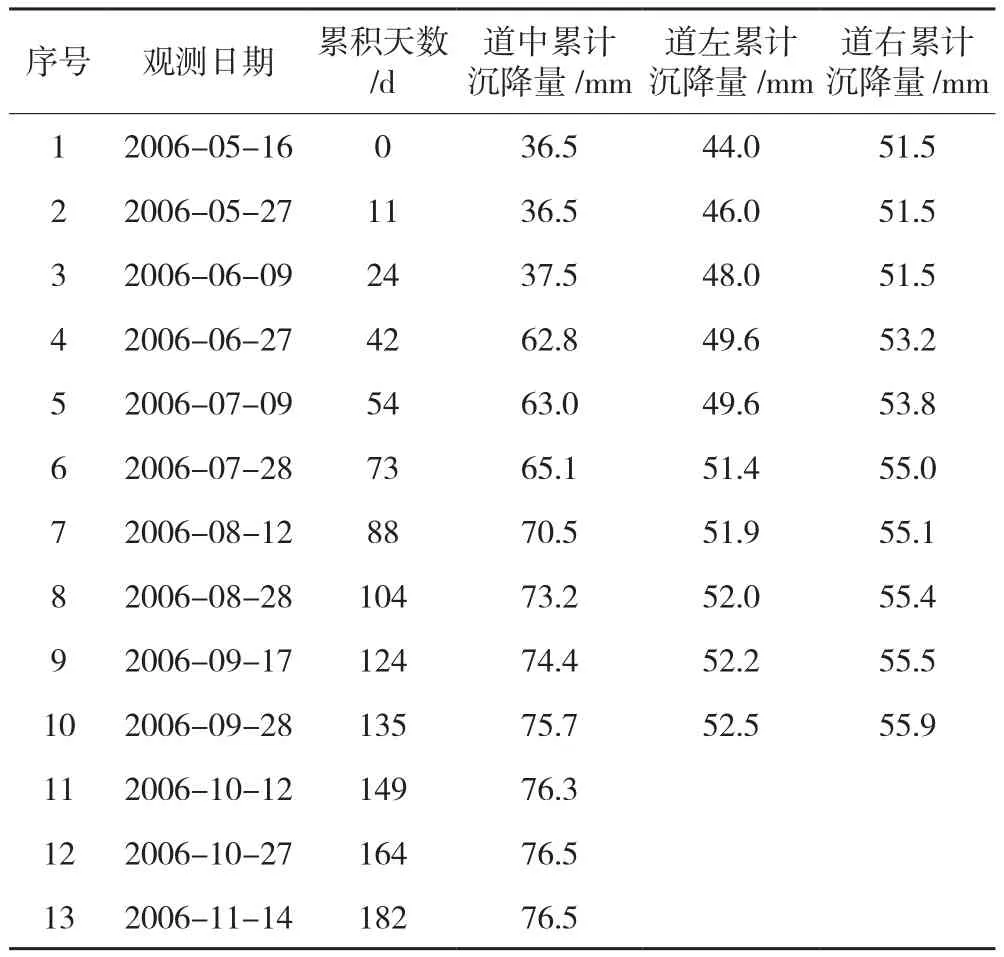
表1 某高速公路某标段沉降实测值

表中前十组数据用来建模，后三组用来检验预测精度。首先取道中、道左、道右3个变量，分别用x1、x2、x3表示，以此建立MGM（1，3）模型。

2.2 非等时距时间序列的等时距变换

非等时距时间序列的等时距变换方法有非等时距数列按等时距处理法、内插法（直线插值、Lagrange，牛顿插值）、样条曲线法等[4]。本文通过Matlab计算，分别采用Lagrange 插值法和三次样条曲线法对道中、道左、道右沉降量序列进行等时距变换得到两组不同的建模数据。

2.3 建立模型概述

取等时间间距的1～10组数据，按式（3）建立MGM（1，3）模型，取表1中数据求得L与Y，进一步计算时间响应式，求得后，按照式（7）还原计算即可得拟合预测值。

2.4 模型检验

通过Matlab 计算出的模型计算值和实测值，得到残差向量，即

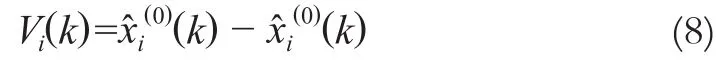
其中Vi=（Vi(1),Vi(2),…,n；k=1,2,…）。

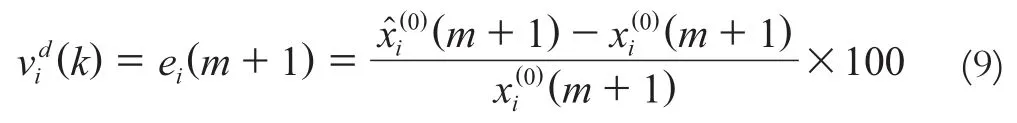
具体计算结果见表2和表3。

基于Lagrange插值法的MGM（1，3）模型中道中、道左、道右的平均绝对误差分别为2.5 mm、0.26 mm、0.176 mm，平均相对误差分别为4.41%、0.51%、0.327%；基于三次样条曲线法的MGM（1，3）模型中道中、道左、道右的平均误差分别为2.213 mm、0.225 mm、0.209 mm，平均相对误差分别为4.02%、0.49%、0.39%。这说明对于本工程数据采用三次样条曲线法较Lagrange插值函数法精度高。通过计算可得：基于Lagrange插值法的MGM（1，3）模型的C=0.240 3、P=1，精度等级好；基于三次样条法的MGM（1，3）模型的C=0.230 4、P=1，精度等级也好；GM（1，1）模型的C=0.484 6、P= 0.777 8，精度等级勉强可以。

2.5 MGM（1，3）与GM（1，1）预测模型的比较

对于道中沉降，分别比较MGM（1，3）与GM（1，1）预测模型的拟合、预测精度，三种模型的比较见图1，道中沉降预测结果见表4。这个结论对于其他类型工程是否合理，还有待进一步验证。

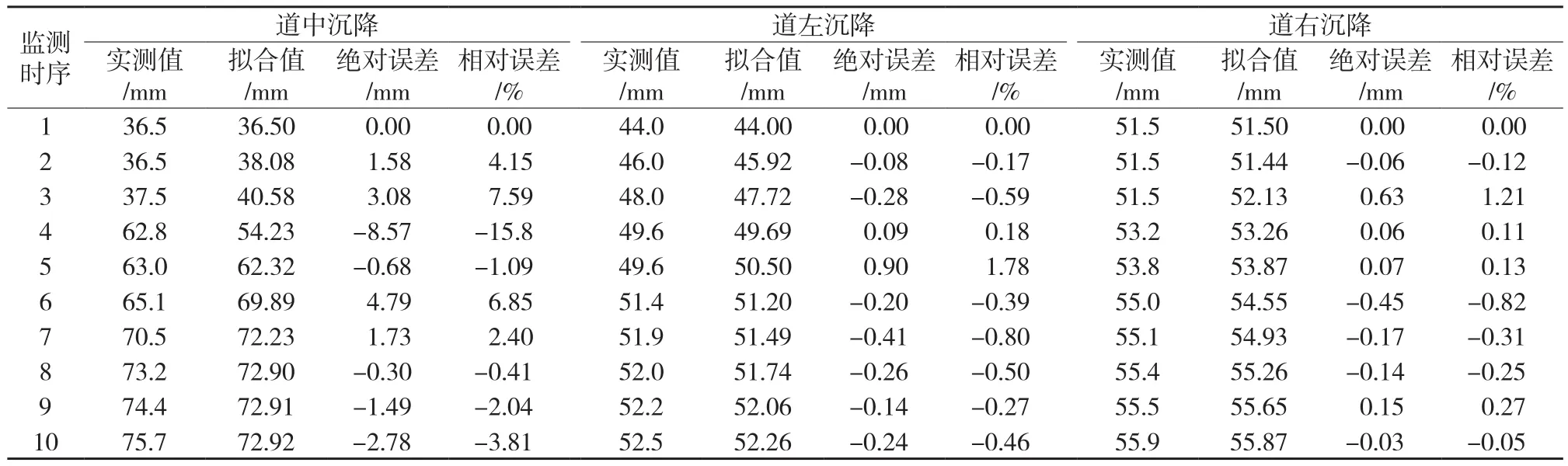
表2 基于Lagrange插值法的MGM（1，3）模型逐点残差

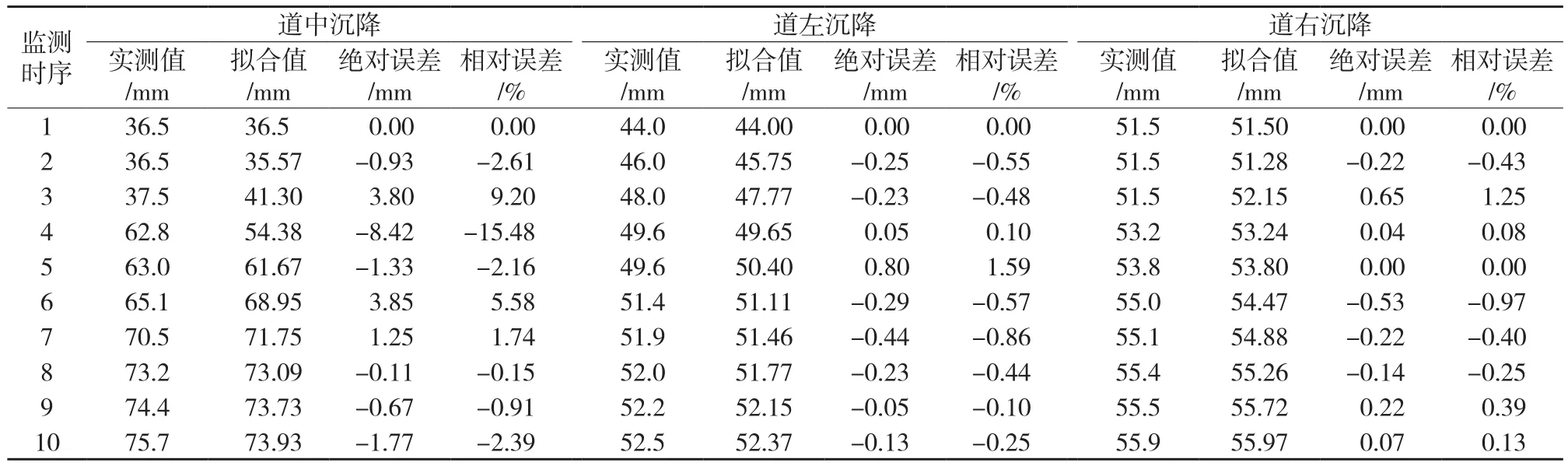
表3 基于三次样条法的MGM（1，3）模型逐点残差

表4 道中沉降预测结果

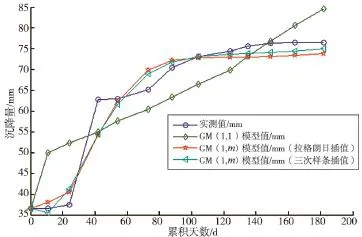
图1 三种模型拟合及沉降预测值曲线

3 结 语

通过对非等时距多变量灰色模型的介绍及其在某高速公路某标段沉降工程实例中的应用，可以得出如下结论：①基于非等时距的MGM（1，3）模型沉降预测结果与实测情况吻合很好，拟合与预测精度也较比非等时距GM（1，1）模型高。说明多变量预报模型MGM（1，m）对该类路面沉降预测是可行的。②非等时距的序列转换采用Lagrange插值函数法和三次样条曲线法求得，对于本工程数据，采用三次样条曲线法较Lagrange插值函数法精度高。

[1] 何习平,华锡生,田林亚.基坑开挖引起的建筑物沉降多点灰色预测模型[J].路基工程,2007(4):6-7

[2] 熊萍萍,党耀国,束慧.MGM（1，n）模型的特性研究[J].控制与决策,2012(3):389-393

[3] 孙小三,孙志久,范庆,MGM（1，m）模型在软土路基沉降沉降预测中的应用 [J].中南公路工程,2005(9):145-147

[4] 马保国,成国庆.一种相似关联度公式[J].系统工程理论与实践,2000(7):69-71

[5] 黄侃.基于自适应灰色模型的高速公路路基[J].交通标准化,2010(4):83-85

[6] 汪祖民,余祖英,杨晓晶.高速公路软土地基路堤沉降关联分析与预报[J].苏州科技学院学报,2007(9):41-47

[7] 彭府华,李庶林,李小强,等.金川二矿区大体积充填体变形机制与变形监测研究[J].岩石力学与工程学报,2015(1):104-113

P258

B

1672-4623（2017）02-0108-03

10.3969/j.issn.1672-4623.2017.02.033

2015-06-24。

罗杰，工程师，主要从事测绘工作。