抛物线拱结构的内力计算

张 宇 颂

(武汉外国语学校，湖北 武汉 430000)

抛物线拱结构的内力计算

张 宇 颂

(武汉外国语学校，湖北 武汉 430000)

介绍了抛物线拱结构的特点，以某对称的单跨两铰拱为例，采用精确计算法与简化计算法，计算分析了该拱结构的内力，并探讨了两种计算方法的优劣势和适用范围，为抛物线拱结构内力计算方法的选择提供参考。

拱结构，抛物线，结构力学，计算方法

抛物线具有优良的力学性能，工程实际中的拱结构很多就是采用抛物线形。采用抛物线形的拱结构内部几乎不承受拉力，可以充分发挥材料的力学性能。常用的抛物线拱桥为超静定结构，其内力计算往往是工程应用中的难点。查阅相关资料，其内力计算通常有两种方法：精确方法和简化方法。在相关力学资料中推导出了精确计算方法的公式，但由于计算比较困难，一般对一些参数采用近似假设后，给出了简化计算的例子。本文以一对称的单跨两铰拱为例，来讨论以上两种方法的具体实施过程，并对各自的优劣以及计算精度进行了对比。

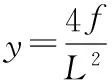
1 精确计算方法

用力法计算如图1所示的无拉杆两铰拱。由于是一次超静定结构，因此取简支曲梁为基本体系，如图2所示。

按基本体系在X1处沿其方向上在荷载及多余力的共同作用下，其位移应与原结构相同的位移条件建立力法典型方程如下：

δ11X1+Δ1P=0

(1)

计算系数与自由项，在X1=1作用下，曲梁的受力性能与拱相同，因此计算系数δ11时，应考虑弯矩和轴力的影响，计算公式如下：

(2)

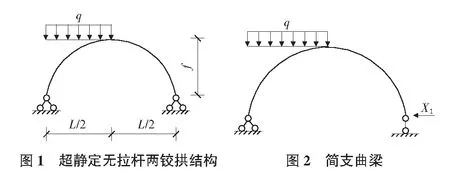
由图3可见：

(3)

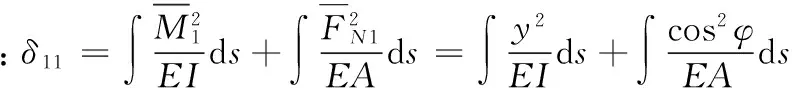
(4)

在FP作用下，曲梁的受力性能与简支梁相同，因此计算自由项Δ1P时，只需考虑弯矩的影响，计算公式如下：

(5)

同理：

(6)

因此：

(7)

由力法方程得到求无拉杆两铰拱多余未知力(即水平推力)的公式如下：

(8)

水平推力FH=X1求得后，各截面内力计算与静定三铰拱内力计算相同，公式如下：

(9)

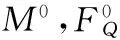
上述方法可以得到两铰拱较为精确的解，称之为精确解法。但由于计算十分复杂，不便于手算，所以在结构力学教材中一般没有给出具体计算的例题。下面就用精确解法对如图1所示两铰拱进行计算。

首先需要对式(8)中的ds，cosφ作进一步地推导：

由于：

(10)

(11)

所以δ11可写成：

(12)

其次计算Δ1P时，要先求出MP，可以利用如图4所示简支梁进行求解。弯矩MP的方程为：

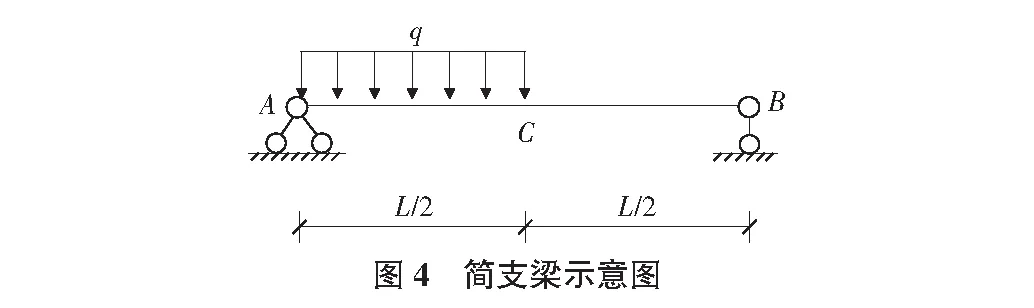
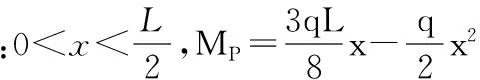
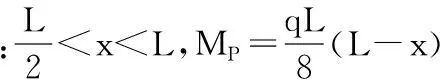
将MP代入后，Δ1P的计算式为：

(13)

将上述δ11，Δ1P代入式(8)就可以计算水平推力了。将本例相应简支梁的弯矩和剪力代入式(2)后，计算该两铰拱轴力和弯矩的具体计算公式如下：

对于左半跨(见图5)：

(14)

对于右半跨(见图6)：

FN=FBysinφ-FHcosφ

M=FBy(L-x)-FHy

(15)

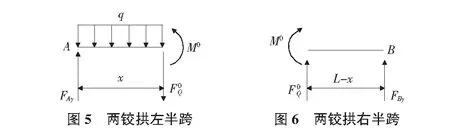
在δ11,Δ1P的计算式中存在积分计算问题，本文首先利用MATLAB对以上两式进行数值积分，先在MATLAB中建立关于δ11,Δ1P的被积函数，再调用MATLAB自带的牛顿—柯斯特积分函数qudal，求出δ11,Δ1P以及支座水平推力FH。然后再对式(14)，式(15)通过编程，求出x=3 m处的轴力FN3和弯矩M3、拱顶处的轴力FN7和弯矩M7以及x=11 m处的轴力FN11和弯矩M11，列于表1中。拱轴线的矢跨比分别取0.1，0.2，0.3，0.4，0.5。

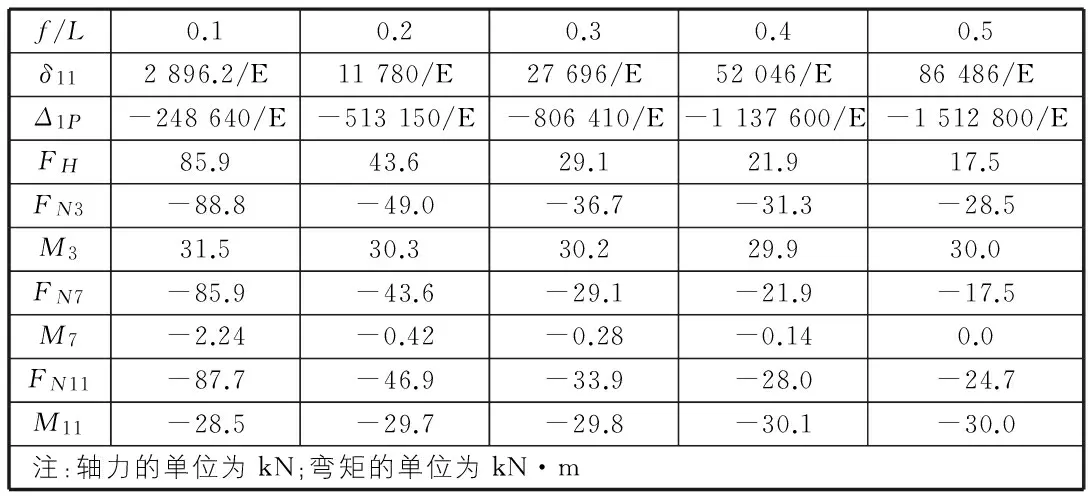
表1 抛物线拱结构精确计算结果表

以上主要介绍了精确法计算式(8)中“ds”“cosφ”的具体处理方法，以及如何借助相关软件用数值积分法解决式(8)中的积分问题。同时由表1的计算结果可以看到：在半边均布荷载作用下，随着两铰拱矢跨比的增大，轴力明显减小；在同一矢跨比下，轴力沿拱圈变化较小，基本上是个常数；同一点的弯矩，随拱矢跨比的改变而变化的幅度并不大。

2 简化计算方法

在一般的结构力学教材中都介绍了一种简化计算方法，它是基于以下两个简化假设的：

1)忽略拱的轴向变形，只考虑其弯曲变形；

经简化后力法方程中的系数和自由项的计算公式为：

(16)

下面用式(16)对如图1所示两铰拱再进行计算，且对所有的矢跨比均近似取ds=dx，cosφ=1。

把拱轴线方程y代入式(16)后，δ11的具体计算式如下：

(17)

把拱轴线方程y及MP的方程(同精确法)代入后，Δ1P的具体计算式如下：

(18)

把δ11和Δ1P代入力法方程，可求得水平推力FH的计算公式如下:

(19)

求出FH后同样可利用式(9)，通过编程求出x=3 m处的轴力FN3和弯矩M3、拱顶处的轴力FN7和弯矩M7以及x=11 m处的轴力FN11和弯矩M11，列于表2。

表2 抛物线拱结构简化计算结果表

由表2简化计算得到的结果可以看出：轴力的计算结果精度较高；同一点的弯矩与矢跨比的变化无关，是个常值；弯矩的误差相比轴力要大，而且矢跨比越小，误差越大。因此当拱的矢跨比小于0.1时，再使用简化方法，其计算结果的精度将得不到保证。

3 结语

通过以上的讨论可得出以下结论：

1)力学资料中介绍的精确法，计算十分复杂，手算几乎没有可能,虽然其中的积分运算部分可以通过相关软件解决。

2)力学资料中介绍的简化计算方法，可以解决简单拱结构的计算问题，也可以得到较为精确的结果，并满足学生练习的需要。

[1] 龙驭球.结构力学(上册)[M].北京：高等教育出版社，2000.

[2] 李 黎.结构力学[M].武汉：华中科技大学出版社，2014.

[3] 刘 磊，许克宾.结构分析中的曲梁单元[J].北方交通大学学报，2002(8)：88-89.

[4] 康 婷，白应生，李 庆.超静定拱内力的简化计算[J].路基工程，2009(5)：79-80.

[5] 寿 光.结构力学基础知识(拱结构)[J].建筑工人，1985(10)：79-80.

Internal force calculation of the parabola arch structure

Zhang Yusong

(WuhanSchoolofForeignLanguage,Wuhan430000,China)

The paper introduces characteristics of parabola arch structure. Taking the symmetric single-span two-hinged arch as an example, applying accurate calculation methods and simple calculation method, it calculates and analyzes the internal force of the arch structure, and explores their merits and defects and application scope, which has provided some guidance for selecting internal force calculation method of parabola arch structure.

arch structure, parabola, structural mechanics, calculation method

1009-6825(2017)02-0065-03

2016-11-07

张宇颂(1999- )，男，在读学生

TU311.4

A