改进自适应对消算法在工业噪声处理中的应用*

茅正冲， 涂文辉

(江南大学 轻工过程先进控制教育部重点实验室，江苏 无锡 214122)

改进自适应对消算法在工业噪声处理中的应用*

茅正冲， 涂文辉

(江南大学 轻工过程先进控制教育部重点实验室，江苏 无锡 214122)

分析了工业环境噪声的特点，将自适应噪声对消算法应用到工业噪声的处理当中。在传统最小均方(LMS)算法及基于Lorentzian函数的变步长LMS算法的基础上进一步进行约束稳定性条件处理，提出了一种约束稳定性变步长LMS算法，并在Matlab平台上进行了仿真验证。结果表明:算法具有更快的收敛速度以及更小的稳态误差，并且能有效地降低梯度噪声对算法性能的影响。

自适应噪声对消； 最小均方； 约束稳定性

0 引 言

由于工业噪声的干扰，工业环境下的语音通信变得十分困难，与语音相关的识别系统的性能也会急剧下降。因此，寻找一种有效的噪声处理方法十分重要。由于工业环境的复杂性，噪声功率较大，频谱较宽，很难估计出噪声的特性，处理难度大。自适应滤波的优点是在没有任何有用信号以及噪声的先验知识条件下，通过前一时刻获得的滤波器参数自动调节当前的参数，适应不断变化的噪声和有用信号的特性，实现某种最优滤波。1960年，Widrow和Hoff提出了最小均方(least mean square，LMS)算法，LMS算法计算量小，结构简单，易于实现，在自适应信号处理领域得到广泛应用[1]。传统的定步长LMS算法中步长取值会影响算法的性能，减小步长可以减小稳态误差，但会降低收敛速度和跟踪能力，增大步长会有更好的收敛速度和跟踪性能，但稳态误差较大[2]。

本文在LMS算法的基础上进行了改进，并将其应用到自适应噪声对消系统中，实现了工业噪声的有效处理。

1 工业噪声的特点

工业环境下的噪声十分复杂，这是由其声源种类多样性造成的，有机械运转产生的，也有动力摩擦产生的，有点声源也有线性声源。图1是从实际工业环境中采集的噪声的时域以及频域图。

从图1中可以看到，工业噪声的频谱范围很广，覆盖了整个语音信号的频率范围。除了宽带噪声之外，还叠加有多个频率分量的有色噪声，这些噪声分量主要来自机器的周期性运转，它们能量高，重叠在有用语音信号频谱之中。此外，在图1所示噪声信号末尾阶段，可以看到噪声的幅度明显增大，功率增大，体现了工业噪声的不稳定性。

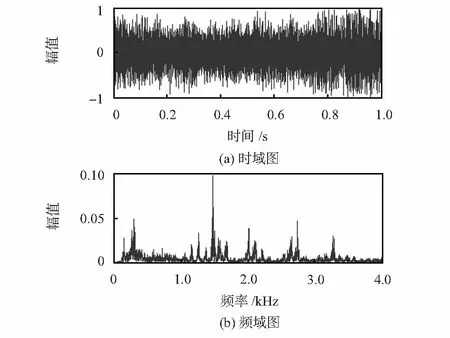
图1 工业噪声的时域及频域图

2 自适应噪声对消与LMS算法

2.1 自适应噪声对消系统

自适应噪声对消系统是自适应最优滤波器的一种变形[3]，它的基本原理如图2所示。自适应对消系统有两个输入端，主输入端和参考输入端。主输入端接收有用信号源发出的信号s和噪声源的噪声源产生的噪声信号v，s和v之间是不相关的。参考输入端接收噪声源产生的噪声信号x,由于v和x是由同一个噪声源产生的，它们之间存在某种相关性。利用参考噪声和主输入端中噪声的相关性，将参考噪声输入自适应滤波器，通过某种自适应算法对滤波器的参数进行调整，使得通过滤波器之后的参考噪声十分逼近有用信号中的噪声，最后通过减法器，就可以得到比较纯净的有用信号。

图2 自适应噪声对消系统原理

如图2所示，自适应对消系统的主输入通道的输入信号d=s+v，参考通道的输入为x，输出为y，整个系统的输出为

e=s+v-y

(1)

即有

e2=s2+(v-y)2+2s(v-y)

(2)

将上式两边同时取期望，可得到

E[e2]=E[s2]+E[v-y]2]+E[2s(v-y)]

(3)

由于有用信号s和噪声信号v，y均不相关，所以

E[e2]=E[s2]+E[(v-y)2]

(4)

所以

E[e2]min=E[s2]+E(v-y)2]min

(5)

当E[(v-y)2]达到最小值时，系统的输出e也达到最小值。最理想的情况下，v与x完全相关，此时y=v，e=s，完全消除了噪声的干扰。

2.2 基本LMS算法

LMS算法的基本思想是通过调整滤波器的参数，使得滤波器的输出信号与期望输出的信号之间有最小的均方误差[4]，这样系统输出为有用信号的最佳估计。基于最陡下降法的LMS算法的迭代公式为

e(n)=d(n)-XT(n)w(n)

(6)

w(n+1)=w(n)+2μe(n)X(n)

(7)

式中 X(n)=[x(n),x(n-1),…,x(n-N+1)]T，w(n)为n时刻输入时的滤波器权系数矢量，N为滤波器的阶数。μ为迭代步长，为了保证算法在迭代后能收敛，步长的取值范围是0<μ<1/λmax，λmax为输入信号自相关矩阵的最大特征值。在选择步长时，稳态误差和收敛速度之间是相互矛盾的，步长越小，稳态误差越小，收敛速度慢；步长越大，收敛速度快，收敛后的稳态误差也较大。

3 改进的变步长LMS算法

3.1 变步长LMS算法

为了解决稳态误差和收敛速度之间的矛盾问题，人们在基本LMS算法的基础上提出了许多变步长的LMS算法。文献[5～8]都是在LMS算法基础上进行的可变步长算法研究，这些算法的思路都是在迭代初始阶段，算法结果离最优解距离较远，采用较大的步长以加快算法的收敛速度，当离最优解距离较近时不断减小步长值来获得更小的稳态误差。

基于Sigmoid函数的变步长最小均方算法(SVSLMS)的步长更新公式为

μ(n)=β[1/(1+exp(-α|e(n)|))-0.5]

(8)

上述算法可以在脉冲信号持续期间内跟踪误差e(n)的变化起到步长调节的作用。但是这种表示的Sigmoid函数过于复杂，并且当误差e(n)接近于0时变化太大，不具有缓慢变化的特性，以至于在稳态阶段步长仍然有较大的波动。改进后的步长可以表示为

μ(n)=β[1-exp(-α|e(n)|2)]

(9)

式中β为参数控制步长的取值范围，α为参数控制函数的形状。改进后的函数更加简单，且当e(n)接近0时仍然能够缓慢变化。

文献[9]提出了一种基于Lorentzian函数的变步长LMS算法(LVSLMS)，其步长更新的表示为

μ(n)=αlg[1+0.5((e(n)/β)2]

(10)

式中α为控制步长取值范围，β为控制函数形状。该文献中已经论证此函数的性能优于Sigmoid函数，具有更快收敛速度和跟踪性能。

3.2 一种约束稳定性LVSLMS算法

将非线性应用到改变步长的函数中体现在归一化最小均方算法(NLMS)中，NLMS算法建立了步长因子和输入信号之间的非线性关系，在一定程度上解决了LMS算法收敛速度和稳态误差之间的矛盾，并降低了梯度噪声对系统输出误差的影响。但是NLMS算法没有考虑误差信号对步长因子的影响，同时NLMS算法的约束条件太过严苛，导致步长调整精度不高。NLMS算法的优化问题为

min‖δW(n+1)‖2

s.t. WH(n+1)X(n)=d(n)

(11)

式中δW(n+1)=W(n+1)-W(n)为权值增量，‖δW(n+1)‖2为欧氏范数平方运算。通过放宽对NLMS算法的条件，得到约束稳定性LMS算法，其算法的优化问题为

min‖δW(n+1)‖2

s.t.e[n+1](n)=e[n+1](n-1)

(12)

式中e[n+1](n)为用n+1时刻的权系数向量得到的n时刻的误差。式(12)表示在约束稳定性条件下权系数矢量增量的欧氏范数最小。文献[10]中通过引入拉格朗日乘子将带约束的最小化问题转换成不带约束的最小化问题，求解算法的优化问题，得到约束稳定性LMS算法的更新方程为

(13)

式中 ‖δX(n)‖2为输入矢量增量的范数的平方，δe[n](n)=e[n](n)-e[n](n-1)为前序误差增量，引入参数ε避免‖δX(n)‖2太小造成步长太大。本文在文献[9]提出的LVSLMS算法的基础上进行约束稳定性处理，得到一种约束稳定性LVSLMS算法，权系数矢量迭代公式可以表示为

(14)

式中μ(n)=αlg[1+0.5((e(n)/β)2]。

4 仿真结果与分析

为了验证本文算法的有效性，利用Matlab平台对本文中的算法进行了仿真实验。本次实验中的有用信号采用标准正弦波信号，干扰噪声信号来源于实际工业环境下的噪声录音，采样频率为8 kHz。

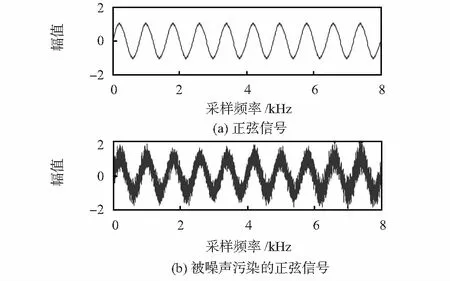
图3 正弦信号与加噪正弦信号

图3为加噪正弦信号，图4分别是固定步长LMS(FSLMS)算法、基于Sigmoid函数的可变步长LMS(SVSLMS)算法、基于Lorentzian函数的变步长LMS(LVSLMS)算法、以及本文算法的自适应噪声对消后的结果。其中,FSLMS算法中,步长u=0.04，SVSLMS算法中,β=0.1，α=0.5，LVSLMS算法中,α=0.2，β=0.8，本文算法中,α=0.6，β=0.5，ε=0.8，自适应滤波器的阶数为M=5。

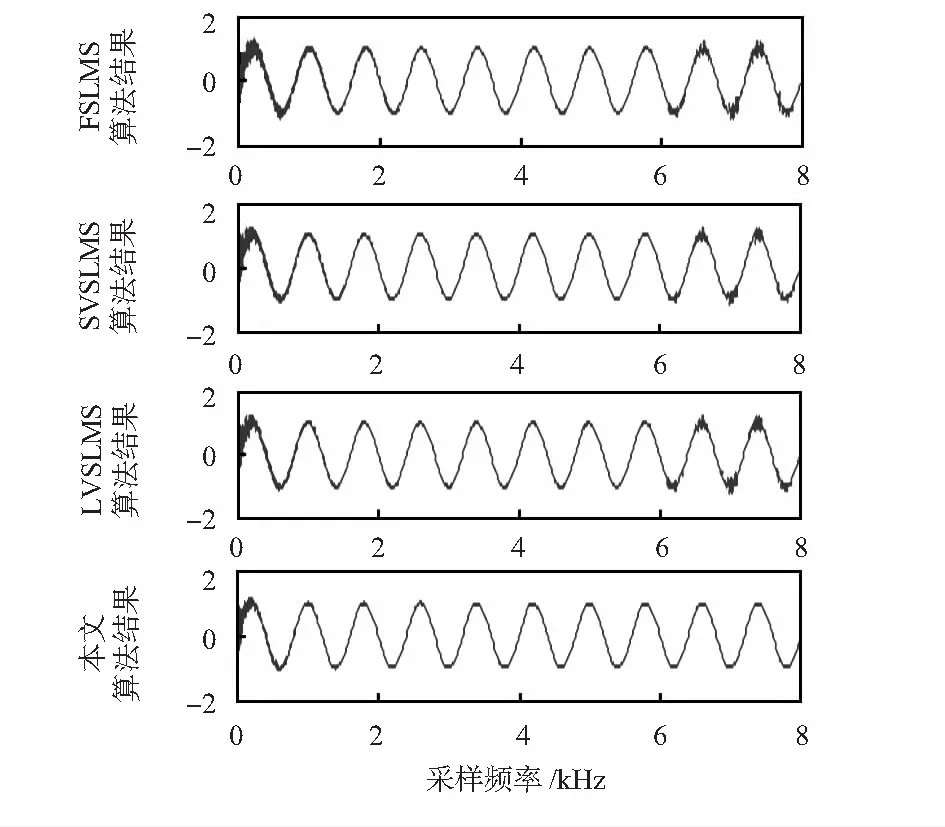
图4 不同算法处理的结果

从图4中可以看出，与固定步长LMS算法相比，后面三种算法收敛速度以及稳态误差方面都有了很大的改善，但是在输入信号的最后阶段，由于噪声的突然改变，噪声功率产生了改变，SVSLMS算法以及LVSLMS算法的误差突然会变得很大，这是由于滤波器权系数的收敛情况受噪声功率影响造成的。本文算法则不会受到噪声功率突变的影响，依然保持了很小的误差及追踪性能，降低了对梯度噪声的敏感性。表1是以上几种算法进行自适应噪声对消后的结果对比。

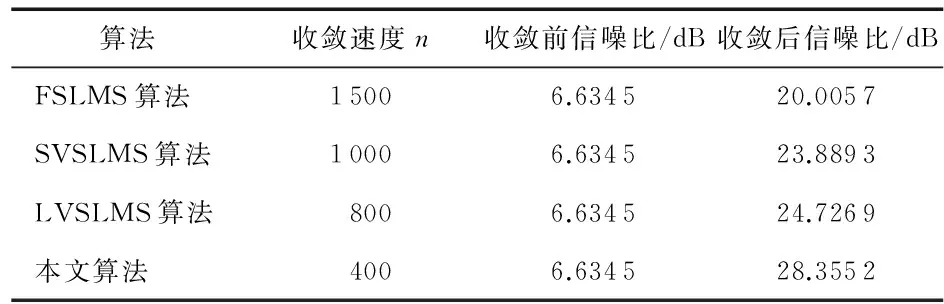
表1 四种算法处理结果对比

由表1可以看出，本文算法在收敛速度以及收敛后噪声的残留方面均有明显的优势。

5 结束语

针对工业噪声的复杂性，将自适应噪声对消应用到工业噪声的处理中是个不错的解决方法。由于传统的LMS算法存在缺陷，本文在变步长LMS算法的基础上作进一步的处理，使得LMS算法的收敛速度更快，稳态误差更小，能有效处理噪声功率的突发性变化。结果证明，本文算法能够有效地进行工业噪声的处理。

[1] 王海涛.自适应噪声对消在引信数字信号处理系统中的应用[J].制导与引信,2009(1):13-17.

[2] 贺洪江,王春霞.一种新的LMS自适应滤波算法分析仿真研究[J].传感器与微系统,2012,31(3):15-17，21.

[3] 李 红.一种变步长符号梯度脉冲噪声对消算法[J].重庆邮电大学学报：自然科学版,2014(5):654-658.

[4] 谭玉芳,杨 方.自适应噪声对消在抑制振动干扰中的应用[J].农业科技与装备,2010(2):44-46.

[5] Kwong R H，Johnston E W.A variable step size LMS algorith-m[J].IEEE Trans on Signal Processing,1992,40:1663-1642.

[6] 蒋明峰,郑小林,彭承琳.一种新的变步长LMS自适应算法及其在自适应噪声对消中的应用[J].信号处理,2001(3):282-286.

[7] 高 鹰,谢胜利.一种变步长LMS自适应滤波算法及分析[J].电子学报,2001(8):1094-1097.

[8] 覃景繁,欧阳景正.一种新的变步长LMS自适应滤波算法[J].数据采集与处理,1997(3):171-174.

[9] 刘剑锋,蒋卓勤,李 娟,等.一种基于Lorentzian函数的变步长LMS自适应滤波算法[J].指挥控制与仿真,2009(2):42-44.

[10] 张会芝,杨育捷,王鲜芳.一种约束稳定性最小均方波束形成算法[J].电光与控制,2014(3):33-37.

Application of improved adaptive noise cancellation algorithm in industrial noise processing*

MAO Zheng-chong， TU Wen-hui

(Key Laboratory of Advanced Process Control for Light Industry,Ministry of Education,Jiangnan University，Wuxi 214122，China)

The characteristics of industrial environmental noise is analyzed and the adaptive noise cancellation algorithm is applied to the processing of industrial noise.On the basis of traditional least mean square(LMS)algorithm and variable step size LMS algorithm based on Lorentzian function, the constraint stability condition is further processed.A variable step size LMS algorithm for constrained stability is proposed.In order to verify the effectiveness of the algorithm,simulation is carried out on the Matlab platform.And the result show that the proposed algorithm has faster convergence speed and smaller steady-state error.In addition,the influence of gradient noise on the performance of the algorithm is effectively reduced in this algorithm.

adaptive noise cancellation; least mean square(LMS); constraint stability

10.13873/J.1000—9787(2017)03—0157—04

2016—07—30

国家自然科学基金资助项目(60973095)；江苏省自然科学基金资助项目(BK20131107)

TN 912

A

1000—9787(2017)03—0157—04

茅正冲(1964-)，男，硕士，副教授，从事机器人视听觉识别，工业控制方向研究工作。