抑郁症静息脑电的小波包节点功率谱熵分析*
盖淑萍, 刘欣阳, 刘军涛, 孔 壮, 徐声伟, 蔡新霞
(1.中国科学院 电子学研究所 传感技术国家重点实验室(北方基地),北京 100190;2.中国科学院大学,北京 100190)
研究与探讨
抑郁症静息脑电的小波包节点功率谱熵分析*
盖淑萍1,2, 刘欣阳1,2, 刘军涛1,2, 孔 壮1,2, 徐声伟1,2, 蔡新霞1,2
(1.中国科学院 电子学研究所 传感技术国家重点实验室(北方基地),北京 100190;2.中国科学院大学,北京 100190)
头皮脑电(EEG)信号反映了大脑皮层神经元细胞群自发性节律性的电生理活动,含有丰富的生理与病理信息,是临床脑神经与精神疾病诊断的重要依据。针对抑郁症的研究和诊断中缺少客观有效的量化参数和指标的状况, 提出一种基于小波包分解节点重构信号的功率谱熵值(记为W值)的脑电信号分析方法,并利用此方法对静息态的脑电信号进行计算和分析。实验和分析结果表明: 抑郁症患者脑电信号S32节点(频率24~32 Hz)的熵值(置信区间[0.012 9,0.017 6])在部分脑区显著大于正常健康人(置信区间[0.024 6,0.030 3]),显示抑郁症病人快波节律的能量分布存在弥散性,符合现在关于抑郁症患者自我调节能力减弱的发病机制。对结果进行了T检验统计分析,证明了这种辨别方法的准确性和可行性,将为抑郁症疾病检测诊断提供有效的量化物理指标。
脑电; 小波包变换; 功率谱熵; 抑郁症; T检验
0 引 言
近年来,采用非线性动力学方法分析脑电(electroencephalography,EEG)信号, 给抑郁症的研究和诊断带来了新的研究思路和方法[1]。Ahmadlou M等人发现抑郁症患者β频段(15~30)整个额区(fractal dimension,FD)值均显著大于正常人[2]。通过计算脑电时间序列的熵值来衡量其复杂度的方法,反映了信号的不确定性和复杂程度[3]。然而传统的熵值计算方法(近似熵、小波熵),往往仅能考察整个序列或其谱能量分布的有序或无序程度,而欠缺对脑电信号某个特殊频段局部分布规律的详细研究。
小波包变换(wavelet packet transform,WPT)是在小波变换原理上推广而来的多尺度信号分析方法[4],已在故障诊断、肺音识别等方面得到了广泛的应用[5]。
本文引入一种分析脑电时间序列的新方法—小波包节点功率谱熵,运用该方法分别对抑郁症患者及正常对照组的脑电信号进行计算、处理和统计检验,并对实验结果进行了比较、分析和讨论,试图为抑郁症的病理诊断和疗效评估提供一种新的参考依据。
1 小波包节点功率谱熵的定义
小波包的基本思想是对多分辨率分析中的小波子空间进行分解[6]。3层小波包分解树,如图1所示。

图1 小波包分解树
对EEG信号f(t)进行小波包分解,提取小波包系数后,分别利用各系数进行小波包重构。f(t)经过小波包分解后,在第i分解层能够得到2i个子频带,所以,f(t)可以表示为

j=0,1,2,…,2i-1
(1)
式中 fi,j(ti,j)为小波包分解在第(i,j)层节点上的重构信号。
对长为L的子空间重构信号x(n)进行功率谱计算
(2)
(3)
式中 P(k)为信号的功率谱序列;XL(fk)为信号的离散傅里叶变换(DFT);fs为信号的采样频率。
熵定义为新信息的产生率,样本熵是由Richman提出的一种序列复杂性测度方法,参考样本熵的计算方法,将功率谱熵定义如下:
设功率谱序列为p(1), p(2),…, p(N),共N点。
1)按序号顺序连续成m维矢量
P(i)=[p(i),p(i+1),…,p(i+m-1) ],
i=1~N-m+1
(4)
2)定义P(i)与P(j)之间的距离d[P(i),P(j)]为两者对应元素中差值最大的一个。即
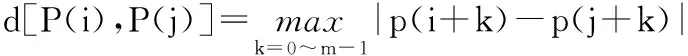
(5)
此时P(i)与P(j)中其他对应元素间差值自然都小于d[P(i),P(j)],并对每一个i值计算P(i)与其余矢量P(j),(j=1,2,…,N-m+1)的距离d[P(i),P(j)]。

(6)
(7)
5)功率谱序列的熵值为
En(m,r,N)=-ln[Bm+1(r)/Bm(r)]
(8)
式中 En(m,r,N)的值与参数m,r和N的取值有关,一般取m=1或2, r=0.1SD~0.25SD(SD是原始数据x(i)的标准偏差)时计算得到的功率谱熵值具有较为合理的统计特性,在本研究中选取参数m=2, r=0.2SD。
2 基于小波包节点功率谱熵的抑郁症诊断分析
2.1 研究对象
本实验的健康人和抑郁症患者志愿者由中国人民解放军海军总医院提供,相应研究通过了伦理审查。本次实验抑郁志愿者符合规定的入组标准,符合美国精神障碍诊断与统计手册第4版(diagnosticandstatisticalmanualofmentaldisorders,fourthedition,DSM-IV)诊断标准[7],被试者均为右利手。本研究分别采集了22位健康志愿者和22位抑郁症患者志愿者的脑电数据,男女各11名,年龄在20~55岁。
2.2 实验数据采集
利用NuAmps放大器(NeuroScan,USA)脑电测试仪,交流采样模式,采样频率为1kHz,分别对包括额叶、顶叶、颞叶、枕叶区域在内的19个位点Fp1,Fp2,F7,F3,Fz,F4,F8,T3,C3,Cz,C4,T4,T5,P3,Pz,P4,T6,O1,O2进行了EEG信号检测,位点选择符合脑电10~20系统(Jesper,1958)检测标准[8],测试脑电位点示意图如图2所示。测试中,选择两侧乳突(A1和A2)的电压平均值作为参考,同时采集了垂直眼电和水平眼电,以排除眼电对脑电采集的影响。测试环境选择避光安静的房间,被试者静坐,闭眼放松。采集被试者静息状态10minEEG信号,选取20 000长度数据进行分析,采用Matlab软件进行分析。
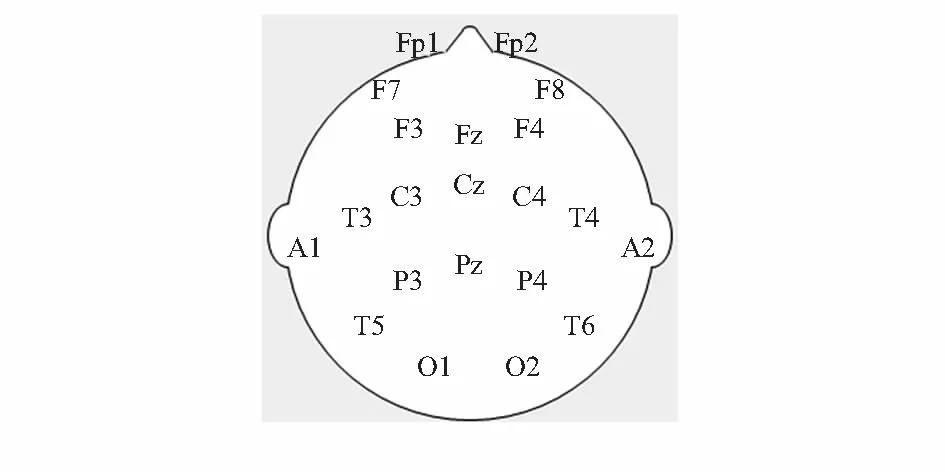
图2 脑电测试位点
2.3 分析方法
利用Curry 7软件去除采集得原始脑电信号中的眼电和坏区,进行 0.5~50 Hz的滤波处理,128 Hz降采样后得到脑电信号S。根据小波包分解算法,采用二进尺度变换,利用离散db4小波对S进行3层小波包分解,对各节点重构后做功率谱计算,得到各节点功率谱序列后,求各节点功率谱熵,得到W值,以考察脑电信号各频段功率值的分布规律,算法流程图如图3所示。

图3 脑电信号处理方法流程图


表1 各节点重构信号对应频率范围
根据头皮脑电的频段特征,脑电信号的频率主要集中在在0.5~30 Hz,可以看出S30,S31,S32和S33节点频谱位于0~32 Hz,涵盖了头皮脑电的频率范围,因此,可以分析这4个节点的小波包重构信号来研究各频率波段的功率谱熵特征。
3 实验结果与分析
3.1 两组被试不同频段W平均值对比分析
对抑郁症患者组和健康人对照组的实验数据进行分析。首先根据本文提出的方法计算每位被试者各个位点的值,然后计算22位被试者各位点S30,S31,S32和S33节点W值的平均值,得出各位点两组样本数据W值的差异。通过实验分析Fp1, Fp2, F3, F4, P3, P4位点的结果差异性最明显,因此,本文仅对这6个位点的分析结果进行详细讨论,分析结果如图4所示。

图4 小波包分解节点S30,S31,S32和S33功率谱熵的均值
3.2 两组被试各位点S32频段W值对比分析
通过分析图4,可以得知两组被试者的各位点的S32频段均有明显差异,本文进一步对Fp1, Fp2, F3, F4, P3, P4位点的各个被试者S32频段的W值进行了对比分析,如图5所示。分析图5中6通道脑电值与被试者脑功能整体状态的关系,可知抑郁症患者的W值明显高于正常人。
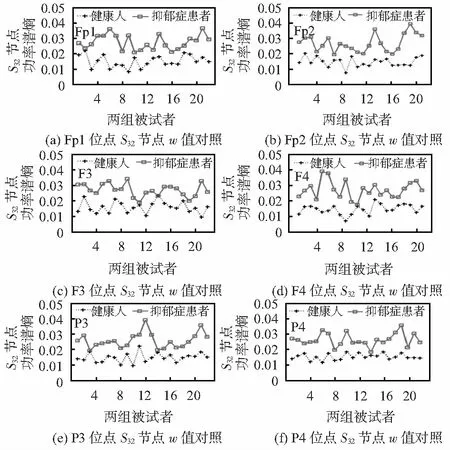
图5 健康人和抑郁症患者被试者S32节点W值的比较
3.3 统计分析与假设检验
对两组被试上述差异的显著性作统计检验,以验证算法的准确性和可行性。采用SPSS统计软件对结果进行T检验。主要方法如下:
1)分别将抑郁症患者和健康人对照组6个位点S32频段W值进行单样本T检验。以Fp1位点举例说明,结果如表2所示。
抑郁症患者组W值在显著性水平α取 0.01时的置信区间为[0.024 6,0.030 3],即将[0.024 6,0.030 3]作为郁症患者组W值判断区间时,误判概率小于0.01,Fp2,F3,F4,P3,P4位点单样本T检验得到的结果与Fp1一致。表明两组被试的静息态脑电信号确实存在差异,这种差异可以通过这6个位点S32节点的W值准确地进行分析和判断。
2)同样对抑郁症病人和健康人对照组Fp1位点W值的差异显著性进行假设检验,使用SPSS统计软件进行独立样本T检验,结果如表3所示。分析表3可以得到结论:在分别假设这两组脑电信号的值方差相等和不等两种情况下, 其差异显著性基本相同,均值差值均为0.012。这两组脑电信号W值差值在显著性水平α取0.01时,置信区间为[0.008 7,0.015 8],这表明抑郁症患者Fp1位点S32频段的W值显著大于健康对照组,Fp2,F3,F4,P3,P4位点得到的结果一致。这说明该分析方法可以有效地区分抑郁症患者和健康人的脑电信号,从而为抑郁症的临床诊断提供量化的可靠依据。

表2 单样本T检验分析结果

表3 独立样本T检验分析结果
3.4 结果讨论
实验和分析结果表明, 抑郁症患者Fp1,Fp2,F3,F4,P3,P4 位点静息态脑电信号小波包分解后S32节点的功率谱熵值显著大于健康对照组。熵值越大,表明信号的能量分布复杂度越高、越不规律。从神经科学知识可知,S32节点的频段包含在脑电节律β2(18~32 Hz) 中,而β2高频快波作为大脑皮层兴奋时的主要波形,其能量分布复杂度体现了大脑活动的规律程度。抑郁组S32频段W值大,表明其功率弥散性增加,说明安静闭目状态下抑郁症患者的脑电活动不如健康组规律,这也证明本文提出的小波包节点功率谱熵值可以作为衡量大脑自我调控能力的物理指标。
4 结 论
利用本文方法对抑郁症患者和健康人的脑电信号进行了计算、分析和讨论。得出抑郁症患者Fp1,Fp2,F3,F4,P3,P4位点的脑电信号小波包分解后S32节点功率谱熵值和健康人存在显著差异,抑郁症患者明显大于健康人。对这一结果进行抽象分析,抑郁症病人β2节律的功率分布存在弥散性,说明神经递质分泌变化,或是神经信号传播的改变,脑细胞彼此沟通能力失调,引起脑神经电生理信号出现异常,安静闭目状态下抑郁症患者的β2节律脑电不如健康组规律,精神受压程度降低,从而引发抑郁症。这也符合现在普遍认同的抑郁症发病机制,证明了这种方法的准确性和可行性,能够为抑郁症疾病诊断提供有效的量化物理指标作为参考。
[1] 瞿 祥,王艺明.脑电非线性动力学分析在抑郁症中的应用及抗抑郁药的疗效观察[J].中国医药导报,2012,34(9):52-54,57.
[2] Ahmadlou M,Adeli H,Adeli A.Fractality analysis of frontal brain in major depressive disorder[J].International Journal of Psychophysiology Official Journal of the International Organization of Psychophysiology,2012,85(2):206-211.
[3] 王春方,张力新,张 希,等.抑郁症自发脑电信号特异性研究进展[J].中国生物医学工程学报,2014(1):86-92.
[4] Behshad H,Mohammad Hassan M,Reza R.Classifying depression patients and normal subjects using machine learning techniques and nonlinear features from EEG signal[J].Computer Methods & Programs in Biomedicine,2013,109(3):339-345.
[5] Papadimitriou S,Gatzounas D,Papadopoulos V,et al.Denoising of the fetal heart rate signal with non-linear filtering of the wavelet transform maxima[J].International Journal of Medical Informa-tics,1997,44(3):177-192.
[6] 薛缠明,李丽宏.小波分析在激光测距传感器中的应用[J].传感器与微系统,2015,34(6):151-152,160.
[7] Mendelson G.Diagnostic and statistical manual of mental disorder-s[J].Australian & New Zealand Journal of Psychiatry,2009,29(3):529-35.
[8] Jasper H H.The ten twenty electrode system of the international federation[J].Electroencephalography & Clinical Neurophysiology,1958,10:371-375.
[9] Hu A,Yan X,Xiang L.A new wind turbine fault diagnosis method based on ensemble intrinsic time-scale decomposition and WPT-fractal dimension[J].Renewable Energy,2015,83:767-768.
Feature analysis of EEG of depression based on wavelet packet node power spectral entropy*
GAI Shu-ping1,2, LIU Xin-yang1,2, LIU Jun-tao1, KONG Zhuang1,2, XU Sheng-wei1,2, CAI Xin-xia1,2
(1.State Key Laboratory of Transducer Technology,Institute of Electronics,Chinese Academy of Sciences,Beijing 100190,China; 2.University of Chinese Academy of Sciences,Beijing 10090,China)
Scalp electroencephalography(EEG)signals reflects the spontaneous rhythmic electrical physiological activities of cerebral cortex neurons,which are rich in physiological and pathological information,and important for clinical neurological and mental disease diagnosis.Aiming at condition that the depression study and diagnosis are lack of deffective quantitative parameters and quantitative indicators,present a new EEG signal analysis method based on wavelet packet decomposition,power spectrum entropy,calculate the power spectral entropy value,Wvalue of node reconstruction signal power spectrum.Apply this method to calculate and analyze the resting EEG signals.The results show that theWvalue of S32 wavelet packet node with frequency range of 24~32 Hz with depression patients are significantly larger than normal healthy people in some brain areas.It indicates that the distribution of fast EEG rhythm wave energy is more complicated and dispersive in depression patients,confirming to the pathogenesis about weak self-regulated behavior about depression patients.T-test statistical analysis is performed to prove the feasibility and accuracy of this method,provide an objective and effective quantitative physical feature indicator for depression disease diagnosis.
electroencephalography(EEG); wavelet packet transform(WPT); power spectral entropy; depression; T-test
10.13873/J.1000—9787(2017)03—0006—04
2016—04—06
国家重点基础研究发展计划资助项目 (2014CB744600);国家自然科学基金资助项目(61527815,31500800,61501426,61471342);北京市科技计划资助项目(Z141100003414015,Z141100000214002);中科院重点部署项目(KJZD—EW—L11—2)
TP 212.3; TH 703.1
A
1000—9787(2017)03—0006—04
盖淑萍(1987-),女,博士研究生,主要研究方向为多通路人体电生理信号检测系统研制和生物信息检测仪器。
蔡新霞(1966-),通讯作者,研究员,主要从事生物传感器及检测微系统的应用基础研究工作,E-mail:xxcai@mail.ie.ac.cn。

