小波变换的无缝钢轨垂向应变信号分离*

李 亮， 刘 冲， 韦佳宏， 张志新

(1.大连理工大学 辽宁省微纳米技术及系统重点实验室，辽宁 大连 116024；2.大连理工大学 机械工程学院，辽宁 大连 116024；3.大连大学 机械工程学院，辽宁 大连 116622)

小波变换的无缝钢轨垂向应变信号分离*

李 亮1， 刘 冲2， 韦佳宏1， 张志新3

(1.大连理工大学 辽宁省微纳米技术及系统重点实验室，辽宁 大连 116024；2.大连理工大学 机械工程学院，辽宁 大连 116024；3.大连大学 机械工程学院，辽宁 大连 116622)

分析钢轨垂向应变信号基线漂移产生的原因，并采用小波变换对垂向应变信号进行分解与重构，分离信号中由温度引起的应变与轮轨力产生的应变。在Matlab环境下对分布式钢轨应力检测技术与无线传感网系统数据库中垂向应变信号进行处理，结果表明，该方法可以有效地分离信号中的不同成分。

无缝钢轨； 应力监测； 小波变换； 信号分离

0 引 言

我国高速铁路速度和里程的快速增长，对列车运行的安全性检测提出了更高的要求。传统铁路检修需要大量人力物力，而且必须在停止通车后才能进行，不能对钢轨的状态实时监测。钢轨应力能够在很大程度上反映钢轨的健康状态，其中钢轨纵向应力是解算钢轨实际锁定轨温的一个重要参数，同时根据钢轨的受力状态能够计算出轮轨之间的作用力，进而计算列车安全运行的一个重要监测指标,即脱轨系数。基于钢轨应变的纵向应力与轮轨力监测的传统思路是在无缝钢轨上安装传感器，通过应变仪与数据采集卡获得钢轨应变数据，但是该方法需要试验人员现场安装与测试，因此一直作为一种钢轨应力检测的实验方案。

本文基于无线传感器网构建一套钢轨应力监测系统，并在京津线上安装运行。经过长时间对钢轨垂向应变监测，发现垂向应变信号的基线总是在一定范围内变动，很大程度上影响系统对轮轨垂向力的计算及应变极值点位置的判断。因此需要一种方法去除信号的基线漂移，同时保持垂向应变数据的特征。小波分析在信号去噪、信号分离以及图像压缩等方面有着广泛的应用[1,2]，李战明、杨守祥[3]采用了小波变换对心电信号进行分解与重构，消除心电信号基线漂移；同济大学郑玄东等人[4]运用小波分析对地铁振动信号进行降噪处理，通过分析地铁振动信号的频率分布，寻找减小地铁噪声的方法。本文采用小波变换分解垂向应变信号，提取不同分解层数下信号的特征，并通过信号中不同成分的频带差异将两者分离。

1 基线漂移原因分析

本文采取轨腰压缩量法[5]这种易于实现、工作稳定且便于防护的测试方法测量垂向轮轨力，并以此方法对运营线上的钢轨应力进行长时间监测。通过在轨腰处垂直方向粘贴应变片并组成测量电桥，测量过车过程中轮轨作用力在轨腰产生的垂向应变，经过实验标定确定垂向应变值与垂向轮轨力的关系，达到间接测量轮轨力的目的。

为了减小应变片阻值随温度变化对测量数据的影响，选用与钢轨同样材料的补偿块，通过粘贴在钢轨轨腰和补偿块上的应变片组成测量电桥来消去温度对应变片的影响[6]。由于钢轨被固定在轨道板上，纵向几乎不能伸缩，而补偿块处于完全自由状态，当钢轨温度发生变化时，两者由温度产生的应变不能完全抵消，实际测得的钢轨垂向应变信号中混杂了部分的温度力信号。图1是本文传感节点盒子京津高速铁路无缝钢轨上的安装图，负责采集钢轨温度、纵向应力、垂向应力以及过车时的加速度信号。

图1 京津线节点安装图

钢轨在自由状态与约束状态下由温度引起的应变如图2所示，自由状态下的钢轨由温度变化引起的纵向应变为εlf，垂向应变为εvf；被约束的钢轨由温度引起的纵向应变为εlr，垂向应变为εvr。本文所采用的测量系统中，轨腰处的应变片测得是钢轨约束状态下的应变，补偿块上的应变片测得的是自由状态下的应变，两者分别组成测量电桥的两个臂，电桥实际输出为

Δεv=εvr-εvf

(1)

当传感节点采集列车经过的钢轨垂向应变时，Δεv会叠加在垂向应变信号上，由于Δεv的值随着温度变化而变化，因此在一天的数据中呈现规律性的基线漂移。

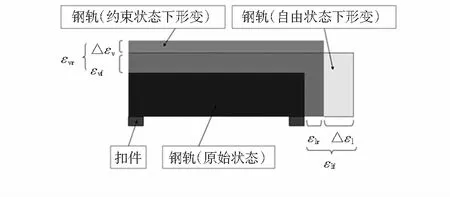
图2 钢轨随温度变化应变示意图

2 基于小波分析的信号分离方案

傅立叶变换能够将信号分解为三角波组合形式，得到信号各频率成分的幅值；但是由于其各个分量均在整个时间域内定义，只能反映信号中的频率分量，不能用于非平稳信号的分析。小波变换通过母小波函数的伸缩和平移对信号进行多尺度分析，能在高频段获得较高的时间分辨率和较低的频率分辨率，同时在低频段获得较高的频率分辨率和较低的时间分辨率[7]。

2.1 小波分析基本原理

连续小波变换[7,8]的公式为

(2)

(3)

2.2 多分辨率分析与Mallat算法

Vj=Wj-1⊕Vj-1=…=Wj-1⊕Wj-2⊕…⊕Wj-m⊕Vj-m

(4)

对于任意f(t)∈L2(R)，均能用Hilbert空间L2(R)中不同尺度下的小波空间Wj和尺度空间Vj中的基向量表示

(5)

Mallat给出了基于正交小波基的快速分解算法，即Mallat算法[8]，其算法框图如图3所示。

图3 Mallat算法框图

采样信号x通过数字滤波器g,h后，下采样得到高频系数cd1(细节)与低频(近似)系数ca1；然后对低频系数ca1进行进一步的分解，得到相对高频系数cd2和相对低频信号ca2，以此下去，信号就会被分解为一系列成分。虽然滤波器g和h不变，但由于一直在下采样，所以，其滤波带宽一直在减半。本文中待处理信号的采样频率为1 000 Hz，得到小波分解子带近似频率范围如表1所示。

3 信号分解与重构

从分布式无缝钢轨应力监测系统数据库中提取轨温数据和垂向应变数据，经过FFT处理获得其频率分布图。图4是一天的温度曲线及其频谱图，图5是过车过程中测量

表1 各尺度子带系数频率范围

点钢轨垂向应变图和频谱图，从图中可以看出垂向应变频率集中在1～200 Hz范围内，利用带通滤波器可以分离信号中的低频成分与高频成分，得到较纯净的垂向应变信号。

图4 温度信号与频谱图

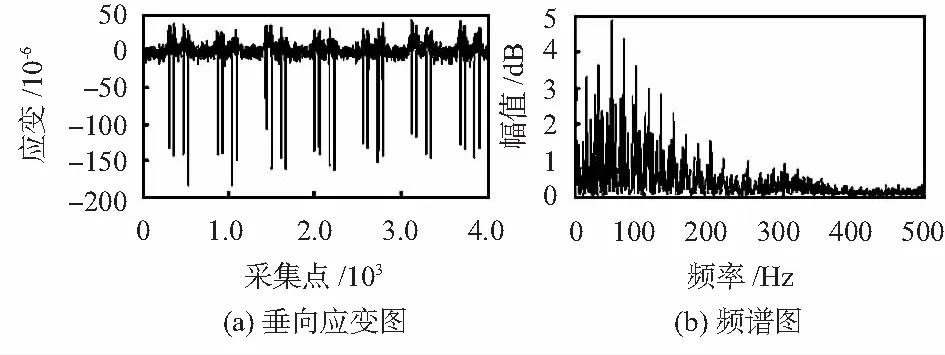
图5 垂向应变与频谱图

本文采用db4小波对分布式钢轨应力监测系统数据库中一天的垂向应变数据进行分解。信号分离步骤如下：1)读取分布式钢轨应力检测系统数据库中垂向动态应变一天的数据；2)运用db4小波对信号进行13层分解，提取各层分解的小波系数；3)对第13层分解得到的近似系数重构，得到由温度引起的应变曲线；4)将第13层近似系数进行置零处理，然后将处理后的近似系数与各个尺度的细节系数逐级重构，得到去除基线后的信号。

由图6中可以看出，随着信号的分解层数增加，其低频系数逐渐接近信号的基线，第12层分解的近似系数在几乎囊括了全部温度力产生的基线漂移信息的同时没有高频干扰以及细节丢失的情况，因此，最终选择对信号进行12层分解并重构。经过上述4个步骤之后，本文作者得到温度产生的应变以及不包含基线漂移的垂向动态应变；由此达到了分离温度力应变与垂向动态应变的目的，图7是原始信号与去除基线漂移后的信号图。

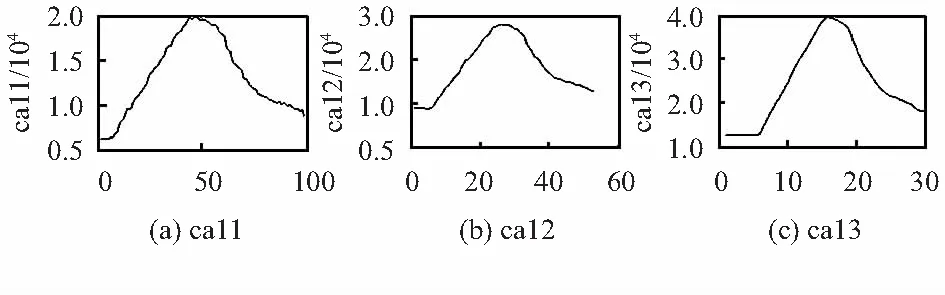
图6 不同分解层数的低频系数

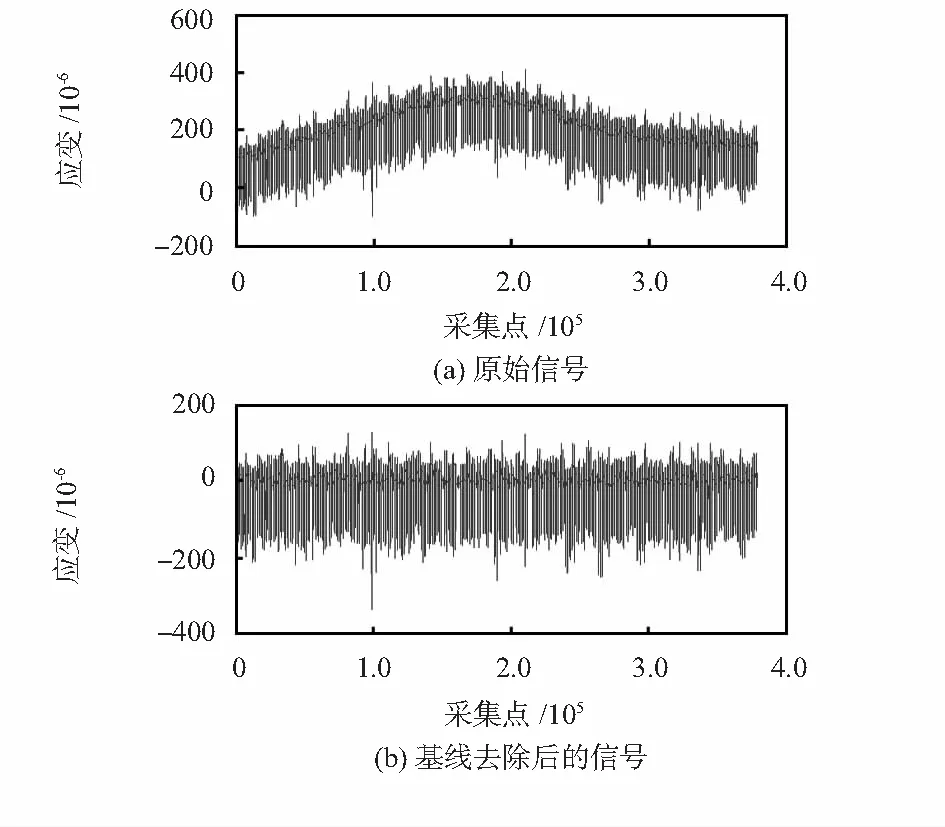
图7 原始信号与重构信号

4 信号分离效果评估

信号分离的一个基本的要求就是尽可能保留原始信号的特征，为了衡量本文小波变换方法的有效性，采取SNR评估方式对去除基线后的垂向应变进行评估。由于不包含噪声的钢轨应变信号不可能得到，因此公式(6)中的无基线漂移噪声信号也不存在；考虑到每次过车采集时间在3～4 s，忽略掉短时间内温度变化的影响，此时采集的垂向应变数据基线可以视为不变，本文中将单次过车时采集的数据为不包含基线漂移的信号y′，计算此次过车垂向应变信号的信噪比

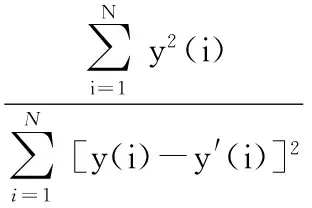
(6)

同时，提取低频重构信号，该信号完全是由温度变化导致的，将该信号与温度进行线性拟合，计算其与温度信号的线性相关系数R2，以此作为评价低频信号的分离效果。图8为db4小波经过12层分解重构后低频信号与温度线性拟合。

图8 低频分量与温度线性拟合

为了评估不同小波函数信号分离的效果，本文选取数据库中任意5天的垂向应变数据进行小波处理，得到其信噪比并取平均值。分别对不同小波函数在不同分解层数下的信号分离效果进行比较，得到信噪比与线性相关系数见表2。从表2中可以看出，采用db4小波对钢轨垂向应变信号进行12层分解重构后能达到最佳的分离效果。

5 结 论

本文阐述了轨腰压缩量法测量轮轨垂向力时基线漂移的产生原因，引用小波变换方法对垂向应变进行分解与重构，分离出高频轮轨力信号与低频温度应变信号。进一步，对比不同小波函数与不同分解层数的分离效果，得到最佳的去噪方案。最终采用db4小波对分布式钢轨应力监测系统数据库中的动态应变数据进行分解与重构，结果表明:该方法能有效地去除信号中的基线漂移，分离出温度应变，而且能够比较完整地保留垂向应变的特征。

表2 多种信号分离方案对比

[1] Zhang Zhifeng,Su Zhan,Su Yuling,et al.Denoising of sensor signals for the flange thickness measurement based on wavelet analysis[J].Optik,2011,122:681-686.

[2] Christos Yiakopoulos,Jedrzej Maczak,Konstantinos Rodopoulos,et al.Multicomponent decomposition of a time-varying acoustic Doppler signal generated by a passing railway vehicle using complex shifted Morlet wavelets[J].Transportation Research,2014,44:34-51.

[3] 李战明，杨守祥．基于提升小波的心电信号基线漂移的去除方法[J]．中国医学装备，2014,11(3):16-19.

[4] Zheng Xuandong,Geng Chuanzhi.Application of wavelet theory in subway vibration analysis[C]∥The Fourth International Conf on Transportation Engineering(ICTE),2013:1636-1642.

[5] 祖宏林，张志超，汪 伟．轮轨力测量在高速铁路轨道检测中的应用研究[J]．铁道机车车辆，2012，32 (4)：19-24．

[6] 张富生，王大志，梁军生,等．无线应变采集节点的温漂误差补偿[J]．传感器与微系统，2013,32(10):27-29．

[7] Ruch D K,Fleet P J V.Wavelet theory:An elementary approach with applications [M].New York:John Wiley & Sons,Inc.2011.

[8] 张德丰．Matlab小波分析与工程应用[M]．北京：国防工业出版社，2008．

Separation of vertical strain signal of seamless railway based on wavelet transform*

LI Liang1, LIU Chong2, WEI Jia-hong1, ZHANG Zhi-xin3

(1.Key Laboratory for Micro/Nano Technology and System of Liaoning Province,Dalian University of Technology,Dalian 116024,China; 2.School of Mechanical Engineering，Dalian University of Technology,Dalian 116024,China; 3.School of Mechanical Engineering,Dalian University,Dalian 116622,China)

Reason causes baseline drift of the vertical strain signal are analyzed,wavelet transform is used to decompose and reconstruct signal of the vertical strain,separate the strain caused by wheel-rail force and temperature.In the Matlab environment,vertical strain signal from the distributed rail stress monitoring technology and database of wireless sensor networks system are processed.The results show that the method can separate different components in signals effectively.

seamless rail; stress monitoring; wavelet transform; signal separation

10.13873/J.1000—9787(2017)03—0017—04

2016—04—14

国家“十二五”科技支撑计划项目(2011BAG05B02—03,2011BAG05B02—02)

TP 391; U 285

A

1000—9787(2017)03—0017—04

李 亮(1990-)，男，硕士,研究方向为钢轨应力监测技术与无线传感网。

刘 冲，通讯作者，E-mail：chongl@dlut.edu.cn。