基于PDR/UWB紧耦合的足绑式行人导航技术*
孙璧文, 樊启高, 武亚恒, 孙 艳
(江南大学 物联网工程学院,江苏 无锡 214122)
基于PDR/UWB紧耦合的足绑式行人导航技术*
孙璧文, 樊启高, 武亚恒, 孙 艳
(江南大学 物联网工程学院,江苏 无锡 214122)
为了解决低成本微机电惯性导航系统存在的累积误差问题,提出一种基于融合行人航迹推算(PDR)和超宽带(UWB)无线定位的实时室内行人导航系统。利用加速度计和磁强计进行初始姿态对准;考虑滤波误差估计,推导了惯性导航算法;依靠加速度计和陀螺仪的“与”逻辑进行行人步态检测;实施零速更新(ZUPT)提供速度误差观测量,利用UWB系统提供位置误差观测量;设计具有野值辨识机制的扩展卡尔曼滤波器进行数据融合。对提出的行人导航算法进行实验验证,结果表明该行人导航算法与传统定位方法相比能够有效提高行人定位精度。实验中,该行人导航算法能够获取低于0.2 m的定位误差,且稳定、不发散。
室内定位; 行人航迹推算; 超宽带; 扩展卡尔曼滤波
0 引 言
行人导航系统已经被用于定位服务、营救、运动以及军事应用等方面[1]。在室外,全球定位系统(GPS)得到广泛应用。但由于建筑物的阻挡和卫星信号衰减,GPS无法在室内进行有效定位。现有的室内定位技术可以分为两大类:无线定位系统和传感器定位系统。无线定位系统(wireless location system,WLS)通过测量距离或者角度的三角测量法来估算物体坐标。常见的无线定位系统[2]如蓝牙、WiFi、RFID,Zig Bee等,它们的定位精度易受外部环境影响,如非视距因素和多径因素。
与无线定位方式不同,传感器定位系统并不需要依附于安装好的外界设备。在导航应用方面,惯性导航系统(inertial navigation system,INS)是最常见的传感器定位系统。在过去的几年,常使用行人航迹推算(pedestrian dead reckoning,PDR)法[3]进行行人定位,需要将惯性传感器安装在身体的某个部位,通过加速度计数据与陀螺仪数据计算步长、步态以及航向等信息,来估算行人最终位置。最近微机电系统(micro-electro-mechanical system,MEMS)技术发展使得惯性测量元件更加适用于PDR方法。但是MEMS惯性传感器存在随机漂移误差以及噪声误差,长时间定位会产生很大累积误差。为了减小累积误差,部分学者提出各自的步态检测算法、步长与航向估计算法等[4~6]。这些研究都集中利用运动学规律,设计精妙算法抑制(INS)的误差,但是依旧无法避免误差累积问题。
为了彻底消除累积误差,一些学者使用INS与WiFi、RFID等[7,8]无线定位系统进行融合。这种INS+WLS的融合概念已经应用于室外GPS与INS定位,并能够提供无漂移的定位结果。在无线定位领域,超宽带(ultra wideband,UWB)系统拥有独特的定位优势,具有时间分辨率高、穿透能力强、发射功率低和数据传输速率高等特点[9]。因此,可以使用UWB无线技术来消除INS的累积误差。一些学者试图将UWB与INS技术进行融合[10],但他们研究方面只适用于车辆定位,而且INS的定位优势无法最大化利用。
本文提出一种基于足绑式惯性测量单元(inertial mea-surement unit,IMU)与UWB室内行人组合定位系统,该系统包括初始静态对准算法、IMU导航算法、行人步态检测算法、系统滤波方程以及野值辨识算法。在封闭环境下进行多种步态实验,结果表明提出的紧耦合模型算法能够获取低于0.2 m的定位精度。
1 基于IPZE/UWB算法的定位模型
利用加速度计和磁强计进行初始姿态对准;考虑滤波误差估计,推导了惯性导航算法;依靠加速度计和陀螺仪的“与”逻辑进行行人步态检测;在站立相时刻实施零速更新(zero velocity update,ZUPT)提供速度误差观测量,利用UWB系统提供位置误差观测量;设计具有野值辨识机制的扩展卡尔曼滤波器(extended Kalman filter,EKF),对位置、速度、姿态、加速度以及角速度进行最优估计,形成IPZE(INS-PDR-ZUPT-EKF)定位与UWB定位的紧耦合算法。如图1为提出的IPZE/UWB紧耦合模型。

图1 IPZE/UWB 紧耦合模型
1.1 静态初始对准
在不考虑惯性传感器误差的情况下,加速度计的输出为
(1)

(2)
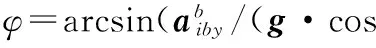
(3)
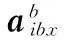
Mx=Mbxcosθ+Mbysinφ+Mbzcosφ
(4)
My=Mbycosφ-Mbz
(5)
式中Mbx,Mby和Mbz分别为磁强计的三轴输出值。Mx和My分别为磁场在n系的x轴和y轴分量。所以,航向角的计算公式
ψ=tan-1(My/Mx)-Md
(6)
式中Md为IMU所在地点的地球磁偏角。
1.2 惯性导航解算

(7)
(8)
2)姿态更新:基于k时刻的角速度和k-1时刻的姿态预测k时刻的姿态,用方向余弦矩阵表示
(9)
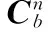
(10)
3)重力补偿:消除补偿加速度中重力的影响
(11)
4)位姿计算:位置、速度和姿态的估计。k时刻速度和位置的预测
(12)
r(k,k-1)=r(k-1,k-1)+v(k,k-1)·Δt
(13)
式中 v(k-1, k-1)和r(k-1,k-1)分别为k-1时刻的速度和位置估计。k时刻位置、速度和姿态的估计分别是
r(k,k)=r(k,k-1)-δrk
(14)
v(k,k)=v(k,k-1)-δvk
(15)
(16)
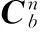
(17)
1.3 步态检测算法
当行人足部被检测到在地面静止时(站立相),EKF算法会获取到误差观测量。大部分步态检测算法仅仅依靠对加速度或者角速度设定阈值来进行站立相检测,但是在慢走或者随意行走时,这些方法会存在一些误差。本文基于多条件判别算法进行站立相判定,以提高步态检测的鲁棒性。具体判定如下:
1)加速度阈值判定条件
(18)
式中 |ak|表示k时刻加速度幅值,|ak| =[ak(1)2+ak(2)2+ak(3)2]0.5。min(Ta)和max(Ta)为设定的最小和最大加速度阈值,即|ak|在阈值范围之内,则表示C1为真。
2)角速度阈值判定条件
(19)
式中 |ωk|为k时刻角速度幅值,|ωk| =[ωk(1)2+ωk(2)2+ωk(3)2]0.5。Tω为设定的最大角速度阈值,即|ωk|小于Tω,则表示C2为真。
3)局部加速度方差判定条件
(20)
式中 σa为局部加速度方差,其具体计算方法如式(21)所示。Tσ为设定的最大阈值,即当σa小于Tσ时,表示C3为真。式(21)中,s为定义的移动窗口
(21)
(22)
只有当C1,C2和C3均为真时,则判定此时为站立相。具体的阈值设定与步态检测结果如实验部分所示。
1.4 滤波方程
由于系统状态转移模型为非线性状态函数,常规卡尔曼滤波无法处理非线性问题,因此本文使用EKF算法进行数据处理,设计一个包含15个状态量的扩展卡尔曼滤波器,其中位置误差δP、速度误差δV、姿态角(翻滚角、俯仰角以及航向角)误差δΦ、加速度误差δa以及角速度误差δω。滤波方程包括状态方程和观测方程。
1)状态方程
令状态量:X= [δP,δV,δΦ,δa,δω],系统状态方程为
δXk/k-1=FkδXk-1/k-1+Wk-1
(23)
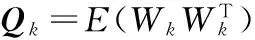
(24)
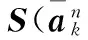
(25)
(26)
2)观测方程
观测方程模型为
Zk=HδXk/k+Vk
(27)
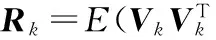
δXk/k=δXk/k-1+Kk·[Zk-HδXk/k-1]
(28)
式中Kk为卡尔曼增益,δXk/k-1是预测状态量。在本文中,系统观测量选用线速度误差Δvk以及位置误差ΔLi。
在速度误差补偿方面,当系统检测到站立相时,认定此时脚的真实速度为0 m/s。将惯性导航测量的实际速度与真实速度之差Δvk作为此时速度的观测量,其相应的观测矩阵如下
H1=[03×3I3×303×303×303×3]
(29)
在位置误差补偿方面,使用UWB定位系统对位置进行修正,因此需建立相应的位置观测方程。设置UWB锚节点的矢量坐标为pi=[xi,yi]T,i=1,2,…,N,其中N是定位基站总数。在k时刻,盲节点的矢量坐标是puwb=[xuwb,yuwb]T,惯性导航测量出行人的位置是pins=[xins,yins]T。由于盲节点安装在行人身上,因此,盲节点到第i个锚节点间的距离为
duwb,i=‖puwb-pi‖
(30)
dins,i=‖pins-pi‖
(31)
由式(30)和式(31)可得
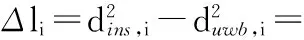
(32)
将第2~N个等式依次减去第1个等式,得到UWB定位误差观测量
ΔLi=Δli-Δl1=-2(p1pins-p1pins-pipuwb+p1puwb)=
-2(pi-p1)×Δp
(33)
式中Δp=pins-puwb,i=2…N。结合式(29)和式(33)可得系统观测量和观测矩阵
Zk=[Δvk,ΔL2,…,ΔLN]T
(34)
(35)
(36)
本系统只考虑二维平面坐标定位,因此Z轴方向上的观测量设为0。
1.5 野值辨识机制
在实际运动过程中,UWB系统实时测量当前行人位置。而UWB测量值很容易受到环境干扰,产生野值。所以需要对野值进行辨识并修正,这样才能使得EKF滤波器稳定与收敛。因此基于新息正交性理论,有如下等式
(37)
记
(38)
根据式(38)两边矩阵的对角线元素,对量测量Zk的位置误差分量Zi,k是否为野值进行假设判断,判别如下
Bi,k∈[Mi,k-εi,Mi,k+εi]
(39)
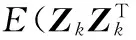
(40)
在每个滤波周期内,对量测量Zk中各个分量分别进行野值辨识。当Zk不是野值时,权重因子为单位值,不改变新息序列;而当Zk为野值时,则使用小于1的活化函数进行加权限制,保持新息的正交性。使用具有抗野值机制的EKF算法对PDR/UWB组合系统进行融合滤波,提高整个系统的容错能力以及定位精度。
2 实 验
2.1 实验设置
为了评估提出的紧耦合模型的定位效果,需要对实验环境进行相关配置。本文使用Xsens公司的MTi微惯性航姿模块以及一套UBW无线定位系统作为实验装置。其中,微惯性航姿模块包含三轴加速度计、三轴陀螺仪以及三轴磁强计等传感器,输出速率为100 Hz/s,通过USB数据线与电脑通信;UBW无线系统的输出速率为10 Hz/s,通过无线装置与电脑进行通信,并使用电脑对数据进行分析;EKF的更新频率为100 Hz。将IMU模块固定在脚上,接收惯性数据;将超宽带定位标签固定在肩膀上。实验装置如图2所示。
分别进行三种不同实验来证明算法的有效性。第一种是普通行走实验,包括直线行走、拐弯等步态;第二种是快速跑步实验,轨迹为一个矩形;而第三种是按照圆形轨迹行走。设定实验环境:实验是在8 m×5 m的室内进行。步行实验是从(1,1)点开始行走,经过(3,1),(5,4),(7,4),(7,1),(5,1),(3,1),(1,3),最终回到(1,1)点;跑步实验是从(1,1)点开始走,经过(7,1),(7,4),(1,4)点,最后回到(1,1)点;最后的圆形轨迹行走实验是以(3,2.5)为圆心,以1 m为半径进行的。为了使得位置误差累积效果明显,进行多次重复行走。本文中步行实验重复了4圈相同轨迹,跑步实验重复了5圈相同轨迹,圆形行走实验重复了10圈相同轨迹。

图2 实验设备图
为了检测站立相,设定阈值max(Ta)=11m/s2,min(Ta)=9m/s2,Tσ=2m/s2,Tω=50°/s,S=17。站立相检测过程如图3所示。只有当C1,C2和C3全部为真时,才属于站立相时刻。从图中可以观察出单独的线加速度或者角速度无法准确捕捉到站立相,因此,这种“和”逻辑的方式能够提高系统的鲁棒性。
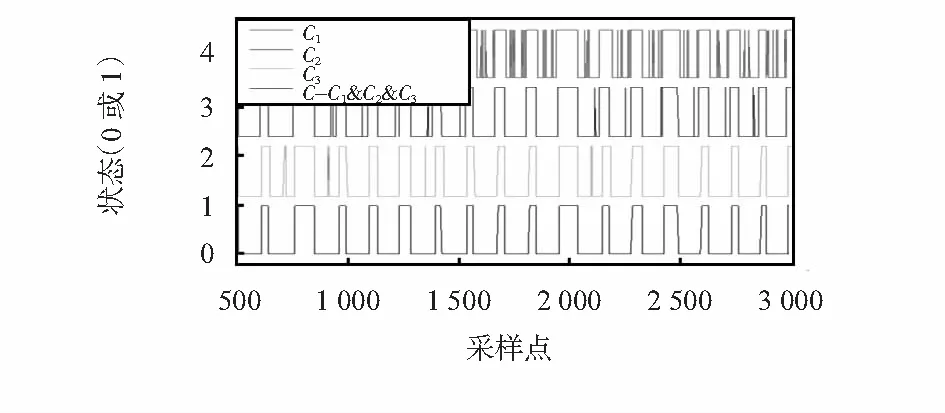
图3 步态检测图
2.2 测试与分析
普通行走、快速跑步以及圆形轨迹行走三种步态实验轨迹如图4。可以观察出:MEMS惯性导航单独定位效果最差,定位轨迹与实际最不相符合;IPZE算法解算偏差随行走的圈数增多而不断变大;UWB定位效果整体上误差很小,但存在个别位置误差较大的野值;而本文提出的IPZE/UWB算法定位效果明显优于前面提到的定位方法,且能够应对各种环境的影响。接下来会利用数据进行更进一步验证。
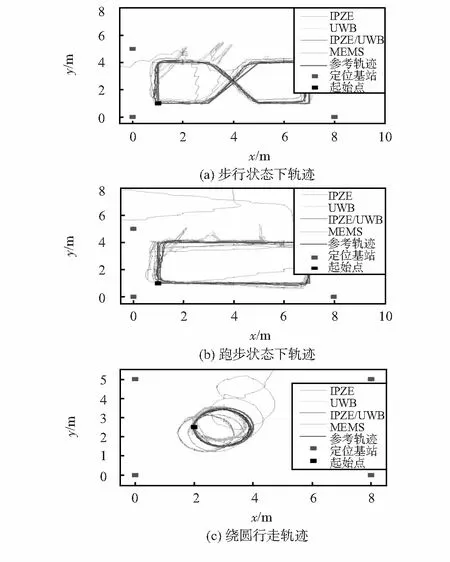
图4 不同步态下轨迹
在实验中,进行了直线行走、拐弯、跑步、圆形行走等多种步态测试,均为封闭轨迹。实验误差曲线如图5所示。由于MEMS单独定位误差太大,故在此不对其进行误差分析。图6为不同步态、不同定位策略下的平均误差图。
由图可知,步行状态下,IPZE算法的误差范围为-0.293 3~1.886 7m,平均误差为0.196 5m,平均残差率为8.21 %,置信度为91.79 %;UWB定位的误差范围为-0.316 5~0.298 2m,平均误差为0.142 3m,平均残差率为7.09 %,置信度为92.91 %;而提出的IPZE/UWB方法的误差范围为-0.516 5~0.108 2m,平均误差为0.100 1m,平均残差率为4.06 %,置信度为95.94 %。IPZE/UWB算法的定位精度比IPZE算法提高了49.06 %,比UWB定位提高了29.65 %。

图5 不同状态下位置误差
跑步状态下,IPZE算法的误差范围为-0.756 6~0.252 2m,平均误差为0.166 8m,平均残差率为9.32 %,置信度为90.68 %;UWB定位的误差范围为-0.400 0~1.140 0m,平均误差为0.133 1m,平均残差率为7.39 %,置信度为92.61 %;而提出的IPZE/UWB算法的误差范围为-0.355 6~0.313 0m,平均误差为0.070 2m,平均残差率为4.42 %,置信度为95.58 %。IPZE/UWB算法的定位精度比IPZE算法提高了57.91 %,比UWB定位提高了47.26 %。
绕圆运动时,IPZE算法的误差范围为-0.198 6~1.158 1m,平均误差为0.360 9m,平均残差率为9.44 %,置信度为90.56%;UWB定位的误差范围为-0.196 5~0.610 2m,平均误差为0.127 9m,平均残差率为4.47 %,置信度为95.53 %;而提出的IPZE/UWB算法的误差范围为-0.196 9~0.519 9m,平均误差为0.110 0m,平均残差率为4.00 %,置信度为96.00 %。IPZE/UWB算法的定位精度比IPZE算法提高了69.52 %,比UWB定位提高了13.99 %。
图6 不同步态下平均误差图
2.3 讨 论
一方面,对于不同的步态来说,判断站立相的理论条件上应当是相同的,但是由于运动的剧烈性和方向性不同,判断站立相的依据也应该有所改变,以适应步态的变化;另一方面,UWB定位结果易受多径因素和非视距因素影响,且成本较大,定位范围较小,运动空间受局限,所以,应该尽量提高纯惯性导航定位精度或可以在必要的通道或者节点处安放无线定位装置进行校正,提高此方法的实用性。
3 结 论
实验结果表明提出的紧耦合算法定位效果稳定且不发散,能够获取到低于0.2 m的定位误差。对于进行研究惯性定位技术以及其组合定位技术具有很好的参考和应用价值。
[1] Foxlin E.Pedestrian tracking with shoe-mounted inertial sensor-s[J].IEEE Computer Graphics and Applications,2005,25(6):38-46.
[2] Liu H,Darabi H,Banerjee P,et al.Survey of wireless indoor positioning techniques and systems[J].IEEE Transactions on Systems Man and Cybernetics:Part C—Applications and Reviews,2007,37(6):1067-1080.
[3] 李金凤,王庆辉,刘晓梅,等.基于MEMS惯性传感器的行人航位推算系统[J].传感器与微系统,2014,33(12):85-87.
[4] Zhang Z Q,Meng X L.Use of an inertial/magnetic sensor module for pedestrian tracking during normal walking[J].IEEE Transactions on Instrumentation and Measurement,2015,64(3):766-783.
[5] Fourati H.Heterogeneous data fusion algorithm for pedestrian navigation via foot-mounted inertial measurement unit and complementary filter[J].IEEE Transactions on Instrumentation and Measurement,2015,64(1):221-229.
[6] Diaz E M.Inertial pocket navigation system:Unaided 3D positioning[J].Sensors,2015,15(4):9156-9178.
[7] Zhuang Y,Lan H,Li Y,et al.PDR/INS/WiFi integration based on handheld devices for indoor pedestrian navigation[J].Micromachines,2015,6(6):793-812.
[8] Jimenez Ruiz A R,Seco Granja F,Prieto Honorato J C,et al.Accurate pedestrian indoor navigation by tightly coupling foot-mounted IMU and RFID measurements[J].IEEE Transactions on Instrumentation and Measurement,2012,61(1):178-189.
[9] 邬春明,耿 强,刘 杰,等.DGPS与UWB混合精确无缝定位技术研究[J].传感器与微系统,2012,31(3):74-77.
[10] Angelis A de,Nilsson J O,Skog I,et al.Indoor positioning by ultrawide band radio aided inertial navigation[J].Metrology and Measurement Systems,2010,17(3):447-460.
Foot-mounted pedestrian navigation technology based on tightly coupled PDR/UWB*
SUN Bi-wen, FAN Qi-gao, WU Ya-heng, SUN Yan
(School of IoT Engineering,Jiangnan University,Wuxi 214122,China)
In order to solve accumulated error problem of low cost micro-electro-mechanical inertial navigation system,a new real-time indoor pedestrian navigation system based on fusion of pedestrian dead reckoning (PDR)and ultra wideband(UWB)wireless positioning is proposed.The accelerometer and magnetometer are used to calculate the initial attitude;inertial navigation algorithm is deduced by considering the filtering error estimation;the“and”logic is used in step detection algorithm by relying on the accelerometer and gyroscope;zero velocity update(ZUPT)is carried out to provide velocity error measurements and UWB system is used to provide position error measurements for the filter;an extended Kalman filter with the outliers identification mechanism is designed for data fusion.The proposed pedestrian navigation algorithm is verified,and the proposed algorithm can effectively improve the positioning position of pedestrian compared with the traditional method.In the experiment,the pedestrian navigation algorithm can obtain the positioning error which is less than 0.2 m.The proposed navigation system is stable and divergence problem does not exist.
indoor positioning; pedestrian dead reckoning(PDR); ultra wideband(UWB); extended Kalman filtering(EKF)
10.13873/J.1000—9787(2017)03—0043—05
2016—03—29
国家自然科学基金资助项目(51405198);中央高校专项自主科研项目(JUSRP11464);江苏省2015年度普通高校研究生实践创新计划项目(SJLX15_0567)
TP 212
A
1000—9787(2017)03—0043—05
孙璧文(1991-),男,硕士研究生,研究方向为封闭环境下导航定位。
樊启高(1986-),男,通讯作者,博士,讲师,从事智能传感与测量系统研究工作,E-mail:qgfan@jiangnan.edu.cn。

