三平移混联机构型综合

葛姝翌 曹 毅 周 睿 朱景原 丁泽华

1.江南大学机械工程学院,无锡,2141222.上海交通大学系统控制与信息处理教育部重点实验室,上海,2002403.上海交通大学机械系统与振动国家重点实验室,上海,2002404.江苏省食品先进制造装备技术重点实验室,无锡,214122

三平移混联机构型综合

葛姝翌1,4曹 毅1,2,3,4周 睿1,4朱景原1,4丁泽华1,4

1.江南大学机械工程学院,无锡,2141222.上海交通大学系统控制与信息处理教育部重点实验室,上海,2002403.上海交通大学机械系统与振动国家重点实验室,上海,2002404.江苏省食品先进制造装备技术重点实验室,无锡,214122

针对三平移三自由度混联机构，基于分形理论和机构拓扑图，提出了一种有效的型综合与分析方法。首先，介绍了机构拓扑图和分形理论的概念及联系；其次，叙述了机构的运动特征和运算法则；再次，建立了混联机构与分形的关系模型，从而归纳出混联机构构型综合的具体步骤，并综合出具有三平移运动特征的混联机构；最后，提出了混联机构运动特征的分析方法，并按该方法分析了所综合出的三平移混联机构的末端运动特征，从而验证了该构型的正确性，证实了所提出方法的可行性。

混联机构；构型综合；分形理论；三平移

0 引言

串联机构具有控制灵活、工作空间较大的优点，并联机构具有高刚度、高速度、高精度的优点。但是，随着机构学研究的不断延伸，人们对于机构的输出提出了更高的要求。近年来，一些学者将研究视角对准了混联机构，混联机构兼具串联机构和并联机构的优势，同时又能避免单纯串联或并联机器人所带来的问题，在现代制造业中更具有实用性，是今后机构学研究的一个重要发展方向。国内外制造业中，混联机构已被设计并成功应用于多种混联机器人，如瑞典NeosRobotic公司生产的Tricept系列机器人、德国DS-Technology公司生产的Exechon机器人、AdeptTechnology公司生产的AdeptQuattro机器人[1-4]、吴孟丽等[5]发明的TriVariant系列机器。

目前，国内外对于混联机器人构型综合的设计理论与方法已有一些成果：国内，李秦川等[6]根据约束螺旋特性和几何条件,建立了少自由度并联机器人机构型综合理论；郭盛等[7]结合运动子群和螺旋理论的概念，提出了非过约束对称四自由度并联机构的设计和综合方法；杨廷力等[8-9]提出了以单开链支路为单元的三平移并联机器人机构型综合方法；沈惠平等[10-11]提出了基于方位特征集和自由度分配的混联机构设计方法；刘海涛等[12]基于单调性分析实现了对少自由度机器人的尺寸综合；GAO等[13-14]基于单开链和复合运动副综合出少自由度机器人机构。国外，文献[15-18]基于螺旋理论并依据几何描述法综合2-4自由度并联机构构型；HERVÉ[19]在李群及其子群数学方法的基础上形成了全新的构型综合理论；GOGU[20]针对各向同性的特征对并联机器人进行综合；相关的混联机构综合方法还包括其他不同的混联综合方法[21-22]。

综上所述，不难发现上述混联机器人机构可划分为以下三种形式：①并联机构通过其他机构串联而成；②并联机构直接串联在一起；③在并联机构的支链中采用不同的结构。混联机器人机构的型综合主要关注支链的设计方法，其支链的布局较为单一。因此，以上理论不适用于具有多路径横向非典型性的混联机构的构型设计。

基于分形理论和机构拓扑图，本文提出了一种简单有效的混联机器人构型综合理论和设计方法，通过建立混联机构与分形的关系模型和归纳出混联机构构型综合的具体步骤，综合出具有三移动(3T)运动特征的混联机构，最后通过实例验证其可行性。

1 分形理论和机构拓扑图

1.1 分形理论的基本概念

数学家MANDELBROT首次提出了分形几何理论的概念[23]。其中，分形的两个定义如下[24]：①如果一个集合在欧氏空间中的豪斯多夫维数D严格大于其拓扑维数DT，则该集合为分形集，简称为分形；②组成部分以某种方式与整体相似的形体称为分形。

分形理论定义中的两个变量D和DT，其含义为它们都对Euclidean空间中的每一个集合R赋予一个实数，且将此实数定义为该集合的维数。其中，DT是其中较为直观的拓扑维，另一个就是由Hausdorff提出分形维数的D。两个维数无需相等，其中，DT必须是整数，它们需要满足Szpilrajn不等式：

D≥DT

(1)

1.2 机构拓扑图

静平台、动平台和支链构成了机构拓扑图。静平台为固定平台，动平台为机构末端输出，支链用于连接静平台和动平台。

机构拓扑图是混联机构的设计基础，其重要内容如下：首先将混联机构简化为连杆机构，其次确定机构构型拓扑布局，再次展开路径与支链的结构设计，最后实现混联机构的整体构型设计。将分形理论引入到机构拓扑图中，衍生出三种分形方式：链分形、平台分形、链台分形[25-27]，如图1所示。

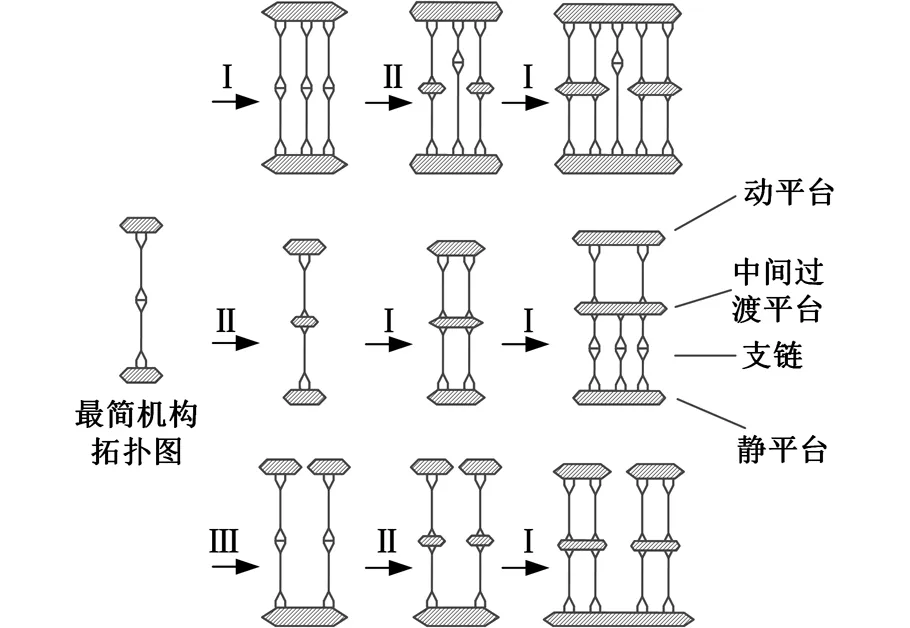
Ⅰ.链分形 Ⅱ.平台分形 Ⅲ.链台分形图1 机构拓扑图分形途径Fig.1 Fractalform of topological graph

1.3 分形方式的具体分析

1.3.1 链分形的定义

通过一个或多个运动副连接两个平台，则称该运动副的组合为支链。链分形是对支链进行的分形(图1中Ⅰ所示)，可以细分为纵向链分形和横向链分形。

1.3.2 平台分形的定义

平台分形(图1中Ⅱ所示)是指把已存在的支链打开，加入新的过渡平台，再连接新平台两端的支链。值得注意的是，拓扑机构只能在已有支链的位置进行平台分形。

1.3.3 链台分形的定义

链台分形(图1中Ⅲ所示)是指在任意平台上分形出一个支链和一个平台的分形方式，且新生成的平台为独立输出，不与机构的输出动平台有任何联动关系，即得到多输出动平台的拓扑机构。

必须指出的是，链分形和平台分形输出的拓扑结构为闭环拓扑结构，即输出平台有且仅有一个。链台分形输出的拓扑结构为开环拓扑结构，即输出动平台不止一个，适用于多点工作平台环境。由于开环结构一般较为简单，本文主要考虑闭环拓扑结构，故链台分形在本文中未予考虑。

2 机构运动特征和运算法则的描述

转变由机构拓扑图到混联机构构型，需要经历从机构拓扑图生成拓扑路径，由拓扑路径定义机构支链，再由支链适配具有给定末端输出特征的运动副，共三个阶段。

2.1 路径及路径法则

2.1.1 路径的概念

由设计的三个阶段不难发现，路径是混联机构设计的核心元素，故路径的设计及运算法则具有重要意义。

由连接末端动平台、静平台和中间过渡平台的支链按照一定方式组合而成路径，路径始于静平台，终于动平台，与过渡平台无关。其中，规定每条路径所含支链为串联关系，规定各路径之间为并联关系。根据以上规定，即可通过各支链进行交集和并集的计算结果得到动平台的输出位移子集：

(2)

其中，Bij表示第j条路径的第i个支链末端输出位移子集；Rj表示路径输出位移子集；P表示机构末端动平台输出位移子集；I表示第j条路径的支链总数；J表示路径总数。当存在横向支链时，不同路径会发生共用同一支链的现象。#代表串联运算符，&代表并联运算符。

2.1.2 路径法则

路径法则即基于机构拓扑图，对于给定的机构动平台末端输出位移子集，找出所有满足条件的路径及其支链配置。由于机构拓扑图图形复杂，将其分为以下两种情况分别进行分析：

(1)一般机构拓扑图——机构拓扑图中存在公用平台。那么路径可以由同一支链串联不同支链即同一支链重复利用而得，如图2所示。

图2 一般机构拓扑图Fig.2 A normal topological graph

通用路径数目计算公式为

(3)

式中，J为路径数量；n为公共平台数目；ai1为在第i公共平台中位于下位的支链数量；ai1为在第i公共平台中位于上位的支链数量。

(2) 存在横向支链的机构拓扑图，示例如图3所示。不难发现该机构拓扑图路径分配状况复杂，且存在共用支链的状况。

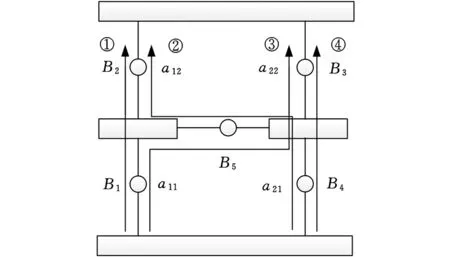
图3 存在横向支链的拓扑图Fig.3 Topological graph with horizontal branches

由图3可知，静平台和动平台之间的路径组成情况为：B1B2、B1B5B3、B3B4、B4B5B2。那么，通过支链情况计算路径的数目为

J=a11a12+a11a22+a12a21+a12a22

(4)

图3是分类(2)中最简易的机构拓扑图，只存在一个横向链分形。机构拓扑图多次横向链分形，且每两个过渡平台都通过横向支链两两连接，不仅是横向链分形最复杂的情况，而且是路径法则分析最复杂的情况。因此，通过表1分阶段对每种机构拓扑图进行分析，并从表1中归纳出路径计算公式。

(1)点到点的路径数目，是指由某一过渡平台出发，到达另一过渡平台所经过的路径的数目，由表1可以得出an：

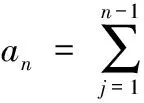
(5)

(2)累计增加路径数目，是指与去除横向支链后的机构拓扑图相比，该机构拓扑图所增加的路径数目cn：

cn=n(n+1)an

(6)

经分析可得复杂机构拓扑图的路径法则的两个重要模块：①去除横向支链剩下的一般机构拓扑图；②与一般拓扑图对比增加的路径数量。机构拓扑图的路径数量就是两者的和。

2.2 支链及串并联计算法则

2.2.1 支链与分形的关联

支链作为机构拓扑图的重要组成部分，也是分形过程中最重要的组成结构。因此，分形和支链间存在密不可分的关系，具体如图4所示。

图4 平台分形与支链的关系Fig.4 Relationship between platform fractal and branches

序号1234三维拓扑图横向支链俯视结构图路径分析an12516cn21260320

链分形可以分为横向链分形和纵向链分形，其与支链及路径的关系归纳为图5。

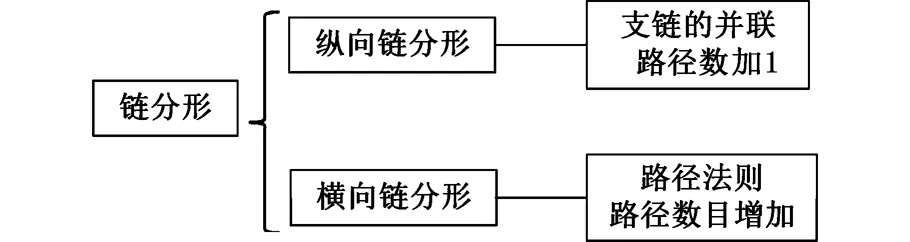
图5 链分形与支链的关系Fig.5 Relationship between branch fractal and branches

2.2.2 串并联计算法则

从构型的角度看，机构由路径并联而成，路径由支链串联而成；从数理逻辑的角度看，各路径输出位移子集求交集生成机构末端输出位移子集，各支链的输出位移子集求并集生成对应支链的输出位移子集。

由于非正则关系的原因，故在计算中不引入方位关系。串并联计算法则定义为

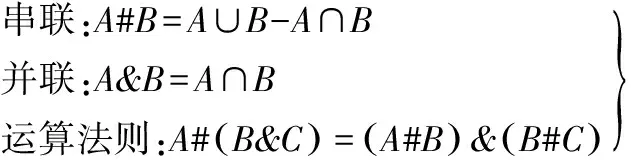
(7)

式中，A、B为输出位移子集；∪为求并运算符；∩为求交运算符。

2.3 运动副的表达

运动副是组成支链的基本元素，因此，运动副的描述对于混联机构设计具有重要意义。为使运动副的表达更加简洁明了，本文提出了8位二进制码的表达方式，其不仅能清楚地阐述运动副的种类、与基坐标轴的位置关系、相邻运动副轴线的方位关系及平台和支链间的连接关系，而且应当指出的是，二进制代码的表达方式还有利于后续的数字化设计。

2.3.1 运动副的表达形式

首先，依据运动副的类别和位置关系，单一运动副选用5位二进制码的表示方式，具体见表2。

表2 单一运动副二进制表示方法

单一运动副可细分为六种情况，如图6所示。

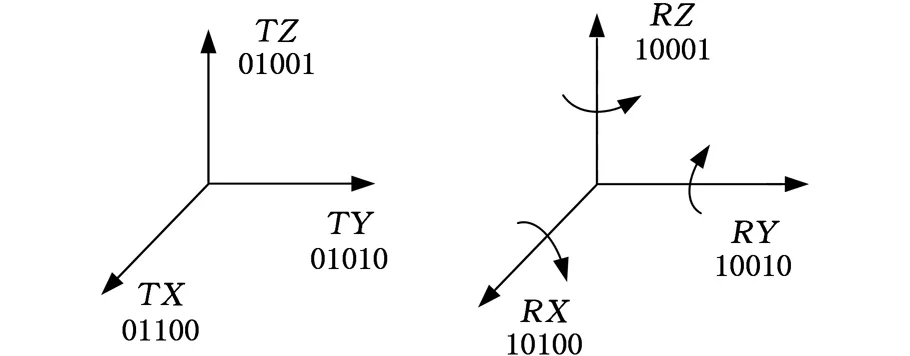
图6 运动副的描述Fig.6 Description of kinematic pair

表1可划分为前后两部分，表征不同的含义：

(1) P0.4和P0.3为运动副类别位R、T，若P0.3=1，则表示运动副为移动副；若P0.4=1，则表示运动副为转动副，且两者不能同时为1。

(2) P0.2、P0.1和P0.0为运动副轴线方向位X、Y、Z，此方向位的矢量方向与基坐标轴方向一致，若P0.0=1，则表示运动副的轴线与基坐标轴的Z轴平行；同理可得P0.1、P0.2，且方向位最多只能有一位为1。

2.3.2 相邻运动副间轴线的方位关系

由于单一运动副中的方向位只能表示相邻运动副间轴线的部分方位关系，为全面表征各运动副之间的方位关系，需使用3位二进制码进一步描述相邻运动副间的方位关系，见表3。

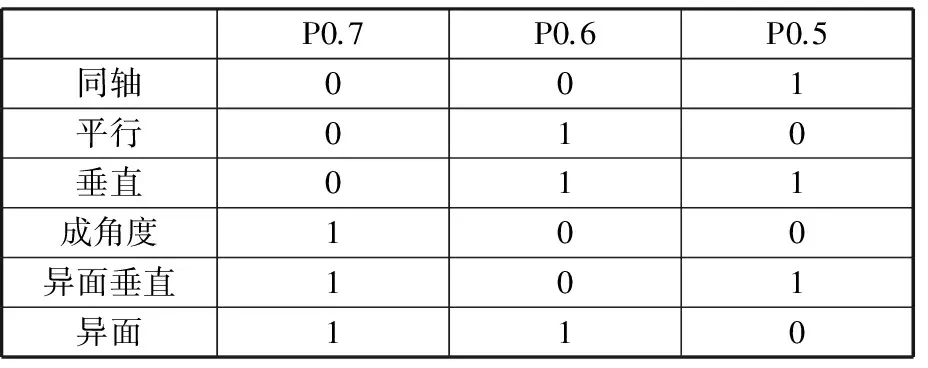
表3 运动副的方位关系的表达方法Tab.3 Expression of position relationship of adjacent kinematic pair

应当指出的是，大多数方位关系均具有传递性，例如平行、同轴等。具有传递性的方位关系为正则方位关系，其余为非正则关系[28]。

由于三维空间的一个直线矢量在三个方向需要三个以上的相对位姿关系才能完全约束其方向，单一采取一组相邻的运动副轴线的相对位置关系是不充分的，因此，在相邻运动副的基础上需要再添加一组运动副轴线的位置关系作为辅助元素，即一个运动副的轴线方向由相邻的运动副和相隔的运动副所决定。

3 3T混联机构构型综合

3.1 混联机构构型综合依据

混联机器人的构型设计是基于机构的拓扑结构适配相应的运动副，并判定适配运动副的布局是否符合设计的过程。基于分形类别，混联机器人被分成两类：第一类，具有横向支链的机构拓扑图，且可通过后续分形得到三维分形的混联机构，如图7所示；第二类，不具备横向支链的机构拓扑图，即不存在横向链分形的可能，如图8所示。

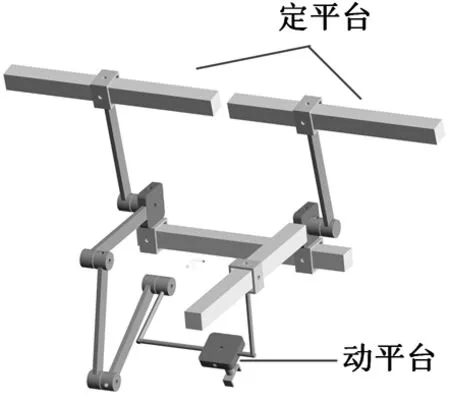
图7 第一类混联机器人Fig.7 First class of hybrid robot

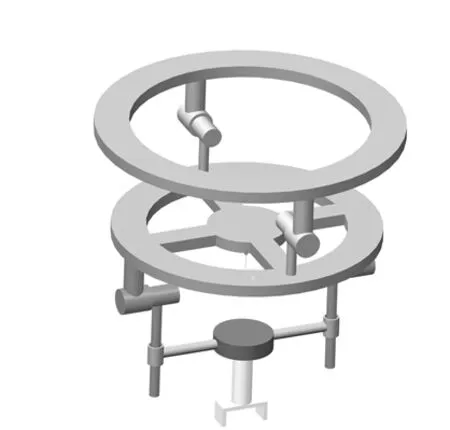
图8 第二类混联机器人Fig.8 Second class of hybrid robot

从集合的角度，路径首先按照一定的准则并联组成混联机构；然后，支链通过串联的方式组成路径；最后，运动副通过自由度分配合成支链。式(2)是其组成关系依据，式(7)是其运算法则依据。

式(2)表明，混联机构的型综合的中心内容是：在选定的拓扑机构和计算法则的基础上，第一步确定路径，第二步确定支链，最后选取运动副，并判定其正确性。

由上文可知，混联机构是以机构拓扑图为基础的，而机构拓扑图又是建立在分形的基础上的。则确定机构拓扑图之后，随之确定路径、支链，再依据机构输出位移子集对运动副的自由度进行分配。因此，有必要建立分形与混联机构的关系模型：

(8)

式中，Fdof为机构自由度数；Ri为第i个支链上的驱动运动副数(i=1,2,…,n)；N为分形次数；b为被动支链数；n为主动支链数；L为链分形次数；P为平台分形次数；Pmin为最短支链的平台分形次数。

基于分形理论的混联机器人构型的特点如下：

(1) 该构型方法的主要思想是以最短路径为中心对机构拓扑图进行扩展，其他路径是最短路径输出位移子集的父集，因此，不存在瞬时性。

(2)由于混联机构构型设计的基础为机构拓扑图，而分形理论可以实现其变化的多样性，因此，该设计方法可以实现混联机构设计的多样化。

(3)采用单元代换原理用于实现支链的替代化设计。将满足条件的机构或者运动副等代入支链中，完成该支链的期望末端运动特征。需注意的是所代入的机构所包含的支链数小于所设计的混联机构的支链数。

3.2 混联机构构型综合步骤

根据上述设计方法，得到构型综合步骤如下：

(1) 根据给定的机构末端输出位移子集，确定最简拓扑图的链分形、平台分形的次数，并绘制机构拓扑图。

(2) 运用路径法则分析该机构拓扑图的输出位移子集计算公式和路径数目，并确定最短路径所在位置。

(3) 根据步骤(2)中的计算公式，并参考各支链的串并联关系，采用MATLAB编程或者列举的方式获得满足条件的路径自由度和支链的输出位移子集，完成适配运动副的过程。

(4) 通过式(7)计算上述支链、路径的输出位移子集，并得出机构末端输出位移子集，与预计输出位移子集进行对比，若一致，则证明了该设计方法的可行性。

(5) 获得混联机构构型，绘制三维图像。

为了更加清楚表现具体设计步骤，用流程图(图9)来反映设计流程。

图9 混联机器人构型综合流程图Fig.9 A design flowchart of hybrid robot

3.3 3T类混联机构构型综合

由于分形使得机构拓扑图具有多样性，故本文所涉及的构型综合，是在已选定的拓扑机构图的基础上，对此类型的混联机构进行构型综合，如图10所示。

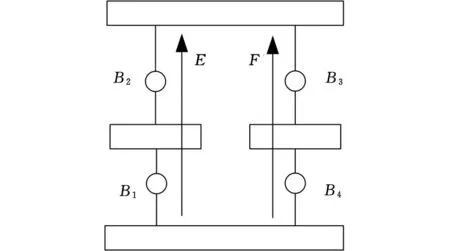
图10 选定机构拓扑图Fig.10 A selected topological graph

运用3.1节和3.2节中的综合方法和步骤对3T混联机构进行构型综合。通过路径法则(式(2))的分析可知，路径共有以下2条：

{B1B2，B3B4}

(9)

取B1B2为最短路径，其中，B1支链的输出位移子集为T(U)T(V)，B2支链的输出位移子集为T(W)。与此同时，对其他路径的自由度进行分析，前提条件是具有3T特征或者3T父集的特征集合：

{1R3T, 2R3T, 3R3T}

(10)

对式(10)进行排列组合，并挑选符合构型条件的组合，可得到除最短路径之外所有路径的组成形式。当路径B3B4的输出位移子集满足式(10)的所有解集，则可作为支链设计所选择的支链的位移子集。

一般地，选取最短路径上的支链作为安装驱动的位置，即B1B2为主动支链，剩余支链为被动支链。为简化表达，路径B1B2为E，路径B3B4为F，要求各支链满足下式：

(11)

依据式(11)求解支链B3B4的输出位移子集，并归纳出其构型类别，见表4。

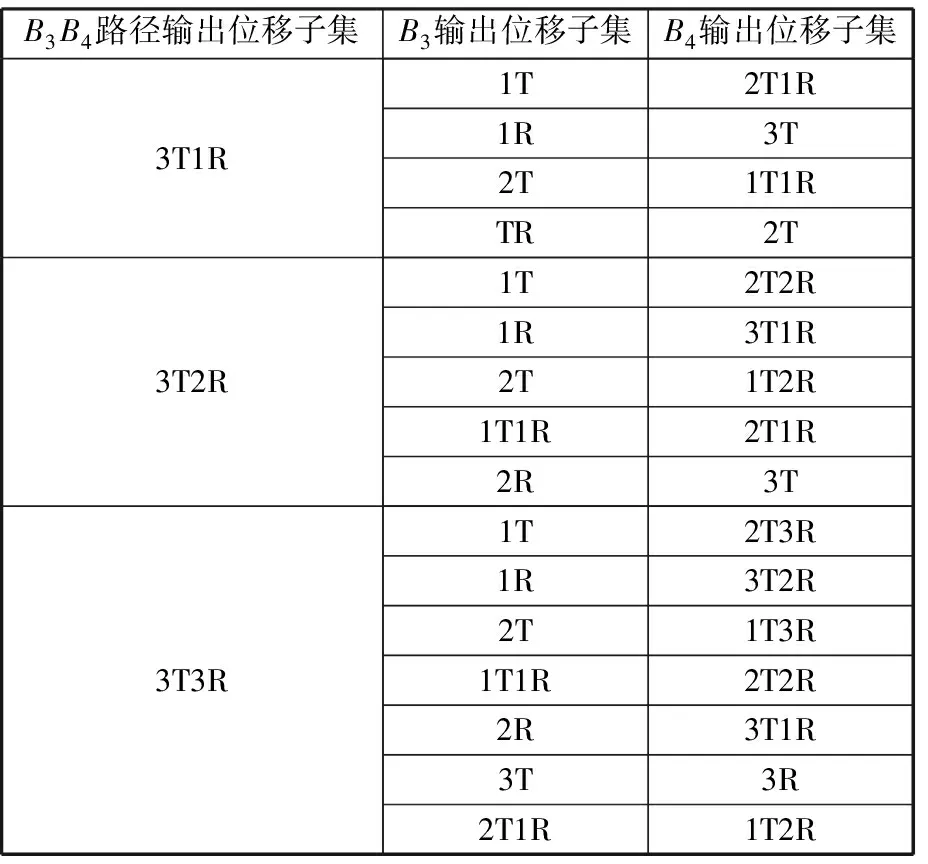
表4 混联机构B3B4输出位移子集类型Tab.4 Type of displacement set of B3B4 in the hybrid mechanism

从表4中选取一组数据作为所有支链的输出位移子集，按照图10的机构拓扑简图构造出输出为3T的混联机构构型。

4 机构构型验证及分析

4.1 混联机构末端运动特征分析

本文提出了混联机构末端运动特征分析方法，用于验证上文综合出的3T三自由度混联机构的正确性。其分析方法的基本思路如下。

(1) 对混联机构构型进行分析，将其分割为机构拓扑图和支链这两部分。

(2) 基于2.3节中的内容，将运动副转换为二进制代码的表现形式。

(3) 运用式(7)将支链中的运动副以串联运算方式推导出各支链的输出位移子集。

(4) 运用路径法则分析步骤(2)中所得的机构拓扑图得到各路径分支，在步骤(2)的基础上，通过数理逻辑关系得到各路径的输出位移子集。

(5) 通过路径的并联运算方式得到混联机构动平台的输出位移子集，即混联机构整体的末端运动特征。

4.2 机构自由度分析

以表4中选取一组数据举例说明，该混联机构各支链的输出位移子集见表5。

表5 支链适配运动副

根据选择的机构拓扑图和适配的运动副绘制混联机器人，如图11所示。

图11 输出3T的混联机构Fig.11 A 3D model of 3T hybrid mechanism

为确保所综合出的机构构型的正确性，核算各支链的输出位移子集，并求取机构末端输出位移子集与预期对比，计算过程如下：

(12)

B2=TZ(〗WTBX〗(W)=[06 09 04]TH

(13)

(14)

其中，下标H表示矩阵中的元素为十六进制数。结合式(7)和式(12)～式(14)可推导出各路径的输出位移子集：

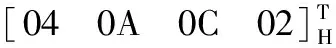
(15)

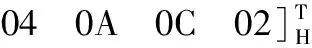
(16)

由式(15)～式(16)可得机构末端动平台的输出位移子集：

综上所述，动平台的输出位移子集与B1B2路径的输出位移子集相同，且和已知输出相同，证明结果正确，从而验证了上述混联机构型设计方法的正确性。

5 结论

(1) 本文根据分形理论建立了对拓扑结构图的有序分形，并通过对运动副的分配及输出位移子集的排列组合，实现了混联机器人机构构型的多样化。

(2) 提出的路径法则可用于求解复杂机构拓扑图的多路径输出，同时规定了运动副推导的串并联计算方法，并揭示了串并联计算法则与分析方式之间的内在联系。

(3) 将混联机构分为两类，建立了分形与混联机构的关系模型，实现了机构与分形理论在数理逻辑关系上的统一。

(4) 采用MATLAB编程的形式综合出3T三自由度混联机构，实现其中一个混联机器人机构的构型设计并验证了构型设法方法的正确性。

[1] 张曙,HeiselU. 并联运动机床[M]. 北京:机械工业出版社, 2003.ZHANGShu,HEISELU.ParallelKinematicsMachineTool[M].Beijing:ChinaMachinePress, 2003.

[2] 吴振勇, 王玉茹, 黄田.Tricept机器人的尺度综合方法研究[J]. 机械工程学报, 2003, 39(6):22-25.WUZhenyong,WANGYuru,HUANGTian.OptimalDimensionalSynthesisofTriceptRobot[J].JournalofMechanicalEngineering, 2003, 39(6):22-25.

[3] 李彬，黄田，刘海涛，等．Exechon混联机器人三自由度并联机构模块位置分析[J]. 中国机械工程, 2010, 21(23): 2785-2789.LIBin,HUANGTian,LIUHaitao,etal.PositionAnalysisofa3-DoFPKMModulefora5-DoFHybridRobotExechon[J].ChinaMechanicalEngineering, 2010, 21(23):2785-2789.

[4]OZGURE,DAHMOUCHER,ANDREFFN,etal.AVision-basedGenericDynamicModelofPKMsandItsExperimentalValidationontheQuattroParallelRobot[C]//IEEE/ASMEInternationalConferenceonAdvancedIntelligentMechatronics.Besancon, 2014:937-942.

[5] 吴孟丽，黄田，张大卫，等. 一种新型可重构装备TriVariant的概念设计[J].机械设计, 2004, 21(增1):28-30.WUMengli,HUANGTian,ZHANGDawei,etal.ResearchinSkillsofReconfigurableMachine-trivariant[J].JournalofMachineDesign, 2004, 21(Z1):28-30.

[6] 李秦川, 黄真. 基于位移子群分析的3自由度移动并联机构型综合[J]. 机械工程学报, 2003,39(6):18-21.LIQinchuan,HUANGZhen.TypeSynthesisfor3-DOFTranslationalParallelMechanismsBasedonDisplacementSubgroup[J].JournalofMechanicalEngineering, 2003, 39(6):18-21.

[7] 郭盛, 方跃法. 可实现空间取放作业的4自由度并联机器人机构综合[J]. 机器人, 2007, 29(5):417-422.GUOSheng,FANGYuefa.StructuralSynthesisfor4-DOFParallelManipulatorswithSpatialTakingandPuttingFunctions[J].Robot, 2007, 29(5):417-422.

[8] 杨廷力, 金琼, 刘安心,等. 基于单开链单元的三平移并联机器人机构型综合及分类[J]. 江苏石油化工学院学报, 2000, 12(4):35-38.YANGTingli,JINQiong,LIUAnxin,etal.StructuralSynthesisandClassificationofthe3DOFTranslationalParallelRobotMechanismsBasedontheUnitsofSingle-opened-chain[J].JournalofJiangsuInstituteofPetrochemicalTechnology, 2000, 12(4):35-38.

[9] 杨廷力, 金琼, 刘安心,等. 基于单开链单元的欠秩并联机器人机构型综合的一般方法[J]. 机械科学与技术, 2001, 20(3):321-325.YANGTingli,JINQiong,LIUAnxin,etal.AGeneralMethodforStructuralSynthesisoftheDegenerate-rankParallelRobotMechanismsBasedontheUnitsofSingle-opened-chain[J].MechanicalScienceandTechnology, 2001, 20(3):321-325.

[10]SHENHuiping,YANGTingli,MALüzhong.SynthesisandStructureAnalysisofKinematicStructuresof6-DoFParallelRoboticMechanisms[J].MechanismandMachineTheory, 2005, 40(10)：1164-1180.

[11] 沈惠平，赵海彬，邓嘉鸣，等. 基于自由度分配和方位特征集的混联机器人机型设计方法及应用[J]. 机械工程学报, 2011, 47(23)：56-64.SHENHuiping,ZHAOHaibin,DENGJiaming,etal.TypeDesignMethodandtheApplicationforHybridRobotBasedonFreedomDistributionandPositionandOrientationCharacteristicSet[J].JournalofMechanicalEngineering, 2011, 47(23)：56-64.

[12] 刘海涛, 黄田,CHETWYNDDG,等. 5自由度大工作空间/支链行程比混联机械手的概念设计与尺度综合[J]. 机械工程学报, 2007, 43(6):14-20.LIUHaitao,HUANGTian,CHETWYNDDG,etal.KinematicDesignof5-DOFHybridRobotwithLargeWorkspace/Limb-StrokeRatio[J].ChineseJournalofMechanicalEngineering, 2007, 43(6):14-20.

[13]GAOFeng,LIWeimin,ZHAOXianchao,etal.NewKinematicStructuresfor2-, 3-, 4-,and5-DOFParallelManipulatorDesigns[J].MechanismandMachineTheory, 2002, 37(11):1395-1411.

[14]GAOFeng,PENGBinbin,LIWeimin,etal.DesignofaNovel5DOFParallelKinematicMachineToolBasedonWorkspace[J].Robotica, 2005, 23(1): 35-43.

[15]KONGX,GOSSELINCM.TypeSynthesisof3DOFSphericalParallelManipulatorsBasedonScrewTheory[J].JournalofMechanicalDesign, 2004, 126(1)：523-531.

[16]KONGX,GOSSELINCM.TypeSynthesisof3T1R4-DOFParallelManipulatorsBasedonScrewTheory[J].IEEETransactionsonRobotics&Automation, 2004, 20(2)：181-190.

[17]KONGX,GOSSELINCM.TypeSynthesisof3-DOFTranslationalParallelManipulatorsBasedonScrewTheory[J].JournalofMechanicalDesign, 2004, 126(1)：83-92.

[18]KONGX,GOSSELINCM.TypeSynthesisof5-DOFParallelManipulatorsBasedonScrewTheory[J].JournalofRoboticSystems, 2005, 22(10)：535-547.

[19]HERVÉJM.TheLieGroupofRigidBodyDisplacements,aFundamentalToolforMechanismDesign[J].MechanismandMachineTheory, 1999, 34(5):719-730.

[20]GOGUG.StructuralSynthesisofFully-isotropicTranslationalParallelRobotsviaTheoryofLinearTransformations[J].EuropeanJournalofMechanicsA/Solids2004, 23(6):1021-1039.

[21]JUNGHK,CRANECD,ROBERTSRG.StiffnessMappingofCompliantParallelMechanismsinaSerialArrangement[J].MechanismandMachineTheory, 2008, 43(3)：271-284.

[22]BANDYOUPADHYAYS,GHOSALA.AnalyticalDeterminationofPrincipalTwistsinSerial,ParallelandHybridManipulatorsUsingDualVectorsandMatrices[J].MechanismandMachineTheory, 2004, 39(12)：1289-1305.

[23]CASTILLOO,MELINP.SoftComputingandFractalTheoryforIntelligentManufacturing(StudiesinFuzziness&SoftComputing)[M].Heidelberg:Physica-Verlag, 2003.

[24] 文志英. 分形几何的数学基础[M].上海：上海科技教育出版社,2000.WENZhiying.MathematicalFoundationsofFractalGeometry[M].Shanghai:ShanghaiScientificandTechnologicalEducationPublishingHouse, 2000.

[25] 曾强. 具有串并混联形式与变自由度特性的空间多环机构的拓扑设计方法[D]. 北京：北京交通大学, 2012.ZENGQiang.TopologicalDesignMethodsofSpatialMulti-loopMechanismswithSerial-parallelHybridFormsandKinematotropicProperties[D].Beijing：BeijingJiaotongUniversity, 2012.

[26]ZENGQ,FANGY.StructuralSynthesisofSerial-parallelHybridMechanismsBasedonRepresentationandOperationofLogicalMatrix[J].JournalofMechanisms&Robotics, 2009, 1(4)： 469-484.

[27]ZENGQ,FANGY.StructuralSynthesisofSerial-parallelHybridMechanismsviaGroupTheoryandRepresentationofLogicalMatrix[C]//InternationalConferenceonInformationandAutomation.Changsha, 2009：1392-1397.

[28] 廖明，刘安心，沈惠平，等. 面向计算机辅助分析的并联机构符号描述方法[J]. 农业机械学报, 2015, 46(7)：310-317.LIAOMing,LIUAnxin,SHENHuiping,etal.SymbolicDescriptionofParallelMechanismforComputerAidedAnalysis[J].TransactionoftheChineseSocietyforAgriculturalMachinery, 2015, 46(7)：310-317.

(编辑 陈 勇)

Type Synthesis of Three-translational Hybrid Mechanisms

GE Shuyi1,4CAO Yi1,2,3,4ZHOU Rui1,4ZHU Jingyuan1,4DING Zehua1,4

1. School of Mechanical Engineering, Jiangnan University, Wuxi, Jiangsu,214122 2. Key Laboratory of System Control and Information Processing, Shanghai, 200240 3. State Key Laboratory of Mechanical System and Vibration, Shanghai, 200240 4. Jiangsu Key Laboratory of Advanced Food Manufacturing Equipment and Technology, Wuxi, Jiangsu,214122

For a three translational hybrid mechanism with three degrees of freedom, an efficient synthesis methodology and a novel analysis approach were proposed from the view of fractal theory and topological graph. Firstly, the basic concept of the topology graph and the fractal theory were introduced. Secondly, the kinematic characteristics and algorithm were expounded. Thirdly, the model between the hybrid mechanism and fractal theory was established. And the procedure of methodology of type synthesis was concluded in detail, meanwhile, the three translational hybrid mechanism was synthesized. Finally, a method for analyzing the kinematic characteristics of hybrid mechanisms was proposed and applied to the synthesized structure by which the validity of the methodology proposed herein was demonstrated.

hybrid mechanism; type synthesis; fractal theory; 3 translation(3T)

2016-03-10

国家自然科学基金资助项目(50905075, 51505190)；江苏省“六大人才高峰”高层次人才项目(ZBZZ-012)；系统控制与信息处理教育部重点实验室开放课题资助项目(scip201506)；机械系统与振动国家重点实验室开放课题资助项目(MSV201407)

TH112DOI：10.3969/j.issn.1004-132X.2017.03.002

葛姝翌，女，1992年生。江南大学机械工程学院硕士研究生。主要研究方向为混联机构学理论及机器人技术。曹 毅(通信作者)，男，1974年生。江南大学机械工程学院教授、博士，上海交通大学系统控制与信息处理教育部重点实验室和上海交通大学机械系统与振动国家重点实验室访问学者。E-mail:caoyi@jiangnan.edu.cn。周 睿，女，1993年生。江南大学机械工程学院硕士研究生。朱景原，男，1991年生。江南大学机械工程学院硕士研究生。丁泽华，男，1993年生。江南大学机械工程学院硕士研究生。