基于ADMM字典学习的滚动轴承振动信号稀疏分解

孙占龙 佟庆彬

北京交通大学电气工程学院，北京，100044

基于ADMM字典学习的滚动轴承振动信号稀疏分解

孙占龙 佟庆彬

北京交通大学电气工程学院，北京，100044

在稀疏分解过程中，字典模型构建的结果会直接影响稀疏分解的效果。为获得结构更好的字典，提出了一种基于交替方向乘子法(ADMM)的字典学习方法，在字典学习过程中采用交替方向乘子法逐个更新字典中原子，得到的字典具有良好的结构。将该字典学习方法应用到滚动轴承振动信号稀疏分解中，能获得更快的字典学习速度和更好的稀疏分解效果。与K-SVD字典学习方法相比较，证明了所提方法在轴承信号稀疏分解中的优越性。

滚动轴承；稀疏分解；交替方向乘子法；字典学习

0 引言

滚动轴承大量应用于电机中，其工作状态会直接影响电机的运行状态。对滚动轴承的运行状态进行实时检测，可以及时发现轴承比较微弱的一些早期故障，避免对电机造成不必要的危害，减少人身财产损失。滚动轴承的运行状态诊断方法包括温度、油样分析、振动分析等，其中振动分析法最有效[1-2]。但是，在实际情况中，振动信号中包含大量的干扰，不利于进一步分解轴承故障信号。

为有效获取轴承故障的故障特征，MALLAT等[3]在总结前人研究成果的基础上，于1993年提出了信号在过完备字典上分解的思想。与传统的正交基变换不同，基于稀疏分解[4-6]方法的信号处理过程中，使用过完备字典能够得到信号的自适应表示，有利于信号特征的提取和识别。目前，过完备字典的构造方法有两种：传统的固定字典和经过学习构造的字典。传统的不经过学习的字典有Gabor字典、小波基字典、Chirplet字典等[7-11]，但是这类字典存在一个缺陷：字典是固定的，不能自适应地根据待分解信号进行变换。以K-SVD算法字典学习[12-13]为代表的字典学习方法有效地解决了这个问题，文献[12-13]将K-SVD算法应用于字典学习过程中，取得了良好的效果，它根据待分解信号对初始字典进行学习优化，在信号稀疏分解中有更好的效果。

K-SVD算法字典学习的过程中，每一次更新字典时都要通过SVD算法来进行处理，当字典的规模变得比较大时，使用SVD算法就会耗费比较长的时间，使整个算法变慢，这不利于对信号的实时处理。针对上述问题，本文在对交替方向乘子法(alternating direction method of multipliers，ADMM)[14-18]进行充分研究的基础上，将其应用于轴承信号稀疏分解的字典学习中。

1 基于ADMM字典学习的稀疏分解

1.1 ADMM

ADMM的概念早在20世纪70年代时已被提出，它在求解大规模稀疏分解问题的处理上十分有效，它通过增广拉格朗日函数构造将问题分裂为多个低维子问题进行迭代求解。利用ADMM将原问题的目标函数进行等价分离,并且分解为若干个较易找到局部解的子问题,从而得到原问题的全局解。ADMM的求解速度在稀疏分解中的优势十分明显,这也是其受到追捧的一个主要原因[14-15]。ADMM解决问题的一般形式如下：

(1)

式(1)的增广拉格朗日罚函数为

L(x,y,λ)=f(x)+g(y)+λT(Ax+By-b)+

(2)

其中，ρ是惩罚参数，ρ>0。经典ADMM的迭代步骤如下：

(3)

由式(3)可以看出，ADMM进行迭代的步骤包括一个x极小化、y极小化步骤和一个对偶变量迭代步骤，该算法先对x和y进行迭代更新，之后再对对偶变量λ进行迭代更新。ADMM对变量进行交替更新，这也就是其名字的来源，也可以认为是把Gauss-Seidel迭代应用于这两个变量中。在ADMM迭代框架中可以看出，该算法更适合解决变量可分离的问题，其目标函数也是可以分离的。

1.2 基于ADMM的字典学习

在滚动轴承振动信号稀疏分解过程中，构建一个结构良好的字典非常重要。固定的字典结构虽然冗余，但是其中原子未必贴合给定信号，不能根据信号自适应调整，根据待分解信号对初始字典进行学习，能更好地贴合待分解信号，包含更多的信号特征，在用于稀疏分解后，能得到更为稀疏的分解系数，获得比未学习字典更好的分解效果。

轴承信号稀疏分解过程中的字典学习可以表示为

(4)

i=1,2,…,L

其中，Y为训练矩阵；D为字典；X为信号在字典D上的投影系数；K为系数稀疏度的上界。

字典学习过程即式(4)的方法为变量交替更新法，其基本过程如下：首先利用给定的初始字典D和训练矩阵Y，用OMP算法进行稀疏编码，求解出系数X。然后，固定系数X，利用字典更新方法更新字典D。按照上述方法进行迭代，直到达到给定迭代次数或者达到给定的误差要求，即停止迭代，完成字典学习过程。

基于ADMM算法的字典学习过程中，首先将式(4)进行转换，令Z=DX，其格式为

(5)

则字典学习的拉格朗日函数为

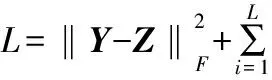
(6)

其中，Λ为拉格朗日乘子矩阵；Λi为Λ的第i列;〈〉表示内积运算。

将ADMM应用于式(6)中，并利用OMP算法进行系数的求解，最终获得字典的更新形式：

Dn+1(∶,i)=Dn(∶,i)+H(n)Xn(i,∶)T/(ω(n)+δ)

(7)

基于ADMM字典学习的基本过程如下：

(1)初始化。初始化字典D(0)，该矩阵既可以是随机分布的m×n矩阵，也可以从给定信号Y中选取n个长度为m的列向量。拉格朗日乘子矩阵为Λ(0)(一般为全1矩阵)，稀疏度为k,迭代次数为N,两个小的正数为α和β。

(2)主循环。根据给定的更新误差确定循环次数。

(3)稀疏分解。使用OMP算法求解系数矩阵X：

X=OMP(D,Y,k)

(8)

(4)更新字典。令

G(n)=(βD(n)X(n)+2Y-Λ(n))/(2+β)

(9)

H(n)=G(n)+Λ(n)/β-D(n)X(n)

(10)

(5)子循环。即

ω(n)=X(n)(∶,i)X(n)(∶,i)T

(11)

D(n+1)(∶,i)=D(n)(∶,i)+H(n)X(n)(i,∶)T/(ω(n)+δ)

(12)

子循环结束。

(6)将字典D作归一化处理，更新拉格朗日乘子矩阵。令

Λ(n+1)=Λ(n)+γβ(G(n)-D(n+1)X(n))

(13)

(7)若迭代达到规定次数或者满足信号重构的误差要求，则学习过程结束；否则，跳转到步骤(3)。

在字典学习过程中，参数β和矩阵Λ的选取对字典更新的收敛性有一定影响，在具体实验中，可以根据需要进行调整。

1.3 基于优化字典学习的稀疏分解

利用ADMM字典学习得到的过完备字典，对滚动轴承故障振动信号进行稀疏分解，基本步骤如下：

(1)获取滚动轴承故障振动信号，并根据给定的信号，选取训练矩阵和测试信号。

(2)利用ADMM字典学习方法对训练矩阵的特性进行学习，得到训练字典。

(3)根据学习得到的字典，利用OMP方法对测试信号进行稀疏分解和重构，得到去噪后的信号。

2 信号分析和验证

为了验证本文方法在轴承故障振动信号处理中的可行性，本文分别以仿真信号和轴承振动信号作为待处理信号，进行字典学习和稀疏分解，并通过学习结果和分解结果的对比，证明本文方法在信号稀疏分解中的优势。

本文以MATLAB 2014a作为信号处理平台，进行信号处理，并根据得到的结果绘制相应的图形，最后对得到的结果进行分析。

2.1 仿真信号分析

为了验证本文方法在字典学习中的有效性，本文首先采用随机信号进行字典学习和稀疏分解。

本实验中训练矩阵Y是随机生成的m×p矩阵，为保证字典学习的效果，取p=5m。随机生成大小为m×n的DCT矩阵作为初始矩阵D，其中n=2m，并对每一列进行归一化处理。为对比不同方法在字典学习中的表现，选取固定的迭代次数(本实验取10次)和相同的稀疏度(k=15)。

用本文方法和K-SVD字典学习方法分别进行字典学习，并记录两种方法在学习过程中所需要的时间。图1为字典行数从20增加到600时的学习所用时间,具体的运行时间见表1。

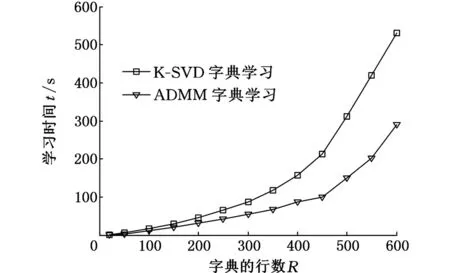
图1 字典学习时间比较Fig.1 Compare of dictionary learning time

s

从图1可以明显看出，在采用相同大小的测试矩阵、字典以及迭代次数的情况下，用本文方法所花费的时间比用K-SVD字典学习方法所花费的时间要少，而且随着字典规模的不断增大，这种优势越来越明显。当字典列数为600时，本文方法的学习时间约为K-SVD方法学习时间的1/2。

为了进一步验证本文方法在信号处理字典学习过程中的优越性,模拟以下仿真信号：

s(t)=2cos(2πft+5)

(14)

在该信号上加入标准正态分布的随机噪声，加噪后的信噪比SNR=-10dB。

从加噪信号中获取训练矩阵Y，产生DCT字典作为初始字典，进行字典学习。利用学习得到的字典，对原信号进行稀疏分解，获得重构信号的均方根误差(以下简称重构误差)：

(15)

其中，I是原始信号，In是重构信号，length(I)表示信号I的长度。取训练矩阵大小为100×300，字典大小为100×200，分解稀疏度为15，信号的重构误差随迭代次数增加的变化如图2所示。

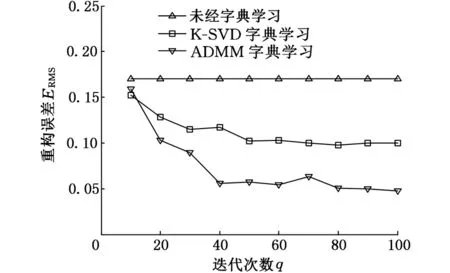
图2 重构误差随迭代次数的变化Fig.2 Changes of RMSE value with learning times

从图2可以看出，经过字典学习的重构信号的重构误差值明显小于未经学习的重构误差值，而且随着字典学习过程中迭代次数的增加，经过字典学习的重构信号的重构误差值逐渐减小。利用ADMM学习的信号重构误差值明显低于经K-SVD学习字典的重构误差值，而且随着迭代次数的增加，两者差距不断增大。但是当迭代次数大于80时，重构误差值趋于平稳，这表明信号分解的效果并不能随着字典学习迭代次数的增加而一直提高。从信号重构的重构误差值来看，经ADMM学习的字典明显优于K-SVD学习的字典。

2.2 轴承信号分析

为了验证本文方法在滚动轴承振动信号稀疏分解过程中的有效性，选择滚动轴承内圈故障信号为代表进行研究。

本文使用的实验数据来自美国凯斯西储大学轴承数据中心的滚动轴承振动数据[19]，滚动轴承为SKF6205-2RS型深沟球轴承，转速为1797 r/min，采样频率为12 kHz。实验中，根据重构的残余量和重构信号的包络谱，评价轴承信号稀疏分解的质量，并将本文方法与其他方法进行比较。

轴承内圈故障频率的计算公式为

(16)

其中，Z为滚动体个数，d为滚珠直径，D为节径，θ为压力角，f为轴转频。将轴承的各参数代入式(16)中，可以求得内圈故障频率约为164Hz。图3所示为轴承内圈故障振动信号。

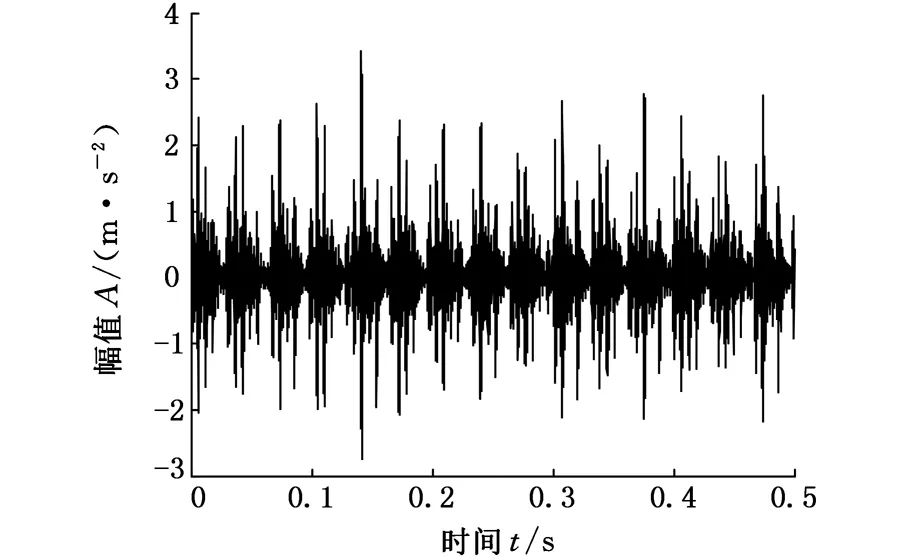
图3 轴承内圈故障振动信号Fig.3 Fault vibration signal of bearing inner ring

在本实验中，从轴承振动信号中截取长度为30 000的数据点，用来构造大小为100×200的训练矩阵，在剩余信号中截取1000点信号作为测试信号。构建DCT字典作为待学习字典，分别用K-SVD和ADMM两种方法进行字典学习。利用学习得到的字典，用OMP算法对测试信号进行稀疏分解和重构，获得信号重构的残余量，并对重构信号进行频谱分解，得到重构信号频谱图。

为对比不同方法的优劣，在选取相同的训练矩阵、初始字典和迭代次数的情况下，进行字典学习和测试信号的稀疏分解，获得重构信号的包络谱和重构残余量的大小。当字典学习次数为30、分解稀疏度为20时，得到信号重构残余量(图4)和重构信号包络谱图(图5)。

通过图4可以得到，在相同的迭代次数和稀疏度下，经过字典学习对轴承信号稀疏分解得到的重构残余量比未经过字典学习的稀疏分解的残余量小得多，其中本文方法的重构残余量比K-SVD字典学习方法的残余量小，这表明本文方法获得的字典更好地匹配了待分解的轴承信号，在稀疏分解和重构中有更好的表现。

图4 不同方法的重构残余量Fig.4 Residual volume of reconstruction of different methods

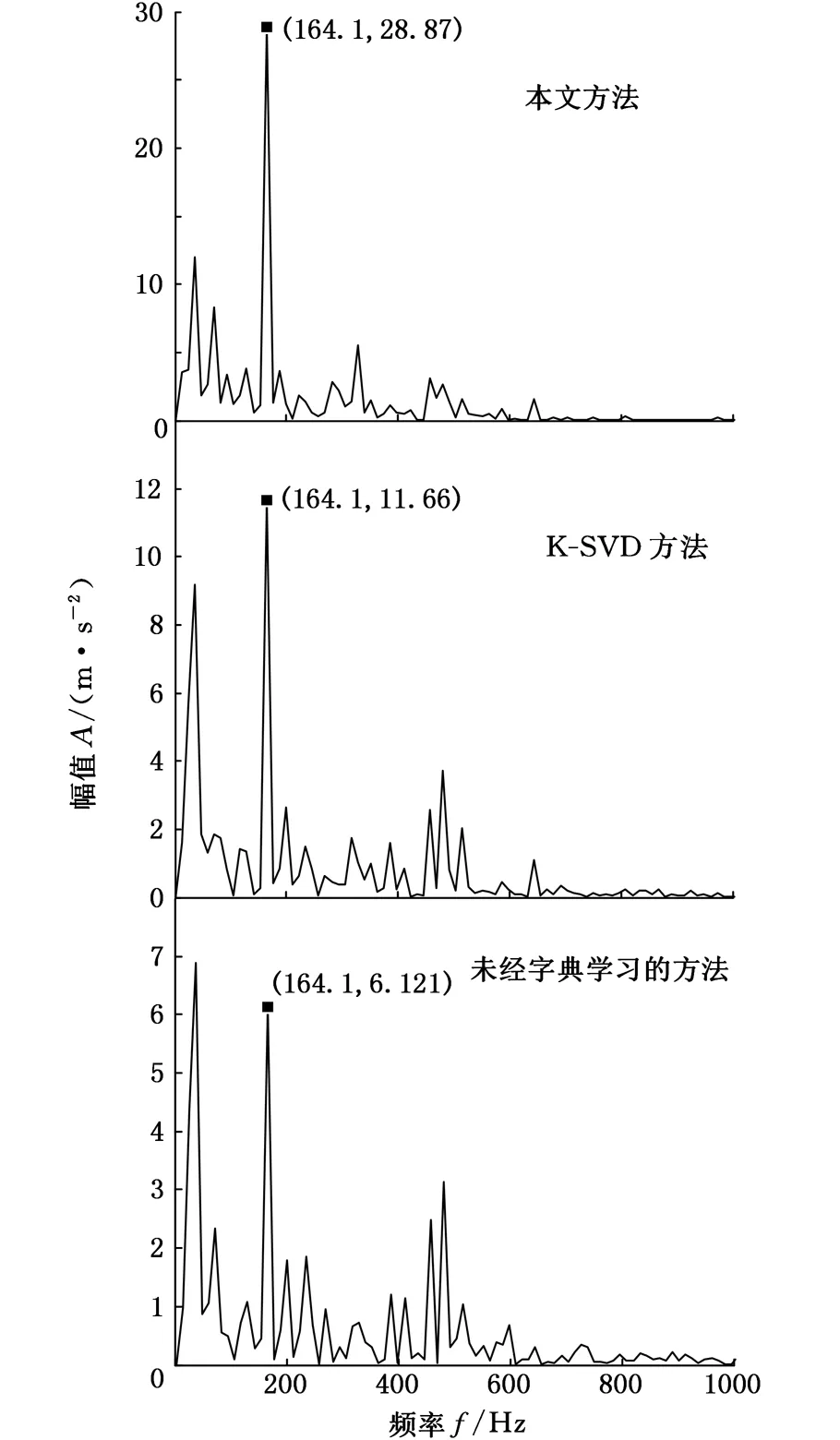
图5 信号稀疏分解得到的包络谱Fig.5 Envelope spectra obtained by spare decomposition

比较图5中三个包络谱图，可以明显看出，经过字典学习的分解效果比未经学习的效果好，包络谱中的故障频率更加明显，含有的干扰频率更少。同时，在相同的条件下，用两种方法学习获得的字典稀疏分解轴承故障信号，所得到的包络谱图也存在差别。在本文方法所获得的包络谱图中，轴承内圈故障频率fip十分明显，虽然存在一些干扰频率，但幅值小得多。而在K-SVD字典学习方法的包络谱图中，虽然可以识别出故障频率fip，但是个别干扰频率的幅值非常高。由此可得出，用本文方法学习得到的字典有更好的结构，更加符合待分解轴承信号的特征，在稀疏分解过程中能获得更好的分解效果。

3 结语

本文研究了基于ADMM的字典学习方法，并将该方法应用于滚动轴承信号的稀疏分解。以仿真信号和轴承内圈故障信号作为实验信号进行字典学习和稀疏分解，获得字典学习时间和稀疏分解结果。为验证本方法，取未经学习的字典和经K-SVD算法学习的字典作为对比对象，比较字典学习的速度和得到字典的结构。最后，比较了滚动轴承内圈故障振动信号的稀疏分解的效果。

和K-SVD算法一样，在基于ADMM的字典学习过程中，也容易陷入问题的局部最优点。为求得最优解，需要根据待分解信号的特征，对字典学习过程中参数进行相应的调整，如何对参数进行精确有效的调整还有待研究。

[1] 杨国安. 滚动轴承故障诊断实用技术[M]. 北京: 中国石化出版社, 2012:83-85.YANGGuoan.PracticalTechnologyofRollingBearingFaultDiagnosis[M].Beijing:ChinaPetrochemicalPress, 2012:83-85.

[2] 李辉, 郑海起, 唐力伟，等. 声测法和经验模态分解在轴承故障诊断中的应用[J].中国电机工程学报,2006,26(15):124-128.LIHui,ZHENGHaiqi,TANGLiwei,etal.ApplicationAcousticEmissionandEmpiricalModeDecompositiontoFaultsDiagnosisofBearing[J].ProceedingsoftheChineseSocirtyforElectricalEngineering, 2006, 26(15):124-128.

[3]MALLATSG,ZHANGZ.MatchingPursuitswithTime-frequencyDictionaries[J].IEEETransactionsonSignalProcessing,1993, 41(12): 3397-3415.

[4] 史丽丽.基于稀疏分解的信号去噪方法研究[D]. 哈尔滨：哈尔滨工业大学,2013.SHILili.ResearchonSignalDenoisingMethodBasedonSparseDecomposition[D].Harbin：HarbinInstituteofTechnology,2013.

[5] 陈向民,于德介,罗洁思，等.基于信号共振稀疏分解的转子早期碰摩故障诊断方法[J].中国机械工程,2013,24(1):35-41.CHENXiangmin,YUDejie,LUOJiesi,etal.EarlyRub-impactDiagnosisofRotorsbyUsingResonance-basedSparseSignalDecomposition[J].ChinaMechanicalEngineering,2013,24(1):35-41.

[6] 张晗,杜朝辉,方作为，等.基于稀疏分解理论的航空发动机轴承故障诊断[J].机械工程学报,2015,51(1):97-105.ZHANGHan,DUZhaohui,FANGZuowei,etal.SparseDecompositionBasedAero-engine’sBearingFaultDiagnosis[J].JournalofMechanicalEngineering,2015,51(1):97-105.

[7] 康晨晖，崔玲丽，王婧，等．基于信号特征的复合字典多原子匹配算法研究[J].机械工程学报，2012,48 (12)：1-6.KANGChenhui,CUILingli,WANGJing,etal.ResearchontheCompositeDictionaryMulti-atomsMatchingAlgorithmBasedontheSignalCharacter[J].JournalofMechanicalEngineering,2012,48(12):1-6.

[8] 郭金库, 吴瑾颖, 张茜，等. 基于稀疏分解的多分量线性调频信号参数估计[J].振动与冲击,2011, 30(1):175-179.GUOJinku,WUJinying,ZHANGQian,etal.MulticomponentChirpSignalParameterEstimationviaSparseRepresentation[J].JournalofVibrationandShock,2011,30(1):175-179.

[9]GRIBONVALR.FastMatchingPursuitwithaMultiscaleDictionaryofGaussianChirps[J].IEEETransactiononSignalProcessing,2001,49(5):994-1001.

[10] 梁锐华, 成礼智. 基于小波域字典学习方法的图像双重稀疏表示[J]. 国防科技大学学报,2012,34(4):126-131.LIANGRuihua,CHENGLizhi.DoubleSparseImageRepresentationviaLearningDictionariesinWaveletDomain[J].JournalofNationalUniversityofDefenseTechnology,2012,34(4):126-131.

[11]VERA-CANDEASP,RUIZ-REYESN,ROSA-ZURERAM,etal.TransientModelingbyMatchingPursuitswithaWaveletDictionaryforParametricAudioCoding[J].IEEESignalProcessingLetters,2004,11(3):349-352.

[12] 翟雪含, 朱卫平, 康彬，等. 结合KSVD和分类稀疏表示的图像压缩感知[J]. 计算机工程与应用,2015, 51(6): 193-198.ZHAIXuehan,ZHUWeiping,KANGBin,etal.CompressedSensingofImagesCombiningKSVDandClssifiedSparseRepresentation[J].ComputerEngineeringandApplications,2015,51(6):193-198.

[13]AHARONM,ELADM,BRUCKSTEINA,etal.K-SVD:AnAlgorithmforDesigningoverCompleteDictionariesforSparseRepresentation[J].IEEETransactionsonSignalProcessing,2006,54(11):4311-4322.

[14] 李玉胜. 交替方向法及其应用[D].合肥:中国科学技术大学, 2015.LIYusheng.AlternatingDirectionMethodandItsApplication[D].Hefei:UniversityofScienceandTechnologyofChina,2015.

[15] 钟轶君. 范数最优化问题的交替方向乘子算法[D]. 大连: 大连理工大学,2013.ZHONGYijun.NormOptimizationviaAlternationDirectionMethodofMultipliers[D].Dalian:DalianUniversityofTechnology,2013.

[16]BOYDS,PARIKHN,CHUE,etal.DistributedOptimizationandStatisticalLearningviatheAlternatingDirectionMethodofMultipliers[J].FoundationsandTrendsinMachineLearning,2011,3(1):1-122.

[17] 李佩杰, 陆镛, 白晓清，等.基于交替方向乘子法的动态经济调度分散式优化[J]. 中国电机工程学报,2015,35(10):2428-2435.LIPeijie,LUYong,BAIXiaoqing,etal.DecentralizedOptimizationforDynamicEconomicDispatchBasedonAlternatingDirectionMethodofMultipliers[J].ProceedingsoftheChineseSocietyforElectricalEngineering,2015,35(10):2428-2435.

[18]ERSEGHET.DistributedOptimalPowerFlowUsingADMM[J].IEEETransactionsonPowerSystems:aPublicationofthePowerEngineeringSociety,2014,29(5):2370-2380.

[19]CaseWesternReserveUniversityBearingDataCenter[EB/OL].Cleveland:CaseWesternReserveUniversity[2013-05-01]http://csegroups.case.edu/bearingdatacenter/pages/download-data-file,2013.

(编辑 陈 勇)

Sparse Decomposition of Vibration Signals of Rolling Bearings Based on ADMM Dictionary Learning

SUN Zhanlong TONG Qingbin

School of Electrical Engineering ,Beijing Jiaotong University,Beijing,100044

In the processes of sparse decomposition, the effects of sparse decomposition would be directly affected by dictionary model construction.A dictionary learning method was proposed based on ADMM herein. In the processes of dictionary learning, the ADMM was used to update the atoms in the dictionary, which might obtain the dictionary with better structure. The method was applied to the sparse decomposition of the vibration signals of rolling bearings, shorter dictionary learning time and better sparse decomposition results might be obtained. Compared with the K-SVD dictionary learning method, the proposed method has the superiority in the sparse decomposition of bearing signals.

rolling bearing;sparse decomposition;alternating direction multiplier method (ADMM);dictionary learning

2016-03-25

TH113.1；TH165.3

10.3969/j.issn.1004-132X.2017.03.010

孙占龙，男，1991年生。北京交通大学电气工程学院硕士研究生。主要研究方向为故障诊断、损伤评估及寿命预测技术。佟庆彬(通信作者)，男，1979年生。北京交通大学电气工程学院副教授。E-mail:tqbin818@126.com。