基于双树复小波和自适应权重和时间因子的粒子群优化支持向量机的轴承故障诊断

张淑清 胡永涛 姜安琦 吴 迪 陆 超 姜万录

1.燕山大学电气工程学院,秦皇岛，0660042.中南大学信息科学与工程学院，长沙，4100063.燕山大学机械工程学院，秦皇岛，066004

基于双树复小波和自适应权重和时间因子的粒子群优化支持向量机的轴承故障诊断

张淑清1胡永涛1姜安琦2吴 迪1陆 超1姜万录3

1.燕山大学电气工程学院,秦皇岛，0660042.中南大学信息科学与工程学院，长沙，4100063.燕山大学机械工程学院，秦皇岛，066004

提出了一种基于双树复小波和具有自适应权重和时间因子的粒子群算法优化支持向量机的轴承故障诊断方法。首先对机械振动信号进行DTCWT变换，提取能量熵作为特征向量。然后采用AWTFPSO算法优化SVM，实现轴承故障诊断。不同方法的对比实验及分析结果表明，该方法速度快、准确率高。

双树复小波；支持向量机；粒子群算法；自适应权重和时间因子；故障诊断

0 引言

机械故障诊断技术是保证生产系统安全稳定运行和提高产品质量的重要手段和关键技术，其研究的关键在于信号特征提取和模式识别。常用的特征提取方法有傅里叶变换[1]、小波变换[2]和S变换[3]等，主要的分类器有神经网络[4]、支持向量机[5]和贝叶斯分类器[6]等。小波变换大量成功应用于信号特征提取[7]，但实小波变换存在平移敏感性、方向性差、相位信息缺乏等缺点。复小波变换因其优异的特性，能以较小代价同时克服实小波变换的多个缺点，逐渐成为信号处理领域的研究热点[8]。 双树复小波(dual-tree complex wavelet transform，DTCWT)具有一般复小波的优良特性，并且采用双树结构保证信号完整重构，同时具有平移不变性、方向选择性、抑制频率混叠、有限冗余度和高效计算能力[9]。机械振动信号中含有大量扰动信号，这些扰动可导致局部信号的微小平移，而DTCWT平移不变性的优点减小了扰动信号在分解重构过程畸变的影响，因此，将DTCWT用于机械振动信号分析，采用DTCWT进行特征提取可以取得良好的效果。

机械故障模式识别属于典型的小样本识别问题[10]，支持向量机(support vector machines,SVM)在解决小样本识别问题方面有突出优点[11]，被广泛用于模式识别中。然而，SVM的分类性能取决于惩罚系数和核函数参数，目前尚无统一的理论或标准用于SVM参数选取，一般通过经验选择或采用交叉验证法，但经验不足就得不到最优参数。而交叉验证法耗时长、计算量大，所得参数不一定是最优参数。随着人工智能研究的深入，将一些智能算法用于SVM参数优化的方法得到了广泛关注[12]，常用的有遗传算法(genetic algorithm, GA)[13]和粒子群(particle swarm optimization, PSO)算法[14]。PSO算法采用“速度-位移”的模型，没有GA的“交叉”和“变异”操作，比遗传算法规则更简单，有利于工程实现。此外，PSO算法特有的记忆功能保证每个个体都能跟踪当前群体的搜索情况，动态调整搜索机制，具有对多峰值的并发搜索能力[15]。

PSO算法参数选取不当会导致算法收敛速度慢或者陷入局部最优[16]，针对此问题，本文对PSO算法局部搜索和全局搜索能力进行深入研究，在PSO算法中加入自适应权重和时间因子，提出具有自适应权重和时间因子的粒子群(adaptive weighting and time factor particle swarm optimization,AWTFPSO)算法，该算法根据适应度自适应调整局部搜索和全局搜索能力，能有效克服PSO算法的缺点。

1 DTCWT能量熵

DTCWT是一种改进的复小波变换，DTCWT采用两棵并列的具有不同高通和低通滤波器组的实小波变换(DWT)树实现，分别称为实树和虚树，两棵实小波变换树满足完美重构条件。

设两路实小波分别为ψh(t)和ψg(t)，将一路实小波变换为复数域，得双树复小波：

ψC(t)=ψh(t)+jψg(t)

(1)

(2)

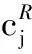
(3)

i=1,2,…,j

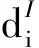
(4)

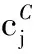
(5)

在第一层分解时实树和虚树滤波器组之间的延迟恰好是一个采样值的间隔，因此，双树二抽取得到的数据形成互补关系，即实树抽取到的数据正好是虚树树未抽取到的，减少了信息的丢失，从而使ψC(t)近似解析，获得近似平移不变性，减小了信号中平移扰动的影响。

为了验证DTCWT的平移不变性，对相邻信号平移一个采样位置的16个单位阶跃信号进行分析，如图1所示。

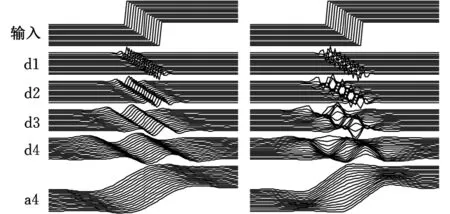
(a)双树复小波变换(DTCWT) (b)实小波变换(DWT)图1 双树复小波平移不变性Fig.1 Shift-invariance of DTCWT

图1中，d1～d4和a4分别为各尺度重构信号，图1a为DTCWT分解重构结果，当信号有平移时，DTCWT变换结果也有类似的平移，重构信号的形状和幅值并没有发生明显变化，即DTCWT具有很好的平移不变性。图1b为DWT分解重构结果，可以看出重构信号的形状和幅值发生了显著变化，出现了振荡。由此可知，在分析信号时如果在时域对信号做过平移或者原始信号中本身含有平移扰动成分，则可能会打破DWT变换的平衡而使DWT变换的结果不准确，但DTCWT避免了这一问题，从而使分析结果更准确。

熵是机械故障特征提取中最常用的方法，包含信号在动态变化中潜在的有用信息，熵值大小反映了信号概率分布的均匀程度。相对于能量，熵值具有一定抗噪能力，具有一定的鲁棒性，不同的轴承故障信号的能量不同，因此，采用能量熵作为轴承故障的特征。首先，对每个电能质量扰动信号样本进行n层DTCWT分解，重构得到n+1个不同频带的分量。然后，计算每个分量每个采样点的能量Ei，根据下式分别计算每个分量的能量熵H:

(6)

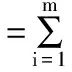
即可得到n+1维特征向量。其中，k可取2或其他值；εi为每个采样点的能量占该频带总能量的比重；m为每个频带的采样点数。

2 AWTFPSO算法

PSO算法是通过迭代找到最优解，在每一次迭代中，粒子通过跟踪个体极值pbest(粒子本身的最优解)和全局极值gbest(整个种群最优解)来更新自己[17]，粒子在找到这两个极值后，根据下式分别更新自己的速度与位置：

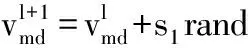
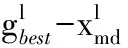
(7)

(8)

m=1,2,…,n1≤d≤Dl≥0式中，n为粒子个数；D为空间维数；l为当前迭代次数；s1、s2为学习因子，分别代表局部搜索能力和全局搜索能力；rand()为[0,1]之间的随机值，以体现算法的随机性。

式(7)是对粒子速度的更新，其等号右边第一项是粒子当前速度，后两项是对粒子速度的调整，保证粒子群具有全局搜索能力和局部搜索能力[18]。较大的速度有助于全局搜索，但是会降低收敛速度，如果速度过大则会丢失最优解，较小的速度有利于局部搜索，加快收敛速度；但是速度过小容易陷入局部最优，速度的调整成为PSO算法的瓶颈，因此，在式(7)中引入惯性权重，得

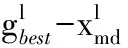
(9)

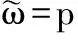
(10)

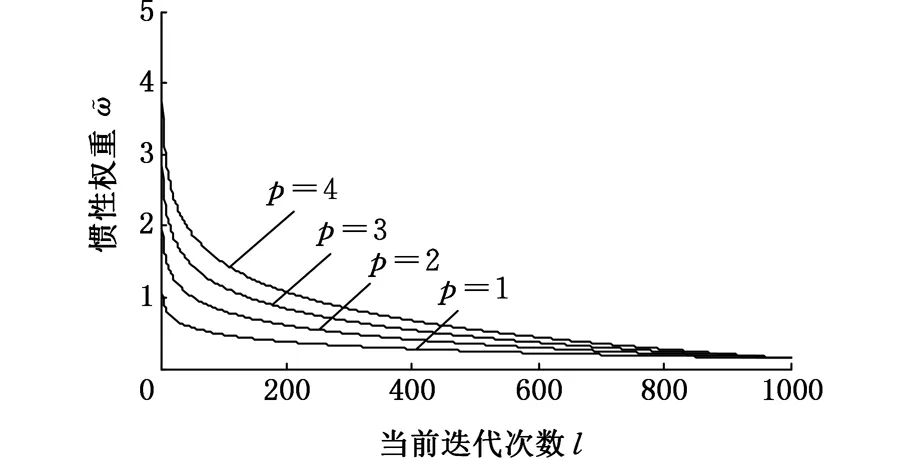
图2 p值不同时和l的关系Fig.2 Relationship between and l with different p

式(8)是对粒子位置的更新，即在原始位置加上变异速度。物理上只有量纲相同的物理量之间才可以相互运算，同时为了改善粒子群性能，在式(8)中增加自适应时间因子Al，即

(11)

当Al=1时，式(11)变为式(8)；当Al≠1时，粒子群开始时选择较大的Al以利于全局搜索；迭代到一定程度时，选择较小的Al以利于局部搜索，采用神经网络中的Sigmoid函数来构造非线性递减时间因子：

Al=1-2/(2+e-15(αl-0.5))

(12)

其中，αl为粒子群多样性指标，用来描述粒子的分散程度：

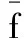
(13)

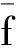
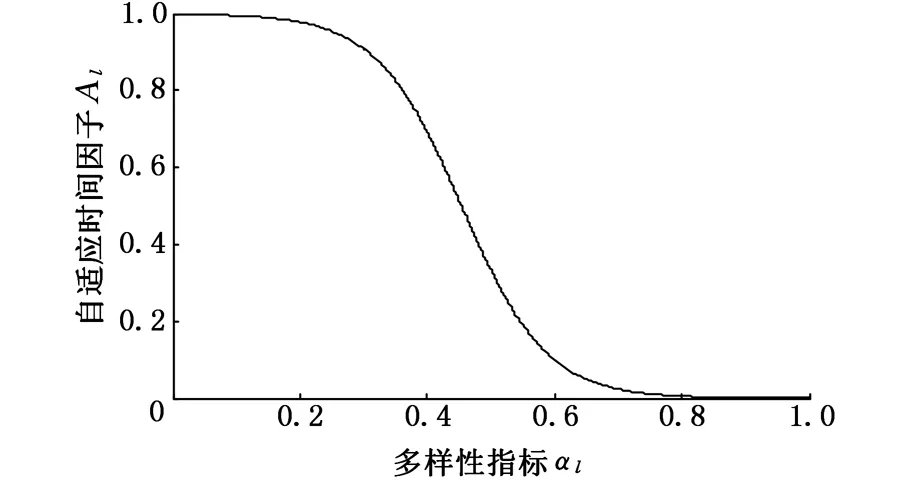
图3 Al和αl的变化关系Fig.3 Change relation of Al and αl

综上所述，AWTFPSO算法能有效控制粒子的飞行速度和搜索范围，自适应地调整局部搜索能力和全局搜索能力，进而加快收敛速度，同时避免陷入局部最优，采用AWTFPSO算法优化SVM即可实现参数自动选取，得到最优参数。

3 AWTFPSO算法优化SVM

SVM分类器的主要思想是通过非线性映射函数把数据样本映射到高维特征空间，再在高维特征空间中求得最优分类面来分离训练样本点，使得训练样本点与最优分类面距离最大化[19]，其最核心的问题是参数优化问题，AWTFPSO算法可以很好地解决SVM参数优化问题。

设定SVM训练样本集如下：

D={(xu,yu),u=1,2,…,v}

(14)

其中，xu∈Rn为输入向量，yu∈{+1,-1}为输出向量,v为样本数。延伸到多维空间时，求解最优分类面的问题转化为以下求解对偶二次优化问题：

(15)

式中，αi为拉格朗日乘子；q为惩罚系数；s(xu,xr)为核函数。

惩罚系数的作用是在确定特征子空间时调节学习机器置信区间的范围，即在确定的特征子空间中调节学习机器置信范围和经验风险的比例，以使学习机器的推广能力达到最优。q值越小表示对经验误差的惩罚越小，经验风险值越大，反之亦然。当q趋于无穷大时，表示所有的约束条件都必须满足，这意味着训练样本必须准确地分类，每个特征子空间至少存在一个合理的q值，使得SVM推广能力达到最佳。

求解式(15)得到对应的分类决策函数：

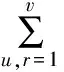
(16)

常用的核函数有径向基函数、多项式函数、Sigmoid函数[20-21]。本文采用径向基函数作为核函数，径向基函数如下：

s(xu,xr)=exp(-‖xu-xr‖/(2σ2))

(17)

其中，σ为径向基半径，是一个自由参数。当σ过大时，SVM对训练样本的错误率为零，但是对新样本的正确分类率也比较低，即推广识别率较低，其分类能力较差；当σ过小时，SVM只能得到一个接近于常数的判别函数，因此，对样本的正确分类率也很低，并且推广能力差，会出现“过度拟合”的现象，因而降低了对新样本的正确分类能力。

根据式(15)和式(17)，本文需要优化的参数为惩罚系数q和核函数系数σ，采用AWTFPSO对SVM参数进行优化，具体步骤如下：

(1)初始化粒子群，随机产生粒子的位置和速度。设置粒子群大小为20，进化代数为30。

(2)用初始值训练SVM。

(3)计算粒子当前最优适应度和平均适应度，适应度为SVM分类准确率，即采用交叉验证的方法，将原数据分成N组，每组分别作为一次测试集，同时其余N-1组作为训练集，得到N个模型，用N个模型的测试集的分类准确率平均值作为分类器的性能指标。

(5)根据式(3)和式(5)分别更新当前粒子的位置和速度。

(6)当迭代次数或适应度满足终止条件，终止迭代，得到优化参数，否则跳到步骤(2)。

4 实验分析

为了验证本文方法的有效性和优越性，采用不同的特征提取方法并与常用PSO和GA优化的SVM进行性能对比。实验数据采用美国华盛顿凯斯西储大学电气工程实验室的滚动轴承数据，本文研究正常状态(n)、内圈不同程度损伤(ir007，ir014，ir021)、滚动体不同程度损伤(b007，b014，b021)和外圈不同程度损伤(or007，or014，or021)共十种状态，每种状态取30组数据，每组1280数据点，得到十个30×1280的数组，电机转速为1750r/min，负荷为1.47kW，采样频率为12kHz。

对十种状态的每组数据进行DTCWT五层分解并进行单支重构，得到6个频带的分量，以正常状态振动信号为例，各频带分量如图4所示，可以看出DTCWT能有效提取信号各频段信息。计算每个分量的能量熵作为特征向量，十种状态得到300×6的特征向量，以a5分量为例，十种状态的能量熵如图5所示，由图5可以判断出正常状态和故障状态，但是br007、br014、br021和b014四种故障之间相互重叠，不能直观地判断，因此，采用SVM进行分类识别。

图4 正常信号DTCWT五层分解各频带分量Fig.4 Each frequency bands component of normal signal decomposed by 5 level DTCWT

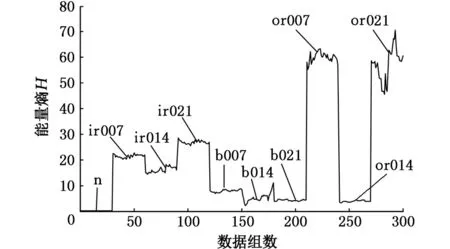
图5 a5分量十种状态的能量熵Fig.5 Energy entropy of a5 component of ten states

采用AWTFPSO算法优化SVM，将特征向量作为训练集输入AWTFPSO算法优化的SVM进行分类识别，进化代数为30，以5折交叉验证分类准确率作为算法适应度。同时分别采用PSO算法和GA优化SVM作为对比。图6所示为DTCWT熵作为特征时各算法适应度曲线，表1为采用DTCWT熵作为特征时各算法得到的最优参数q和σ2及最终的分类准确率。由图6和表1可以看出，AWTFPSO算法优化的SVM识别准确率在第4代达到100%，而PSO算法优化的SVM识别准确率在第28代达到最高值99.9%，GA优化的SVM识别准确率在第11代达到最高值99.6%，可见AWTFPSO算法优化的SVM在收敛速度和识别准确率上得到了较大提高。

图6 DTCWT能量熵作为特征时各算法适应度曲线Fig.6 Fitness curves of different algorithms when DTCWT energy entropy taken as feature

优化算法惩罚系数q核函数系数σ2分类准确率(%)AWTFPSO1．820．10100PSO9．230．8799．90GA5．403．1899．60

为了进一步验证本文方法的快速性、准确性，采用不同的特征DWT能量熵和EMD能量熵进行对比。图7所示为采用DWT能量熵作为特征时各算法适应度曲线，表2为采用DWT能量熵作为特征时各算法得到的最优参数q和σ2及最终分类准确率。由图7和表2可以看出，采用DWT

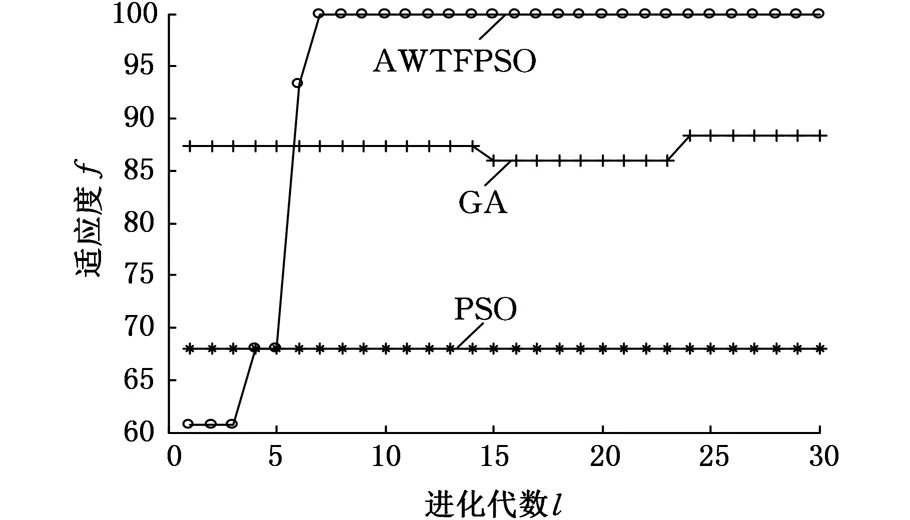
图7 DWT能量熵作为特征时各算法适应度曲线Fig.7 Fitness curves of different algorithms when DWT energy entropy taken as feature

优化算法惩罚系数q核函数系数σ2分类准确率(%)AWTFPSO2．270．10100PSO17．9934．3968GA14．685．4888．33

能量熵作为特征向量时AWTFPSO算法优化的SVM识别准确率在第7代达到100%，而PSO算法和GA优化的SVM最终识别准确率分别为68%和88.33%，陷入了局部最小，表明AWTFPSO算法优化的SVM能有效避免陷入局部最小。

图8所示为采用EMD能量熵作为特征时各算法适应度曲线，表3为采用EMD能量熵作为特征时各算法得到的最优参数q和σ2及最终分类准确率。由图8和表3可以看出，采用EMD能量熵作为特征向量时,AWTFPSO算法优化的SVM识别准确率在第4代达到100%，而PSO算法优化的SVM识别准确率在第21代达到最高值96%，GA优化的SVM识别准确率在第28代达到最高值100%，表明AWTFPSO算法优化的SVM在收敛速度和识别准确率上优于采用其他算法优化的SVM。

图8 EMD能量熵作为特征时各算法适应度曲线Fig.8 Fitness curves of different algorithms when EMD energy entropy taken as feature

优化算法惩罚系数q核函数系数σ2分类准确率(%)AWTFPSO6．580．10100PSO4．181．6096GA15．630．22100

对比图6～图8，对不同的特征提取方法进行比较，采用DTCWT能量熵作为特征时，AWTFPSO算法优化的SVM 在收敛速度上优于DWT，而在初始分类准确率上明显高于DWT和EMD；PSO优化的SVM虽然收敛速度慢，但分类准确率最高；GA优化的SVM在收敛速度上明显优于DWT和EMD。综上分析，DTCWT能更好地对机械振动信号进行分解重构，提取有效特征，AWTFPSO优化的SVM在分类中能有效避免陷入局部最小，具有较快的收敛速度及较高的分类准确率。将DTCWT能量熵与AWTFPSO优化的SVM相结合，能够快速准确地识别轴承故障。

5 结论

(1) DTCWT具有平移不变性，能有效避免扰动信号的影响，较好地对机械振动信号进行分解和重构，DTCWT能量熵能很好地表征机械振动信号的特征。

(2)AWTFPSO算法在PSO算法中加入自适应惯性权重和时间因子，能根据适应度自动调节局部搜索和全局搜索能力，克服PSO算法因参数选取不当导致收敛速度慢和易陷入局部最优的缺点。采用AWTFPSO算法优化SVM，解决了SVM参数选取问题，提高了SVM分类识别的速度和准确率。

(3)将DTCWT能量熵与AWTFPSO优化的SVM相结合用于机械故障诊断具有准确快速的优点，为机械故障诊断提供了一种新方法。

[1] 唐先广, 郭瑜, 丁彦春, 等. 基于短时傅里叶变换和独立分量分析的滚动轴承包络分析[J]. 机械强度, 2012, 34(1)：1-5. TANG Guangxian, GUO Yu, DING Yanchun, et al. Application of Rolling Element Bearing Envelope Analysis Based on Short Time Fourier Transition and Independent Components Analysis[J]. Journal of Mechanical Strength, 2012, 34(1):1-5.

[2] 杨绍普, 赵志宏. 改进的小波相邻系数降噪方法及其在机械故障诊断中的应用[J].机械工程学报, 2013, 49(17)：137-141. YANG Shaopu, ZHAO Zhihong. Improved Wavelet Denoising Using Neighboring Coefficients and Its Applitcation to Machinery Fault Diagnosis[J]. Journal of Mechanical Engineering,2013, 49(17):137-141.

[3] 张云强, 张培林, 吴定海, 等. 基于最优广义 S 变换和脉冲耦合神经网络的轴承故障诊断[J]. 振动与冲击, 2015, 34(9)：26-31. ZHANG Yunqiang, ZHANG Peilin, WU Dinghai, et al. Bearing Fault Diagnosis Based on Optimal Generalized S Transform and Pulse Coupled Neural Network[J]. Journal of Vibration and Shock, 2015, 34(9):26-31.

[4] Bin G F, Gao J J, Li X J, et al. Early Fault Diagnosis of Rotating Machinery Based on Wavelet Packets—Empirical Mode Decomposition Feature Extraction and Neural Network[J]. Mechanical Systems and Signal Processing, 2012, 27(2):696-711.

[5] 郑近德, 程军圣, 杨宇. 多尺度排列熵及其在滚动轴承故障诊断中的应用[J]. 中国机械工程, 2013, 24(19)： 2641-2646. ZHENG Jinde, CHENG Junsheng, YANG Yu.Multi-scale Permutation Entropy and Its Applications to Rolling Bearing Fault Diagnosis[J]. China Mechanical Engineering, 2013, 24(19): 2641-2646.

[6] 秦大力, 于德介. 基于本体的机械故障诊断贝叶斯网络[J]. 中国机械工程, 2013, 24(9): 1195-1209. QIN Dali, YU Dejie.Ontology-based Diagnostic Bayesian Networks for Mechanical Fault Diagnosis[J]. China Mechanical Engineering, 2013, 24(9): 1195-1209.

[7] DEMIREL H, ANBARJAFARI G. Image Resolution Enhancement by Using Discrete and Stationary Wavelet Decomposition[J]. Image Processing, IEEE Transactions on, 2011, 20(5):1458-1460.

[8] 艾树峰. 基于双树复小波变换的轴承故障诊断研究[J]. 中国机械工程, 2011, 22(20)：2446-2451. AI Shufeng. Research on Bearing Fault Diagnosis Based on Dual-tree Complex Wavelet Transform[J]. China Mechanical Engineering, 2011, 22(20): 2446-2451.

[9] 胥永刚, 孟志鹏, 陆明, 等. 双树复小波和奇异差分谱在滚动轴承故障诊断中的应用[J]. 振动工程学报, 2013, 26(6)：965-973. XU Yonggang, MENG Zhipeng, LU Ming, et al. Application of Dual-tree Complex Wavelet Transform and Singular Value Difference Spectrum in the Rolling Bearing Fault Diagnosis[J]. Journal of Vibration Engineering, 2013, 26(6):965-973.

[10] 王国彪, 何正嘉, 陈雪峰, 等. 机械故障诊断基础研究 “何去何从”[J]. 机械工程学报, 2013, 49(1)：63-72. WANG Guobiao, HE Zhengjia, CHEN Xuefeng, et al. Basic Research on Machinery Fault Diagnosis-What is the Prescription[J]. Journal of Mechanical Engineering, 2013, 49(1):63-72.

[11] 李鑫滨, 陈云强, 张淑清. 基于改进 ABC 算法优化的 LSSVM 多分类器组机械故障诊断模型[J]. 中国机械工程, 2013, 24(16): 2157-2164. LI Xinbin, CHEN Yunqiang, ZHANG Shuqing.Mechanical Fault Diagnosis Model Based on Improved ABC Algorithm Optimized Multiple LSSVM Classifier Group[J]. China Mechanical Engineering, 2013, 24(16): 2157-2164.

[12] TIAN J, HU Q, MA X, et al. An Improved KPCA/GA-SVM Classification Model for Plant Leaf Disease Recognition[J].Journal of Computational Information Systems, 2012, 8(18)：7737-7745.

[13] HARISH N, LOKESH A, MANDAL S, et al. Parameter Optimization Using GA in SVM to Predict Damage Level of Non-reshaped Berm Breakwater[J]. The International Journal of Ocean and Climate Systems, 2014, 5(2)：79-88.

[14] SUBASI A. Classification of EMG Signals Using PSO Optimized SVM for Diagnosis of Neuromuscular Disorders[J]. Computers in Biology and Medicine, 2013, 43(5)：576-586.

[15] XUE Z, DU P, SU H. Harmonic Analysis for Hyperspectral Image Classification Integrated with PSO Optimized SVM[J]. Selected Topics in Applied Earth Observations and Remote Sensing, IEEE Journal of, 2014, 7(6)：2131-2146.

[16] 匡芳君, 徐蔚鸿, 张思扬. 基于改进混沌粒子群的混合核 SVM 参数优化及应用[J]. 计算机应用研究, 2014, 31(3)：671-674. KUANG Fangjun, XU Weihong, ZHANG Siyang. Parameter Optimization and Application of SVM with Mixtures Kernels Based on Improved Chaotic Particle Swarm Optimization[J]. Application Research of Computers, 2014, 31(3):671-674.

[17] SHAKIBA R, SALEHI M E. PSO-based Path Planning Algorithm for Humanoid Robots Considering Safety[J]. Journal of Computer & Robotics, 2014, 5(1)：47-54.

[18] 马国庆, 李瑞峰, 刘丽. 学习因子和时间因子随权重调整的粒子群算法[J]. 计算机应用研究, 2014, 31(11)：3291-3294. MA Guoqing, LI Ruifeng,LIU Li. Particle Swarm Optimization Algorithm of Learning Factors and Time Factor Adjusting to Weights[J]. Application Research of Computers, 2014, 31(11)：3291-3294.

[19] DANENAS P, GARSVA G. Selection of Support Vector Machines Based Classifiers for Credit Risk Domain[J]. Expert Systems with Applications,2015, 42(6): 3194-3204.

[20] 田中大, 高宪文, 石彤，等. 用于混沌时间序列预测的组合核函数最小二乘支持向量机[J].物理学报, 2014, 63(16)：66-76. TIAN Zhongda, GAO Xianwen, SHI Tong,et al. Combination Kernel Function Least Squares Support Vector Machine for Chaotic Time Series Prediction[J]. Acta Physica Sinica, 2014,63(16): 66-76.

[21] HSUC W, LIN C J. A Comparison of Methods for Multiclass Support Vector Machines[J]. Neural Networks, IEEE Transactions on, 2002, 13(2): 415-425.

(编辑 陈 勇)

Bearing Fault Diagnosis Based on DTCWT and AWTFPSO-optimized SVM

ZHANG Shuqing1HU Yongtao1JIANG Anqi2WU Di1LU Chao1JIANG Wanlu3

1.Institute of Electrical Engineering, Yanshan University, Qinhuangdao,Hebei, 066004 2.School of Information Science and Engineering, Central South University, Changsha, 410006 3.College of Mechanical Engineering,Yanshan University, Qinhuangdao,Hebei, 066004

Based on DTCWT and SVM improved by AWTFPSO, a new method of bearing fault diagnosis was proposed. The mechanical vibration signals were first processed by DTCWT and the energy entropy was extracted as the feature vector. Then, SVM optimized by AWTFPSO was introduced to bearing fault diagnosis. Comparions of different methods show that the proposed method has advantages of high speed and accuracy.

dual-tree complex wavelet transform(DTCWT);support vector machines(SVM);particle swarm optimization(PSO);adaptive weighting and time factor(AWTF);fault diagnosis

2016-04-15

国家自然科学基金资助项目(51475405，61077071)；河北省自然科学基金资助项目(F2016203496，F2015203413)

TN911.6DOI：10.3969/j.issn.1004-132X.2017.03.013

张淑清，女，1966年生。燕山大学电气工程学院教授、博士研究生导师。主要研究方向为弱信号检测、智能信号处理、故障诊断等。发表论文50余篇。E-mail:zhshq-yd@163.com。胡永涛，男，1987年生。燕山大学电气工学院博士研究生。姜安琦，女，1995年生。中南大学信息科学与工程学院本科生。吴 迪，男，1994年生。燕山大学电气工程学院硕士研究生。陆 超，男，1994年生。燕山大学电气工程学院硕士研究生。姜万录，男，1964年生。燕山大学机械工程学院教授、博士研究生导师。