合肥地铁盾构隧道下穿河道施工数值模拟分析

邵 迅, 姚华彦, 张振华, 卢坤林, 胡 众

(1.合肥工业大学 土木工程结构与材料安徽省重点实验室,安徽 合肥 230009; 2.深圳中海建筑有限公司,广东 深圳 518005)

合肥地铁盾构隧道下穿河道施工数值模拟分析

邵 迅1,2, 姚华彦1, 张振华1, 卢坤林1, 胡 众1

(1.合肥工业大学 土木工程结构与材料安徽省重点实验室,安徽 合肥 230009; 2.深圳中海建筑有限公司,广东 深圳 518005)

文章针对合肥地铁1号线盾构下穿南淝河存在的安全隐患,基于流固耦合原理与有限差分方法,采用 FLAC3D对隧道盾构开挖流固耦合效应进行模拟,分析了盾构推进过程中隧道周边土体孔隙水压力规律、竖向应力场、拱顶沉降等。研究表明:盾构开挖导致隧道拱顶及两侧土体孔隙水压力明显降低,地下水在水压力的驱动下向拱顶与两侧流动,这些部位容易出现危险,要防止涌水事故的发生;考虑流固耦合后,围岩竖向应力值变大,最大拉应力与压应力均变大,隧道周边局部围岩出现较大的应力集中现象，对隧洞安全不利,拱顶竖向位移增大,竖向位移在水平方向从隧道中心向两侧不断减小,而土体后期固结沉降占最终沉降的比例达到30%,要加强后期监测,防止沉降过大影响隧道安全。

流固耦合;盾构隧道;数值模拟;应力;沉降

盾构隧道施工中,盾构机掘进会使围岩的应力场进行应力重分布,整个围岩的渗流场相应地发生改变;而围岩渗流场产生的渗流作用力改变也会影响围岩的应力场分布,两者相互影响[1]。岩土体的应力场和渗流场相互耦合作用,将对地层的稳定性造成不良影响,甚至可能危及隧道周围建筑物及地面交通的安全[2]。国内外研究者对隧道工程中的流固耦合问题进行了较为深入的研究。在理论方面,文献[3]考虑地下水渗流场的作用,得到了渗流场作用下围岩与衬砌的应力和位移解析计算式。在数值分析方面,文献[4]研究了盾构隧道施工引起的地面沉降及孔隙水压力分布规律;文献[5-9]采用三维有限元方法建立了渗流场与应力场的耦合计算模型,研究了隧道开挖过程的水-力耦合效应,并将结果应用到工程的设计中。

合肥地铁1号线已开工建设,盾构机即将下穿南淝河,为了保障在下穿南淝河过程中盾构施工的安全,本文以合肥地铁1号线大东门站—芜湖路站区间盾构掘进工程为例,通过FLAC3D模拟隧道盾构开挖过程,研究了盾构掘进过程中模型孔隙水压力变化规律、隧洞的竖向应力、竖向变形等规律,为该段隧道的掘进施工提供技术参考。

1 工程概况

地层分布及隧道相对位置典型剖面图如图1所示。

图1 地层典型剖面图

拟建场地区间上层覆土主要为黏土及粉砂土,岩层主要为中和强风化泥质砂岩,由于区间隧道未穿越土层,对区间隧道影响较大的只有强风化泥质砂岩、中风化泥质砂岩,该岩层属泥质胶结,具有遇水易软化、崩解的特性。当有外部水源或地下水下渗至该岩层,在盾构机掘进扰动的条件下,容易造成风化岩呈泥状破坏。隧洞拱顶距南淝河河床约14 m,上覆土层为粉土和强风化泥质砂岩,这些地层都具有一定的渗透性,在施工扰动情况下,可能在上覆地层中形成裂缝,河水会灌入隧道中,引起严重的安全事故。

2 流固耦合理论及模型的建立

2.1 流固耦合理论基础

FLAC方法求解流固耦合问题时,将岩土体视为多孔介质,流体在孔隙介质中的流动依据Darcy定律,流固耦合过程满足Biot方程。流体在多孔介质中流动时,主要引起孔隙水压力、饱和状态和渗透流量的改变,可通过流体质点平衡方程与Darcy定律来描述流体的流动;本构方程主要表现为孔隙压力、饱和状态、体积应变变化关系,进而实现流体-固体之间的耦合。

对于小变形,流体质点平衡方程为:

(1)

其中,qi,i为渗流速度;qv为被测体积的流体源强度;ζ为单位体积孔隙介质的流体体积变化量。

(2)

其中,M为Biot模量;p为孔隙压力;α为Biot系数;ε为体积应变;T为温度;β为考虑流体和颗粒热膨胀系数。

流体的运动用Darcy定律来描述,对于均质、各向同性固体和流体密度是常数情况,有

(3)

其中,k为介质的渗透系数;ρf为流体的密度;gj(j=1,2,3)为重力加速度的分量。

体积应变的改变引起流体孔隙压力的变化,反过来,孔隙压力的变化也会导致体积应变的发生。孔隙介质本构方程的增量形式为:

(4)

应变率和速度梯度之间的关系为:

(5)

其中,vi,j、vj,i为介质中某点的速度。

在计算中有4种类型的边界条件,分别是:① 给定孔隙水压力;② 给定边界外法线方向流速分量;③ 透水边界;④ 不透水边界。不透水边界为程序中默认,透水边界采用(6)式,即

(6)

其中,qn为边界外法线方向流速分量;h为渗漏系数;p为边界面处的孔隙水压力;pe为渗流出口处的孔隙水压力。

2.2 数值网格模型

本文数值模拟选取里程为K7+268—K7+118路段,拟建线路在里程约为K7+150—K7+210段下穿南淝河。南淝河宽约60 m,水面标高10.2 m。数值计算模型的范围为:顺隧道轴线方向长度取150 m,高程方向取50 m,顺南淝河方向取61 m。

有限元模型单元为六面体等参单元,共划分331 827个单元,包含352 134个节点。模型局部剖面图如图2所示。

图2 模型剖面图

2.3 初始条件与边界条件

(1) 初始条件。初始渗流条件为南淝河水位为10.2 m条件下的初始孔压场,初始应力条件

为南淝河水位为10.2 m条件下自重应力场。

(2) 边界条件。南淝河河水与岸坡表面基础位置为水头边界,盾构掘进掌子面孔压为0,盾构掘进过程中未注浆前的掘进段表面孔压为0;模型底面是基岩,渗透性很小,可认为是不透水边界;模型四周有稳定的地下水位,模型四周边界为水头边界。模型上表面为自由面,模型前、后、左、右侧边界施加水平法向约束,模型底面施加竖向法向约束。

2.4 本构模型和屈服准则

低应力条件下岩土体(含注浆材料)的应力-应变关系基本符合理想弹塑性模型,屈服规律符合Mohr-Coulomb屈服准则。因此,在本次数值模拟计算分析过程中,岩土体的本构模型取弹塑性模型,屈服准则选取Mohr-Coulomb屈服准则。管片、桩等在外荷载作用下,其变形主要处于弹性阶段,其本构模型采用线弹性本构模型。

2.5 计算参数

根据工程地质详勘报告及类似工程类比,数值模拟计算时,地下水体积模量为200 MPa,密度为1 000 kg/m3;管片密度为2 500 kg/m3,弹性模量为30 GPa,泊松比为0.17;注浆体密度为2 400 kg/m3,弹性模量为4 MPa,内摩擦角为25°,黏聚力为15 kPa,泊松比为0.30。其他计算参数取值见表1所列。

表1 部分计算参数

2.6 盾构隧道施工力学过程的数值实现

将盾构推进简化成一个非连续的推进过程,并用改变单元材料类型和参数的方法来反映盾构的推进,模拟计算前,先在模型里预设隧道开挖单元、管片单元及注浆体单元。盾构推进时,假设盾构一步一步跳跃式向前推进,每次向前推进一定的长度,使用model null命令去掉开挖土体,隧道土体开挖后及时改变相应单元的材料模型和参数来模拟管片和注浆体。

3 盾构穿河施工对岩土体的影响分析

结合目前实际的施工进度,盾构下穿南淝河数值模拟时先开挖右线隧道,开挖完毕后再开挖左线隧道;双线隧道共200步开挖完毕,每步1.5 m,1～100步开挖右线隧道,101～200步开挖左线隧道。盾构机在非南淝河段掘进过程中,开挖进度定为每天7步(10.5 m),而盾构机下穿南淝河过程中,开挖进度为每天5步(7.5 m)。

3.1 渗流场分布

盾构开挖导致土体的应力场重分布,土体的渗流场相应地发生改变,以K7+180右洞所在断面为研究对象,选取若干节点作为孔隙水压力监测点,监测点分布如图3所示。随着盾构机在右线隧道掘进过程中孔隙水压力随埋深的分布规律变化情况,如图4所示。K7+180断面右隧洞拱顶距南淝河河床埋深14 m,南淝河河床孔隙水压力固定为0.05 MPa。

图3 孔隙水压力监测点分布

图4 随盾构机推进孔隙水压力随埋深分布曲线

由图4可以发现,开挖前,孔隙水压力基本随埋深的增大线性增大,随着盾构机的推进,开挖面离K7+180断面越来越近,当两者间距10.5 m,埋深8 m以上的孔隙水压力开始有所降低,两者间距减至4.5 m后,埋深5 m以上的孔隙水压力进一步降低,埋深8 m以上的孔隙水压力分布已经和埋深不呈线性关系,埋深12～14 m的孔隙水压力值基本一样。当盾构机刚好穿过K7+180断面右隧洞时,隧洞上方的孔隙水压力已开始进一步降低,孔隙水压力在埋深9 m处最大,埋深9 m以上的孔隙水压力反而降低,拱顶处孔隙水压力由最初的0.19 MPa降至0.02 MPa,这个时间段拱顶孔隙水压力降低最快最大,此时的孔隙水压力比初始值小了近90%。当开挖面离开K7+180断面4.5 m时,隧洞上方孔隙水压力继续降低,孔隙水压力在埋深7.5 m处最大;埋深增加,孔隙水压力反而降低。开挖面离开15.0 m后,各点孔隙水压力继续小幅降低,待右线隧道开挖完毕(开挖面离开断面60.0 m),孔隙水压力又降低,但是降幅很小,说明后期孔隙水压力的变化不大。右线隧道开挖完毕后,随着埋深的增大,孔隙水压力降低,孔隙水压力分布规律与开挖前完全不同,这是因为隧洞开挖改变了原始渗流场,隧洞周边的孔隙水压力降低。

K7+145断面在隧道开挖贯通后的孔隙水压力等值线云图如图5所示(单位为Pa)。由于开挖扰动,岩土体孔隙水压力重新分布,隧道周边孔隙水压力开始下降,计算软件程序中设定开挖部分孔隙水压力为0,远场地下水在孔隙水压力的驱动下向开挖临空面流动,最终在隧道表面附近呈现类似降水漏斗型的稳态分布,这与文献[10]的结论一致。

K7+145断面地下水渗流场流动矢量分布规律如图6所示,可见隧道开挖完毕后,地下水快速向隧道内部渗透,拱顶与两侧流动矢量分布更为密集,说明渗透部位主要集中在拱顶与两侧,这些部位容易出现危险,若施工不当,很可能引发涌水,在开挖过程中要重点关注。

图5 孔隙水压力分布

3.2 应力场分布

盾构隧道施工中,盾构机掘进会使围岩的应力场进行应力重分布,整个围岩的渗流场相应地发生改变;而围岩渗流场产生的渗流作用力改变也会影响围岩的应力场分布。因此,是否考虑流固耦合直接影响围岩的应力场分布。考虑流固耦合和不考虑流固耦合2种情况下隧道开挖后围岩竖直方向的应力如图7所示(单位为Pa)。

从图7可以看出,在2种情况下,隧道的开挖都导致了岩体内部应力场重新分布,隧道周边局部围岩出现较大的应力集中现象,隧洞两侧局部出现较高压应力,而隧洞拱顶出现较小的拉应力,拱底处竖向总应力值较小。

与不考虑渗流时的围岩应力场相比,考虑渗流时围岩应力分布相似,但是竖向应力值变大,最大拉应力及压应力也变大。K7+185断面,最大拉应力由0.016 MPa升至0.039 MPa,最大压应力由0.97 MPa升至1.17 MPa;K7+155断面,最大拉应力由0.016 MPa升至0.092 MPa,最大压应力由1.04 MPa升至1.26 MPa。出现这个现象主要是由于隧道开挖后渗流场发生变化,进而导致应力场变化。

3.3 隧道拱顶沉降

盾构开挖会使原来的土体平衡状态受到破坏,围岩就会产生移动。隧洞拱顶竖向位移直接关系到隧道的安全,在盾构施工中,要及时监控拱顶位置土体的竖向位移,采取措施加以控制。为了研究拱顶竖向位移在盾构开挖过程中的变化规律,在K7+185断面右洞(对应开挖第59步)拱顶和拱顶两侧共设定7个测点,每个测点高程一样,水平间距为3 m,其中1个点位于拱顶处,其余6个点分别位于拱顶两侧。随盾构机推进,测点位移变化曲线如图8所示。

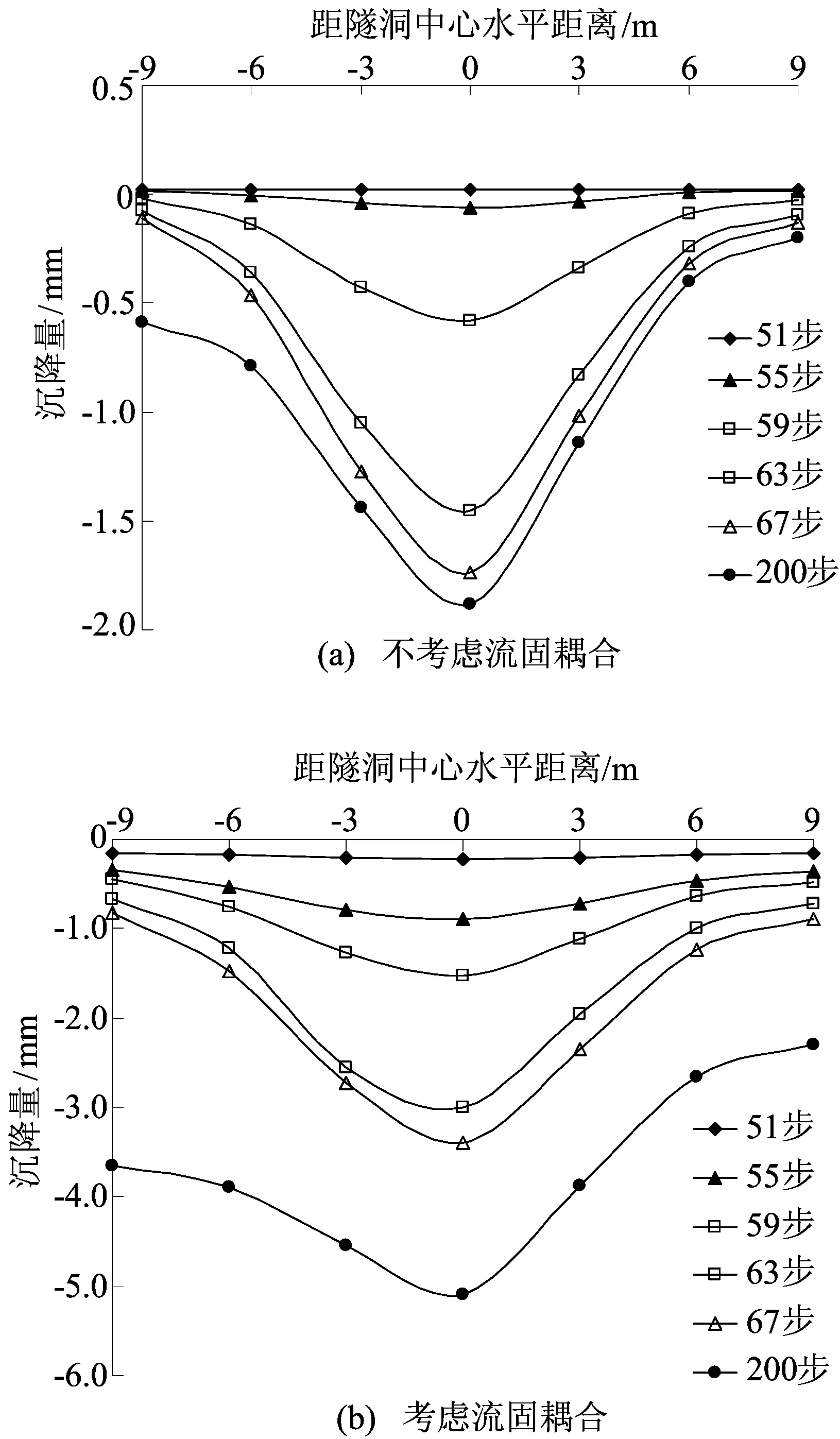
图8 随盾构机推进隧洞周边测点位移曲线

由图8可知,考虑流固耦合后,竖向位移明显增大;竖向位移在水平方向从隧道中心向两侧不断减小,类似于Peck曲线[11]。随着盾构机的推进,隧道施工对拱顶周边沉降影响范围扩大;推至51步时,各测点位移基本一样,不考虑耦合时各测点有少许隆起变形,而考虑耦合时各测点已有沉降变形;推至55步后,各测点沉降量不断增加,沉降增量在盾构机推近K7+185断面至推过K7+185断面这段过程中呈现先增加后减少的特点,但是增量最大处不是出现在盾构机刚推过断面处,而是推过一段距离之后。其原因是盾构机刚推至59步时,盾构机刀盘可为周围土体起到支护作用,一定程度上抑制了沉降增量;而离开59步后,盾构机不再发挥支护作用,沉降增量增大,而衬砌和注浆刚刚完成,起到支护作用还需一段时间,经过一段时间之后,衬砌和砂浆对土体的支护作用显现,沉降增量又变小。当开挖面在断面前后12 m即2D(隧道直径)范围时,各测点沉降变化显著。

开挖完毕后的最终沉降量,不考虑流固耦合时,与开挖至67步的沉降量相差不大,而考虑流固耦合后,土体后期固结沉降占最终沉降量的比例较大,经计算67步以后所有测点的沉降量增量占最终沉降量的比例达到30%以上,说明流固耦合作用下隧道周边土体固结对隧道变形也有影响[9,12]。因此,在施工监测中要注意加强后期沉降测量。

4 结 论

本文以合肥地铁1号线盾构施工下穿南淝河工程为例,利用 FLAC3D数值软件进行了隧道盾构开挖模拟,得到了如下结论:

(1) 隧洞开挖导致隧洞四周产生水压应力差,进而造成了渗流场的改变,最终形成一个类似降水漏斗的形状,开挖前、后孔隙水压力随埋深的关系发生变化。拱顶与两侧流动矢量分布更为密集,这些部位容易出现危险,要防止涌水事故的发生。

(2) 盾构开挖后,隧道周边局部围岩出现较大的应力集中现象,隧洞两侧局部出现较高压应力,而隧洞拱顶出现较小的拉应力,拱底处竖向总应力值较小。与不考虑渗流时的围岩应力场相比,考虑渗流后竖向应力值变大,最大拉应力与压应力也变大,水的渗流对隧道整体稳定性不利。考虑流固耦合之后,竖向位移明显增大。竖向位移在水平方向从隧道中心向两侧不断减小,当开挖面在断面前后12 m即2D(隧道直径)范围时,拱顶附近土体沉降变化显著。土体后期固结沉降占最终沉降量的比例较大。

(3) 盾构开挖过程中应采取保压、稳压匀速掘进,严格控制出土量和出土速度并做好相应记录,减少盾构施工对地层的扰动,避免因出土过快、仓压过低在地层中形成较大的水流通道;要及时注浆,控制好拱顶沉降,同时加强监控测量。

[1] 李皓晖,左昌群,唐霞,等.变质软岩隧道施工中地下水渗漏处治措施[J].铁道建筑,2015(3):76-79.

[2] 吉小明,王宇会,阳志元.隧道开挖问题中的流固耦合模型及数值模拟[J].岩土力学,2007,28(增刊):379-384.

[3] 蔡晓鸿.设集中排水的水工压力隧洞含水围岩弹塑性应力分析[J].岩土工程学报,1991,13(6):52-63.

[4] YI X,ROWE R K,LEE K M.Observed and calculated pore pressures and deformations induced by an earth balance shield[J].Canadian Geotechnical Journal,1993,32(30):476-490.

[5] 张黎明,李鹏,孙林娜,等.考虑地下水渗流影响的衬砌隧洞弹塑性分析[J].长江科学院院报,2008,25(5):84-87,93.

[6] 陈卫忠,邵建富,DUVEAU G,等.粘土岩饱和-非饱和渗流应力耦合模型及数值模拟研究[J].岩石力学与工程学报,2005,24(17):3011-3016.

[7] 靳晓光,李晓红,张燕琼.越江隧道施工过程的渗流-应力耦合分析[J].水文地质工程地质,2010,37(1):62-67.

[8] 纪佑军,刘建军,程林松.考虑流-固耦合的隧道开挖数值模拟[J].岩土力学,2011,32(4):1229-1233.

[9] 张玉军,张维庆.考虑裂隙的几何-力学特性的双重孔隙介质水-应力耦合模型及其有限元分析[J].水利学报,2009,40(12):1452-1459.

[10] 陈发本,黄德镛,杨卓.考虑流固耦合的富水隧道开挖对比分析[J].交通科学与工程,2013,29(2):56-62.

[11] PECK R B.Deep excavations and tunneling in soft ground[C]//Proceedings of the 7th International Conference on Soil Mechanics and Foundation Engineering.Mexico City:[s. n.],1969:225-290.

[12] 袁先机.盾构隧道穿越土坝的地层沉降控制[J].合肥工业大学学报(自然科学版),2003,26(5):1105-1109.

(责任编辑 张淑艳)

Numerical simulation analysis of Hefei metro shield tunnel crossing river

SHAO Xun1,2, YAO Huayan1, ZHANG Zhenhua1, LU Kunlin1， HU Zhong1

(1.Anhui Key Laboratory of Structure and Materials in Civil Engineering, Hefei University of Technology, Hefei 230009, China; 2.China Overseas(Shenzhen) Construction Co., Ltd., Shenzhen 518005, China)

In order to resolve the potential danger of shield tunnel crossing Nanfeihe River on Hefei Metro Line 1, the fluid-structure interaction effect was simulated based on fluid-structure interaction principle and finite difference method by FLAC3D, and the pore water pressure around the tunnel, vertical stress field and crown sedimentation induced by shield structure excavation were analyzed. It was indicated that the pore water pressure around the arch apex and surrounding soil was seen great reduction, so the underground water driven by the pressure difference tended to flow into these areas, which might present danger such as water burst. Considering the fluid-structure interaction principle, the vertical stress value of surrounding rock would grow; the maximum tension stress and pressure stress would also grow. A massive stress concentration occurred in surrounding rock of tunnel is dangerous. The vertical displacement of arch apex grew and this value constantly decreased from center to the sides horizontally. The proportion of later consolidation settlement in the ultimate settlement could reach 30%. So the further monitoring was needed to keep the tunnel from risks by massive settlement.

fluid-structure interaction; shield tunnel; numerical simulation; stress; sedimentation

2015-11-03；

2015-11-17

国家自然科学基金资助项目(51409076)；水利部公益性行业科研专项经费资助项目(201401063 )和合肥市轨道交通质量监督站专项经费资助项目(2014CGFZ0200)

邵 迅(1990-),男,安徽庐江人,合肥工业大学硕士生; 张振华(1977-),男,福建政和人,博士,合肥工业大学教授,硕士生导师.

10.3969/j.issn.1003-5060.2017.01.018

TU921

A

1003-5060(2017)01-0095-06