CFRP约束有预载矩形SRC短柱轴压性能有限元分析

高 鹏, 宗 文, 李仲元, 殷 强, 洪 丽

(合肥工业大学 土木与水利工程学院,安徽 合肥 230009)

CFRP约束有预载矩形SRC短柱轴压性能有限元分析

高 鹏, 宗 文, 李仲元, 殷 强, 洪 丽

(合肥工业大学 土木与水利工程学院,安徽 合肥 230009)

为了研究预载水平对碳纤维增强聚合物(carbon fiber reinforced polymer,CFRP,又称为“碳纤维布”)约束型钢混凝土(steel reinforced concrete,SRC)矩形短柱轴压性能的影响,文章采用有限元软件对已有试验试件进行了数值模拟,结果表明采用混凝土损伤塑性模型可较好地模拟预载后加固型钢混凝土柱在有材料损伤后的力学性能。通过数值分析发现,碳纤维布对型钢混凝土矩形短柱的约束作用主要集中在水平截面的柱角部和靠近型钢部位;预载水平提高后,峰值荷载下试件中混凝土的竖向应力降低,且远离型钢部位的柱角部混凝土应力变化最明显,同时预载水平对碳纤维布工作应变有影响；建立了预载水平与碳纤维布有效拉应变的关系式。

预载水平;碳纤维布约束;型钢混凝土矩形短柱;轴压性能;竖向应力;有效拉应变

在混凝土加固中碳纤维增强聚合物(carbon fiber reinforced polymer,CFRP,又称为“碳纤维布”)具有力学性能优良、施工方便、加固效果明显等优点,采用纤维增强聚合物(fiber reinforced polymer,FRP)加固混凝土构件能显著提高构件的强度和变形能力,同时克服了传统加固方法的缺陷,其工程应用是近年来研究的热点[1-2]。但在FRP加固设计中,大多数的混凝土柱都处于一定的负载状态,构件内部具有初始应力,此时外包的FRP就必然存在一定的应变滞后。大量研究表明,初始应力导致的FRP应变滞后对混凝土柱加固效果有影响[3-4]。

为全面探究FRP加固混凝土构件的受力机理,消除试验偶然因素,需要借助有限元软件进行模拟与分析。文献[5]通过有限元分析,得出约束混凝土方柱截面上混凝土应力分布和纤维在不同方向上的应变变化;文献[6]分析横向箍筋的约束机制,得出离箍筋不同截面处的应力分布;文献[7]进一步分析了圆角半径对混凝土截面最大主应力与最小主应力比值分布的影响,得出圆角区域和核心区域的应力比值较大;文献[8]采用单元生死法,很好地模拟了CFRP加固有负载的混凝土构件。但目前对于模拟加固有卸载过程的混凝土构件,如何实现材料损伤以及FRP的应变滞后效应仍是建模分析的关键。

本文在试验的基础上[9],使用ABAQUS软件建立有限元模型,进一步探究CFRP约束预载型钢混凝土柱的受力性能和受力机理。

1 试验概况

试验设置7组具有不同预载水平的CFRP约束型钢混凝土矩形短柱试件和2组无预载对比试件,分别进行轴压性能测试,见表1所列。

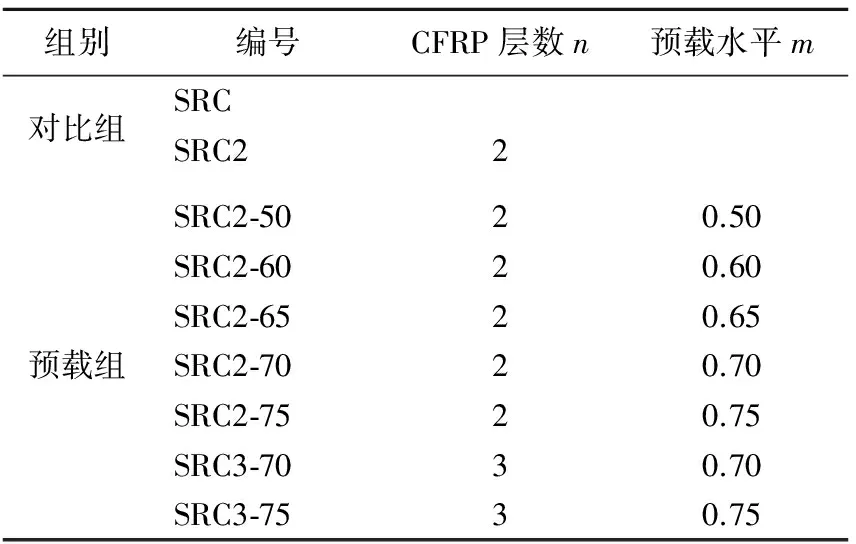
表1 试件参数

注:预载水平m表示预加荷载与未约束型钢混凝土矩形 短柱SRC峰值荷载的比值；试件编号如为SRC2-50, 数字2表示包裹2层,50表示预载水平为0.50。

图1 试件设计图

根据试验标准测得所采用的混凝土和钢筋材料强度,其中等级为C30的混凝土立方体抗压强度实测值为32.1 MPa,弹性模量为26.1 GPa,型钢和纵筋的抗拉屈服强度实测值分别为227.0、465.0 MPa,弹性模量分别为170.0、200.0 GPa。根据厂家提供的数据,碳纤维布的抗拉强度为3 506.0 MPa,弹性模量为242.0 GPa,单层厚度为0.111 mm。

预载组的试件会在设计的预载水平下进行加卸载5次,待残余应变基本达到稳定后再包裹CFRP布进行正式加载试验。试验中用力传感器测量试件所受压力,在柱高中部处的混凝土表面布置应变片量测竖向受压应变,在碳纤维布环向设置受拉应变片。各约束加固后构件均呈现弱约束破坏模式。正式加载初期,试件表面逐渐有裂缝开展,当荷载接近峰值时,纤维开始有撕裂声,型钢和纵筋先后屈服;荷载在达到峰值后开始缓慢下降,纤维撕裂声逐渐增多,最后因核心区混凝土被压碎,CFRP布发生突然断裂而破坏。

2 数值模型

2.1 混凝土损伤塑性模型

混凝土材料采用ABAQUS软件中损伤塑性模型(concrete damaged plasticity,CDP)[10],该模型将损伤指标引入混凝土模型,通过对混凝土的弹性刚度矩阵加以折减,模拟混凝土刚度随损伤增加而降低的特点[11]。在弹性阶段,该模型采用线弹性模型对材料的力学性能进行描述,进入损伤后,弹性模量可表示为:

(1)

其中,E0为无损伤弹性模量;d为损伤因子,用于描述卸载时材料刚度退化等现象,它是应力状态和单轴拉压损伤变量的函数。确定损伤因子的方法已有大量研究[12-14]。本文采用文献[15]中的混凝土本构关系,引入损伤变量,并根据能量等效原理计算出所需参数[16]。

2.2 材料参数

在软件中建立三维实体模型,其中混凝土采用实体单元C3D8R,选用文献[15]中的本构关系,如图2所示,轴心抗压强度和初始弹性模量取试验测试值,泊松比为0.2;型钢采用实体单元C3D8R,箍筋和纵筋采用桁架单元T3D2,钢材的应力-应变曲线均采用理想弹塑性,型钢和纵筋的抗拉屈服强度和弹性模量取试验测试值;碳纤维布采用膜单元M3D4R,弹性模量根据厂家提供的数据,分析时只考虑沿纤维方向的弹性拉应力。

在软件中对试件的预载、加固和正式加载受力全过程进行模拟。模型柱的底部设为固定端,上部设为允许轴向移动的加载端,预载阶段在顶部施加力荷载,正式加载阶段施加位移荷载。采用单元生死法来实现不同阶段碳纤维布的约束情况,在预载阶段将碳纤维布单元杀死,使其不承受外力,在随后的正式加载阶段将碳纤维单元激活并与其他单元共同受力,使内部混凝土处于受约束状态。

通过试验可知,型钢和混凝土之间以及CFRP和混凝土之间具有较好的黏结,因此采用分离式的钢筋混凝土有限元模型,模型中不考虑材料之间的黏结滑移,均采用绑定连接,使对应单元的节点位移协调。模拟计算中若试件中的CFRP应变达到试验时的断裂应变,则认为加载到极限破坏状态,终止计算;在参数分析计算中,由试验可知在弱约束作用下,试件中CFRP断裂一般发生在峰值荷载后下降到0.85倍承载力时,因此在此时终止计算。

图2 混凝土本构曲线

3 模型验证与分析

为验证试件模型的准确性,将正式加载过程中荷载与试件中部混凝土竖向应变的试验结果与数值计算曲线进行对比,如图3所示。在加载前期,荷载值较小时,两者变化趋势吻合较好;当轴向荷载较大时,混凝土裂缝开展迅速,试验中应变片数据波动较大,峰值后期有应变片脱落现象。试件峰值荷载的计算值与试验值的比较见表2所列,误差介于0.4%～18.6%之间。

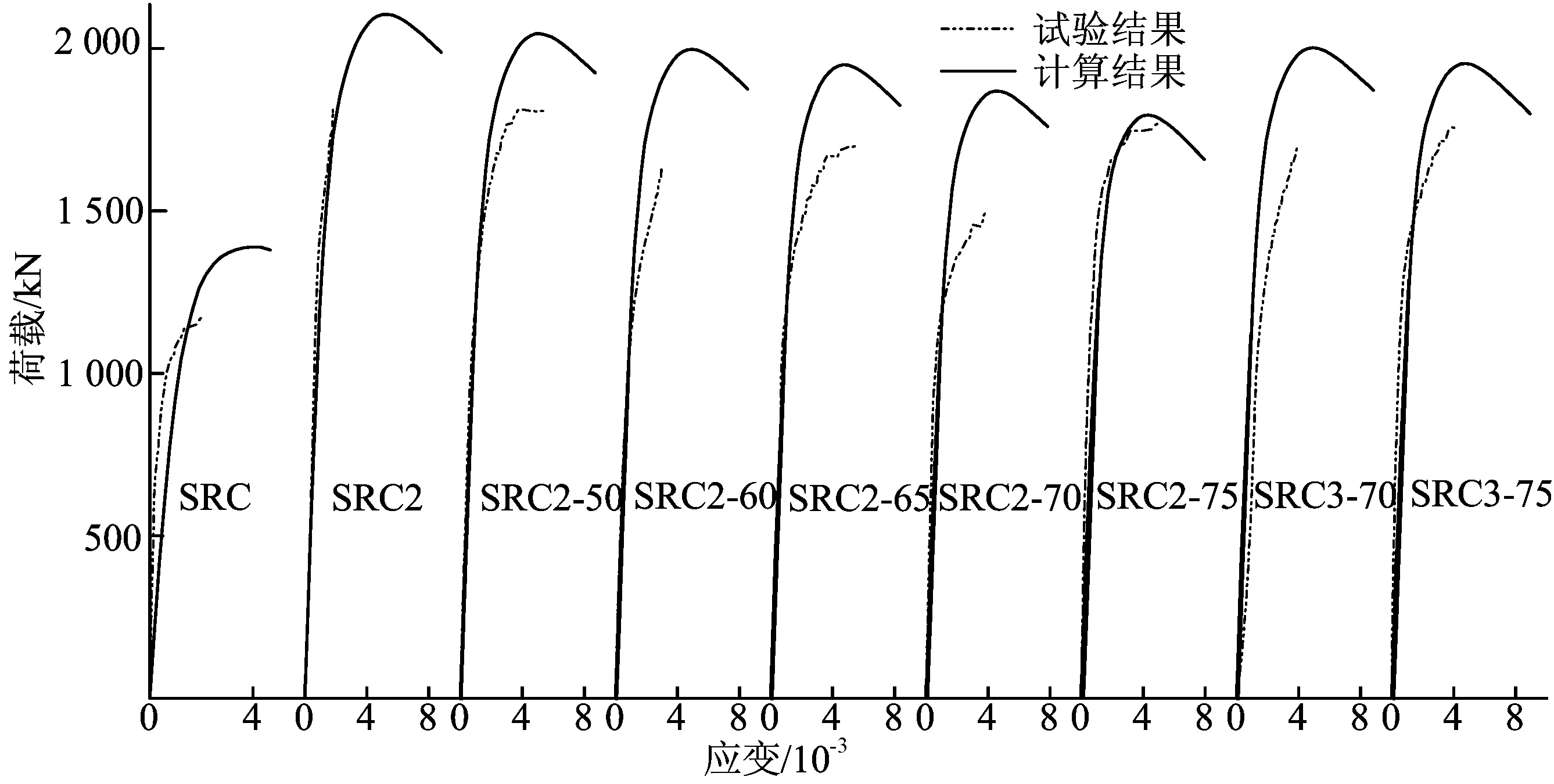
图3 轴向荷载-应变曲线对比

kN

SRC2-50柱破坏形态对比如图4所示,极限状态时试件破坏形态的数值结果与试验结果基本一致。

破坏时柱核心混凝土被压碎,体积向外围扩展,柱中部侧向水平变形大于柱两端。从图4b中还可见柱高中部CFRP条带应变值大于柱端部条带的应变值;在每个条带内,横截面上边长中部的CFRP应变值大于柱角部。

图4 SRC2-50柱破坏形态对比

4 受力分析

4.1 混凝土截面应力

峰值荷载时,为反映试件在不同预载水平下混凝土截面应力大小及分布的变化,选取4个典型构件,其中间横截面混凝土竖向应力分布如图5所示,其中正值表示受压,由于柱截面的对称性,只取1/4部分。

由图5可发现,碳纤维布在型钢混凝土矩形柱角部位置约束能力最强,沿对角线方向逐渐减小,随后在型钢附近的范围内又逐渐增大;尤其在型钢两翼缘和腹板之间存在较强约束区。这说明型钢的腹板和翼缘在核心区有效抑制了混凝土的膨胀,形成了对混凝土较好的约束效果。而在靠近柱边长中部区域,由于碳纤维布变形伸长量较大,混凝土有较好的侧向膨胀,且竖向应力较低;混凝土应力变化趋势从内部型钢核心位置向柱边中点方向逐渐减弱。

比较图5a～图5c可知,随着预载水平的提高,峰值荷载时柱中截面混凝土应力不断降低。当预载水平从0增加到0.50时,角部混凝土强度从36MPa降低到33MPa,降低了8.3%;核心区混凝土强度从24MPa降低到23MPa,降低了4.2%。当预载水平从0.50增大到0.75时,角部混凝土强度从33MPa降低到25MPa,降低了24.2%;核心区混凝土强度从23MPa降低到20MPa,降低了13.0%,可见施加预载对混凝土竖向应力造成了显著影响,削弱了约束效果;但型钢两翼缘之间核心约束区应力的降低幅度低于柱角部应力,预载对远离型钢部位的角部混凝土应力影响更明显。随着预载水平提高,柱角部强约束区的面积不断减小,而柱各部分混凝土应力梯度值也趋于均匀,这说明约束加固措施可有效提高预载后有损伤型钢混凝土柱材料性能的发挥,挖掘了构件潜力。

比较图5c和图5d可知,随着碳纤维布层数的增加,CFRP对于预载柱的约束效果有所增加,主要集中在角部。角部最大竖向应力从25MPa增加到29MPa,提高了16%,但由于受强约束的角部区域面积较小,增加碳纤维布层数对预载柱的纵向承载力提高有限。

由表2可看出,试验中预载水平为0.75时,构件在从2层碳纤维布增加到3层时,其承载力从1 787kN增加到1 808kN,提高了1.2%[9]。

图5 混凝土横截面应力分布图

4.2CFRP约束应力

为反映试件关键部位在加载过程中约束应力的发展过程,选取柱中截面角部中点(如图5a中的A点)和边长中点(如图5a中的B点)处2个关键点,建立CFRP对混凝土的侧向约束应力fl与轴向峰值荷载F的关系曲线,如图6所示,分别取0.3F、0.5F、0.8F、F时对应的约束应力值。在峰值荷载前,2个点的约束应力随轴向荷载的增大而不断增大,但柱高中部边长中点B的约束应力远小于角部中点A的约束应力,说明CFRP对矩形截面型钢混凝土柱的约束作用主要集中在水平截面的柱角部,对柱中部混凝土的约束作用较小。同时,当轴向荷载小于0.5F时,CFRP对混凝土的约束作用较小,之后开始缓慢增加,当荷载达到0.8F时,约束应力急剧增加,说明CFRP对混凝土约束作用主要发生在混凝土进入不稳定发展阶段后。

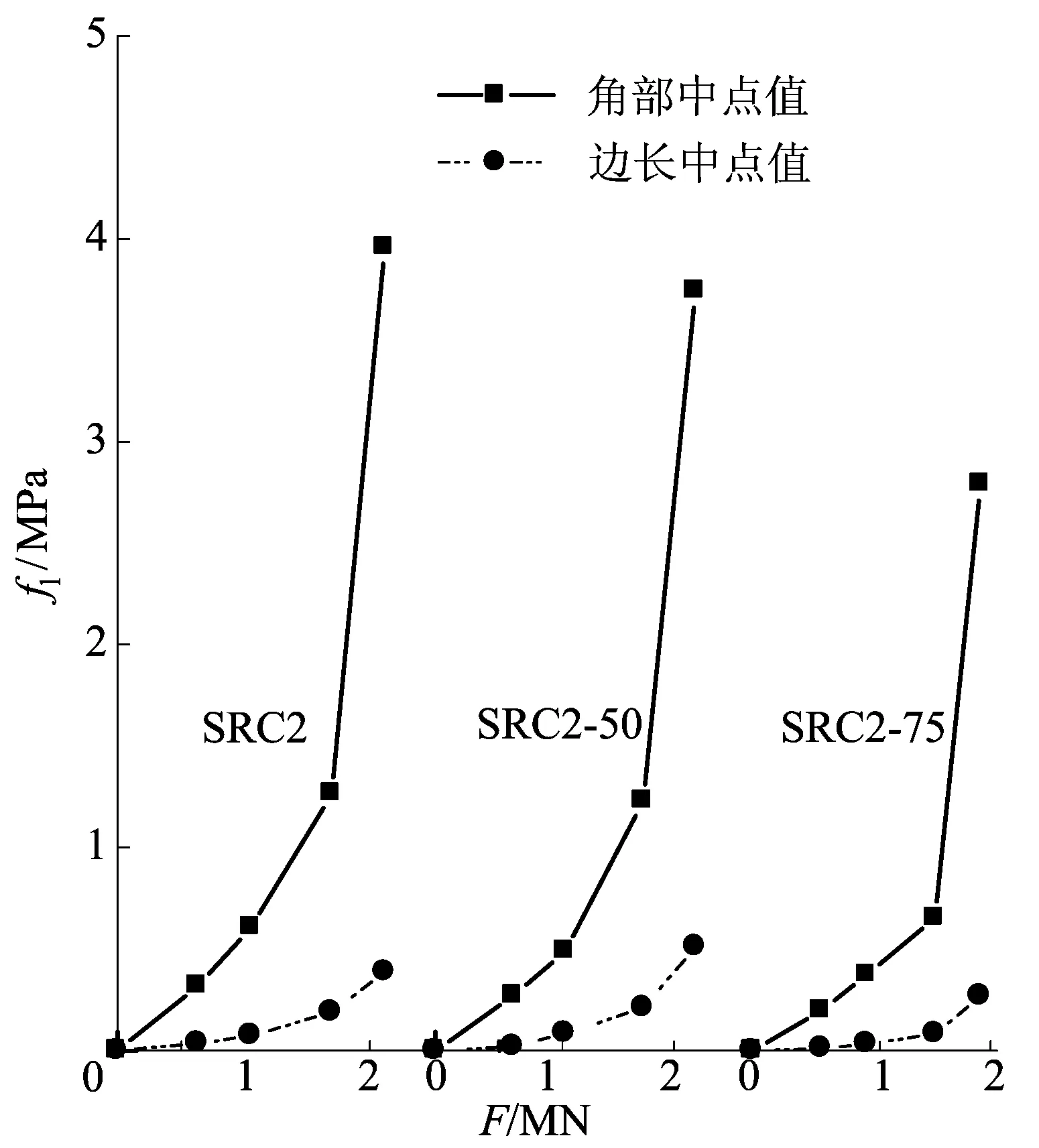
图6 约束应力与轴向荷载关系曲线

4.3 碳纤维布应变

(1) 应变环向分布。柱在峰值荷载时,碳纤维布拉应变沿1/2柱高处截面的环向应变分布如图7所示(其中纵轴表示碳纤维布在峰值荷载时的拉应变εfpe与碳纤维布的理论极限拉应变εfu的比值,横轴表示应变片在柱长边的相对位置,其中0表示柱长边中点,1表示柱角点)。

由图7可见,柱中部的CFRP环向相对应变约为柱角部相对应变的2倍,其原因是柱在峰值荷载时柱中部的混凝土侧向变形比角部混凝土的侧向变形要大。另外,碳纤维布拉应变随着预载水平的增大而减小,当预载水平从0增加到0.50时,柱中部的CFRP相对应变从0.289降低到0.279,降低了3.6%;当预载水平从0.50增加到0.75时,柱中部的CFRP相对应变从0.279降低到0.238,降低了14.7%,可以看出预载水平越大,CFRP应变的降低幅度越大,这是因为型钢柱在经过预载损伤后,其混凝土已经形成一定的侧向变形,且随着预载水平的增大柱的侧向变形变大;实施CFRP约束加固后是在已有受损柱上进行的,此时CFRP的环向拉应变滞后于表面混凝土应变,从而降低了柱的加固效果。

图7 峰值荷载时碳纤维布环向应变分布

(2) 预载水平的影响。预载使混凝土开裂后,导致裂缝处的碳纤维布应力突变;而碳纤维布的环向拉应变滞后于受损混凝土的表面应变,也影响其应变发挥。因此,本文提出预载型钢混凝土矩形加固柱碳纤维布的环向拉应变折减系数为km,其碳纤维布的有效环向拉应变为εef=km×(σf/Ef)。其中,σf为碳纤维布拉应力,Ef为碳纤维布弹性模量。碳纤维布环向有效拉应变的折减系数和预载水平的关系如图8所示,经回归得到km的关系式为:

km=0.587-0.298m3

(2)

图8 碳纤维布环向有效拉应变与预载水平的关系

为更好地反映不同预载水平的影响,在SRC2-50柱模型的基础上,进一步分析了预载水平为0.20、0.30、0.40、0.80的型钢混凝土试件,在弱约束破坏模式下,在峰值荷载后下降到0.85倍承载力时终止计算,得到此时碳纤维布断裂应变的数据。同时由文献[17]得到预载水平为0.40、0.80下约束钢筋混凝土方柱的碳纤维布有效环向拉应变。

5 结 论

本文采用有限元软件对碳纤维布约束型钢混凝土矩形短柱的轴压破坏过程进行了数值模拟,根据结果对其受力机理进行分析,得出如下结论:

(1) 数值计算中采用文献[15]提供的混凝土本构关系,并依据能量等价原理计算损伤因子,将数值与试验结果对比分析,验证了使用CDP混凝土材料模型能较好地模拟预载后约束加固型钢混凝土柱在混凝土有损伤发展时的力学性能。

(2) 碳纤维布对矩形截面型钢混凝土柱的约束作用主要集中在水平截面的柱角部和靠近型钢的核心位置,当加载到80%的峰值荷载时才有明显的约束作用;随着预载水平增大，峰值荷载时混凝土竖向应力不断降低,且远离型钢部位的柱角部混凝土应力的变化最明显。

(3) 峰值荷载时,碳纤维布在柱中部的环向相对应变约为柱角部相对应变的2倍,且各位置上碳纤维布应变值随预载水平的增大而降低。

[1] 国家工业建筑诊断与改造工程技术研究中心.碳纤维片材加固混凝土结构技术规程:CECS 146:2003 [S].北京:中国计划出版社,2003:15-38.

[2] 王慧,吴志平,王萱.外贴碳纤维增强材料加固混凝土梁的抗弯设计方法[J].合肥工业大学学报(自然科学版),2003,26(3):416-421.

[3] 曹双寅,潘毅,敬登虎,等.负载下碳纤维布约束混凝土圆柱轴压应力-应变关系试验研究[J].东南大学学报(自然科学版),2008,38(5):788-793.

[4] 敬登虎.GFRP 加固RC 柱应变滞后分析[J].特种结构,2003,20(3):74-76.

[5] 陆新征,冯鹏,叶列平.FRP布约束混凝土柱轴心受压性能的有限元分析[J].土木工程学报,2003,36(2):46-51.

[6] TENG J G，XIAO Q G，YU T，et al.Three-dimensional finite element analysis of reinforced concrete columns with FRP and/or steel confinement[J].Engineering Structures，2015，97:15-28.

[7] NISTICO N.R.C.square sections confined by FRP:a numerical procedure for predicting stress-strain relationships [J].Composites Part B:Engineering，2014，59:238-247.

[8] 熊学玉,徐海峰,李亚明.负载下CFRP布约束钢筋混凝土矩形柱轴心受压性能分析[J].土木工程学报,2010,43(6):26-33.

[9] 王健.碳纤维布约束有预载型钢混凝土矩形短柱轴压性能研究[D].合肥:合肥工业大学,2015.

[10] ABAQUS Inc.Abaqus theory manual [Z].Lexington，Kentucky,US:ABAQUS Inc,2007.

[11] 江见鲸,陆新征,叶列平.混凝土结构有限元分析[M].北京:清华大学出版社,2005:225-235.

[12] 郭明.混凝土塑性损伤模型损伤因子研究及其应用[J].土木工程与管理学报,2011，28(3):128-132.

[13] 薛志成,马强,杨璐,等.混凝土受压损伤本构模型及其数值验证[J].混凝土,2012(5):41-43.

[14] 张战廷,刘宇锋.ABAQUS中的混凝土塑性损伤模型[J].建筑结构,2011,41(增刊2):229-231.

[15] 中华人民共和国住房和城乡建设部.混凝土结构设计规范:GB 50010—2010 [S].北京:中国建筑工业出版社,2010:202-235.

[16] 李兆霞.损伤力学及其应用[M].北京:科学出版社,2002:46-51.

[17] 王震宇,王代玉,吕大刚,等.CFRP 中等约束钢筋混凝土方柱单轴受压应力-应变模型[J].建筑结构学报,2011,32(4):101-109.

(责任编辑 张淑艳)

Finite element analysis of axial compressive behavior of CFRP-confined preloaded steel reinforced concrete rectangular short column

GAO Peng， ZONG Wen， LI Zhongyuan， YIN Qiang， HONG Li

(School of Civil and Hydraulic Engineering， Hefei University of Technology， Hefei 230009， China)

To analyze the effect of preload level on the behavior of carbon fiber reinforced polymer(CFRP)-confined steel reinforced concrete(SRC) rectangular short columns under concentric compression， the compressive behavior of the specimens designed in the experiments was simulated by the finite element method. It was found that the concrete damaged plasticity model could predict the mechanical properties of the rehabilitated preloaded SRC columns at a reasonable degree of accuracy. The effects of confinement offered by CFRP mainly focused on the corner zones of columns and the zone near steel. The vertical stress of concrete in columns decreased with the increase of the preload level under the peak load，in which the corner zones decreased most obviously. Meanwhile， the preload level also influenced the circumferential strain of CFRP. Based on the previous researches， the relationship between the preload level and the effective circumferential strain of CFRP was proposed.

preload level; carbon fiber reinforced polymer(CFRP) confinement; steel reinforced concrete(SRC) rectangular short column; axial compressive behavior; vertical stress; effective circumferential strain

2015-09-21；

2015-12-07

国家自然科学基金资助项目(51208166);安徽省高等学校省级优秀青年人才基金资助项目(2011SQRL011)

高 鹏(1978-),男,安徽合肥人,博士,合肥工业大学副教授,硕士生导师.

10.3969/j.issn.1003-5060.2017.01.016

TU375.3

A

1003-5060(2017)01-0083-06