基于支持向量分位数回归的货币需求条件密度预测研究

(1.合肥工业大学 管理学院,安徽 合肥 230009; 2.合肥工业大学 过程优化与智能决策教育部重点实验室,安徽 合肥 230009)

基于支持向量分位数回归的货币需求条件密度预测研究

许启发1,2, 俞奕涵1, 蒋翠侠1

(1.合肥工业大学 管理学院,安徽 合肥 230009; 2.合肥工业大学 过程优化与智能决策教育部重点实验室,安徽 合肥 230009)

考虑到货币需求与其影响因素之间复杂的关系,基于支持向量分位数回归(support vector quantile regression,SVQR)模型,文章研究了货币需求及其影响因素之间的非线性依赖关系,给出了货币需求条件密度预测方法,并将其与传统的线性分位数回归模型进行了比较。选取中国2004年1月至2014年12月期间工业增加值、消费物价指数(consumer price index,CPI)、利率与M1的月度数据进行实证研究,结果表明SVQR模型不仅能够很好地拟合货币需求,而且能够给出准确的概率密度预测结果。

货币需求;分位数回归;支持向量分位数回归(SVQR);条件密度预测;广义近似交叉验证(GACV)准则

近年来,关于货币需求分析的经济计量模型与方法的研究成果层出不穷。文献[1]指出货币需求是内生的,不能直接观测得到,不过可以通过货币供应与货币需求一致性,将可观测的货币供应量M1、M2作为货币需求量的代表;文献[2]研究发现M1与实际GDP、一年期定期存款利率存在协整关系;文献[3]引入了货币化程度变量,实证研究分析结果表明,M1、M2分别和收入、利率、货币化程度变量、价格预期之间都存在线性关系;文献[4]从经典的货币需求理论出发,采用协整理论和误差修正模型研究货币需求与国民收入、利率和通货膨胀之间的关系;文献[5]从我国经济转型角度,采用动态建模方法对中国经济转型过程中的货币需求函数进行了再估计,通过引入市场化进程相对指数作为衡量经济转型的制度变量考察货币需求、经济增长、通货膨胀、利率和经济转型之间的相互关系;文献[6]利用均值局部调整模型对货币需求问题进行了讨论;文献[7]把分位数回归应用于货币市场,并基于分位数回归变参数检验,讨论了前瞻性利率规则在中国的适用性;文献[8]提出了分位数局部调整模型,并将此模型应用于中国货币需求分析,结果发现在货币需求的不同阶段,不仅调整速度不同,而且调整方式也呈现出非对称性。

由以上研究可以看出,货币需求分析模型经历了从均值回归到分位数回归的转变过程。但是,这些研究工作主要使用了线性模型设置,难以有效揭示货币需求及其影响因素之间复杂的非线性关系。为此,本文采用支持向量分位数回归(support vector quantile regression，SVQR)模型,对货币需求问题开展定量研究。一方面,通过支持向量机的非线性模拟能力,揭示货币需求系统中的非线性依赖关系;另一方面,通过分位数回归,更加细致地揭示货币需求在不同分位点处对影响因素的依赖关系,进而完整地描述整个货币需求分布特征的动态变动规律。

1 模型与方法

1.1 模型表示

基于统计学习理论建立起来的支持向量机,在模式识别等领域发挥重要作用。近年来,支持向量机常被应用于解决回归问题,成为支持向量回归,其数学模型为:

(1)

其中,φ(·)为非线性映射;ω为参数向量;b为阈值。对于模型参数的估计,可以采用(2)式进行优化,即

(2)

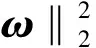
(3)

其中,ε为管道尺寸,若取值越大,则训练样本中支持向量样本的个数越少;反之,支持向量样本的个数越多。

1.2 模型求解

(4)

(5)

文献[10]最早提出SVQR模型;文献[11-12]利用半参数方法,得到了一个更为简单的SVQR模型,在含有软化ε带支持向量回归(support vector regression,SVR)模型中,用分位数回归替代惩罚函数部分,得到的SVQR模型可以表示如下:

(6)

(7)

其中，t=1,2,…,T。

接着,构造如下的拉格朗日函数Lτ:

(8)

其中,不同分位点下的拉格朗日乘子ατ t,ατ t*,ητ t,ητ t*≥0(t=1,2,…,T)。接下来,对函数Lτ中的ωτ、bτ、ξt、ξt*一次求偏导并令其等于0,得到(9)式:

(9)

将(9)式带入(8)式中,SVQR模型等价于如下形式:

(10)

(11)

其中,t=1,2,…,T;K(xt,xk)为核函数,在已有的文献中,核函数有多种,如多项式核、径向基核、Sigmoid核和Fouier核函数等,本文选取的高斯核函数为:

(12)

(13)

(14)

1.3 参数选择

(15)

1.4 模型评价

采用经验分位数风险(Risk)、均方根误差(root mean square error,RMSE)和平均绝对误差(mean absolute error,MAE)来衡量模型的预测精度,它们的定义如下:

(16)

(17)

(18)

1.5 模型预测

本文使用条件密度预测方法对模型效果进行预测,条件密度预测建立在条件分布预测的基础上,但是更容易辨别随机变量的分布特征。

首先,需要求得模型的条件分布预测结果,当τ在(0,1)上连续取值时,分位数曲线Q就是分布曲线函数F。由于

(19)

两边对τ求微分可得:

(20)

(21)

(19)式和(21)式中,F-1(τ)·Q(τ)为τ分位数,对(21)式所示方程进行条件化和关于τ离散化,即可得到条件密度预测结果。

2 数值模拟

2.1 数据生成过程

通过Monte Carlo模拟方法来比较SVQR模型与线性分位数回归(linear quantile regression,LQR)模型的有限样本表现。首先,生成100个训练集合和100个测试集数据,其中回归变量x为服从U(0,1)的均匀分布,而响应变量y可由如下函数生成:

7.牛腺病毒病。40℃以上高热稽留，食欲减少，腹泻，粪便带血及黏膜块，眼鼻分泌物增多，咳嗽，呼吸次数增加，引起出生犊牛的肺炎及肠炎，可致母畜流产，重者死亡。

(22)

其中,m(x)为给定的非线性函数;σ(x)为以线性形式递增的位置因子,两者具体形式如下:

(23)

(24)

经上述方式设定的误差项σ(x)ε是非独立同分布的,从而得到了存在异方差性的响应变量y。其次,考虑随机误差ε服从正态分布、t分布和卡方分布,即ε～N(0,1)、ε～t(3)和ε～χ2(3)。因此,在给定x下,y在τ分位点下条件分位数的真实值为:

(25)

2.2 模型估计与评价

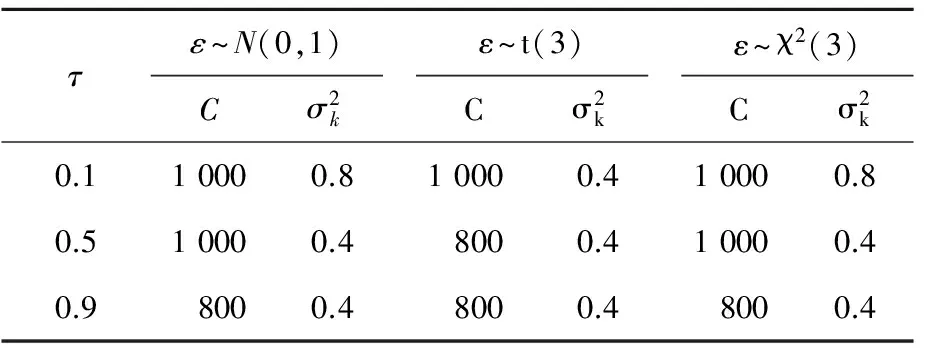
表1 SVQR模型在随机误差服从不同分布下各分位点上的最优参数

依次在0.1、0.5、0.9分位点下进行100次数值模拟实验,并将Risk、RMSE和MAE3个指标进行100次评价,结果的均值见表2所列。

表2 各评价指标在100个测试集中100次实验的均值

注:表中黑体数值表示各指标最小值时所选择的最佳模型。

从表2可知：

(1) 在ε～t(3)、ε～N(0,1)与ε～χ2(3)分布下,SVQR几乎所有的评价指标均小于LQR模型,表明SVQR模型较为优秀。

(2) 表中黑体数值显示,SVQR模型在绝大多数情况下均被选为最佳模型,具有很好的泛化能力。

2个模型更加详细的比较将以箱线图的形式展现出来,由于篇幅限制仅展示ε～N(0,1)分布下的比较结果,如图1所示。

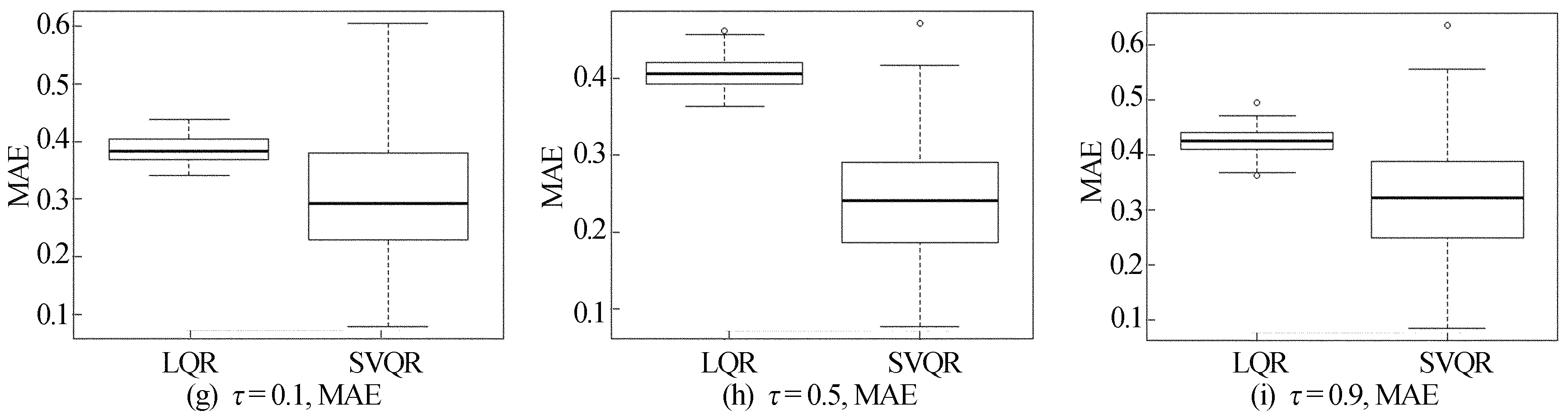
图1 LQR、SVQR模型在测试集随机误差ε～N(0,1)下各评价指标的箱线图

从图1可以看出,箱线图中的点显示出在绝大多数情况下SVQR模型更为出色。

3 实证研究

3.1 数据选取

为研究货币需求及其影响因素之间的关系,将货币需求划分为交易性需求、预防性需求和投机性需求3个层次。文献[13]认为这3个层次恰好为寻找引起货币需求变动的影响因素提供依据。交易性货币需求的影响因素选用宏观经济总量(如工业增加值、GNP、GDP等)作为代表,预防性货币需求的影响因素选用价格水平(如CPI)作为代表,投机性货币需求选用金融资产之间的替代关系(如金融资产价格、汇率、利率等)作为代表。文献[14]提出,汇率与股票价格对货币需求影响并不十分显著。因此,本文选取GDP、CPI与利率分别作为3个货币需求影响因素的代表。

考虑到月度数据相比年度数据更能揭示货币

需求变动细节,本文选取2004年1月至2014年12月总共132个月度数据作为研究对象。数据来源于国研网、中华人民共和国国家统计局与中国人民银行官方网站。

实证研究中,根据文献[15-17]的建议,M1与M2都可以作为货币研究目标,本文选择M1作为研究对象;由于GDP没有相关月度数据,改用工业增加值作为宏观经济总量的代表;利率则采用全国银行间同业拆借市场交易期限为7 d加权平均短期利率的月度数据。

3.2 货币需求函数分析

表3 SVQR模型参数选择结果

最后,通过Risk、RMSE与MAE 3个指标,将LQR模型与SVQR模型进行拟合效果比较,结果见表5所列。

表4 LQR模型回归系数估计及显著性检验

注:表中***、**分别表示1%和5%显著性水平下显著。

表5 SVQR模型与LQR模型评价结果

由表5可知,对任意分位点τ,SVQR模型的指标值都比LQR模型要小,表明SVQR模型能够更好地揭示货币需求系统的非线性动态特征。

3.3 货币需求条件密度预测

为使用已经建立的SVQR模型对2015年下半年的货币需求量M1进行条件密度预测,需要进行情景设置。据新浪财经报道,新华社发布消息称我国2015年工业增长值的增长目标为8%。另外据人民网报道,工信部发布消息称CPI增长目标将控制在3%左右,利率的增长目标约为0.05%,而M1的增长目标为10.6%。据此,本文假设工业增加值的增长率为2种情景:7.0%和9.0%;CPI的增长率为2种情景2.0%和4.0%;而利率增长率仅假设为0.05%。这样,可以划分4种情景,对解释变量进行设置,结果见表6所列。

根据表6的4种情景,分别对其做条件密度预测,情景1至情景4所得的条件密度预测结果如图2所示。

图2 概率密度函数

图2中,实线代表理论上的真实值,其数值大小根据2014年相对应的M1的月度数据与人民网上所获得M1的10.6%增长目标相乘所得;4条不同类型的虚线分别代表4种情景下的条件概率密度预测值,由于4种情景设置相差不多,因此4种情景对应的概率密度曲线变化走势相近。

从图2可以发现,6个月度的M1的条件密度预测结果图形状相似,但是均具有细微差别。另外还可以看出,使用SVQR模型方法能够获得M1完整概率分布特征的预测结果,且理论真实值也出现在密度函数之中。进一步观察可以发现,下半年6个月的月度数据除12月的预测值分布离理论真实值较远、理论真实值出现在条件概率密度函数的尾部以外,其余几个月条件概率密度预测值大多集中于M1理论真实值附近,这表明以较高概率出现的M1预测值与理论真实值几乎相同。

表6 宏观经济变量情景设置 %

4 结 论

SVQR模型可以视为支持向量机+分位数回归,本文将其应用于货币需求分析领域,充分发挥支持向量机的非线性处理能力与分位数回归的完整分布特征刻画能力,一方面能够得到货币需求及其影响因素之间的非线性依赖关系,另一方面能够给出货币需求完整概率分布特征描述。实证研究结果表明,SVQR模型能够很好地揭示中国货币需求变动规律,准确地给出货币需求条件概率密度预测结果。这些研究结果对提高货币政策决策效率、增强我国货币政策前瞻性等具有一定的参考价值。

[1] 许承明,宋海林.我国货币市场非均衡及其动态调整速度的变化[J].金融研究,2002(12):78-84.

[2] 汪红驹.用误差修正模型估计中国货币需求函数:基于两阶段(1978-1993、1994-2004)的动态检验[J].世界经济,2002(5):55-61.

[3] 蒋瑛琨,赵振全,刘艳武.中国货币需求函数的实证分析[J].中国软科学,2005(2):24-33.

[4] 高云峰.金融发展中的货币需求稳定性研究：基于1994～2005年的协调分析[J].数量经济技术经济研究,2006(5):31-40.

[5] 康继军,傅蕴英,张宗益.中国经济转型与货币需求[J].经济学(季刊),2012，11(2):463-488.

[6] GUERRON-QUINTANA P A.Money demand heterogeneity and the great moderation[J].Journal of Monetary Economics,2009,56(2):255-266.

[7] 张代强,张屹山.前瞻性利率规则在我国的实证研究:基于分位数回归方法的变参数检验[J].数量经济技术经济研究,2008(10):119-129.

[8] 许启发,蒋翠侠.分位数局部调整模型及应用[J].数量经济技术经济研究,2011(8):115-133.

[9] YUAN M.GACV for quantile smoothing splines[J].Computational Statistics & Data Analysis,2006,50(3):813-829.

[10] TAKEUCHI I,FURUHASHI T.Non-crossing quantile regressions by SVM[C]//Proceedings of 2004 IEEE International Joint Conference on Neural Networks.[S.l.]:IEEE,2004:401-406.

[11] LI Y J,LIU Y F,ZHU J.Quantile regression in reproducing kernel Hilbert spaces[J].Journal of the American Statistical Association,2007,102(477):255-268.

[12] SHIM J,KIM Y,LEE J,et al.Estimating value at risk with semiparametric support vector quantile regression[J].Computational Statistics,2012,27(4):685-700.

[13] 杨小勇,龚晓莺.货币政策效果与货币需求构成的关系及政策建议[J].经济学动态,2010(8):50-54.

[14] 伍戈.中国的货币需求与资产替代:1994-2008[J].经济研究,2009(3):53-67.

[15] 万晓莉,霍德明,陈斌开.中国货币需求长期是否稳定?[J].经济研究,2010(1):39-54.

[16] 陈荣,梁昌勇,谢福伟.基于SVR的非线性时间序列预测方法应用综述[J].合肥工业大学学报(自然科学版),2013，36(3):369-374.

[17] 史金凤,刘维奇,杨威.基于分位数回归的金融市场稳定性检验[J].中国管理科学,2011,19(2):24-29.

[18] ZHOU W,HE J M,YU D J.Kernel density weighted method of obtaining the least square support vector machines weightes[J].Journal of Information & Computational Science,2012,9(5):1247-1255.

(责任编辑 张 镅)

Research on money demand conditional density prediction based on support vector quantile regression

XU Qifa1,2, YU Yihan1, JIANG Cuixia1

(1.School of Management, Hefei University of Technology, Hefei 230009, China; 2.Key Laboratory of Process Optimization and Intelligent Decision Making of Ministry of Education, Hefei University of Technology, Hefei 230009, China)

Considering the complex relationship between money demand and its influence factors, the nonlinear dependence between money demand and its influence factors is discussed based on the support vector quantile regression(SVQR) model, and a method of money demand conditional density prediction is proposed. The SVQR model is also compared to the traditional linear quantile regression(LQR) model. The empirical study is conducted based on the monthly data of three factors including industrial added value, consumer price index(CPI), interest rate and the monthly data of M1 from January 2004 to December 2014. The results show that the SVQR model not only can fit well money demand, but also can give accurate conditional density prediction results.

money demand; quantile regression; support vector quantile regression(SVQR); conditional density prediction; generalized approximate cross validation(GACV) criterion

2015-09-30

国家自然科学基金资助项目(71071087)

许启发(1975-),男,安徽和县人,博士,合肥工业大学教授,博士生导师.

10.3969/j.issn.1003-5060.2017.01.022

F224.0

A

1003-5060(2017)01-0121-07