含VSC-HVDC电网扰动后暂态频率解析模型

李生虎, 汪秀龙, 朱国伟， 张晓艳

(1.合肥工业大学 电气与自动化工程学院,安徽 合肥 230009; 2.国网安徽省电力公司 经济技术研究院，安徽 合肥 230061)

含VSC-HVDC电网扰动后暂态频率解析模型

李生虎1, 汪秀龙1, 朱国伟2， 张晓艳1

(1.合肥工业大学 电气与自动化工程学院,安徽 合肥 230009; 2.国网安徽省电力公司 经济技术研究院，安徽 合肥 230061)

通过附加频率控制,柔性直流输电(voltage source converter based high voltage direct current，VSC-HVDC)参与电网调频,其快速控制特性可改善调频效果。文章基于潮流模型,计及同步发电机转子运动方程及调速系统,推导发电机转速与负荷扰动关系;考虑VSC-HVDC附加有功-频率下垂控制,提出电网暂态频率解析模型。IEEE 14节点算例分析表明,VSC-HVDC确实可改善暂态频率;量化解析模型和时域仿真结果误差验证了前者的准确性;比较两者误差计算时间,验证解析模型计算效率;修改VSC-HVDC附加控制器参数,验证解析模型在不同运行条件下的适用性。

柔性直流输电(VSC-HVDC);暂态频率;解析算法;潮流;一次调频

频率是衡量同步电力系统电能质量指标之一。文献[1]提出常规电网暂态频率解析模型,快速量化有功扰动下的暂态频率;文献[2]建立风电波动时的暂态频率解析模型,在含有无穷大母线的电网中分析了有功缺额扰动下不同节点的频率波动变化;文献[3]考虑风电场并网的位置不同,建立风电功率扰动暂态频率的解析模型,对比频域、时域结果,验证模型的准确性。

柔性直流输电(voltage source converter based high-voltage direct-current,VSC-HVDC)解耦控制有功与无功,可实现无源逆变,能为无源网络供电;潮流反转时不改变电压极性,适合构成多端网络[4-6]，广泛应用于风电场并网[7-8]、电网暂态调频[9]等方面。改变VSC-HVDC接入点注入有功可调节电网频率。文献[10]将VSC-HVDC逆变侧等值为同步发电机,采用虚拟惯量控制,基于有功-频率下垂特性参与弱电网调频;文献[11]采用增量法计算弱电网扰动后有功缺额,通过增加VSC-HVDC传输有功,稳定电网频率;文献[12]基于VSC-HVDC进行风电场并网,依靠VSC-HVDC直流电容参与惯性调频。

针对以上文献所述VSC-HVDC调频能力及目前缺乏含VSC-HVDC频率解析计算的研究，本文采用同步发电机转子运动方程和计及调速系统,提出含VSC-HVDC电网暂态频率解析模型量化电网有功波动对系统各节点频率及发电机转速的影响，比较解析计算和时域仿真结果误差,检验算法的准确性和适用性。

1 系统线性化模型

以下研究有功对频率的影响,简化无功与电压,认为全网电压均为1 pu,忽略无功传输,VSC-HVDC实现功率解耦控制,仅考虑注入有功。

1.1 基于有功的线性潮流模型

对于含有N个发电机和M个负荷电网,暂态过程中平衡机组功角发生变化。电网中各角度仍可以此为基准,但若继续认为其值为0则等价于平衡机组转速不变,调速系统暂态过程不动作,有功出力对电网频率无响应,显然不妥。因此,若N#机组为平衡机组,各角度做如下变换

(1)

其中,δ、θ分别为发电机功角和负荷节点电压相角;α、β分别为等值后的功角和相角;i、j分别为发电机与负荷节点。

考虑到发电机模型计及转子运动方程,而负荷仅为静态,因此电网模型可以写为分块矩阵形

(2)

其中,P为节点注入有功向量;B为电纳矩阵;G、L分别为发电机和负荷节点。

1.2 同步发电机转子运动方程

考虑(1)式所作变换,保持平衡机组转子运动方程不变,非平衡机组方程形式如下

(3)

其中,ω0为额定电角速度,ω0=2πf0;f0为基准频率,f0=50 Hz;矩阵TJ=diag{TJi},D=diag{Di},其中TJi为第i台机组惯性时间常数,Di为机组阻尼系数;K为N-1维单位列向量。

同步发电机的调速系统图1所示。

图1 调速系统结构

图1中,Kδ为频率调节效应系数;Ts为调速器延时;TCH、TRH分别为高压蒸汽和中间再热蒸汽容积效应时间常数;α为高压缸稳态输出功率占汽轮机总输出功率的百分比。由此推导调速系统线性化方程为

(4)

其中,Ggov(s)为调速系统传递函数。

1.3 暂态频率计算

计及频率在空间上的差异,引入节点暂态频率计算公式[13]如下

(5)

将(1)式代入(5)式可得向量形式的频率模型如下

(6)

其中,C为M维单位列向量。

2 常规电网暂态频率表达式推导

根据有功线性潮流模型,计及发电机转子运动方程和调速系统推导不含VSC-HVDC电网在有功波动下各发电机转速计算表达式,并以此通过暂态频率计算公式建立电网暂态频率解析模型。由(2)式分别消去Δα、Δβ可得

(7)

考虑到负荷节点暂态频率的定义,由(7)式可得负荷节点电压相角表达式,即

Δβ=(H′-1-H′-1L′L)ΔPL-H′-1L′HΔα

(8)

单独考虑平衡机组,节点注入功率ΔPGN根据线性潮流模型写为矩阵形式,即

(9)

其中,bN为平衡节点自电纳;BN=[0 0 … -bN]。

将(8)式代入(9)式可得

(10)

为方便模型推导,整理(3)式可得N台发电机转子运动方程矩阵为：

(11)

将(8)式、(11)式代入(12)式消去ΔPG与ΔPGN可得:

(12)

其中,I(N-1)×(N-1)为N-1维单位对角阵。

将(13)式写为分块矩阵形式，即

(13)

其中,分块矩阵Δω′、ΔPm′、J、S、T、W分别对应(12)式中虚线分割的各部分。

为引入发电机调速系统,对(13)式做拉氏变换,即

(14)

利用(4)式消去(14)式中ΔPm′ (s),同时消去Δα(s),可得有功负荷波动时同步发电机转速的解析表达式,即

(15)

其中,Gω(s)=[sIN×N-S(sI(N-1)×(N-1))-1J-T-UGgov(s)]-1W,其中,Ggov(s)=diag{Ggovi(s)},Ggovi(s)为第i台发电机调速系统传递函数。

下面由发电机转速及暂态频率推导暂态频率解析模型。

将各发电机转子运动方程和(8)式代入(6)式可得:

(16)

若负荷节点有功扰动为阶跃变化,则除扰动时刻外dΔPL/dt≡0,(16)式可写为:

(17)

将(3)式及(15)式代入(17)式可得常规交流电网在有功负荷扰动下暂态频率解析模型,即

(18)

3 含VSC-HVDC电网暂态频率推导

3.1 暂态频率解析推导

直流输电线路两侧换流站分别采用定直流电压和定有功功率控制,在定有功控制器外环引入有功-频率下垂附加控制参与调频,传递函数如图2所示,图2中,RVSC为斜率;kp、ki为PI控制参数。

图2 VSC附加频率外环控制器

考虑到换流器响应时间短[14-15],将注入有功对频率的响应视为一阶惯性环节,即

(19)

换流站交流母线注入有功可视为负的负荷,(18)式可写为:

(20)

将(19)式代入(20)式并化简,得到含VSC-HVDC电网在有功负荷扰动时的暂态频率解析模型,即

(21)

其中,Gf′(s)=[IM×M+Gf(s)GVSC(s)]-1Gf(s)。

3.2 误差指标

为评估所提解析模型计算相对于时域仿真结果的准确程度,采用平均相对误差[16](average relative error, ARE)和最大相对误差(maximum relative error, MRE)量化两者偏离程度,具体计算公式为:

(22)

(23)

其中,Δf(k)、Δfc(k)分别为k时刻时域仿真与解析计算得到的频率偏差量。

4 算例分析

改进的IEEE 14节点系统如图3所示。

图3 改进的IEEE 14节点系统

采用该系统[17]验证模型准确性,其中20#发电机为平衡机组。线路6至线路15改造为VSC-HVDC线路,节点15处换流站采用定直流电压控制,节点6处换流站采用定有功控制并附加图2所示频率下垂控制器,频率信号引自负荷节点6。VSC-HVDC参数见表1所列。

算例中设置扰动均为在t=0.1s时,节点6有功负荷增加7.5MW,考虑到负荷点对频率要求较高且为使计算结果反映全网频率情况,选取图3中4、5、13、14负荷节点进行分析。解析计算与时域仿真均在配置为3.2GHzIntel(R)Core(TM)i5 处理器,4GB内存的台式计算机上采用Matlab编程完成,时域仿真步长取为0.01s,收敛精度为10-6。

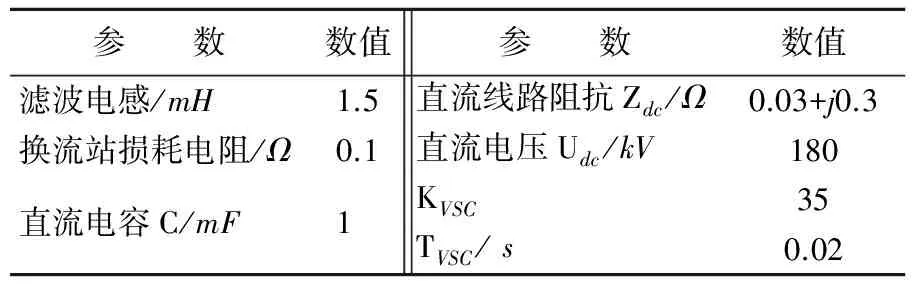
表1 VSC-HVDC参数表

4.1 VSC-HVDC调频效果分析

线路6至线路15为交流线路和VSC-HVDC线路时,负荷节点6的频率时域仿真曲线如图4所示。由图4可知,VSC-HVDC线路可改善电网调频效果:频率跌落最低点更浅,跌落后恢复较快。由于VSC-HVDC的快速功率调节特性,能够更快响应电网频率。

图4 节点6频率时域仿真曲线

4.2 交流电网暂态频率

系统中部分节点频率解析计算与时域仿真结果误差曲线如图5所示,误差指标见表2所列。

由图5可知,在扰动初期频率振荡最剧烈时,模型绝对误差可达10-5pu,稳态则在10-6pu,计算精度得以保证。ARE与MRE均在10-2数量级,验证解析模型的准确性。时域仿真所需时间为25.1 s,解析模型仅需2.1 s,降低了91.6%的计算时间。

图5 不含VSC-HVDC负荷节点频率绝对误差

节点编号451314ARE1．91101．90071．83781．8456MRE8．79497．86859．24199．8204

4.3 含VSC-HVDC电网节点频率对比

含VSC-HVDC电网暂态频率绝对误差如图6所示，各负荷节点频率误差见表3所列。ARE与MRE均在10-2数量级。时域仿真时间为31.6 s,解析模型计算时间为6.2 s,降低了80.4%。

图6 含VSC-HVDC负荷节点频率绝对误差

表3 含VSC-HVDC负荷节点频率误差 10-2

节点编号45610ARE1．34371．31221．30331．3036MRE7．79126．87546．35445．9587

4.4 控制参数分析

改变VSC-HVDC控制参数KVSC及TVSC时,负荷节点6频率跌落时域仿真曲线如图7所示。

图7 变参数下节点6频率跌落时域仿真曲线

由图7可知,增益系数变化对电网暂态频率影响较大,而时间常数几乎不对其产生影响。解析计算绝对误差曲线如图8所示。

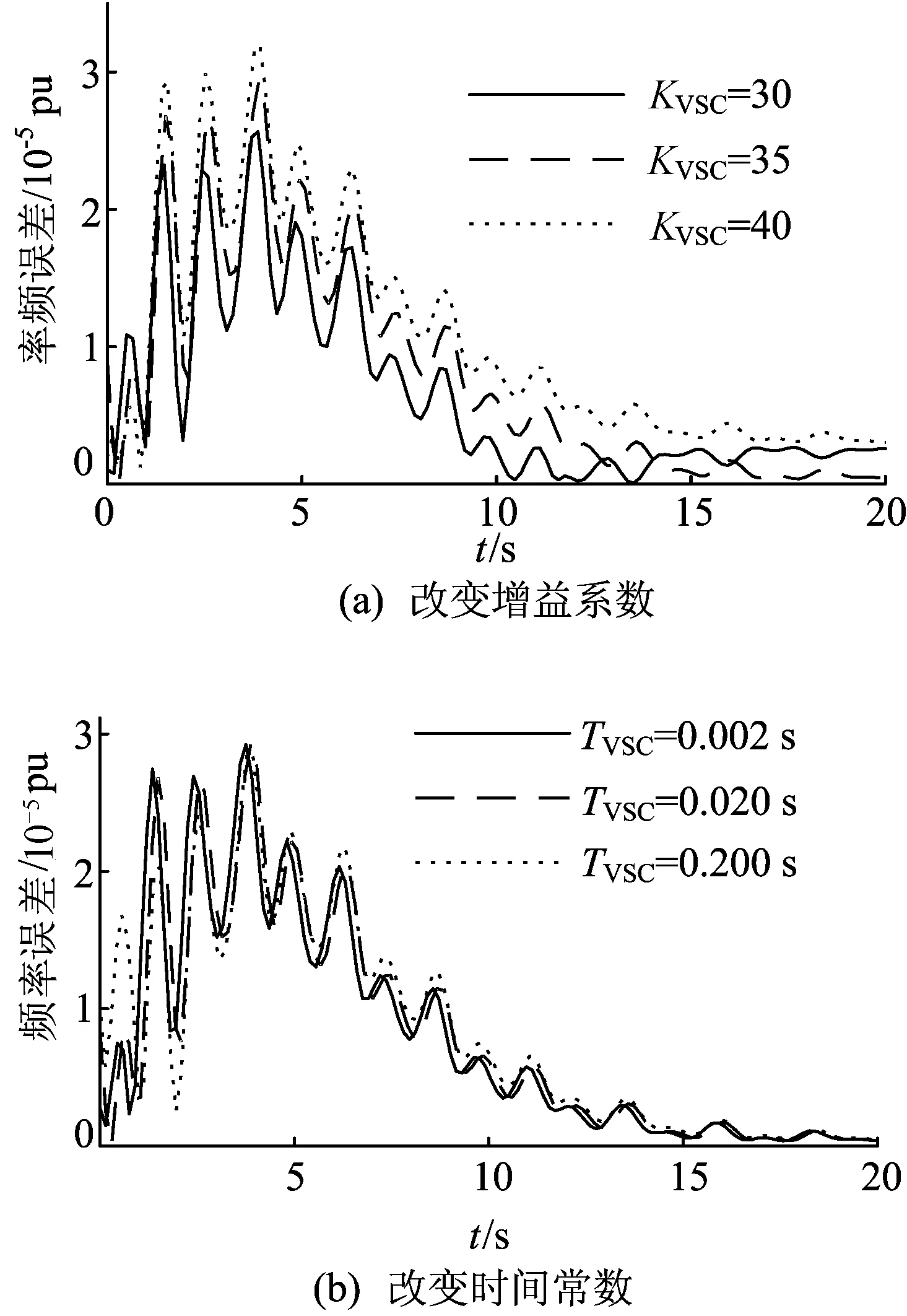
图8 变参数下节点6频率绝对误差

误差指标及计算时间见表4所列。解析模型在变参数情况下,保证4.3节计算时间的同时仍可达到相近的频率计算精度。

表4 节点6变参数频率误差指标及时间

5 结 论

本文计及发电机转子运动方程及调速系统,提出了含VSC-HVDC电网的扰动后暂态频率解析模型,得到以下结论:

(1) 相比常规交流线路,VSC-HVDC线路的快速功率特性有助于实现更优调频效果。

(2) 与时域仿真相比,所提解析模型计算时间显著降低,误差较小,有助于评估含VSC-HVDC大规模电网暂态频率。

(3) 模型可以通过修改直流部分传递函数参数，应用于含有多个直流注入节点电网暂态频率的计算。

[1] 李常刚，刘玉田，张恒旭，等.基于直流潮流的电力系统频率响应分析方法[J].中国电机工程学报，2009，29(34):36-41.

[2] 林今，孙元章，李国杰，等.采用变速恒频机组的风电场有功功率波动对系统节点频率影响的动态评估模型[J].电力自动化设备，2010，30(2):14-18.

[3] 徐箭，施微，徐琪.含风电的电力系统动态频率响应快速评估方法[J].电力系统自动化，2015，39(10):22-27.

[4] 徐政.柔性直流输电系统[M].北京:机械工业出版社，2013.

[5] 朱代祥，丁明.基于内模控制的 VSC-HVDC 系统仿真研究[J].合肥工业大学学报(自然科学版)，2010，33(5):652-656.

[6] 吴红斌，丁明.轻型直流输电系统动态特性的电磁暂态仿真[J].合肥工业大学学报(自然科学版)，2007，30(1):41-44.

[7] 陈树勇，徐林岩，孙栩，等.基于多端柔性直流输电的风电并网控制研究[J].中国电机工程学报，2014，34(增刊1):32-38.

[8] 潘伟，李勇，曹一家，等.用于大规模集中式风电并网的 VSC-HVDC 频率控制方法[J].电力自动化设备，2015，35(5):94-99.

[9] 李生虎，鲍正杰，董王朝，等.基于直流电容充放电双阈值判据的VSC-HVDC区域电网频率控制方法[J].电力科学与技术学报，2014，29(3):26-32.

[10] 唐欣,张武其,陈胜，等.与VSC-HVDC连接的弱电网暂态频率偏移定量计算和调整方法[J].中国电机工程学报，2015，35(9):2170-2176.

[11] 鲍正杰，李生虎.基于VSC-HVDC有功支援和自适应低频减载的区域电网频率控制[J].电力系统保护与控制，2014，42(20):32-37.

[12] PIPELZADEN Y，JUNYENT-FERRE′ A，GREEN T C.Blending HVDC-link energy storage and offshore wind turbine inertia for fast frequency response[J].IEEE Trans on Sustainable Energy，2015，6(3):1059-1066.

[13] 韩英铎，闵勇.复杂扩展式电力系统功率频率动态过程分析[J].电力系统自动化，1992，16(1):28-33.

[14] 刘栋，汤广福，郑健超，等.模块化多电平换流器小信号模型及开环响应时间常数分析[J].中国电机工程学报，2012，32(24):1-7.

[15] 金辰璐，张兴，周岩峰.模块化多电平变换器与三电平变换器于低压光伏并网系统的应用对比[J].合肥工业大学学报(自然科学版)，2014，37(5):543-550.

[16] 雷庆坤，李生虎，陈曦鸣，等.基于改进的LMD和GRNN组合风速预测[J].合肥工业大学学报(自然科学版)，2015，38(7):891-896.

[17] University of Washington.Power System Test Case Archive [EB/OL].[2016-01-07].http://www.ee.washington.edu/research/pstca/.

(责任编辑 张 镅)

Analytical model of post-fault transient frequency in power system with VSC-HVDC

LI Shenghu1, WANG Xiulong1, ZHU Guowei2， ZHANG Xiaoyan1

(1.School of Electric Engineering and Automation, Hefei University of Technology, Hefei 230009, China; 2.Economy and Technology Research Institute, State Grid Anhui Electric Power Company, Hefei 230061, China)

With additional frequency controller, the voltage source converter based high-voltage direct-current(VSC-HVDC) may participate in system frequency regulation, whose fast control improves frequency regulation effect. Based on power flow model and including the motion equation and governor system of the synchronous generators, the rotor speed following load disturbance is derived. Based on the power-frequency droop control to VSC-HVDC, the analytical model to quantify the transient frequency of power system is proposed. The numerical results on IEEE 14-bus test system show that the VSC-HVDC helps to improve the transient frequency; accuracy of the analytical model is validated by quantifying its error with the time-domain results; efficiency of the analytical model is validated by comparing the calculation time of both models; feasibility of the analytical model under various operational conditions is validated by changing the control parameters of the VSC-HVDC.Key words:voltage source converter based high-voltage direct-current(VSC-HVDC); transient frequency; analytical model; power flow; primary frequency regulation

2015-10-29；

2016-03-10

国家自然科学基金资助项目(51277049)

李生虎(1974-),男,安徽合肥人,博士,合肥工业大学教授,博士生导师.

10.3969/j.issn.1003-5060.2017.01.009

TM614

A

1003-5060(2017)01-0047-06