环F2+uF2+vF2+uvF2上的(1+u+v)-常循环码

缪 扬, 刘 丽

(合肥工业大学 数学学院,安徽 合肥 230009)

环F2+uF2+vF2+uvF2上的(1+u+v)-常循环码

缪 扬, 刘 丽

(合肥工业大学 数学学院,安徽 合肥 230009)

文章研究了环R=F2+uF2+vF2+uvF2上的(1+u+v)-常循环码，定义了一个Gray映射,证明了该环上的(1+u+v)-常循环码的Gray像是等距的准循环码,并利用该映射得到了二元好码,进一步确定了任意长度该常循环码的结构,同时也讨论了它的对偶码。

常循环码;生成多项式;Gray映射;Gray距离;对偶码

文献[1]证明了一些好的二元非线性码可以看作是环Z4上循环码的Gray像。自此,有限环上码的研究引起了很多学者的兴趣。文献[2-3]分别用不同的方法研究了环Zpm上循环码的结构;文献[4]研究了环Zm上任意长度的循环码;文献[5-7]讨论了环F2+uF2上的线性码、循环码及其对偶码,并且得到了二元最优码;文献[8]得到了环F2+uF2上单根(1+u)-常循环码的Gray像是距离不变的二元循环码;文献[9]研究了有限链环上的循环码和负循环码,并给出了该环上循环码的结构;文献[10]研究了环Fp[u]/〈um〉上任意长度的(1+λu)-常循环码,给出了该常循环码的结构,同时得到了一些二元好码;文献[11]研究了环F2+uF2+…+ukF2上的循环码和(1+uk)-常循环码。但是这些文献都是基于有限链环上的研究。

最近,文献[12-13]研究了环F2+uF2+vF2+uvF2上的线性码和循环码,并通过Gray映射得到了一些好的二元码。由于环F2+uF2+vF2+uvF2是非链环,因此用于研究该环上码的方法与有限链环中的方法不同。文献[14]研究了环F2+uF2+vF2+uvF2上奇长度的(1+v)-常循环码。

本文在上述研究基础上研究了环R=F2+uF2+vF2+uvF2上任意长度的(1+u+v)-常循环码,其中u2=v2=0,uv=vu。证明了环R上长为n的(1+u+v)-常循环码C在Gray映射下的像φ(C)是等距的准循环码,并给出了一个通过该映射找到二元好码的例子,同时确定了环R上(1+u+v)-常循环码的结构。

1 预备知识

环R=F2+uF2+vF2+uvF2是特征为2的有限交换环,其中u、v满足u2=v2=0,uv=vu。显然R是局部环但不是主理想环,它的唯一极大理想为:

I={0,u,v,u+v,uv,u+uv,

v+uv,u+v+uv}

(1)

R上长为n的码是Rn的一个非空子集,若它还是Rn的一个R-子模,则称其为线性码。对于R上单位λ和长为n的线性码C,若对任意码字c=(c0,c1,…,cn-1)∈C,均有它的λ-常循环移位τλ(c0,c1,…,cn-1)=(λcn-1,c0,…,cn-2)∈C,则称C为λ-常循环码。

对于C中任意码字c=(c0,c1,…,cn-1),可以用R[x]上的多项式来表示,即

(2)

这样R上长为n的λ-常循环码亦即R[x]/〈xn-λ〉的理想。特别地,若λ=1,称C是R上的循环码。

令x=(x0,x1,…,xn-1),y=(y0,y1,…,yn-1)为Rn中2个元素,x与y的内积定义为[x,y]=x0y0+x1y1+…+xn-1yn-1,C的对偶码C⊥={x∈Rn|[x,y]=0,∀y∈C}。若C⊆C⊥,称C为自正交码;若C=C⊥,称C为自对偶码。

2 Gray映射

定义1 对任意的r∈R,有

r=a+ub+vc+uvd

(3)

φ(a+ub+vc+uvd)=

(4)

(5)

(6)

引理1 设φ为定义1中的Gray映射,τ为Rn上的(1+u+v)-常循环移位,则φτ=σ2φ。

证明 设r=(r0,r1,…,rn-1)∈Rn,ri=ai+ubi+vci+uvdi,其中，ai、bi、ci、di∈F2；0≤i≤n-1。由定义1有:

(7)

因此有：

(8)

另一方面,

a0+ub0+vc0+uvd0,…,

(9)

因此有：

(10)

故φτ=σ2φ。

定理1R上长为n的码C是(1+u+v)-常循环码的充要条件是其Gray像φ(C)是长为4n、指数为2的二元准循环码。

证明 设C为R上的(1+u+v)-常循环码,由引理1可知，σ2(φ(C))=φ(τ(C))=φ(C)。因此,φ(C)是长为4n、指数为2的二元准循环码。

设φ(C)是长为4n、指数为2的二元准循环码,由引理1有:

(11)

由于φ是单射,因此τ(C)=C,即C是环R上的(1+u+v)-常循环码。

定理2 设C是R上长为n的(1+u+v)-常循环码,则有φ(C⊥)=φ(C)⊥。

证明 设

r1=a1+ub1+vc1+uvd1,

r2=a2+ub2+vc2+uvd2∈Rn

(12)

若[r1,r2]=0,则有：

(13)

因此有：

(14)

故φ(C⊥)⊆φ(C)⊥。

另一方面,因为R是Frobenius环,所以|C||C⊥|=24n。又因为φ为双射,所以有：

从而有：

故可得到φ(C⊥)=φ(C)⊥。

推论1C为R上自对偶码的充要条件是φ(C)为F2上的自对偶码。

3 R上的(1+u+v)-常循环码

首先,本文考虑环F2+uF2上的(1+u)-常循环码,然后借助该结构来考虑环R上的(1+u+v)-常循环码。设n=2km,其中m是奇数,记

S=F2+uF2，

(15)

则S上长为n的(1+u)-常循环码是Sn的理想。

对于S上长为n的线性码C,定义如下与其密切相关的2个长为n的二元线性码。

挠码:

(16)

剩余码:

(17)

引入映射υ:C→Res(C)定义为υ(a+ub)=a,显然有:

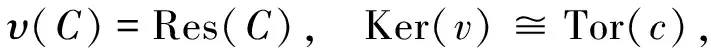
(18)

(19)

其中,hi=min{2k,ki};li=ki-min{2k,ki}。

引理4[10]设C是S上长为n的(1+u)-常循环码,d1、d2分别为其剩余码和挠码的极小Hamming距离。若d1≥2d2,则C的Gray距离为2d2。

本文考虑R上(1+u+v)-常循环码的结构。设Rn=R[x]/〈xn-(1+u+v)〉,则R上长为n的(1+u+v)-常循环码可以视作Rn的理想。对于R上长为n的线性码C,同样地定义它的换码与剩余码。

挠码:

Tor(C)={x∈Sn|vx∈C}

(20)

剩余码:

(21)

考虑映射φ:R→S,定义为:

φ(a+ub+vc+uvd)=a+ub

(22)

将其扩展到多项式环上得到映射Rn→Sn,即

(23)

将φ限制在C上,则有φ:C→Res(C),φ(a+vb)=a,其中，a、b∈Sn。同理有:

Ker(φ)≌Tor(C),

(24)

定理3 设f(x)∈F2[x]整除x2n-1,h(x)=(x2n-1)/f(x)。若C是R上长为n的(1+u+v)-常循环码,则

(25)

其中,g(x)|f(x)|(x2n-1);g(x)|[p(x)+(xn-1)q(x)]h(x)。

且

deg(g(x))>deg(p(x)),

deg(g(x))>deg(q(x))。

证明 设xm-1=f1(x)f2(x)…fr(x),其中fi(x)是F2[x]中两两互素的首一不可约多项式。设C是R上长为n的(1+u+v)-常循环码,C在φ下的像是Sn的理想,由引理2可知：

其中，p(x),q(x)∈F2[x]。

显然可以做如下假设：

deg(g(x))>deg(p(x)),

deg(g(x))>deg(q(x))。

(26)

故g(x)|[p(x)+(xn-1)q(x)]h(x)。

另一方面,

(27)

故g(x)|f(x)。

定理4 设C=〈f(x)+vp(x)+uvq(x),vg(x)〉是R上长为n的(1+u+v)-常循环码,其中f(x),g(x),p(x),q(x)的定义如定理3,则有：

推论2 设C是R上长为n的(1+u+v)-常循环码,d1、d2分别为Res(C)和Tor(C)的极小Lee距离,若d1≥2d2,则C的Gray距离是2d2。

证明 任意的非零码字c∈C,若其分量具有形式c=a+vb,其中a∈S{0},b∈S,则φ(C)∈Res(C),故wG(C)≥d1。另一方面,若c=vb,b∈Sn, 则c必在vTor(C)中。根据Gray映射的定义,c的Gray重量是2wL(c)。故若d1≥2d2,则dG(C)=2d2。

定理5 设C是R上的长为n的(1+u+v)-常循环码,则它的对偶码C⊥也是R上的(1+u+v)-常循环码。

证明 设(a0,a1,…,an-1)∈C⊥,对∀ (c0,c1,…,cn-1)∈C,有

(28)

则

(1+u+v)c1a0+(1+u+v)c2a1+

(29)

(29)式两边同乘以1+u+v得:

(30)

所以((1+u+v)an-1,a1,…,an-2)∈C⊥,故C⊥是(1+u+v)-常循环码。

在定理3中令p(x)=q(x)=0,此时C=〈f(x),vg(x)〉,其中f(x)|(x2n-1),g(x)|f(x)。注意到S是R的子环,故Res(C)=〈f(x)〉是C的子码。

vTor(C)=v〈g(x)〉包含于C,故此时C的Gray距离为min{d1,2d2},其中d1、d2分别为其剩余码和挠码的极小Lee距离。

推论3 设C=〈f(x),vg(x)〉是R上长为n的(1+u+v)-常循环码,其中f(x)|(x2n-1),g(x)|f(x),则C的Gray距离为min{d1,2d2},其中d1、d2分别为Res(C)和Tor(C)极小Lee距离。

例1 考虑R上长为6的(1+u+v)-常循环码。在F2[x]中,x12-1=(x-1)4(x2+x+1)4。

令f(x)=(x-1)3(x2+x+1)4,g(x)=(x-1)(x2+x+1)4,则有:

vx5+vx4+(v+uv)x3+

(v+uv)x2+vx+v〉

(31)

(31)式是R上长为6的(1+u+v)-常循环码。由定理4知,Res(C)=〈(x-1)3(x2+x+1)4〉是S上长为6的(1+u)-常循环码,参数为[6,2,12];Tor(C)=〈(x-1)(x2+x+1)4〉是S上长为6的(1+u)-常循环码,参数为[6,23,6];又由推论3知,C的Gray像φ(C)是参数为[24,4,12]的二元准循环码,它是最优二元码。

4 结 论

本文研究了环R=F2+uF2+vF2+uvF2上的(1+u+v)-常循环码的Gray映射及其性质,并利用映射构造出二元好码,确定了R上任意长度的(1+u+v)-常循环码结构。还有很多有意义的问题有待研究,比如考虑该环上其他类型的常循环码或者研究更一般的环R=Fq+uFq+vFq+uvFq(q是奇素数的幂)上常循环码的问题。

[1] HAMMONS A R，Jr,KUMAR P V，CALDERBANK A R，et al.TheZ4-linearity of kerdock，preparata，geothals and related codes[J].IEEE Trans Inform Theory，1994，40(4)：301-319.

[2] CALDERBANK A R，SLOANE N J A.Modular andp-adic cyclic codes [J].Designs，Codes and Cryptography，1995，6(1)：21-35.

[3] KANWAR P，LóPEZ-PERMOUTH S R.Cyclic codes over the integers modulopm[J].Finite Fields Appl，1997，3(4)：334-352.

[4] DOUGHERTY S T，PARK Y H.On modular cyclic codes [J].Finite Fields and Their Applications,2007,13:31-57.

[5] BONNECAZE A，UDAYA P.Cyclic codes and self-dual codes overF2+uF2[J].IEEE Transactions on Information Theory,1999,45(4):1250-1255.

[6] 余海峰,朱士信.环F2+uF2上线性码及其对偶码的二元象[J].电子与信息学报,2006，28(11)：2121-2123.

[7] 李平,朱士信.环F2+uF2上长为2e的循环码[J].电子与信息学报,2007，29(5)：1124-1126.

[8] QIAN J F，ZHANG L N，ZHU S X.(1+u)-constacyclic and cyclic codes overF2+uF2[J].Applied Mathematics Letters，2006，19(8)：820-823.

[9] DINH H Q,LóPEZ-PERMOUTH S R.Cyclic and negacyclic codes over finite chain rings[J].IEEE Transactions on Information Theory，2004,50(8):1728-1744.

[10] KAI X S，ZHU S X，LI P.(1+λu)-Constacyclic codes overFp[u]/〈um〉[J].Journal of the Franklin Institute,2010，347(5)：751-762.

[11] 王玉.环F2+uF2+…+ukF2上的循环码和(1+uk)-循环码[J].合肥工业大学学报(自然科学版),2009,32(7):1117-1120.

[12] YILDIZ B,KARADENNIZ S.Linear codes overF2+uF2+vF2+uvF2[J].Des Codes Cryptogr，2010,54:61.

[13] YILDIZ B,KARADENNIZ S.Cyclic codes overF2+uF2+vF2+uvF2[J].Des Codes Cryptogr，2011，58:221-234.

[14] KARADENNIZ S，YILDIZ B.(1+v)-constacyclic codes overF2+uF2+vF2+uvF2[J].Journal of the Franklin Institute,2011,348(9)：2625-2632.

(责任编辑 闫杏丽)

(1+u+v)-constacyclic codes over ringF2+uF2+vF2+uvF2

MIAO Yang, LIU Li

(School of Mathematics, Hefei University of Technology, Hefei 230009, China)

In this paper, the (1+u+v)-constacyclic codes over the ringR=F2+uF2+vF2+uvF2are discussed. Firstly, a Gray map ofCis defined and it is proved that under this map the Gray image ofCoverRis a binary distance invariant quasi-cyclic code. And their dual codes are discussed. Then a set of generators of such constacyclic codes for an arbitrary length is determined. Finally, an optimal binary code is obtained from the Gray map.

constacyclic code; generator polynomial; Gray map; Gray distance; dual code

2015-05-07

国家自然科学基金资助项目(11201107;11401154)

缪 扬(1991-),男,安徽合肥人,合肥工业大学硕士生; 刘 丽(1965-),女,安徽枞阳人,博士, 合肥工业大学教授,硕士生导师.

10.3969/j.issn.1003-5060.2017.01.025

TN911.22

A

1003-5060(2016)12-0140-05