考虑产品变质的生产与分车联合优化调度问题研究

马 英, 马晶晶, 李 凯

(1.合肥工业大学 管理学院,安徽 合肥 230009; 2.合肥工业大学 过程优化与智能决策教育部重点实验室,安徽 合肥 230009)

考虑产品变质的生产与分车联合优化调度问题研究

马 英1,2, 马晶晶1, 李 凯1,2

(1.合肥工业大学 管理学院,安徽 合肥 230009; 2.合肥工业大学 过程优化与智能决策教育部重点实验室,安徽 合肥 230009)

文章研究了冷链环境中单机生产模式下多订单的生产与分车问题,即生产商为客户生产多个订单并分配车辆为客户配送。由于产品为易变质产品,随着时间的推移会产生变质成本,且配送存在车辆使用成本,因此需要合理安排生产计划及分车方案,以便使得车辆成本与产品变质成本之和最小化。文章首先进行问题分析,提出几条最优解的性质,在此基础上构造2个算法,进而提出问题的一个下界,并通过大规模实验验证算法的有效性。

生产;分车;联合调度;易变质产品;单机

0 引 言

关于冷链型企业所生产的易变质产品的研究大多聚焦库存控制、经济批量等问题,如文献[1]研究了基于产品变质和零售商部分延期支付的经济订货批量(economic order quantity,EOQ)模型,但是涉及生产调度和供应链调度方面的研究文献相对较少。随着供应链管理理论的发展,人们逐渐认识到供应链中各个环节的有效配合才能发挥最大功用,特别是对于冷链型企业,其时效性要求冷链各环节具有更高的组织协调性,因此冷链型企业资源调度问题逐渐成为供应链管理和生产调度领域的一个热点和前沿问题。

文献[2]最早提出了分车配送问题,研究了单机生产模式下使总加权提前惩罚与配送成本最小化问题;文献[3]论证了此问题可转化为经典平行机调度问题,并且可将解决平行机调度问题的方法直接应用于解决该问题。之后,许多学者在文献[2]研究的基础上进行了拓展,文献[4]考虑了配送成本是每车订单数量的线性增函数,且车辆数是有限制的；文献[5]考虑了一种更复杂的情况,目标函数由提前与延迟惩罚、库存和配送成本构成；文献[6]在多周期随机需求下研究了供应链库存与配送的联合优化模型；文献[7]研究了订单带交货期时间窗的情况,使包括提前、延迟、库存和配送成本在内的总成本最小化。目前,分车配送研究的共同点如下：① 车辆配送的起始时间等于该车最后一个加工订单的完工时间; ② 配送成本是使用车辆数的非减函数; ③ 车辆是没有容量限制的。然而以上文献均未涉及冷链型企业易变质产品问题的研究。

目前,学术界对于易变质产品生产与分车配送的研究并不多。文献[8]研究了具有保质期的单一产品由单一车辆配送问题，并且假设生产序列与配送序列是固定且相同的;文献[9]在文献[8]固定交付顺序问题的基础上做了进一步研究,对其提出的分支定界算法做了修正,解决了在产量和配送条件有限的情形下最大限度地满足客户需求问题;文献[10]研究了批量生产易变质产品的问题,并且在产品变质的前提下证明了批量有利于降低生产设置成本及配送成本,从而达到降低总成本的目的。文献[8-10]并没有考虑到产品持续性变质的情况,考虑的产品变质特性均体现在产品的保质期上,即某一产品一旦生产完成后经过一段固定的时间,产品就会变质不可用,在到达保质期之前,产品性状是不发生变化的,但是在现实中许多产品是持续性变质的,而保质期无法体现这一特性。针对这一问题,文献[11]考虑了产品变质率为常数的情况下,每个时段内产品的需求量是已知的,决定每个时段产品的生产量及生产顺序,满足需求并且使总成本最小化;文献[12]研究了单一生产线生产变质率为常数的易变质产品并配送给多个零售商的问题,企业需要确定每种产品的生产数量、开始生产时间以及产品的配送路线,其优化的目标是使企业期望总收益最大化;文献[13]研究问题的假设条件与文献[12]相同,也考虑了变质成本,只是其优化的目标是使期望总成本最小化;文献[14]把研究推广到了更复杂的生产环境,假设企业内有多条生产线,客户订单要求每种产品数量是固定的,并且产品之间存在与顺序相关的调整时间和调整成本,但是没有考虑到车辆使用的固定成本以及车辆的容量限制,事实上在现实中使用车辆时通常会有一定的启动成本,车容量也是有限制的,即只能容纳一定体积的产品。

本文研究了冷链环境下单一生产商为客户生产多订单的生产与分车问题,车辆有固定的容积限制,通过合理安排订单生产顺序及订单分车方案,使车辆成本和产品变质成本达到最小,从而降低生产商的成本。针对该问题,本文提出了解决方法,通过与下界比较证明了其有效性。

1 问题描述及分析

1.1 问题描述

在该问题中只有1个生产商,在1个调度周期初共有n个订单Jj(j=1,2,…,n)构成了1个作业集合,每一个周期内的订单只来自于同一个客户。

本文考虑的是单机生产模式,订单Jj的加工时间为pj(pj>0),体积为vj,产品呈线性变质,且变质率为uj,产品一旦生产完成后便开始变质,变质后产品的体积并不发生变化,生产单位体积产品需耗费的资源价值为mj。在产品的生产过程中,机器在同一时刻只能加工1个作业,并且作业是不允许中断的。对于1个订单Jj,Cj与Rj分别为作业的完工时间和装车时间。生产商使用的车辆均是容量为Q的同型车,n个订单分装到不同车辆上,每辆车的装车时间为该车辆订单中最后1个加工订单的完工时间。每辆车都有相同的启动成本,设每辆车送货1次的成本为F,共使用K辆车,整个周期的车辆总成本为KF。假设产品的加工是匀速进行的,在1个订单中,先完成产品的变质时间大于后完成产品的变质时间,在单个订单加工过程中,该订单产品的平均变质体积为vjujpj/2。在整个调度问题中,订单Jj发生变质的产品体积为vjuj(Rj-Cj+pj/2)。本文考虑的发生变质产品的体积为vj′=vjuj(Rj-Cj+pj/2),这部分产品在交货时不可用,其耗费的资源成为一种浪费,先视为耗材成本,对于订单Jj,其耗材成本即为vj′mj。由于用于交货的产品量少于订单量,缺少的这部分产品产生相应的缺货成本vj′gj,其中gj为单位体积的缺货费用。缺货成本是由产品变质产生的,且单位体积产品的耗材费用与缺货费用均为常数,在此问题中,将耗材成本与缺货成本合并统称为变质成本,用lj表示单位体积产品的变质费用lj=mjgj,则订单Jj的变质成本即为vj′lj。生产订单量产品所耗费的资源价值为vjmj,这部分成本为固定成本,在此问题中不作考虑。

该生产与分车问题的目标是总成本的最小化,即有：

(1)

设Π为生产调度的订单加工顺序集合。π∈Π为某一调度方案,π={π(1),π(2),…,π(n)},其中π(j)为调度方案π中第j个生产的订单,生产结束时间为Cπ(j)。ψ∈Ψ为某一分车方案,ψ=[ψ(π(1)),ψ(π(2)),…,ψ(π(n))],其中,ψ[π(j)]表示装载的车辆。

设π(j)对应的车辆的作业集为Aπ(j)={π(i)|ψ(π(i))=ψ(π(j)),i=1,2,…,n};订单π(j)的装车时间为：

(2)

(3)

对于一个生产方案π和分车方案ψ,其使用的车辆数为K,则该生产与分车问题的协同优化目标为：

(4)

在该问题中,目的是找到最优的生产与分车方案π*和ψ*,其中车辆数为K*,使得目标函数最小化,则有：

(5)

1.2 问题分析

通过分析该协同调度问题最优解具有的特征,并根据解的性质提出有效的方法。

性质1 同一车辆的订单在生产过程中彼此相邻。

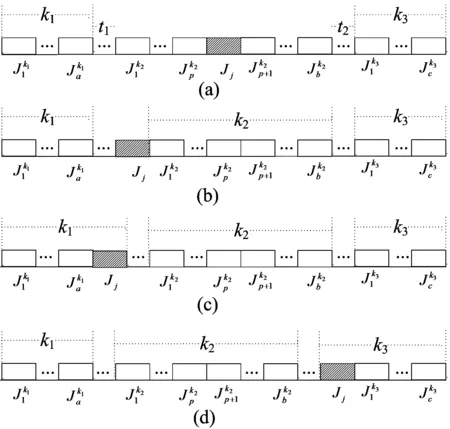
图1 最优解性质1的生产顺序

综上可知,当某一辆车上订单的生产序列中包含了非该辆车配送的订单时,均可以通过改变该订单的生产顺序使得目标函数减小,与最优解中必存在某辆车的订单不连续的假设相矛盾,因此假设不成立,则性质1是成立的。

性质2 每辆车上的订单生产顺序根据vjujlj/pj的值按照从小到大的规则排列。

图2 最优解性质2车辆k的订单生产顺序

设Δ为图2b所示生产顺序的变质成本减去图2a所示生产顺序的变质成本差值,则有：

(6)

性质3 以车辆为整体,每车订单的加工序列既定,改变整车订单加工的次序,不影响目标函数值。

证明略。目标函数不受每车订单的加工开始时间的影响,因此改变整车订单的加工次序不会对目标函数产生影响。

2 算法及下界

2.1 算法

根据性质1和性质2可知,若分车方案确定,生产的最优顺序是可以确定的,因此本文的生产与分车问题可以看作是求解最优分车方案。首先,固定容积的车辆,其使用数量必须满足装载全部订单的要求。由性质2可知,每辆车上先加工订单的vjujlj/pj值越小越好,因此考虑将vjujlj/pj值较小的订单分别排列在每辆车的前面加工。将所有的订单按照vjujlj/pj值从小到大排列,再从序列中的第1个订单开始,依次为其分配装载车辆。

车辆容积有限制,先分配的订单要尽可能地排列在每车订单中的前面,因此考虑在为每个订单分配车辆时,首先选择剩余容积最小的车辆,根据此原则构建剩余容积最小车辆优先算法。由于产品的易变质性与时间有很大的关系,在为每个订单分配车辆时,考虑选择已有订单加工时间和最小的车辆,根据该原则构建订单加工时间和最小车辆优先算法。

剩余容积最小车辆优先算法步骤如下：

(2) 车辆i(i=1,2,…,K)上装载的订单集合为Ki,Ki中所有订单的体积之和记为Vi,初始状态为Ki空集,Vi=0;将订单集合记作J,集合内所有订单按照vjujlj/pj值从小到大排列。

(3) 若J为空集,计算当前解的目标函数值,记为U′,若U′>U,则结束,返回U及其对应的集合Ki(i=1,2,…,K);若U′≤U,则令U=U′,K=K+1,返回到步骤(2)。

(4) 将J中第1个订单插入到Vi最小且插入后Vi≤Q的集合Ki中的最后一个位置,插入后将J中第1个订单剔除,执行步骤(3);若J中第1个订单找不到满足条件的集合Ki可以插入,则令K=K+1,返回到步骤(2)。

订单加工时间和最小车辆优先算法步骤为：

(3) 若J为空集,计算当前解的目标函数值,记为U′。若U′>U,则结束,返回及其对应的集合Ki(i=1,2,…,K);若U′≤U,则令U=U′,K=K+1,返回到步骤(2)。

剩余容积最小车辆优先算法与订单加工时间和最小车辆优先算法首先是将所有的订单按照vjujlj/pj值从小到大排列,再依次为每个订单分配装载车辆,剩余容积最小车辆优先算法分配车辆时,优先选择剩余容积最小的车辆,订单加工时间和最小车辆优先算法则优先选择订单加工时间和最小的车辆。

2.2 下界

本文考虑作业可中断情形的最优解,并将其作为问题的下界。作业可中断,在本文研究的问题中可描述为1个订单上的产品可以分多次加工,每次只加工了一部分的产品,但是这部分产品是完成品,可以先行运送到客户手中用于交货,只是数量上不满足订单量,其中产品的加工时间与加工数量成正比。

在加工可中断的情形下,问题的最优解仍然满足本文的3个性质,由此提出可中断情形下的最优算法，具体如下：

(2) 将所有订单按照vjujlj/pj值从小到大排列,每个订单都均分成K个部分,分别由K辆车装载运送,即将所有订单的1/K订单量的产品全部加工完成后装车运送,重复加工运送K次,且每次订单都是按照vjujlj/pj值从小到大的顺序加工,具体如图3所示。

(3) 计算当前解的目标函数值,记为U′。若U′>U,则结束,返回U及其对应的集合Ki(i=1,2,…,K);若U′≤U,则令U=U′,K=K+1,返回到步骤(2)。

图3 可中断情形下的订单加工顺序

可中断情形最优算法是将每个订单平均分配给每辆车,每车的订单按照vjujlj/pj值从小到大的顺序加工。

定理1 可中断情形最优算法能够求得可中断情形下的最优解。

证明 假设定理不成立,即最优解不是按照可中断情形最优算法的规则排列的,根据性质2可知,若每一车辆上订单的加工顺序已经是最优的,则最优解会出现以下2种情形。

(1) 最优解的车辆数与可中断情形最优算法求得的车辆数相同,记为K。由性质2可知,订单排序既定,最优解与可中断情形最优算法求得解的不同之处在于每个订单的加工量不同,则最优解中至少存在某一个作业,有2辆车的加工量不等于该订单量的1/K。

图4 定理证明的分车加工顺序

现比较图4a与图4b所示方案变质成本的大小,令Δ1为图4a所示方案变质成本减去图4b所示方案变质成本，则有：

(7)

显然,由于x≠1,必有Δ1>0,即图4a所示方案的变质成本大于图4b所示方案的,这与图4a为最优解的假设相矛盾。

以上讨论的是2辆车的情形,接下来讨论多辆车的情形。设最优解中对于某一订单,有s辆车上的订单加工量都不等于该订单量的1/K,其中s≤K。

设Δ2表示最优解的变质成本减去可中断情形最优算法所得解的变质成本。在s辆车上订单Jj的加工量分别为ai,i=1,2,3,…,s,且a1+a2+a3+…+as=vj，则有：

(8)

由柯西不等式

可得：

(9)

(2) 最优解的车辆数与可中断情形最优算法求得的车辆数不相同,设最优解的车辆数为M,目标函数为U1;可中断情形最优算法求得车辆数为K,目标函数为U2;再令车辆数为M,运用可中断情形最优算法的规则求得该车辆数下的目标函数为U3。显然U2≤U3,根据情形(1)的证明可以得到U3≤U1,从而有U2≤U1,这与最优解的假设相矛盾。

以上2种情形下假设均不成立,故定理成立。

3 实验数据及分析

本文通过大量的实验数据将剩余容积最小车辆优先算法、订单加工时间和最小车辆优先算法与下界比较,验证2个算法的有效性。算法是运用Java语言编写,其开发平台为My Eclipse 8.5企业版;计算机的硬件配置为处理器Intel(R) Core(TM) i5-4590 CPU @ 3.30 GHz、内存4.00 GB;操作系统为Windows7 旗舰版。

实验中各个参数的范围如下:

(1) 订单数量n={20,40,60}。

(2) 车辆容积Q={50,100}。

(3) 车辆运送1次的固定成本F={20,50}。

(4) 订单的加工时间pj∈U[1,10],订单的体积vj∈U[10,20],订单产品的变质率uj∈U[0,0.01],订单产品的单位成本lj∈U[1,10]。

为了客观真实地反映2个算法的性能,本文针对Q、F、n的不同情形进行多次实验,每种情形下其他参数均随机产生且满足上述范围,每种情形下进行了5个不同算例的实验，结果见表1～表3所列。在3个表中,U0表示目标函数值的下界,K0为下界对应的车辆数;U1表示剩余容积最小车辆优先算法求得的目标函数值,K1为其对应的车辆数;U2表示订单加工时间和最小车辆优先算法求得的目标函数值,K2为其对应的车辆数;Gap1和Gap2分别表示剩余容积最小车辆优先算法和订单加工时间和最小车辆优先算法的误差界,其中,Gap1=(U1-U0)/U0,Gap2=(U2-U0)/U0。分析表1～表3中的数据可以得到以下结论：

(1) 在Q=50、F=20的情形下,剩余容积最小车辆优先算法的误差界在0.05～0.28之间不等,订单加工时间和最小车辆优先算法的误差界在0.03～0.14之间不等;在Q=100、F=20的情形下,剩余容积最小车辆优先算法的误差界在0.01～0.06之间不等,订单加工时间和最小车辆优先算法的误差界在0.01～0.04之间不等;在Q=100、F=50的情形下,剩余容积最小车辆优先算法的误差界在0.01～0.20之间不等,订单加工时间和最小车辆优先算法的误差界在0.01～0.21之间不等。

(2) 比较表1和表2可以看出,当其他参数相同、车辆容积较大时,剩余容积最小车辆优先算法与订单加工时间和最小车辆优先算法得到的解均更优。其原因是车辆容积大,能装载的订单数增多,节省了车辆的固定成本。

(3) 分析表2和表3可以看出,当其他参数相同、车辆固定成本较小时,剩余容积最小车辆优先算法和订单加工时间和最小车辆优先算法得到的解均更优。其原因是分析当车辆固定成本高时,为了降低车辆总成本,尽可能使用较少的车辆,每辆车均处于满载的状态,可能导致产品的变质成本增加,而车辆成本低,可以通过增加车辆来降低产品的变质成本。

(4) 从以上3种情况中可以看出,当Q较大F较小时,剩余容积最小车辆优先算法与订单加工时间和最小车辆优先算法求得的解更接近下界,解较其他2种情形更优。因此,剩余容积最小车辆优先算法与订单加工时间和最小车辆优先算法更适用于Q较大F较小的情形。

(5) 从总体上来看,订单加工时间和最小车辆优先算法的解比剩余容积最小车辆优先算法更接近下界,但是也存在例外的情况。可以通过结合2种算法的结果来确定方案。

表2 Q=100、F=20的实验结果

表3 Q=100、F=50的实验结果

4 结 论

本文研究了单机生产模式下多订单的生产及分车问题,即生产商按订单加工产品并装车运送到客户处。订单产品是具有易变质性的冷链产品,本文对产品的加工顺序及分车情况进行联合优化,优化的目标是使车辆成本与产品变质成本之和最小化。通过对问题的分析,本文提出了几条最优解的性质,在此基础上,提出了2个优化算法和1个问题下界,并通过实验数据将2个算法所得解与下界进行比较,结果表明，这2个算法能够求解出较优的联合调度与分车方案,并且在车辆容量较大、成本较小的情况下,算法的优化性能更好,能得到非常高质量的满意解。

[1] 杨爱峰,李佐平.基于产品变质和零售商部分延期支付的EOQ模型[J].合肥工业大学学报(自然科学版),2011,34(9):1413-1418.

[2] CHENG T C E,KAHIBACHER H G.Scheduling with delivery and earliness penalties[J].Asia Pacific Journal of Operational Research,1993,10(2):145-152.

[3] CHENG T C E,GORDON V S,KOVALYOV M Y.Single machine scheduling with batch delivery[J].European Journal of Operational Research,1996,94(2):227-283.

[4] MAZDEH M M,SHASHAANI S,ASHOURI A,et al.Single-machine batch scheduling minimizing weighted flow times and delivery costs[J].Applied Mathematical Modelling,2011,35(1):563-670.

[5] HAMIDINIA A,KHAKABIMAMAGHANI S,MAZDEH M M,et al.A genetic algorithm for minimizing total tardiness/earliness of weighted jobs in a batched delivery system[J].Computers & Industrial Engineering,2012,62(1):29-38.

[6] 倪志伟,朱旭辉,伍章俊.随机需求下多周期供应链库存配送联合优化模型[J].合肥工业大学学报(自然科学版),2015,38(1):121-126.

[7] AHMADIZAR F,FARHADI S.Single-machine batch delivery scheduling with job release dates,due windows and earliness,tardiness,holding and delivery costs[J].Computers & Operations Research,2015,53:194-205.

[8] ARMSTRONG R,GAO S,LEI L.A zero-inventory production and distribution problem with a fixed customer sequence[J].Annals of Operations Research,2008,159(1): 395-414.

[9] VIRGUTZ C,KNUST S.Integrated production and distribution scheduling with lifespan constraints[J].Annals of Operations Research,2014,213(1):293-318.

[10] AMORIM P,BELO-FILHO M A F,TOLEDO F M B,et al.Lot sizing versus batching in the production and distribution planning of perishable goods[J].International Journal of Production Economics,2013,146(1):208-218.

[11] 周泓,夏晓雯.易变质产品的生产计划与作业排序集成优化研究[J].计算机工程与应用,2010,46(18):192-195.

[12] CHEN H K,HSUEH C F,CHANG M S.Production scheduling and vehicle routing with time windows for perishable food products[J].Computers & Operations Research,2009,36(1):2311-2319.

[13] 李娜,王首彬.不确定需求下易腐产品的生产配送优化模型[J].计算机应用研究,2011,28(3):927-929.

(责任编辑 万伦来)

Integrated production and batch delivery scheduling for perishable products

MA Ying1,2, MA Jingjing1, LI Kai1,2

(1.School of Management, Hefei University of Technology, Hefei 230009, China; 2.Key Laboratory of Process Optimization and Intelligent Decision Making of Ministry of Education, Hefei University of Technology, Hefei 230009, China)

In this paper, the integration problem of production and batch delivery in cold chain environment under single-machine production mode is considered. Manufacturer produces the products of multiple orders on the single machine, then delivers them to customers by several identical vehicles. Extra deterioration cost is produced over time due to the perishability of products and vehicle cost is also produced from the delivery. So it is necessary to arrange production and delivery batches reasonably to minimize the total cost including vehicles cost and deterioration cost. Problem analysis is done firstly to present several properties of optimal solutions, based on which two algorithms and a lower bound are proposed. Finally, the validity of these two algorithms are shown by large-scale experiments of random data.

production; batch delivery; integrated scheduling; perishable product; single machine

2015-07-29；

2015-09-23

国家自然科学基金资助项目(71201046;71471052);安徽省自然科学基金资助项目(1208085QG133)

马 英(1979-),女,安徽淮北人,博士,合肥工业大学副教授,硕士生导师.

10.3969/j.issn.1003-5060.2017.01.023

O223;F406.2;TP301.6

A

1003-5060(2017)01-0128-08