圆柱形储液罐声发射检测的液体声速现场测量

方卫红

(后勤工程学院 后勤信息与军事物流工程系, 重庆 401311)

圆柱形储液罐声发射检测的液体声速现场测量

方卫红

(后勤工程学院 后勤信息与军事物流工程系, 重庆 401311)

提出了一种现场测量圆柱形储液罐液体声速的方法，并通过试验分析了影响测量精度的有关因素。液体声速测量采用常规的声发射检测布置方案，激发模拟声源产生振动，然后获取液体直达波的传播时间从而计算出声速。对比了断铅、30 kHz和60 kHz的三种模拟信号，结果表明高频成分为主的声源更有利于定位液体直达波。对阈值法、相关法和包络切线法三种波达时差计算方法进行了比较，结果表明包络切线法更有效。试验数据表明，提出的现场测速方法具有较高的精度。

液体声速;现场测量;声发射;脉冲;波达时差

在对储液罐底板进行声发射检测时，底板声源和罐壁传感器之间声波传播的介质主要是罐内液体，声发射评估系统需要利用液体声速来确定声源位置，故液体声速是否准确将影响到评价结果的准确性。常温常压条件下的声发射检测工程实践中，大多使用固定的或者通过经验获得的声速值[1]，某些缔合液体如水，还可以计算不同压力、温度下的声速，从而获得更为精确的声速值[2]。对于特殊环境条件或者Kneser混合液体，如石化产品而言，则需要通过试验方法才能获得符合要求的声速。液体声速用变形模量和介质密度表示[3]，但是变形模量难以获得，测量液体声速通常采用其他方法，如驻波法[4-5]、光栅法[6]、兰姆波法[7]和脉冲时差法[8-12]等。试验方法精确可控，通过批量试验可以获得不同环境条件下的声速，是声速测定标准的推荐方法，在科学研究中应用较多。但是试验方法需要特殊的测量装置，对被测液体采样，并模拟与储罐一致的储存条件，这些增加了声发射检测工程的工作量，在进行批量储罐声发射检测时比较费事。在被检储罐上直接测量液体声速可以避免这一问题，但是由于声波信号在储罐内的传播模式比较复杂，目前鲜有这种方法的应用探讨。为此，笔者采用声发射检测工程的常用配置，提出了一种基于脉冲时差法的现场测速方法，这种方法的测量精度与模拟声源、波达时间计算方法有关，并通过试验对此进行了研究。

1 测量原理

声发射检测系统按储液罐底板声发射检测工程的要求进行布置，如图1所示，多个声发射传感器均匀安装在离罐底一定高度h的罐壁圆周上，罐内液位H远高于传感器安装高度。测速所需的声波在罐壁传感器附近位置激发，模拟声源为短时脉冲信号。

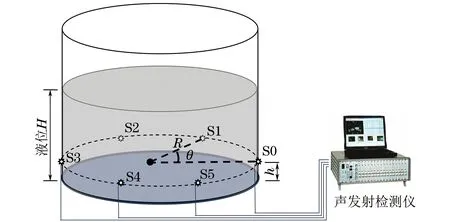
图1 声发射检测系统布置示意

脉冲时差法利用脉冲声波在液体中的传播距离和时间来计算液体声速。用二维极坐标来标识模拟声源和传感器所在平面，储罐半径为R，位于(R,0)极坐标位置的模拟声源在罐壁上激发出振动后，声波通过储罐壁板和液体等介质的不同传播路径到达位于(R,θ)极坐标位置的传感器。一般情况下，纵波、弯曲波和液体直达波是传感器最早接收到的三个信号，其他反射声波随后到达。以t1表示纵波沿罐壁传播到达传感器的时间，t2表示弯曲波沿罐壁传播到达传感器的时间，t3表示通过液体介质直线传播到达传感器的时间，则液体声速CL可表示为：

式中的R,θ都是测速前可确定的，只要计算出t3，便可以获得液体声速。

计算t3之前，先要从传感器信号中分离出液体直达波成分。对于金属材料储罐而言，通过壁板传播的纵波波速远高于弯曲波及液体直达波波速，比较容易排除。而沿壁板传播的弯曲波是频散的，传播速度和频率有关。如果弯曲波的频率成分比较复杂，那么其有可能和液体直达波混合在一起到达传感器，对测速会造成较大影响。因此，这种现场测速方法需要控制模拟声源的频率成分，笔者通过对三种不同频率成分脉冲声源的试验，探讨了模拟声源的选择依据。

t3可用两个传感器信号的波达时差来表示，即靠近声源的传感器采集信号x0和远端传感器检测到的液体直达波信号x1之间的波达时差。x0和x1都是短脉冲信号，其波达时差计算方法较多，最常用的是阈值法和互相关法[13-15]。阈值法将信号幅值首次越过指定阈值的时间作为波达时间，传播时间为x1和x0两个信号波达时间的差值。阈值法抗噪性能差，对阈值敏感，相比之下高幅值脉冲x0波达时间的计算误差较小，而缓升型信号x1则会出现较大计算误差。互相关法计算x1,x0的相关序列时，根据序列最大值位置确定时差。互相关法抗噪性能更好，但是对信号之间的相关度有依赖性。声源近端的x0信号主要由纵波和弯曲波混和而成，而远端的x1信号则是以液体直达波为主，它们之间的相关程度不高。此类信号，应用更为复杂的时频分析方法[16-17]也难有好效果。为此，笔者提出了一种包络切线法来计算波达时间。如图2所示，包络切线法首先构造信号的幅值包络线，在包络线越过阈值的起点位置以包络线斜率构造一直线(包络切线)，该直线与信号均值水平线的相交位置被确定为波达位置。三种波达时差计算方法的优劣通过后续试验数据分析可以得到。

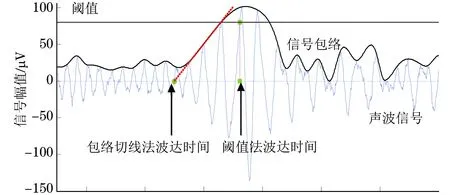
图2 包络切线法和阈值法示意

2 试验方法

试验用碳钢材料的储罐直径9 m，壁厚5 mm，所储液体为水，液位3.15 m。声发射检测系统为VALLEN的ASYS-5型仪器，在离罐底高0.2 m的罐壁圆周上平均分布6个声发射传感器VS30用于检测信号，其频率范围为25 kHz～80 kHz。

试验使用的模拟声源有三种。一是断铅，另外两种30 kHz和60 kHz的脉冲信号来自信号发生器PAC FieldCAL。信号发生器也连接一个VS30传感器，该传感器专用于激发振动声波，紧贴其他检测传感器安装。

试验中采用全波形方式记录信号，采样频率2 MHz。在每个检测传感器附近位置依次激发三种模拟声波，每个位置每种模拟声波各激发20次，两次模拟声波的间隔时间在2 s以上。

试验期间，天气多云微风，经测量罐内水温为(16.8±0.2) ℃。

3 试验数据分析

试验中碳钢板的物理参数为：密度ρ为7 800 kg·m-3，杨氏模量E为2×1011Pa，泊松比σ为0.28。常压状态下，16.8 ℃的水中声速CL为1 472 m·s-1，其依据的声速计算公式为(其中T为温度，℃)[2]：

CL=1 402.336+5.033 58T-

由于传感器均匀分布在圆周面上，故距离声源相同距离的传感器接收到的声波信号是一致的，试验数据也证明了这一点。为了描述方便，后续试验分析的声源位置都假设在S0附近。

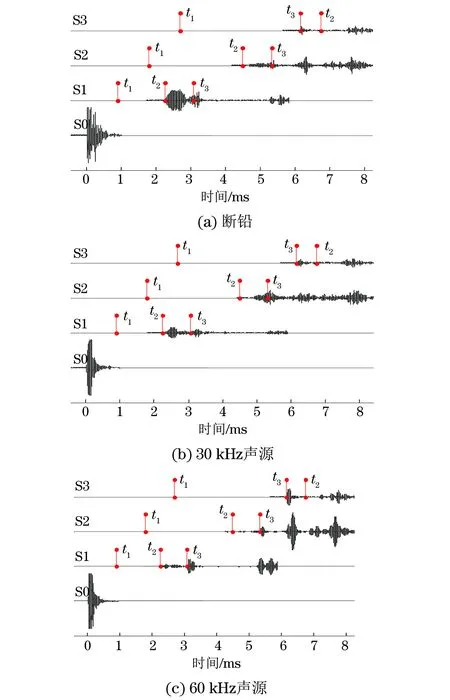
图3 三种声源激发后四个不同位置传感器接收到的信号

3.1 声波传播过程

在S0附近激发模拟声波后，S0,S1,S2和S3四个传感器接收到的声波信号如图3所示。为了提升信号的显著程度，图中波形幅值做过处理，同一传感器的幅值缩放比例是一样的，但不同传感器的幅值缩放比例不一样。观察全波形信号， S1、S2和S3三个位置t1时间都未接收到显著的纵波，表明三种模拟声源都未能产生足够强的纵波，因此纵波可以忽略不计。

t2时间(以传感器高限频率80kHz计算)之后到达的弯曲波是频散的，其频率越低的成分传播越慢。传感器接收到弯曲波的时间为：

式中：Cp为弯曲波传播速度;d为碳钢板厚度;f为信号频率。

若液体直达波未能先于频率最高的弯曲波成分到达传感器，则弯曲波的低频部分将和液体直达波产生混合。在弯曲波先到的S1和S2位置，检测信号中可以明显发现这种混合现象。

另一方面，由于罐内液体的作用，沿罐壁传播的弯曲波高频部分信号更容易泄露进入液体。根据SNELL折射定律，弯曲波沿罐壁传输相当于以90°角入射壁液交界面，传播速度高于液体声速的弯曲波成分会折射进入液体，而传播速度低于液体声速CL的弯曲波成分则不会进入液体。临界频率fc为：

在文章的试验条件下，fc约为34kHz，高于34kHz的弯曲波信号难以在板中远距离传输。图4(图中各分图纵坐标以各信号的最高值为基准进行了归一化处理)表明S0位置检测的断铅和30kHz两种模拟声源的信号中都有低于fc的较强的弯曲波成分，所以这两种信号传播到S2位置时弯曲波依然显著。而60kHz模拟声源信号中主要频率成分都高于这一临界频率，信号传播到S2位置时弯曲波基本消失。S3位置首达波为液体直达波，直达波信号中高于临界频率的成分较多，而低于临界频率的成分较少。

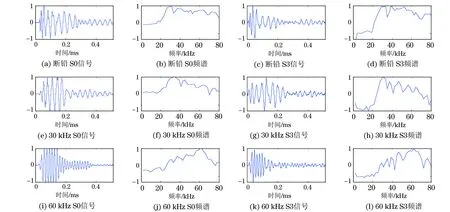
图4 三种声源传播到S0和S3位置的信号波形与频谱特征

因此，如果模拟声源激发出以高于临界频率成分为主的振动信号，在距离声源较远的位置检测就可以消除弯曲波的影响。

3.2 声速测量误差

S3和S2位置传感器检测到的信号都可用来计算液体直达波传播时间，从而测量出声速。在S3和S2两个位置,对三种模拟声源采用三种不同波达时间计算方法测量的声速误差直方图见图5，6。

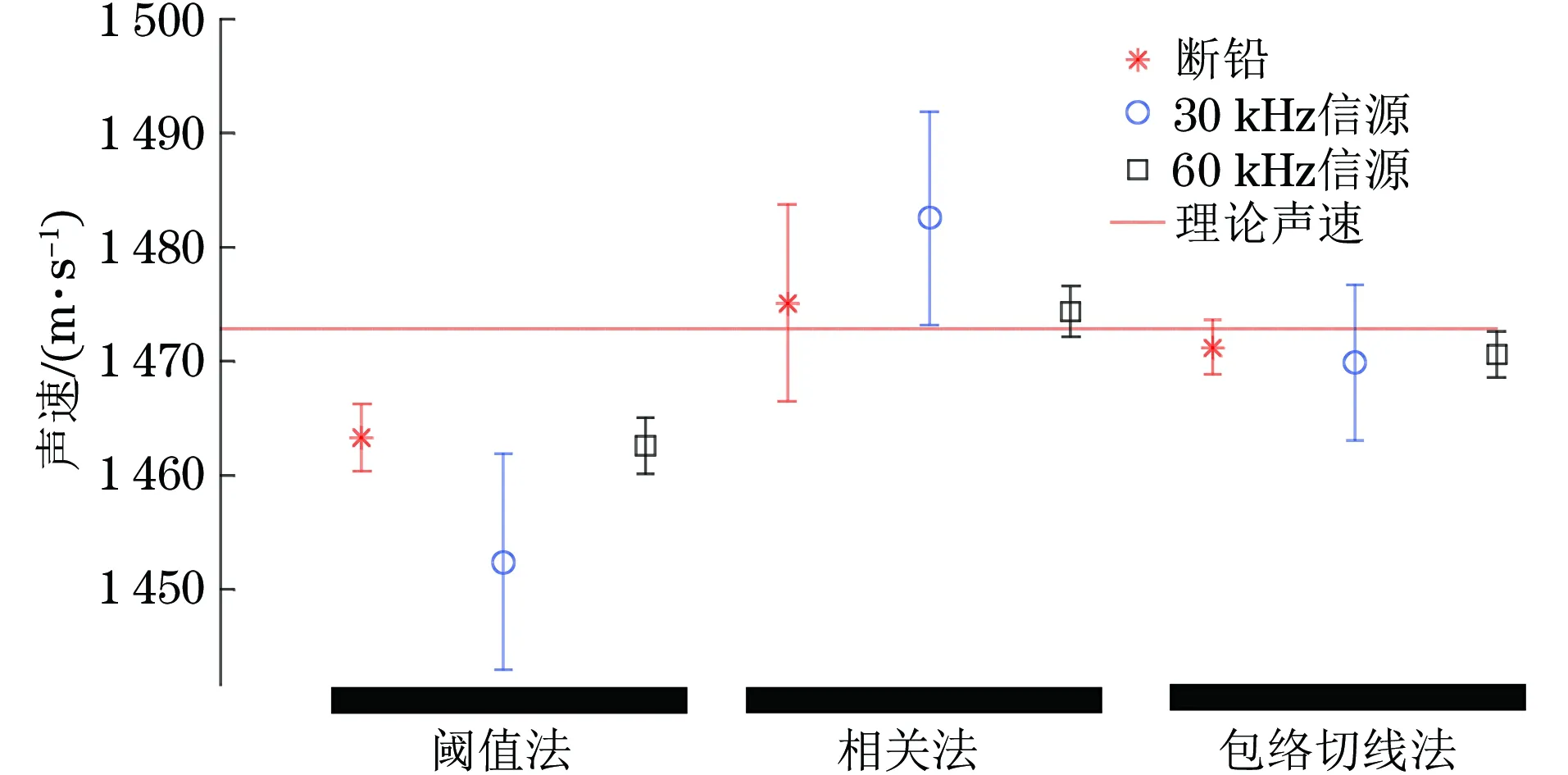
图5 S3位置计算声速的误差直方图

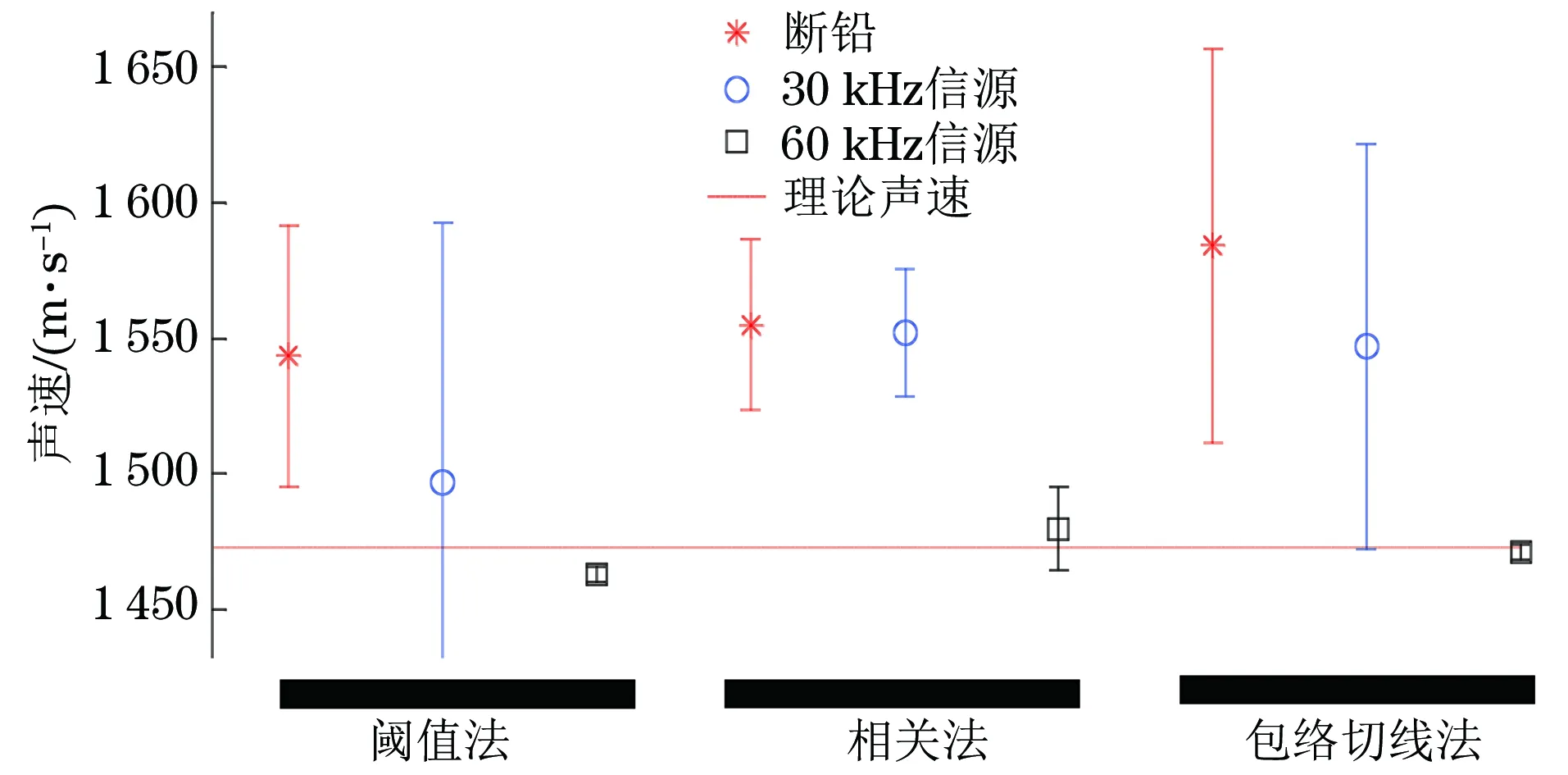
图6 S2位置计算声速的误差直方图

S3位置检测到的首波为液体直达波。由于试验液体介质为水，S3位置的弯曲波在液体直达波之后到达，没有对液体直达波形成干扰，此时各类声速测量方法的误差都较小。石化产品的声速低于水中声速，大多数储油罐不会出现弯曲波先于液体直达波到达的情况，因此S2位置的声速计算更有意义。60 kHz模拟声源信号传播到S2位置时弯曲波成分基本消失，此时S2位置接收的首波信号是液体直达波，因此声速测量误差较小。断铅和30 kHz模拟声源的低频信号丰富，在S2处检测到的首波信号还是弯曲波信号，以首波信号来推算声速，可以发现测量值明显高于理论值。

从模拟声源类别来看，60 kHz模拟声源的测量效果最佳，30 kHz模拟声源所测声速的方差最大，而断铅信号频率成分丰富，效果居中。

从三种波达时差计算方法的效果来看，阈值法的测量误差波动也小，但是所测声速偏低。总体来看包络切线法最佳，测量均值更接近理论值，误差波动也更小。

采用60 kHz模拟声源和包络切线法时，在S2位置检测信号测得的声速为(1 471.1±2.9) m·s-1，在S3位置检测信号测得的声速为(1 470.5±2.0) m·s-1。

4 结论

(1) 提出的利用储罐底板声发射检测常用的布置方式，在罐壁上激发声源，检测信号并测速的方法可以获得误差较小的液体声速。

(2) 模拟脉冲信号的主要频率成分应高于临界频率。

(3) 选择更远端的传感器参与测速，这些传感器位置检测到的首信号是液体直达波。

(4) 提出的包络切线法比阈值法、相关法计算的波达时差更准确，更有利于获得准确的声速。

[1] 陈健飞,仇东泉,盛华,等. 常压储罐底板声发射检测自标定的影响因素[J].无损检测，2012,34(12):81-84.

[2] 马大猷, 沈壕. 声学手册[M]. 北京：科学出版社，2004.

[3] 何琳, 朱海潮, 邱小军. 声学理论与工程应用[M]. 北京：科学出版社，2006.

[4] 李荣福, 高春歌, 李宪龙. 测量液体声速的几种方法的探讨[J].大学物理实验, 2002, 15(4):1-3.

[5] 张颖, 王升, 郑雄. 利用自发布里渊散射测量液体声速[J].物理学报, 2015(3): 452-458.

[6] 吴庚柱, 王建华. 超声光栅测液体声速原理和实验[J].大学物理实验, 1999 (4):6-10,75.

[7] 陈智军，李良儿，施文康，等. 一种测量液体声速的兰姆波传感器[J]. 上海交通大学学报,2008，42(2):290-294.

[8] 伍肆, 冯晓娟, 林鸿. 差分飞行时间法精密测量高压液体声速的研究[J].计量学报,2015,36(4):337-343.

[9] 韩学辉, 李峰弼. 一种免刻度的高温高压液体声速透射测量方法及装置[J].中国石油大学学报(自然科学版), 2015, 39(3): 57-61.

[10] BALL S J, GOODWIN A R H, MARTIN TRUSLER J P. Phase behavior and physical properties of petroleum reservoir fluids from acoustic measurements[J].Journal of Petroleum Science and Engineering, 2002, 34 :1-11.

[11] AZEVEDO R D, JSZYDLOWSKI,PFPIRES. A novel non-intrusive microcell for sound-speed measurementsin liquids[J].J. Chem. Thermodynamics,2004, 36: 211-222.

[12] HDASHTI H,MRRIAZI. Acoustic velocities in petroleum fluids: measurement and prediction[J].Journal of Petroleum Science and Engineering, 2014, 124:94-104.

[13] 刘卫东, 张薇, 窦林名. 声发射定位中时差计算研究[J]. 计算机工程与科学, 2009,31(4)：127-129.

[14] ZIOLA S M, GORMAN M R. Source location in thin plates using cross-correlation[J].J. Acoust. Soc. Am., 1991,90: 2551-2556.

[15] 吴旭景,杜斌,叶陈. 基于EMD和小波分解的管道泄漏声发射源定位[J].无损检测,2015,37(10):60-63.

[16] SUZUKI H, KINJO T, HAYASHI Y, et al. Wavelet Transform of Acoustic Emission Signals[J].Journal of Acoustic Emission, 1996,14:69-84.

[17] 杨建波, 王阳,高虹. 小波变换用于声发射波波达时间的研究[J]. 无损检测,2001,23(11):482-484.

In Situ Measurement of Sound Speed in Liquid for Acoustic Emission Testing of Cylindrical Liquid Storage Tank

FANG Wei-hong

(Department of Logistical Information and Military Logistics, Logistic Engineering University, Chongqing 401311, China)

An in situ measurement method of sound speed in liquid for acoustic emission testing of cylindrical storage tank was proposed, and some factors influencing the precision were also analyzed by an experiment. The approach was based on the normal acoustic emission testing scheme, and a simulation source was used to stimulate vibrations which could be detected by some sensors, finally the sound speed was conducted by computing the transportation time of the first wave directly arriving at through liquid. In the following experiment, three simulation signals, namely break pencil, 30 kHz and 60 kHz,were compared to find that the pulse of high frequency is the best choice on locating the first wave directly arriving at through liquid.The experiment revealed that the envelop-tangent method was superior to the other two methods (the threshold method and the cross-correlation method) in computing the time difference of arrival waves. The study also showed that the accuracy of this in situ measurement method was very high.

Sound speed in liquid; In situ measurement; Acoustic emission; Pulse; TDOA

2016-05-22

方卫红(1972-)，男，硕士，副教授，主要从事检测技术及自动化装置研究工作。

方卫红，E-mail: fweih@163.com。

10.11973/wsjc201702013

TG115.28;TH824

A

1000-6656(2017)02-0052-05