基于高阶加权和迷宫算法的层析成像射线追踪法
黄晓寒,王仲刚,袁 野,张 彧
(后勤工程学院 军事土木工程系,重庆 401311)
基于高阶加权和迷宫算法的层析成像射线追踪法
黄晓寒,王仲刚,袁 野,张 彧
(后勤工程学院 军事土木工程系,重庆 401311)
通过对LTI线性插值法的追踪公式和全局扫描方法的改进,提出了一种基于高阶加权和迷宫算法的层析成像射线追踪法(HLTI)。该算法通过引入Taylor加权高阶项对LTI追踪公式进行改进,减小了由于线性条件假设而产生的累积误差,提高了射线追踪精度,解决了LTI追踪公式出现复值解而失效的问题;并利用迷宫算法原理对全局扫描方式进行优化,解决了传统扫描方法不能反向和竖向追踪的问题。仿真试验结果表明,新算法HLTI较传统的LTI算法具有更高的射线追踪精度和更好的成像效果。
LTI线性插值法;泰勒展式;CT技术;扫描优化
线性插值射线追踪[1-2]又称LTI(Linear Travel-time Interpolation),于1993年作为地震CT的正演过程被提出,主要用于地质勘探、震源的排查。作为全局算法的一种,LTI由追踪公式和扫描方法两部分构成。
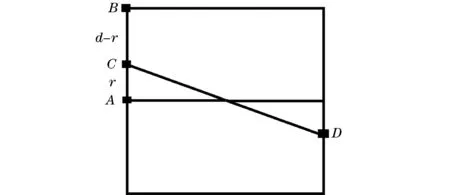
图1 计算D点的走时TD
追踪公式推导如下。图1为一离散网格,网格内的慢度S是恒定的,点A,B,C和D坐标分别为(x1,y1),(x1,y1+d),(x1,y1+r)和(x2,y2)。A,B点的走时为TA和TB,射线穿过网格边界AB线段上的C点(x1,y1+r)到达对面边界D点(x2,y2)的走时TD可表示为:
(1)
由线性假设可得:
式中:d为AB间的距离;r为AC间的距离。
将式(1)代入式(2)可得:
根据Fermat原理,将式(3)对r求导,令dTD/dr=0,得到TD取最小值时的r值:
式中:ΔT=TA-TB,Δx=x2-x1,Δy=y2-y1。
将r代入式(3),可求得TD的最小值:
C点在AB线段上可得到约束条件:
全局扫描分为向前处理和向后处理两部分,皆采取按列的扫描方式。通过式(5)可计算出起点到接收点之间各像元边界点上的走时,称为线性插值追踪的向前处理;通过式(4)可以准确定位最小走时所对应的像元边界交点,称之为线性插值追踪的向后处理。
1 LTI算法误差分析
LTI法追踪公式的核心在于线性假设式(2),基于理论方面的LTI算法误差分析如下。
如图1所示,网格内慢度为S。射线从激发点发出经由C点到达D点,从激发点到C点所经历的慢度为S。则C点及其邻近两点A、B处的旅行时间可以表示为:
将TB和TC在A点Taylor展开得:
将式(10)和式(11)相减,整理即得:
分析式(12)可知:① 当单元网格边界插值点的数量趋近于正无穷时,式(12)中的r→0、d→0,此时该式即为传统的LTI算法式(2)。② 作Taylor展开所得的高阶系数与A点走时TA成反比关系,又由于A点时间和激发点到A点的距离成正比关系,故点C距离激发点越远,高次项的影响越小。反之,当C点越接近激发点,带来的误差越大。LTI算法于1993年作为地震CT的正演过程被提出,主要用于地质勘探、震源的排查。在这类检测中,精度不高,且激发点和接收点距离较远,使得高阶系数的影响不大。但由于工程检测[3]中受测断面小,激发点和接收点距离近,高阶项的误差就不可忽略,因此传统LTI算法在工程CT中的应用将会受到限制。
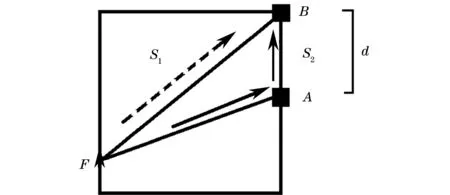
图2 路径公式出现复数解
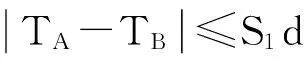
为了解决以上两个问题,笔者将根据工程CT特点,从追踪公式和扫描算法两方面对传统LTI算法进行改进,并提出了一种基于高阶加权和迷宫算法的层析成像射线追踪法(HLTI)。
2 HLTI算法追踪公式推导
基于上述分析,对传统的LTI追踪公式进行了改进,通过引入Taylor高阶项来修正传统LTI的线性假设所带来的误差,不但提高了追踪精度,而且避免了追踪公式在全局扫描过程中因出现复数解而失效的问题。下面介绍改进后的追踪公式及其稳定条件的推导。
将TC在r=0处Taylor展开,根据展式正负交替出现的性质,对其三阶及以上的高阶项放缩,并把放缩以后的项作为权值与二阶项合并,得:
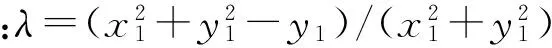
根据图1所示,TD为D点的旅行时间,有表达式:
为了与TC形式上统一,对TD第二项做Taylor展开,保留二阶项得:
代入式(13)则可得TD的最终表达式:
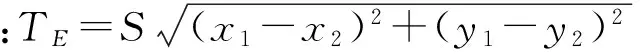
根据Fermat原理,对式(16)作r的变分即得:
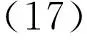

-2dQ2≤Q1≤0(r的稳定条件)
式中:
3 HLTI算法全局扫描方法
对于射线追踪技术来说,扫描方式与追踪公式同等重要,传统LTI法的扫描方式存在的问题有:扫描采用从左往右按列的扫描方式,人为限定了搜索顺序,无法进行反向和纵向追踪;编程步骤冗长繁复,存在大量重复运算。为了解决这些问题,笔者基于迷宫问题[4]中路径寻优的思想,提出了一种新的扫描方法。新方法包括定义数据结构和数据传递方式两部分。
(1) 定义数据结构。检测断面划分为一系列小网格,每个网格看作独立的数据结构,每个数据结构所含数据为该格慢度S,8个点对应走时t1,t2,t3,t4,t5,t6,t7,t8和对应坐标量(x1,y1),(x2,y2),(x3,y3),(x4,y4),(x5,y5),(x6,y6),(x7,y7),(x8,y8),如图3所示。
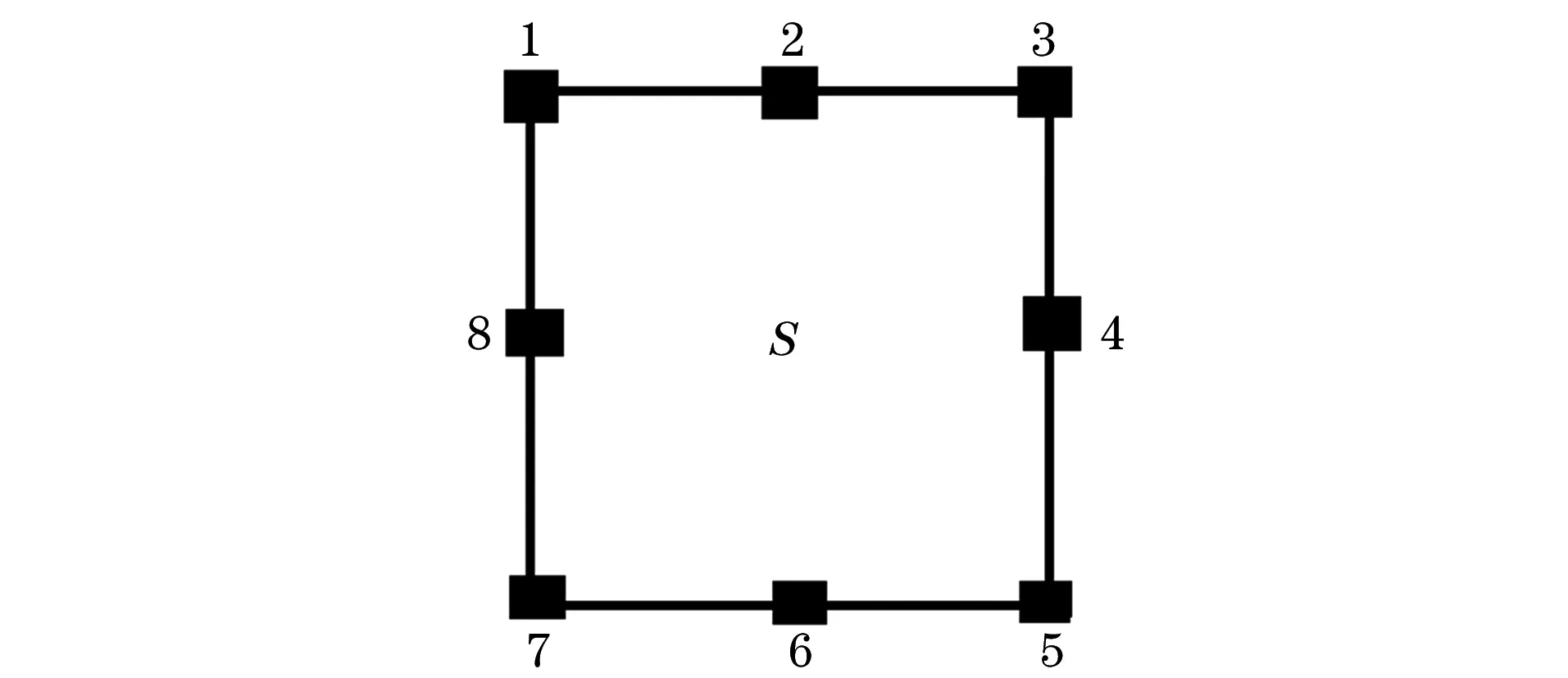
图3 单个数据结构示意
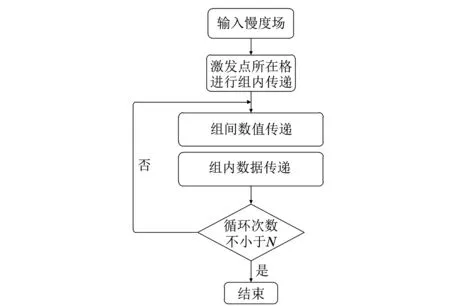
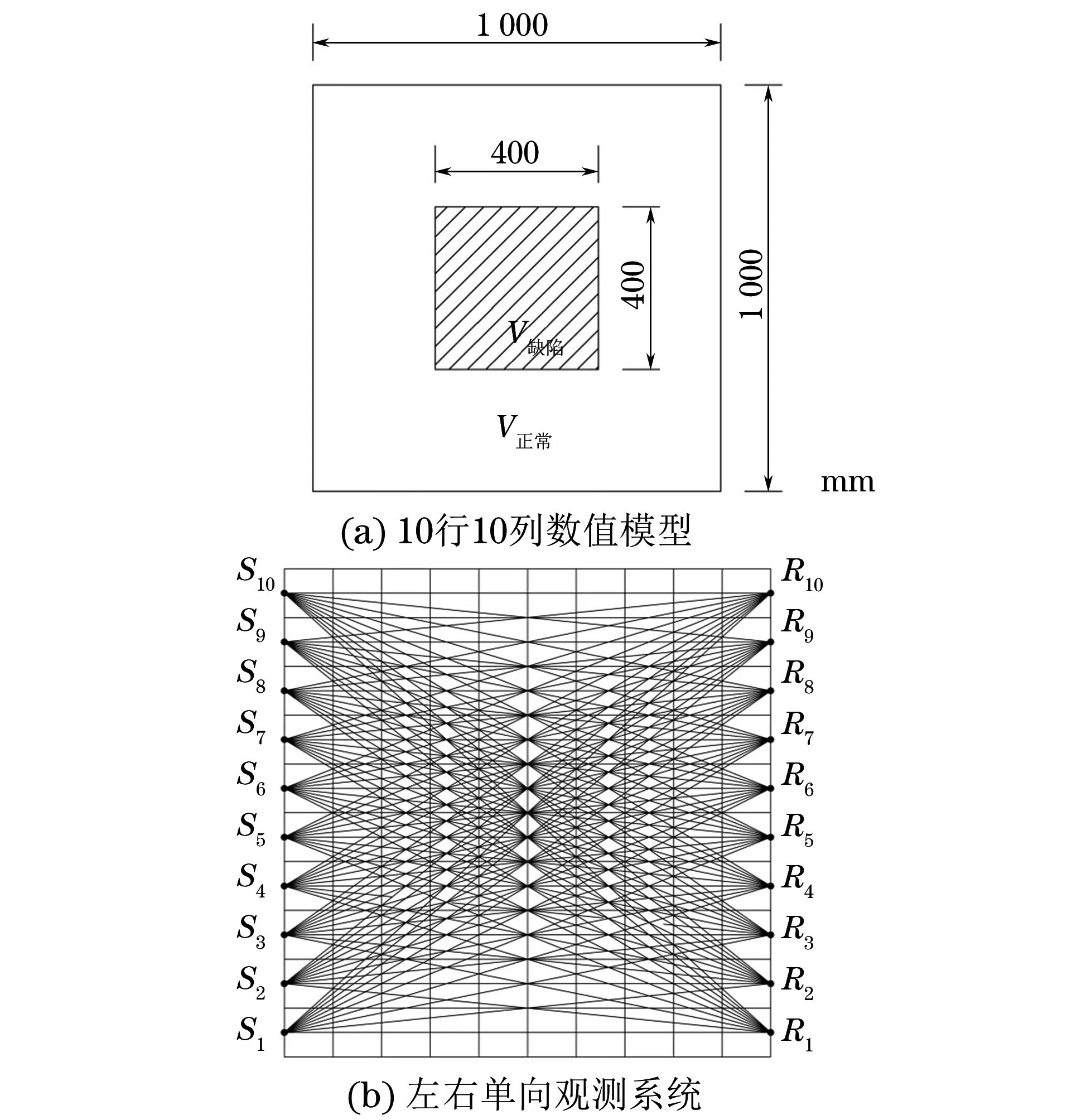
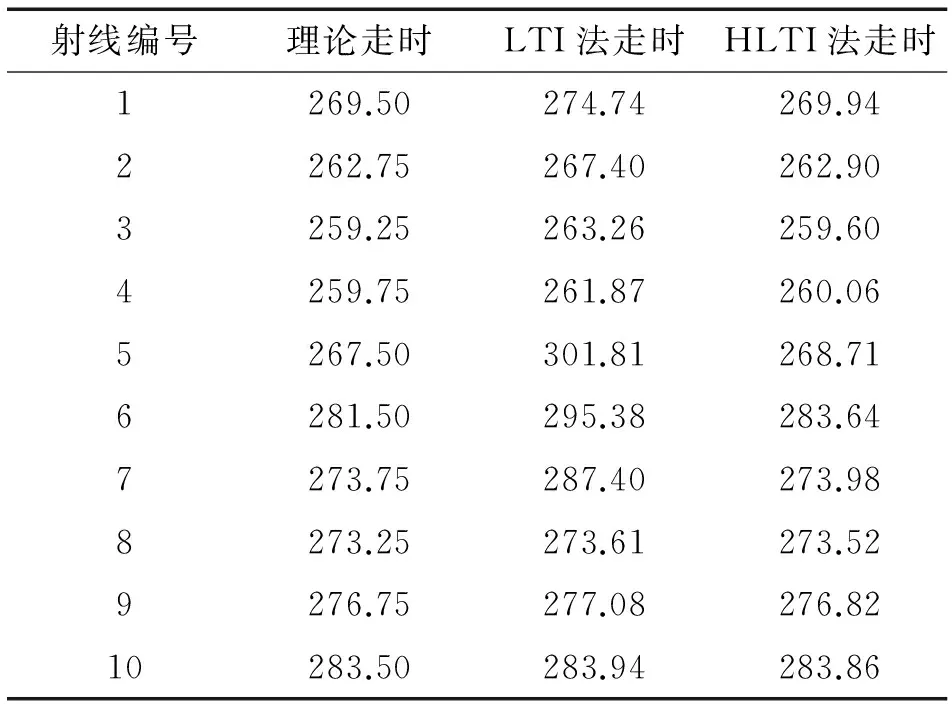
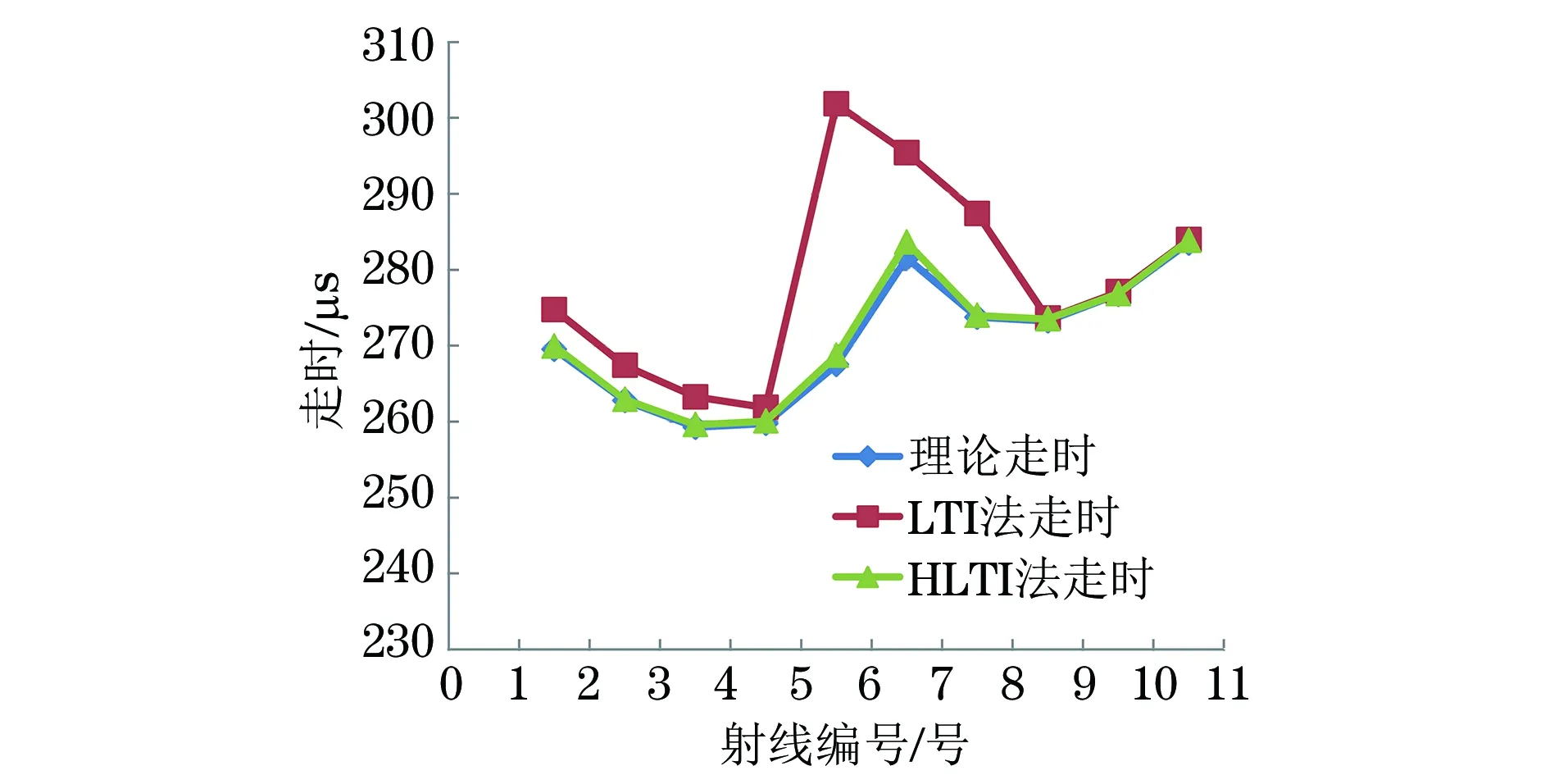
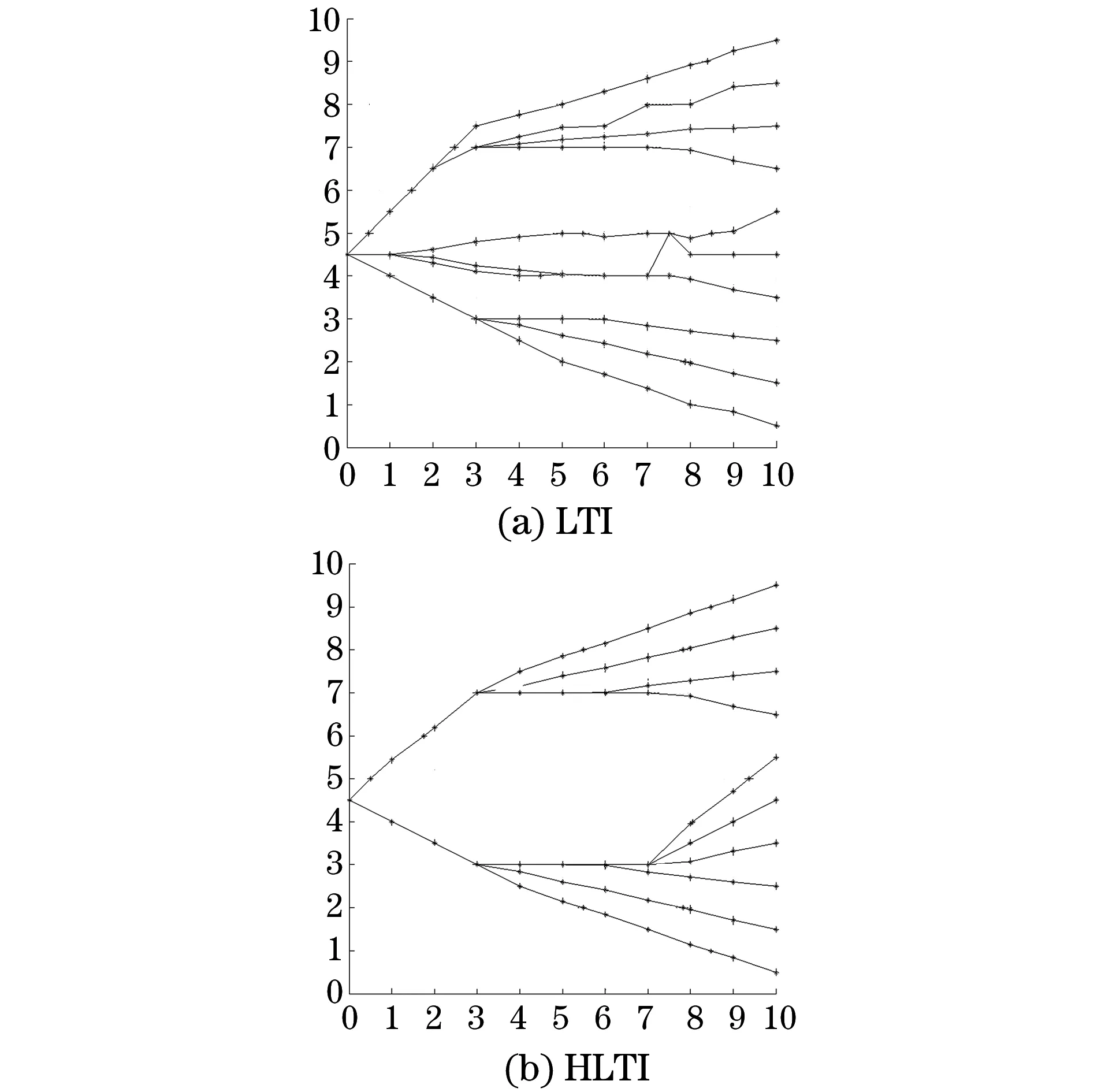
(2) 定义数据传递方式。如图4所示,对数据组中第4个点赋值走时的方法有两种。一种如图中虚线所示,通过数据组内已知的走时和坐标数据,以追踪公式(17)、(18)计算求得,并将其中最小值赋给第4个点,称这种数据传递方式为组内数据传递。另一种如图中实线所示,网格A和B相邻,A中第4个点与B中第8个点重合,对应点的走时、坐标应相同。若8 图4 数据传递方式示意 综上,HLTI算法流程如图5所示。 图5 HLTI算法流程 图6 数值模型与观测系统 设计一个如图6(a)所示的含缺陷的数值化模型,截面长1 000 mm,宽1 000 mm,波速为ν正常=4 000 m·s-1,缺陷区域波速为ν缺陷=3 000 m·s-1。设置激发点10个,接受点10个,采取一发多收信号采集方式,网格100个,射线100条,收发点布置方式和初始射线路径见图6(b),不失一般性,以第5号激发点及其对应的10条射线为例进行分析。 表1 LTI和HLTI走时对比与相对误差 μs 图7 理论走时和两种算法的离差曲线 通过射线走时和射线路径与理论值的对比分析,判定两种算法的追踪效果。表1为10条射线的理论走时与通过两种射线追踪方法得到的走时值和误差计算,图7为两种方法走时与理论值的离差曲线。图8为两种算法追踪出的射线路径。由表1可知, LTI算法和HLTI算法与理论走时的最高误差分别为12%和0.7%,平均误差分别为2.9%和0.2%,HLTI算法的最大离差不超过2.1 μs,小于LTI算法,走时曲线与理想走时曲线更为贴近,提高了追踪精度。在图8(a)中的第4、5、6根射线无法绕开缺陷,而8(b)中通过向上搜索基本绕开了缺陷区。故通过分析可得出结论:在含低速区的慢度场中,HLTI算法能解决LTI算法无法纵向追踪的问题,具有更好的射线追踪效果。 图8 两种算法的射线追踪路径 通过对LTI线性插值法的追踪公式和全局扫描方法的改进,提出了一种基于高阶加权和迷宫算法的层析成像射线追踪法(HLTI)。新算法通过引入Taylor高阶项减少了原算法追踪公式的误差,避免了原有追踪公式出现复数解导致追踪失效的情况;对其全局扫描方法进行改进,解决了原方法无法纵向追踪的问题。算例验证表明,提出的HLTI算法较传统的LTI算法具有更高的射线追踪精度,获得了更好的追踪效果。 [1] VIDALE J E. Finite-difference calculation of travel times[J]. Geophysics, 1988, 78: 2062-2076. [2] 李强, 白超英. 复杂介质中地震波前及射线追踪综述[J].地球物理学进展,2012,27(1): 92-104. [3] 顾孝同. 国内工程CT技术的发展与应用[J]. 工程地球物理学报, 2006,3(4): 278-282. [4] 吴建明. 电脑鼠走迷宫算法模拟器的仿真建模与实现[J].电脑开发与应用,2014, 27(2): 33-39. Tomography Ray-tracing Based on High-order Weighting and Maze Algorithm HUANG Xiao-han, WANG Zhong-gang, YUAN Ye, ZHANG Yu (Department of Civil Engineering, Logistic Engineering University, Chongqing 401311, China) Through the improvement to the LTI track formula (linear travel-time interpolation) and global scanning method, a HLTI based on higher order weighting and maze algorithm has been advanced. By means of improving LTI track formula via bringing in Taylor higher order weighted item, this new algorithm reduces the accumulative error caused by linear condition hypothesis, improves the accuracy of ray-tracing, and thus solves the invalidation problem come about by the complex-value solution of LTI track formula. Besides, by taking advantage of the maze algorithm principle to optimize the global scanning method, the problem of the traditional scanning method which is incapable of backward and vertical tracing has been solved. The simulation experiment results indicate that the new HLTI has higher ray-tracing accuracy and better image quality than the traditional LTI. Linear travel-time interpolation; Taylor expansion; CT Technique; Scan optimization 2016-05-25 黄晓寒(1990-),女,硕士,讲师,主要研究方向为特种结构检测与加固。 黄晓寒,E-mail:hxhshr@sina.com。 10.11973/wsjc201702009 TG115.28 A 1000-6656(2017)02-0034-04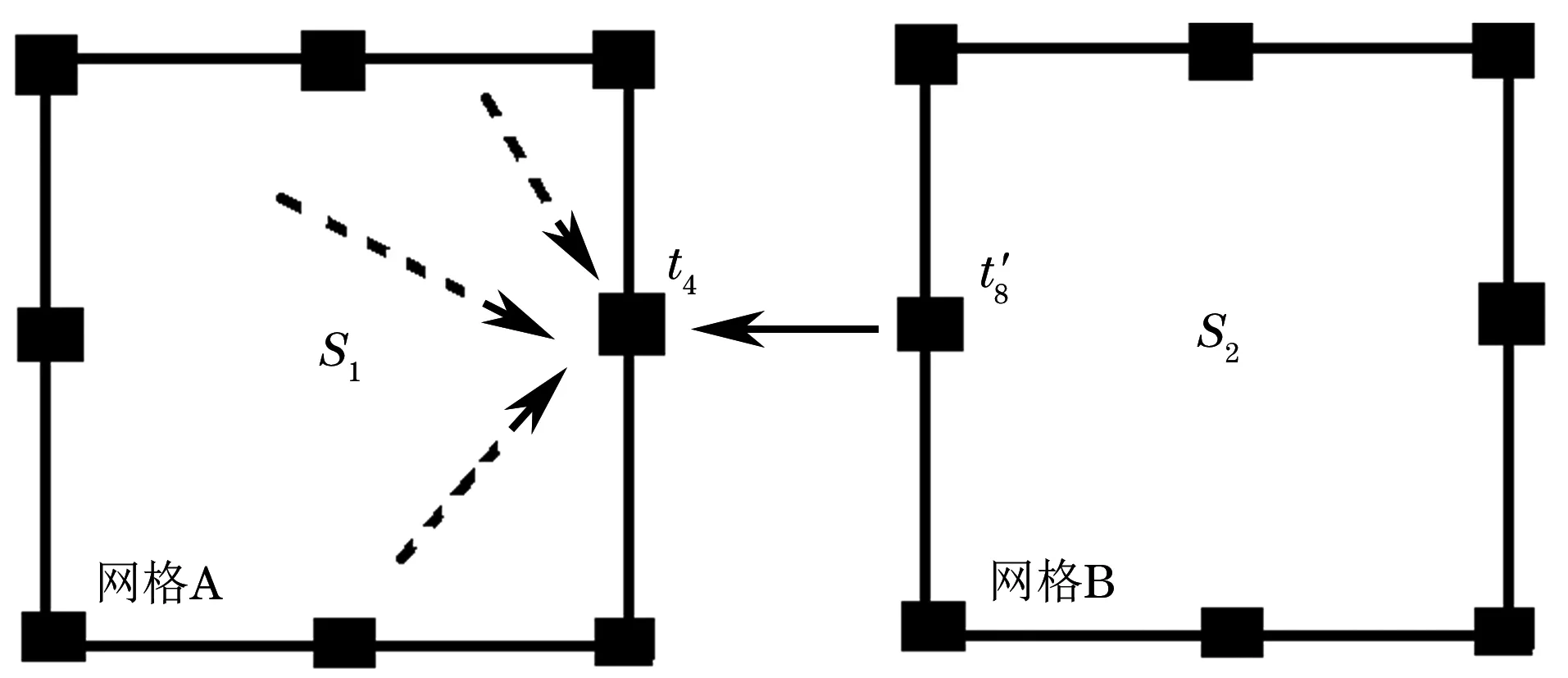
4 仿真试验
5 结语

