复合材料多钉连接孔周应力场的数值模拟方法研究

姚 烨 金 浩 陈夏良 赵应江 严仁军

(高性能船舶技术教育部重点实验室1) 武汉 430063) (武汉理工大学交通学院2) 武汉 430063) (湖北省麻城市公路管理局3) 麻城 438300)

复合材料多钉连接孔周应力场的数值模拟方法研究

姚 烨1,2)金 浩3)陈夏良2)赵应江1,2)严仁军1,2)

(高性能船舶技术教育部重点实验室1)武汉 430063) (武汉理工大学交通学院2)武汉 430063) (湖北省麻城市公路管理局3)麻城 438300)

通过模拟复合材料多钉连接试验，采用ABAQUS建立有限元模型，提出3种计算复合材料多钉连接孔周应力场的数值模拟方法.结果表明，简化接触法与实验值的误差较大，插补法和准静态分析法与实验值的误差相对较小并得出复合材料多钉连接孔周应力分布情况.

复合材料；多钉连接；应力场分析；数值模拟

0 引 言

复合材料由于比强度高、比模量高、耐腐蚀等优异性能，在舰船结构中获得广泛应用.近年来，随着复合材料设计、制造的发展，成为未来舰船结构设计的重要发展方向[1].复合材料与其他部件连接是不可避免的，机械连接连接强度高、便于装卸，安全可靠，其中螺栓连接最为常见，含孔层合板会产生局部应力集中现象，应力集中的产生会削弱接头的结构强度[2-3]，对复合材料螺栓连接孔周应力场进行研究是十分有必要的.

在螺栓连接的复合材料结构分析中，所使用的有限元模型一般都是单钉接头[4-8]，原因是每增加一个螺栓，就增加了数个接触对，计算的非线性和复杂性明显增加，很多时候都无法获得收敛解.对于复合材料多钉连接孔周应力分布问题，很多学者从理论上进行求解，Kradinov等[9]在平面弹性力学的基础上用变分原理得到了控制方程，计算得到了多种不同机械连接件的应力分布；苏杰等[10]利用Faber工具转变成解析函数边值问题，得到了应力函数.在数值计算方面，通常的做法是简化接触关系，将接触的2个面绑定(Tie)或将多个接触体建成一个整体，这种方法虽然对远离接头区域的影响较小，但不能准确的反映出接头周围的孔周应力变化，文中针对复合材料多钉连接问题，提出了3种可能解决的办法.

1 计算模型

文中采用ABAQUS模拟了文献[11]中的实验，复合材料夹芯板为600 mm×1 100 mm×50 mm的矩形板，四周螺栓连接与钢质支架栓接处为层合板.上下面板厚度约为4.8 mm，材料为高强玻璃纤维增强乙烯基(FRP)复合材料，由0°/90°交织纤维布铺设而成，每个单层厚度约为0.4 mm；芯材厚度为40 mm，材料为硬质聚氯乙烯(PVC)泡沫，见图1.

图1 复合材料夹芯板结构尺寸示意图

应变片的布置见图2.由图2可知，整块板的边缘一共用了18个沉头螺栓进行固定，并在6个加载圆面上加载.但由于对称性，理论上只有A，B，C，D，E 5个受力不同的螺栓，以及I，II 2个受力不同的加载圆面，其他部分情况和它们相同，因此，后面的分析中只对这些部分进行分析.根据应变片的方向可以看出1，2，5号应变片测的是σY，而3，4，6号应变片测的是σX.

图2 静载试验的试件尺寸和贴片方案

复合材料螺栓连接接头有限元模型见图3，复合材料板和螺栓的网格尺寸相比于加载端和支座要小很多，由于对称性，只建了1/4模型，在对称面上加对称约束.

图3 静载试验各部件有限元模型

3 多钉连接问题的有限元分析方法

很多学者都对单钉接头进行研究，主要是因为多个螺栓存在多个接触对，由于接触问题是一种高度非线性问题，这会增加计算的难度.对于上述多钉连接问题，即便采用1/4模型，仍然存在大量接触对，使得计算出现无法收敛的情况，针对这个问题，提出了3种可能解决的办法.

1) 简化接触法 这是比较常用的1种计算方法，通过简化接触对来求解，大大降低了计算的非线性和复杂性，文中通过约束可能发生接触的面来代替螺栓和支座的作用.

通过结构可能的运动方向，大致确定如下约束：螺栓A，B，C约束(图4a)中深色部分)Y方向位移，螺栓D约束(图4b)中深色部分)X和Y方向位移，螺栓E约束(图4c)中深色部分)X方向位移，还约束了板与支座接触部分的Z方向位移，见图5.

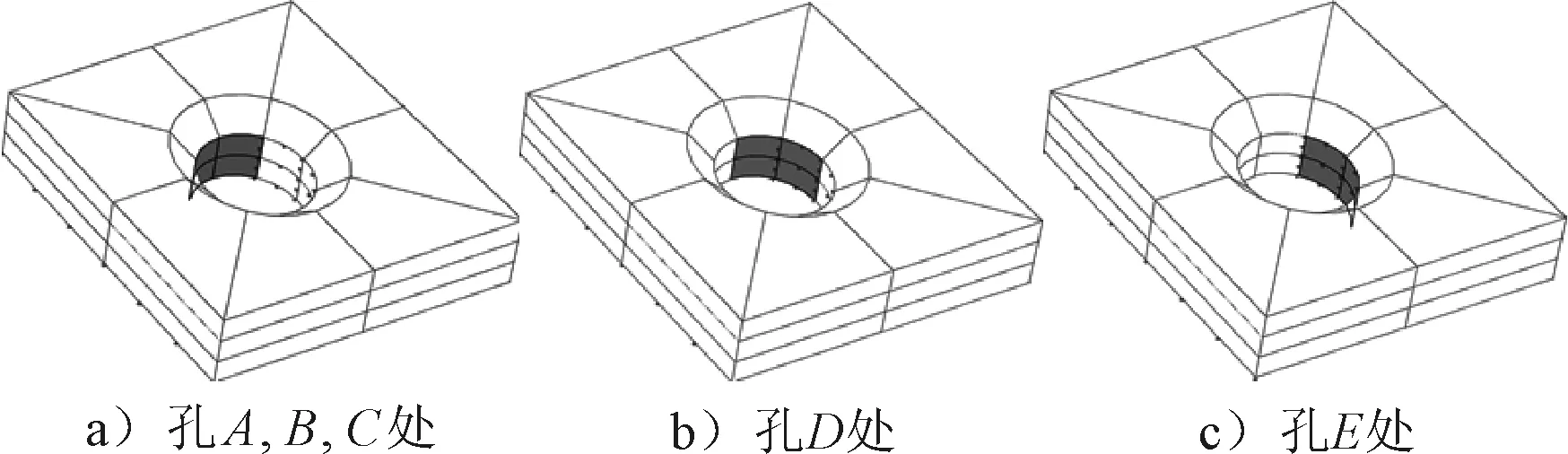
图4 简化后的约束方法

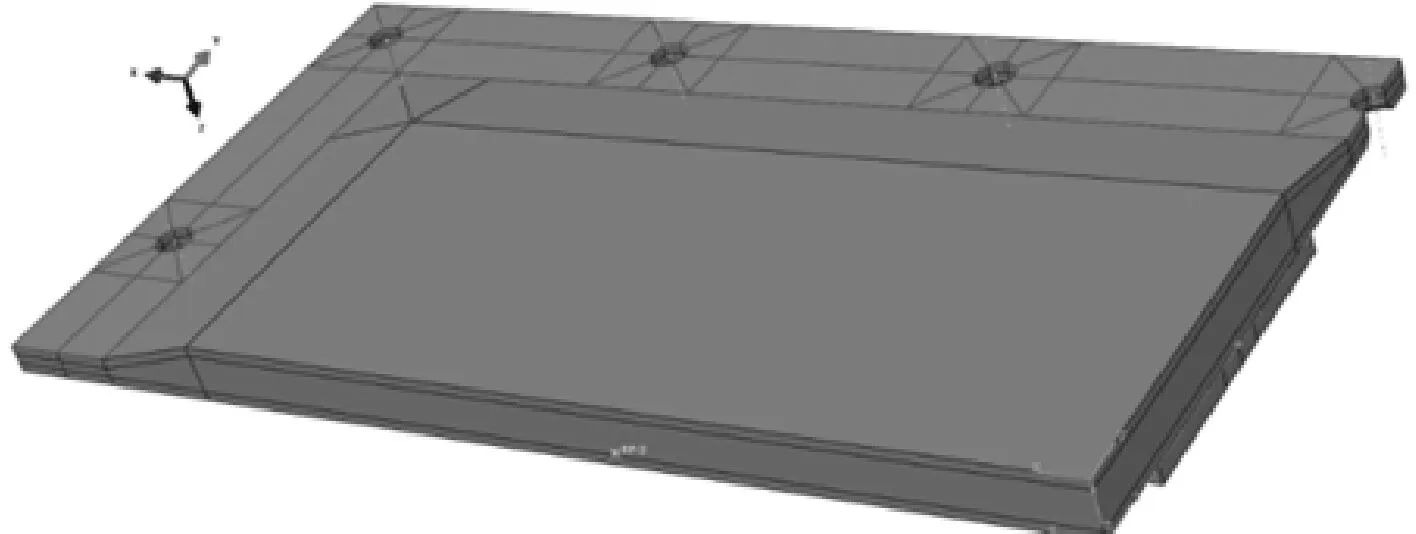
图5 复合材料板与支座的接触面

2) 插补法 实际结构涉及到多个螺栓，并不是所有螺栓都会引起结构失效.通过第1种方法确定哪些接头是危险点，只在危险的接头处加上螺栓和支座进行完整分析，根据上述方法简化其他螺栓的约束，具体操作见图6.

图6 用插补法分析螺栓E的模型

3) 准静态分析法 在结构上加1个固定载荷是静力问题，但可以认为载荷是从零逐渐增加的，当这个过程足够均匀和缓慢，就可以认为中间的每个状态都是接近平衡的，该过程便是准静态过程.理论上，当时间足够长，准静态分析的结果和静力分析的结果几乎一致.将静载试验作为准静态问题考虑，调用ABAQUS/Explicit模块，即显式分析法，这种方法一般不存在收敛问题，非常适合高度非线性问题的求解.

这种方法的关键就是加载时间的确定，文中采用Smooth幅值曲线加载，该曲线一阶导数和二阶导数都是光滑连续的，避免了加载速率变化过快导致计算不准确，模型中建立了2个分析步，分别用来施加预紧力和均布载荷，其载荷曲线见图7.2个分析步的时间都是通过试算确定的，从一个较小的时间开始，当增加到某个时间时模型上各应力分量的最大值不再出现明显变化，就以10倍的该时间作为该分析步的加载时间.

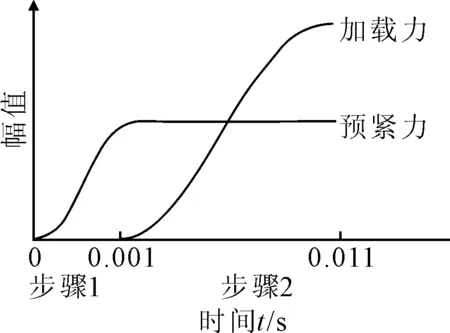
图7 预紧力和位移载荷的载荷曲线

3.1 计算结果分析

当每个加载端施加11 kN的载荷时，利用上述3种方法对各测点应力值的预测见表1，其中1号应变片与5号应变片对称，不再重复讨论.

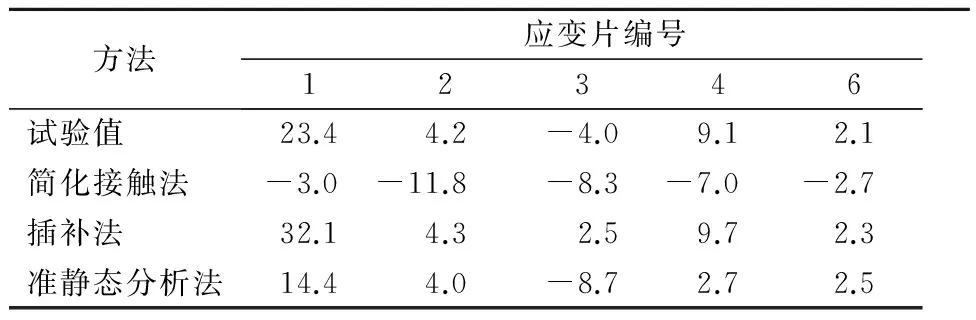
表1 3种方法与试验结果应力值对比 MPa

由表1可知，3种计算方法与实验值都存在误差，可以看到除了1号测点之外，由于2，3，4，6号测点的应力接近于0，虽然数值上看起来可能是差了几倍，实际上可以认为与实验值差距并不大，插补法和准静态分析法的数值模型是比较接近实际的，计算结果也与实验值最为接近.

3种计算方法得到的孔周应力场分布见图8～9.

简化接触法通过简化约束求解，这与接触是本质上的区别，这也是该方法与实验值存在误差的主要来源.通过简化接触对，可以大量节约计算机资源，提高计算效率，但是该方法需要准确判断两个表面之间是否发生接触，并且忽略了摩擦条件带来的影响，使得计算精度降低.

图8 3种计算方法下孔A处应力分布(单位：MPa)

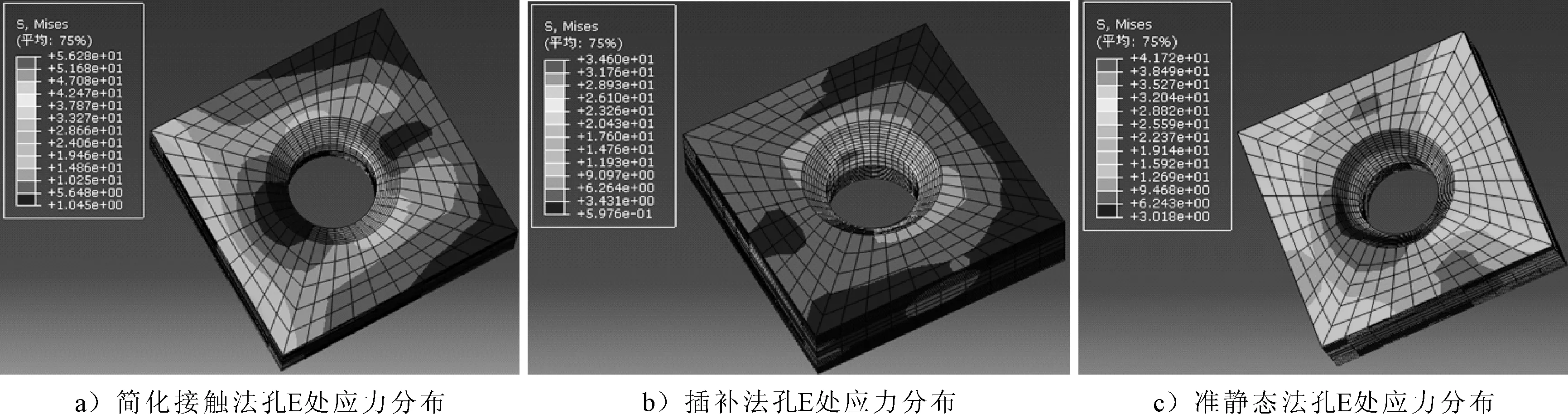
图9 3种计算方法下孔E处应力分布(单位：MPa)

插补法相对于简化接触法更加接近实际，由表1可知，计算结果比简化接触法的误差要小很多，该方法的使用范围有一定的限制，需要准确判断出危险点，代替完整的螺栓模型进行计算分析，遇到危险点较多时仍然会出现无法收敛或者计算结果不准确等情况.

准静态分析法最接近实际，考虑了所有存在的接触对，但把静载试验当做准静态过程考虑，本身就存在一定的误差，且该方法受到加载速率的影响，加载时间需要通过不断的试算来确定，计算时间也是3种方法里面最长的，但该方法使用范围广泛，非常适合复合材料多钉连接的计算求解，并且准确度较高.

考虑到测点的应力水平都不高，并且受到应变片尺寸、位置以及环境因素等影响，总的来说，插补法和准静态法都能大致反映多钉连接模型的孔周应力分布情况.

4 结 论

1) 3种方法均能模拟复合材料多钉连接，具体使用哪种方法需要对结构进行判断以及看具体需要分析什么，再来考虑使用哪种方法简单易行又不影响计算精度.

2) 若综合使用范围和计算精度来看，文中推荐使用准静态分析法来进行复合材料多钉连接孔周应力分布的相关研究.

[1]MOURITZ A, GELLERT E, BURCHILL P, et al. Review of advanced composite structures for naval ships and submarines[J].Composite Structures,2001,53(1):21-41.

[2]李成，郑艳萍，王迎佳.积分方程求解复合材料开口扳的应力分布[J].玻璃钢/复合材料，2007(1)：9-12.

[3]李成，铁瑛，郑艳萍.含复杂孔形复合材料板孔边应力场的数值分析[J].玻璃钢/复合材料，2007(8)：18-20.

[4]MCCARTHY M A, MCCARTHY C T, LAWLOR V P, et al. Three-dimensional finite element analysis of single-bolt, single-lap composite bolted joints:

part I—model development and validation[J]. Composite Structures,2005,71(2):140-158.

[5]MCCARTHY C T, MCCARTHY M A. Three-dimensional finite element analysis of single-bolt, single-lap composite bolted joints: Part II-effects of bolt-hole clearance[J]. Compos Struct，2005,71:159-175.

[6]杨杰，李威，贾红雨，等.复合材料层合板孔边应力场的有限元计算[J].玻璃钢/复合材料，2009(3):8-12.

[7]刘坤良.复合材料连接结构强度研究与失效分析[D].郑州：郑州大学，2014.

[8]周松.复合材料螺栓连接渐进损伤的实验及数值分析[D].哈尔滨：哈尔滨工程大学，2013.

[9]KRADINOV V, BARUT A, MADENCI E, et al. Bolted double-lap composite joints under mechanical and thermal loading[J]. International Journal of Solids and Structures，2001，44(38)：7801-7837.

[10]苏杰，李亚智，杨帆,等.复合材料连接件钉载分配与孔周应力解析计算[J].应用力学学报，2015,35(5)：717-724.

[11]邓培文.复合材料夹芯结构横向载荷极限强度研究及影响因素分析[D].武汉：武汉理工大学，2015.

Research on Numerical Simulation Method of Stress Distribution for Composite Multiple Bolted Joints

YAO Ye1,2)JIN Hao3)CHEN Xialiang2)ZHAO Yingjiang1,2)YAN Renjun1,2)

(KeyLaboratoryofHighPerformanceShipTechnology,MinistryofEducation,Wuhan430063,China)1)(SchoolofTransportation,WuhanUniversityofTechnology,Wuhan430063,China)2)(TheFederalHighwayAdministrationofMacheng,Macheng438300,China)3)

Based on the composite material multi-fastener joint test in the literature, this paper proposes three kinds of numerical simulation methods for calculating the hole-edge stress field of composite material multi-fastener joint by carrying out finite element analysis in ABAQUS. Through calculation and analysis, the result proves that the error of simplified contact method is larger compared with the experimental value; and the interpolation method and quasi static analysis method have relatively small error and the hole-edge stress distribution of composite material multi-fastener joint can be obtained by the two methods.

composite material; multi-fastener joint; stress field analysis; numerical simulation

2016-12-15

U664.43

10.3963/j.issn.2095-3844.2017.01.032

姚烨(1992—)：女，硕士生，主要研究领域为船舶与海洋结构物设计制造