列车交会压力波的空间分布研究*
牛纪强 周 丹 梁习锋
(中南大学交通运输工程学院轨道交通安全教育部重点实验室 长沙 410075)
列车交会压力波的空间分布研究*
牛纪强 周 丹 梁习锋
(中南大学交通运输工程学院轨道交通安全教育部重点实验室 长沙 410075)
采用三维、非定常、不可压缩雷诺时均N-S方程和Realizableκ-ε双方程湍流模型,对以350 km/h车速等速交会、350~0 km/h不等速交会和350 km/h单车运行时的3车编组高速列车气动性能进行了模拟,对比分析了车体表面和流场中的压力和速度变化.数值算法经过验证,与试验波形吻合,幅值相差不超过5%.结果表明,从列车交会侧车底到车顶,表面压力先增大后减小,峰值出现在车体凸起部位,其相对于交会侧最小压力系数区域,变化幅值可达1.76~2倍.第一个正压波峰对于距离轨面高度更为敏感,两负波幅值减小相对较小,幅值变化不超过30%.列车尾流造成的列车风较大,对空间高度十分敏感,随高度增加,列车风速度迅速减小,主要集中在半车高以下区域.列车周围不存在障碍时,列车周围流场具有时空互换性,差异主要体现在具有强非定常性流场的风挡和尾部区域.
高速列车;交会;压力波;列车风
0 引 言
随着高速列车运营速度的不断提高,2车交会时,车辆间空气受到车体壁面和地面的限制无法自由流动而受到强烈挤压,进而引起的突变压力会更加显著,列车表面不同位置处压力变化存在显著差异,这对列车车体结构疲劳及行车安全造成严重威胁[1].
国内,中南大学田红旗等[2-5]利用数值计算方法、动模型试验及在线实车试验等方法研究了列车交会问题以及影响交会压力波的因素,建立了列车交会压力波与运行速度、复线间距、车体宽度、附面层、外形,以及编组方式等之间的关系,讨论了列车交会行车安全评估方法,并提出了我国既有线上各种列车车体和车窗结构承受瞬态交会压力冲击安全运行极限值.李雪冰等[6]建立车辆系统动力学模型,研究了列车交会过程中的动力学响应,发现在列车交会过程中气动力变化剧烈,列车振动明显,尾车的振动和平稳性相对最恶劣.李人宪等[7]通过研究列车明线和隧道内等速交会对车窗的影响,发现列车明线交会和隧道内交会差异明显,相同面积的侧窗,周长大的车窗更安全,但是还需考虑玻璃抗冲击强度和安装强度.
国外对列车交会也进行了大量研究[8-10].Sanz等[11]利用1个简单的模型分析了列车风及其对行人的影响,分析了测点压力系数与车人横向距离比的敏感性、距轨道距离和行人上测点位置等相关参数及其影响.Carassale等[12]研究了列车通过时产生的气动效应和振动对线路旁设备的影响,并研究分析了设备的动力响应.Baker[13]利用缩比动模型试验和实车试验描述了明线运行列车的一系列空气动力学问题及其流场特性.Soper等[14-16]利用动模型试验研究了明线运行的集装箱货车气流发展和流场特性,分析了关键区域流场的气流和压力,在集装箱货车头部和尾部流场区域的列车风和压力相对其他客车要大,货车的附面层厚度显著增加且内部处于强湍流度状态.文中模拟了明线单列车运行和2列3车编组高速列车以不同组合速度交会,对比分析了车体表面交会压力波幅值分布,以及交会侧空间压力和速度分布,列车运行工况见表1.

表1 计算工况
1 模 型
1.1 数学模型
数值计算中车速Vt=350 km/h,马赫数接近0.3,列车交会时相对车速已超过0.6马赫,车体间气流受到地面、和车体间的限制,无法自由流动而受到强烈挤压,需要考虑气体的可压缩性.模型列车高度H视为特征长度,此时列车周围流场雷诺数一般大于1×105,即列车周围流场处于强湍流状态.本次计算,采用Realizableκ-ε湍流模型求解整个流场.
文中计算基于Fluent,采用Realizableκ-ε湍流模型,速度压力耦合采用PISO算法,对流项采用一阶迎风格式离散,扩散项采用QUICK格式离散,时间采用二阶隐式格式推进..
1.2 计算模型
模拟计算中采用头车(6.88H)+中间车(6.6H)+尾车(6.88H)3车编组、缩比1∶8的高速列车作为计算模型,总长20.65H,H为车高,列车模型见图1.

图1 列车模型
在节约计算资源和不影响主要关心区域流场结构的前提下,对列车和受电弓模型表面做了必要且合理的简化,省略了车体表面的扶手、受电弓等部件.对流线型车体、转向架、风档等结构相对较复杂的区域网格进行局部加密处理.远离列车区域对受电弓气动力及其周围流场结构影响有限,设置相对较为稀疏,空间体网格3 000万以上.图2为列车表面网格.
图2 列车表面网格
2 计算域及边界条件
2.1 计算域
为保证列车在交会时,列车周围流场已充分发展,避免边界对列车周围流场结构影响.计算域X方向长147H,Y方向宽为50H,Z方向高为20H.两车头部鼻尖点距入口边界27H,为避免出口边界条件对列车流场及尾涡变化的影响,尾涡区域长40H.列车计算区域见图3.

图3 计算域及边界条件
2.2 边界条件
对计算域的边界进行设置,以便获得唯一解,计算流域边界设置见图3.列车表面给定无滑移壁面边界条件,两车体流域均设置为滑移网格,其速度设置为:X方向速度分量为列车运行速度Vt和-Vt,Y方向速度分量和Z方向速度分量均为0;流域前、后端面和顶面设置为基于黎曼不变量的远场边界条件,相对压强pout=0 Pa;流域两侧面采用对称边界条件.地面给定无滑移固壁边界条件,车体和地面近壁面区域流场采用标准壁面函数控制模拟.
2.3 测点布置
本次数值模拟车体表面测点主要布置在距离鼻尖4.9H处的截面S1,S3和距离鼻尖10.3H的S2截面上的line-1上;距离轨面高Z=0.254H处的车体水平截面line-2上;流场空间测点布置在两轨距中心线line-3上的从轨面到1.08H范围内.line-1上相邻测点间隔0.0254H;line-2相邻测点间隔0.27H;line-3上布置了13个测点,监测了列车风和压力变化.测点布置示意图见图4.
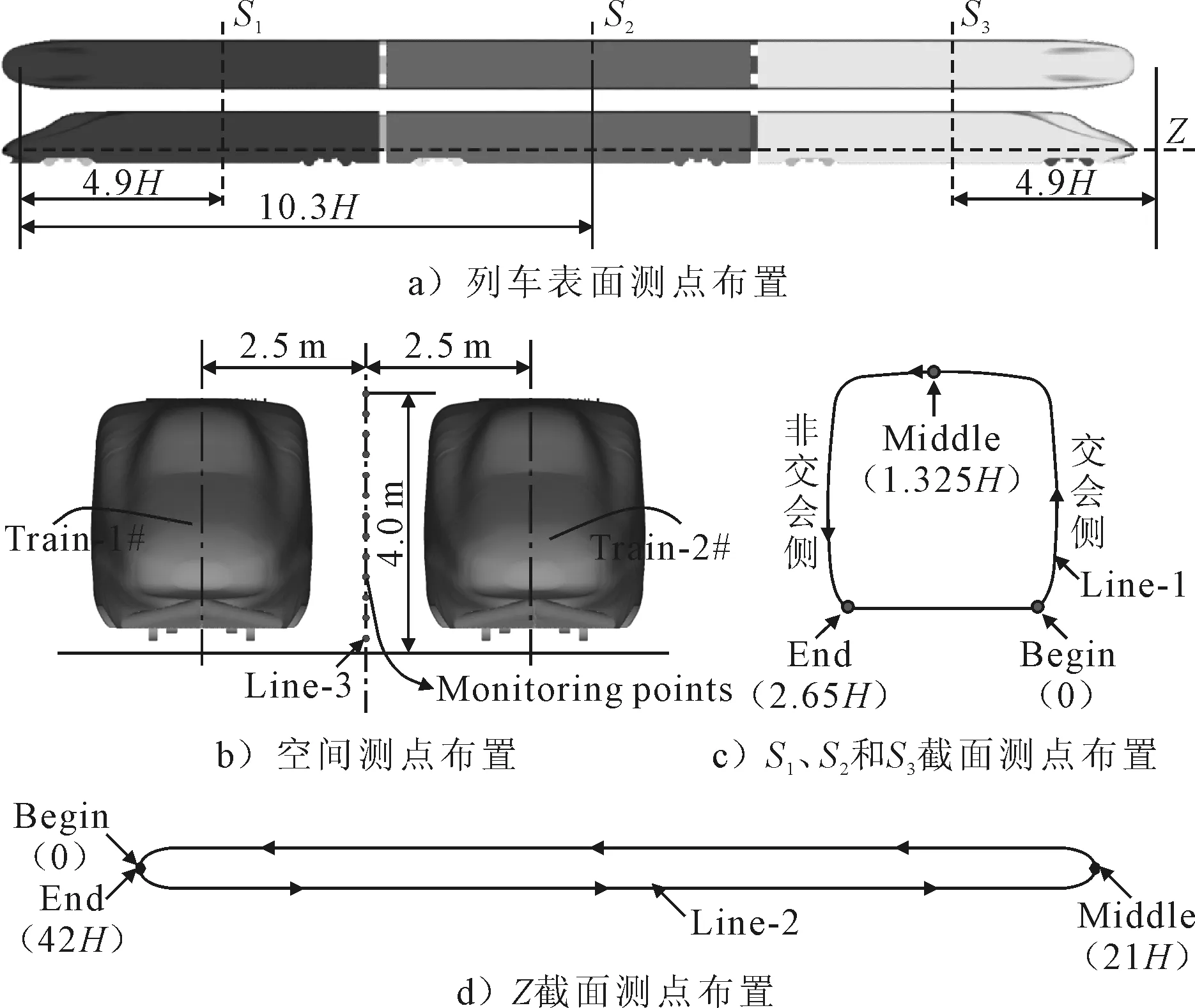
图4 监测点布置示意图
3 算法验证
试验采用缩比1∶20的头车+中间车+尾车3车编组的高速列车模型,试验速度为350 km/h,于“列车空气动力特性动模型试验系统”上进行缩比试验,如图5所示.

图5 高速列车模型
建立与动模型试验一致的数值计算模型,文中选取距列车S2截面上距离起始点0.59H处测点作为试验和数值计算对比测点.图6为高速列车模型以350 km/h车速等速交会,车体表面测点监测得到的交会压力波的动模型试验与数值模拟计算结果对比.由图6可知,交会压力波的计算波形与动模型试验所得数据有较高的吻合度,且两者幅值偏差不超过5%,满足工程应用要求.

图6 数值计算与动模型试验结果对比
4 结果与分析
为便于分析,各气动压力系数定义如下.
(4)
式中:ρ为空气密度,1.225 kg/m3;p为测点压力;p∞为无穷远处压力;Ui为列车风,分别代表X,Y,Z3个方向和合成风;Cp为压力系数.
为便于分析,定义Cpmax,Cpmin和CΔp分别为车体表面各处交变压力波系数Cp的最大值、最小值和峰峰值.
4.1 车体表面压力系数分析
图7为列车按方案C1和C2交会时,S1,S2和S3截面处交会压力波Cpmax、Cpmin和CΔp沿Line-1分布.C1和C2的不同截面处的列车表面Cp沿Line-1的分布一致.相对C2而言,C1下的列车表面压力系数沿Line-1分布有明显波动,且不同截面处压力峰值有明显差异.由图7a)可知,C1和C2的非交会侧列车表面交会压力系数正峰值差异相对较大.由图7b)可知,C2下的车体各截面处交会压力波系数负峰值整体偏大.由图7c)中可知,C1和C2的列车交会侧中下部区域Cp变化幅值差异明显,C1显著大于C2,这可能是两列车间靠近地面区域的空气流动受限,并受到高速运行列车的强烈挤压而引起交会冲击压力增大.对比C1和C2不同横截面处的车体表面压力系数可知,车体运行形成的附面层和列车周围的涡脱降低了交会压力波正峰值,增加了交会压力波负峰值.

图7 列车表面交会压力波系数幅值沿Line-1分布
由图7还可看出,列车交会侧车体表面Cp沿Line-1(0~0.9H)变化显著,随高度增加,压力先增大后减小.在交会侧区域(0~0.9H),相对于交会侧最小Cp位置处,列车交会侧其他位置处Cpmax,Cpmin和CΔp的最大增幅分别2.27~3.37倍,1.4~1.51倍,1.76~2倍.
图8为列车按C1和C2交会时,列车Z截面处交会压力波系数Cpmax,Cpmin和CΔp沿Line-2分布.由图8a)和b)可知,车体表面交会压力波系数在头尾流线型、风挡区域有显著差异外,等截面车体区域的表面压力系数基本一致.从图8c)可知,C1和C2下的Line-2上车体表面压力系数变化幅值分布规律一致,C1交会侧车体表面CΔp明显大于C2,且C1的Line-2上压力系数分布波动明显.对比C1和C2车体表面压力系数分布可知,对于运行与静止的列车表面下部区域压力变化的差异主要在流线型和风挡区域,这是由于测点与交会列车壁面距离不同和列车运行时风挡周围流场结构改变引起的.列车交会侧表面压力变化幅值差异主要是由C1工况中两交会列车相向运行造成的列车间空气受挤压程度强于C2引起的.

图8 列车表面交会压力波幅值沿Line-2分布
4.2 流场压力及速度分析
图9为列车按C1及C2交会和按C3运行时,空间压力系数Cpmax,Cpmin和CΔp沿Line-3分布.由图9可知,3种工况下Line-3上的压力系数Cpmax,Cpmin和CΔp均随离轨面高度增大而减小,且三种工况之间差异显著.C1产生的压力系数峰值及变化幅值最大;C1和C2中的Cpmax分别比C3增加1.23~1.75倍和26%~43%;C1和C2中的Cpmin分别比C3增加0.67~1.27倍和12%~33%;C1和C2中的CΔp分别比C3增加1.11~1.4倍和21%~38%.C3工况中列车周围气体不受限制可以自由流动;C2工况中交会侧有一静止的列车,车体和地面限制了Line-3所在区域空气流动,气流受到强烈挤压,进而引起压力增加;C1工况中相向运行的两列车周围高速流动的气流也发生碰撞,加剧了Line-3所在区域气体的挤压,导致压力显著增大.
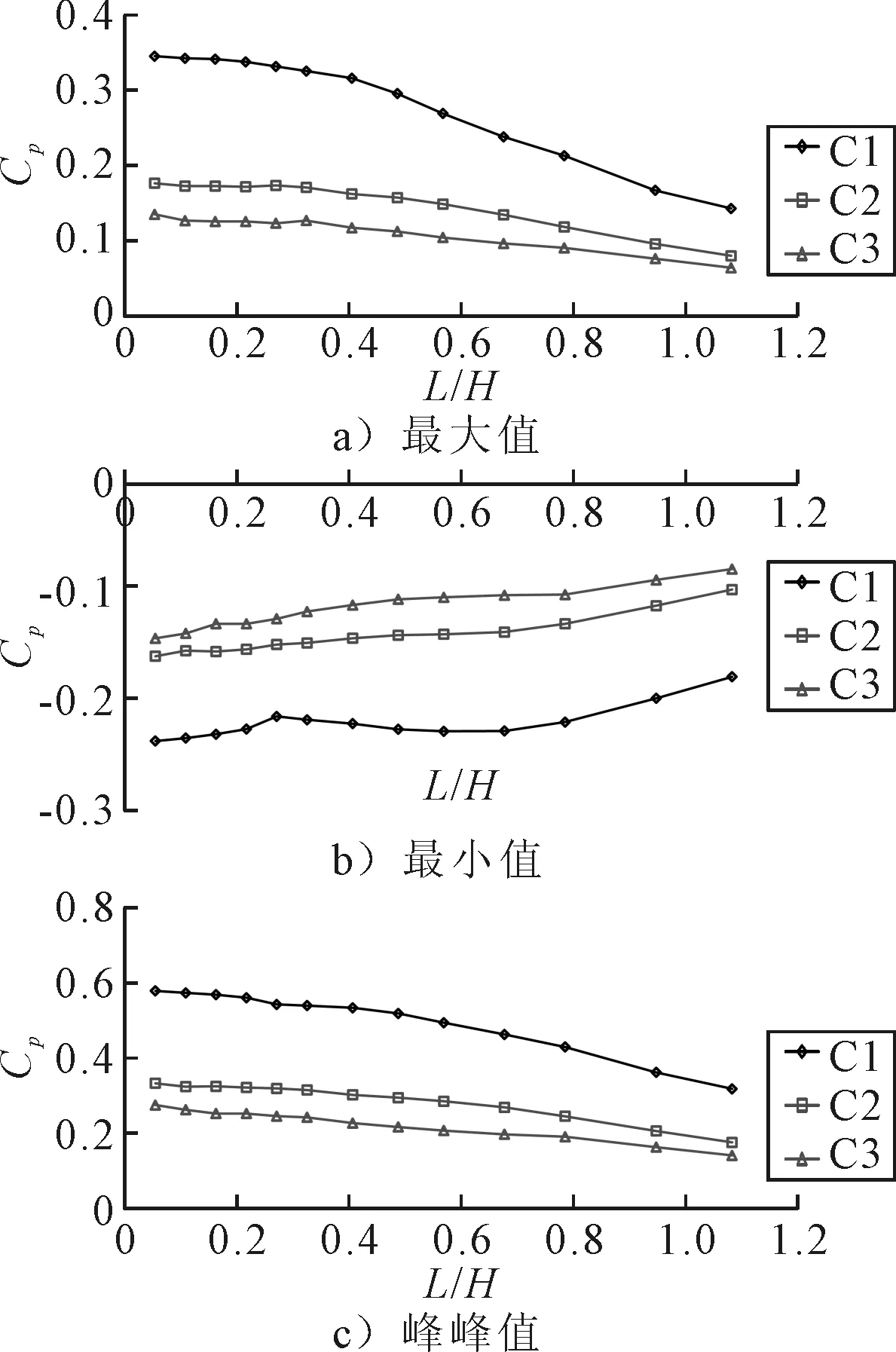
图9 空间压力系数变化幅值沿Line-3分布
图10为C1工况下的Line-3上距轨面不同高度处测点压力变化曲线.由图10可知,列车在Line-3所在位置处等速交会时,Line-3上各测点压力系数变化波形一致,幅值随距离轨面高度增加而显著减小;从0.05H到0.7H高度,2正波峰幅值减小了50%左右,而第1个正波峰对距离轨面高度更为敏感些,这是由于头尾车鼻尖引起的交会压力正波峰,而鼻尖点位于0.3H附近;两负波峰的幅值减小不超过30%,这由于引起负压力波是列车流线型过渡段区域,涵盖了整个列车车高.图11为列车周围压力分布.由图11可知,鼻尖区域处于较大正压区,头尾车流线型过渡区域处于较大的负压区.

图10 沿Line-3部分测点压力变化曲线

图11 高速列车周围流场
图12为列车按C1,C2交会和按C3运行时,列车风3个方向分量变化的最大值、最小值和峰峰值沿Line-3分布.由图12可知,Line-3上各测点列车风x方向分量变化规律基本一致,均随距离轨面高度增加而减小,其中C1显著小于C2和C3;在靠近轨面区域的C2和C3的列车风x方向相接近.列车交会时列车周围气流相向流动,且相互阻滞,降低了气流流动速度.Line-3上测点的列车风y方向分量变化规律有一定差异,由于列车相向运行, 相对Line-3所在平面,流场呈对称分布,由于列车相向运行而产生的相向流动的气流,导致C1中列车风y方向分量基本为0;C2中一列车运行,另一列车静止,从而形成非对称流场,交会侧区域下部气流受静止列车限制导致y方向流速相对较低,此区域气流被挤向列车交会侧上方,引起交会侧上部气流流速增加;由于C3工况中列车周围气流可自由流动,产生的列车风y方向分量相对较大.从列车风z方向分量沿Line-3的分布可知,列车交会明显将列车交会侧气流挤向上方,列车交会后气流又被两列车离开后形成的尾流吸回;C2工况中列车交会侧气流受挤压程度相对C1弱,C3工况下列车周围气流自由流动,列车风z向分量更小.
图13为C1工况下的Line-3上不同高度处测点列车风在列车运行方向分量的时程曲线.由图13可知,列车尾流造成的列车风较大,而列车尾部区域列车风差异明显,随高度增加,列车风速度显著减小,低于0.4H区域的列车风相对较大,这说明列车尾流主要集中在列车0.4H以下区域.
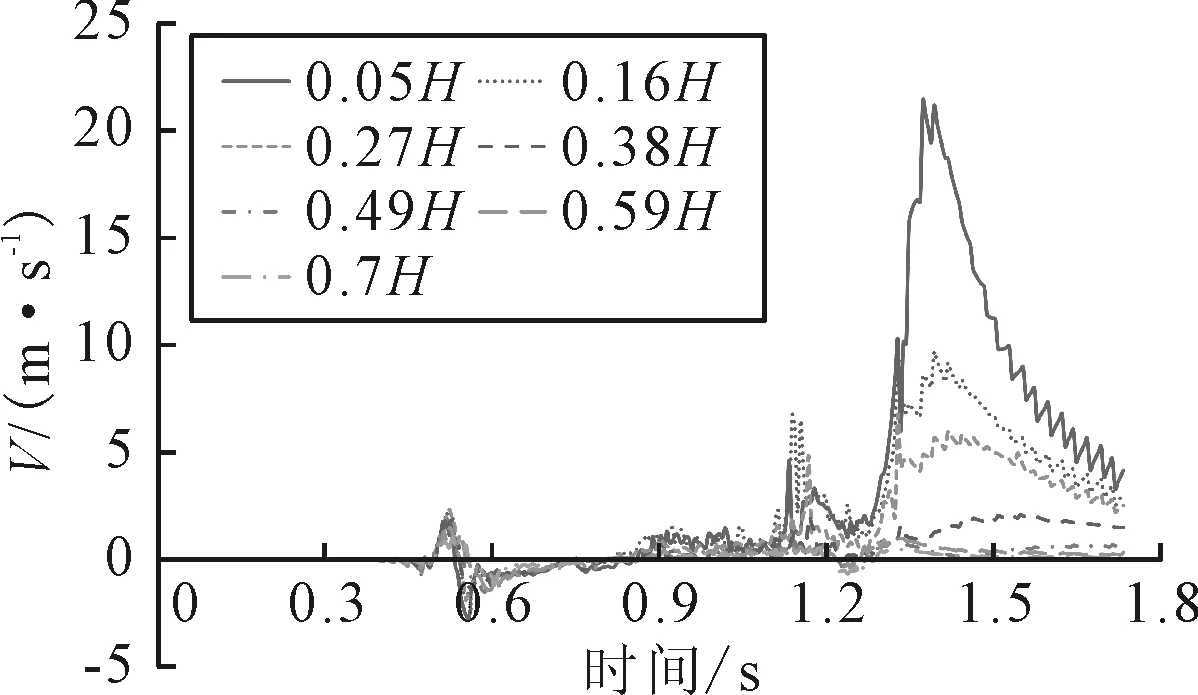
图13 Line-3上部分测点列车风x方向分量时程曲线
图14为列车周围流场压力的空间分布和时间历程对比.其中p1为列车通过位于Line-3上距轨面1 m高处测点时的压力变化,p3为列车通过一静止列车时,静止列车Train-2交会侧车体表面距轨面1 m高处测点压力变化;p2和p4分别为瞬态下沿p1和p3测点所在与列车运行方向平行的直线上的压力分布.为便于对比,对压力的空间和时间坐标进行了无量纲化.由图14a)可知,p1和p2幅值相差不超过5%,波形吻合度高,由此可知,明线列车周围固定点的非定常压力变化与该点所在与列车运行方向平行的直线上的压力分布一致.由图14b)可知,p3和p4波形吻合度相对较高,但是幅值相差超过30%,这是由于Train-1通过静止Train-2时,交会侧空气受到强烈挤压,导致此区域压力变化相对较大,引起Train-2车体表面压力波动较大.从图中可知列车尾部区域压力曲线有较大差异,这是由于列车尾涡流场具有强非定常性,从而导致列车周围瞬态流场的压力分布与相应位置处测点的非定常压力波动具有明显差异.列车周围存在的障碍,对波形影响相对较小,对幅值影响较大.因此,在一定程度上,列车周围流场空间分布和时间分布可相互转换,即列车时空互换性.

图14 列车周围压力分布对比
5 结 论
1) 列车不同截面处交会压力波峰值有一定差异,沿车体向后波形存在整体下移趋势,对交会压力波变化幅值影响很小.列车运行时形成的附面层和列车周围的涡脱降低了交会压力波正峰值,增加了其负峰值.交会侧底部区域气体受挤压相对严重,从车底到车顶,交会侧车体表面压力先增大后减小,峰值处对应车体凸起部位,其相对于交会侧最小压力系数区域,变化幅值可达1.76~2倍.
2) 相对交会压力中其它波峰,第1个正压波峰对于距离轨面高度更为敏感,这是由于列车鼻尖区域的正压引起的交会压力波两正波,而鼻尖点位于30%的车高附近;2负波幅值减小相对较小,幅值变化不超过30%,这由于引起负压力波是列车流线型过渡段区域,涵盖了整个列车车高.
3) 列车尾流造成的列车风较大,对空间高度十分敏感,随高度增加,列车风速度迅速减小,主要集中在半车高以下区域.
[1]RAGHUNATHAN R S, KIM H D, SETOGUCHI T. Aerodynamics of high-speed railway train[J]. Progress in Aerospace Sciences,2002,38(6):469-514.
[2]田红旗.列车交会空气压力波研究及应用[J].铁道科学与工程学报,2004(1):83-89.
[3]田红旗,许平,梁习锋,等.列车交会压力波与运行速度的关系[J].中国铁道科学,2006,27(6):64-67.
[4]刘堂红,田红旗,鲁寨军.列车交会压力波对高速磁浮列车横向动态响应的影响分析[J].中国铁道科学,2004,25(6):9-14.
[5]熊小慧,梁习锋.CRH2型动车组列车交会空气压力波试验分析[J].铁道学报,2009,31(6):15-20.
[6]李雪冰,侯传伦,张曙光,等.高速列车交会时的风致振动研究[J].振动与冲击,2009,28(7):81-84.
[7]李人宪,赵晶,刘杰,等.高速列车会车压力波对侧窗的影响[J].机械工程学报,2010,46(4):87-92.
[8]FUJII K, OGAWA T. Aerodynamics of high speed trains passing by each other[J]. Computers & Fluids,1995,24(8):897-908.
[9]HERMANNS L, GIMÉNEZ J G, ALARCN E. Efficient computation of the pressures developed during high-speed train passing events[J]. Computers & Structures,2005,83:793-803.
[10]UYSTEPRUYST D, KRAJNOVI S. Numerical simulation of the transient aerodynamic phenomena induced by passing manoeuvres[J]. Journal of Wind Engineering & Industrial Aerodynamics,2013,114(2):62-71.
[11]SANZ A A, SANTIAGO P J. Train-induced pressure on pedestrians[J]. Journal of Wind Engineering & Industrial Aerodynamics,2002,90:1007-1015.[12]CARASSALE L, MICHELA MARRBRUNENGHI. Dynamic response of trackside structures due to the aerodynamic effects produced by passing trains[J]. Journal of Wind Engineering & Industrial Aerodynamics,2013,123(1):317-324.
[13]BAKER C J.The flow around high speed trains[J].Journal of Wind Engineering&Industrial Aerodynamics,2010,98(6):277-298.
[14]SOPER D, BAKER C, STERLING M. Experimental investigation of the slipstream development around a container freight train using a moving model facility[J]. Journal of Wind Engineering & Industrial Aerodynamics,2014,135:105-117.
[15]LAM W, HAMILL G A, ROBINSONS D J, et al. Experimental investigation of the decay from a ship’s propeller[J]. China Ocean Engineering,2011(6):386-391.
[16]YEH P H, CHANG K A, HENRIKSEN J, et al. Large-scale laboratory experiment on erosion of sand beds by moving circular vertical jets[J]. Ocean Engineering,2009(1):47-52.
Study on Spatial Distribution of Instantaneous Pressure Pulse Caused by Two Meeting Trains
NIU Jiqiang ZHOU Dan LIANG Xifeng
(KeyLaboratoryofTrafficSafetyonTrack,MinistryofEducation,SchoolofTraffic&TransportationEngineering,CentralSouthUniversity,Changsha410075,China)
Based on the three-dimensional unsteady compressible Reynolds-averaged N-S equation and the Realizableκ-εdual equation turbulence model, the aerodynamic performances of the three marshalling high-speed trains, running at speed of 350 km/h, passing each other at the same speed (350 km/h) or passing each other at the different speed (35 0km/h and 0 km/h), are simulated. The pressure and velocity change of the train surface and in the flow field are compared and analyzed. Numerical algorithm is verified with experiments in this paper. The wave profile obtained in numerical simulation agrees well with the one of experiments, and the difference between them is below 5%. From the bottom to the top of the train intersection, the surface pressure increases first and then decreases. The maximum of pressure change appears at the raised part of train body and can reach to 1.76~2 times of the minimum pressure. The first positive pressure wave is more sensitive to the distance between the monitoring point and the rail surface. The decrease of two negative pressure waves is relatively small, which is no more than 30%. The gust induced by the wake is the most dramatic, which is very sensitive to the height. The velocity of gust rapidly decreases with the increase of height. The train gust is mainly concentrated in the area of the half car height. When train running in open air, the flow field around the train has space-time interchangeability and the difference is mainly reflected in strong unsteady flow around windshield and tail car.
high-speed train; two meeting trains; instantaneous pressure wave; train gust
2016-10-29
*高铁联合基金项目(U1134203、U1334205)、湖南省研究生科研创新项目(CX2015B046)资助
U266
10.3963/j.issn.2095-3844.2017.01.012
牛纪强(1988—):男,博士生,主要研究领域为列车空气动力学

