改进变邻域搜索算法在求解VRPMT的应用*

宋 强 杜暖男

(广东理工学院信息工程系1) 526100 肇庆) (平顶山工业职业技术学院计算机与软件工程学院2) 平顶山 467001)

改进变邻域搜索算法在求解VRPMT的应用*

宋 强1)杜暖男2)

(广东理工学院信息工程系1)526100 肇庆) (平顶山工业职业技术学院计算机与软件工程学院2)平顶山 467001)

多行程车辆路径问题是标准车辆路径问题的一个变体，每个车辆在运行期间可以使用不止一次.对于这种NP-HARD问题，提出了1个改进变邻域搜索算法并设计了4个邻域结构用于求解和制定多行程路径问题的调度规划.该算法测试了1组标准实例问题，获得的解决方法与文献中提出的5种算法进行比较，并得到了较好的结果.

车辆路径问题；多行程；变邻域搜索；抖动

0 引 言

标准的车辆路径问题(vehicle routing problem，VRP)指的是具有一定容量的相同车辆访问或者交付货物给若干客户.其目的是对车辆行程进行规划，以最小化总成本 (如行驶时间、行驶距离等)来服务和满足所有客户需求.每个客户必须只能被访问1次，每个行程必须开始和结束于仓库.每辆车的交付货物的数量不得超过车辆的容量，行驶距离不得超过预先定义的范围.

文中主要研究了多行程车辆路径问题(vehicle routing problem with multiple trips，VRPMT)，这是标准VRP的一个变种，特点是每辆车在工作期间可以使用不止1次.

针对多行程车辆路径问题的研究，国内研究文献较少.宋强等[1]为了同时解决多行程车辆路径问题和配送中心定位问题，采用模拟退火的逻辑和交换算法来获得最优路线，并改善了模拟退火算法中当前温度控制的位置.张媛媛等[2]研究了多行程带时间窗口的车辆调度问题，设计了计算路线时间窗口的具体数学模型，并且通过数学推导证明了该时间窗口是等待费用最小的服务时间窗口.许争争等[3]考虑车辆容量和绕行时间限制等因素提出了1种基于协作的3阶段算法，通过案例分析证明了该方法可以更好的提供车辆调度方案.在国外，Fleischmann[4]首先对这个VRPMT进行了研究，他针对著名的节约算法提出了1个修改方法和一个装箱启发式算法.之后许多文献都提出了启发式算法解决问题，如3段论启发式算法、禁忌搜索算法、1个多阶段构建的启发式算法、基于自适应记忆过程修改的启发式算法及一个混合遗传算法[5-9].但是，以上文献中没有研究人员采用改进变邻域算法对这个问题进行相应的研究.

变邻域搜索算法主要由邻域转换机制(抖动)和局部搜索算法组成[10].变邻域算法的特点是容易找到当前解域范围内的最优解.其中局部搜索算法构造了只接受更优解作为下1次操作的个体，是1种功能强大的局部探索过程，而抖动不考虑解的优劣，只要满足条件即可，很容易产生更多未探索过的新解.两者结合达到某种平衡就能找到所有问题的全局最优解.

基于此，很多研究采用变邻域算法来求解各种问题.张晓楠等[11]采用变邻域分散搜索算法来求解同时配集货的定位-路线问题，在保留组合策略的全局搜索能力的基础上，再运用变邻域搜索算法进行局部开发来提高可行解质量.潘全科等[12]为了解决作业车间调度问题，充分利用了粒子群算法和变邻域搜索算法的互补性能，提出1种新的粒子群-变邻域搜索的混合算法.戈军等[13]采用聚类方法完成客户分配和路线规划的初始解构建，设计了最佳改进策略实现算法以获得在求解质量和运行时间上的最佳平衡.

文中提出了1种改进变邻域搜索算法(variable neighborhood search，VNS)来解决VRPMT，在该算法中，采用4个不同的邻域结构，其中2个用于最小化行程总长度和超时，另外2个用于最小化超时.在抖动步骤中，在概率分布的基础上采用了3种类型的邻域，通过比较研究，结果说明提出的算法优越于其他研究方法.

1 用于VRPMT的变邻域搜索

1.1 符号定义

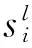
车辆i的超时由下列表达式给出

max(0,DTi-T)

(1)

最长行驶比率(LTR)用于提供现有方案中的最长(最差的)超时.

(2)

1.2 方案展示

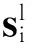
1.3 初始解

1.4 评价函数

提出的目标函数类似于文献[8]提出的函数.它是采用1个由总行驶时间、超时和超容量惩罚的相关计算得到的1个动态的函数.

α和β参数以动态的方式进行调整，以较小的步骤进行邻域扩展，并增加插入和交换的移动能力.

(4)

1.5 变邻域下降算法

该变邻域下降算法采用4个邻域结构(N1，N2，N3和N4)寻找每辆车每个行程的最佳客户配置.邻域算符N1包括4种插入位移.从位置i移动1个客户插入到位置j: ①在同1行程；②在相同车辆的另1个行程；③在另1辆车的另1个行程；④第4次移动，从位置i移除1个客户，并将它插入到相同车辆或另1个车辆新创建的行程中.第2个邻域结构N2从车辆i中移除1个行程k并把它插入车辆j.第3和第4邻域结构(N3，N4)交换移动过程.邻域结构N3采用3次移动交换，分别是：①2个客户在同1个行程内的位置交换；②相同车辆的2个不同行程的客户交换；③来自2个不同车辆的2个行程内的2个客户交换.第4邻域N4互换2个不同车辆的2个行程.领域结构N1和N3用于最小化多个行程和超时时间的总长度.而邻域结构N2和N4用于最小化超时时间.提出的可变邻域下降算法的步骤见算法1.

算法1 变邻域下降算法(VND)

Input：邻域集合Nh，h=1,2，…,hmax=4

Initialization：找一个初始解s；

Repeat

h←1;

Whileh≤hmaxdo

s′←s的最佳邻域， s′∈Nh(s)

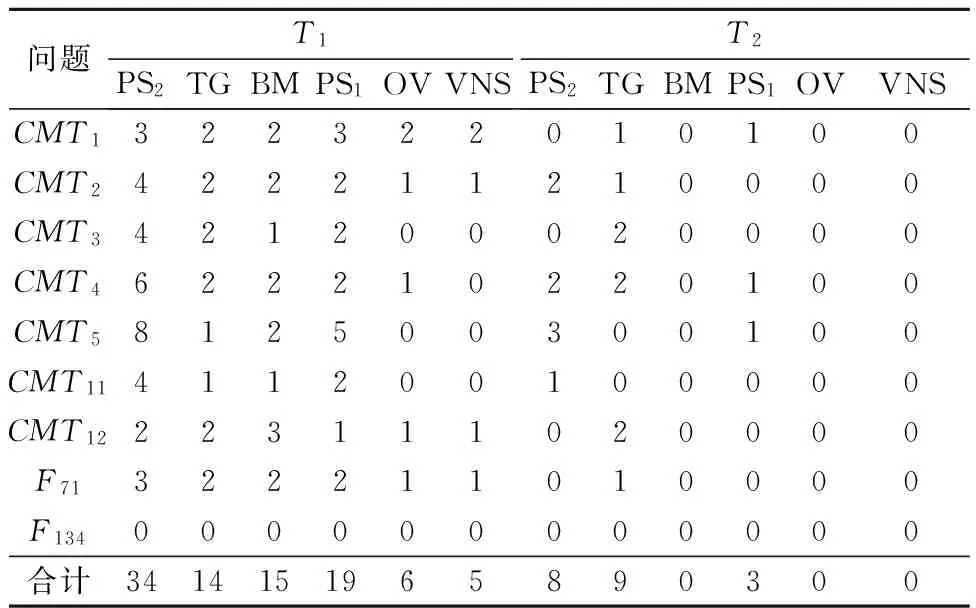
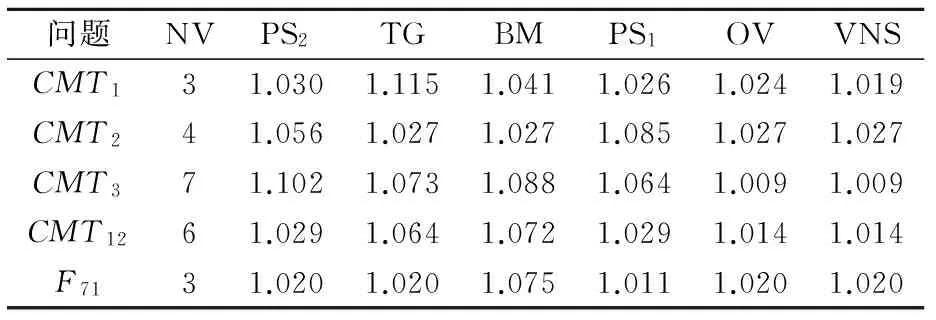
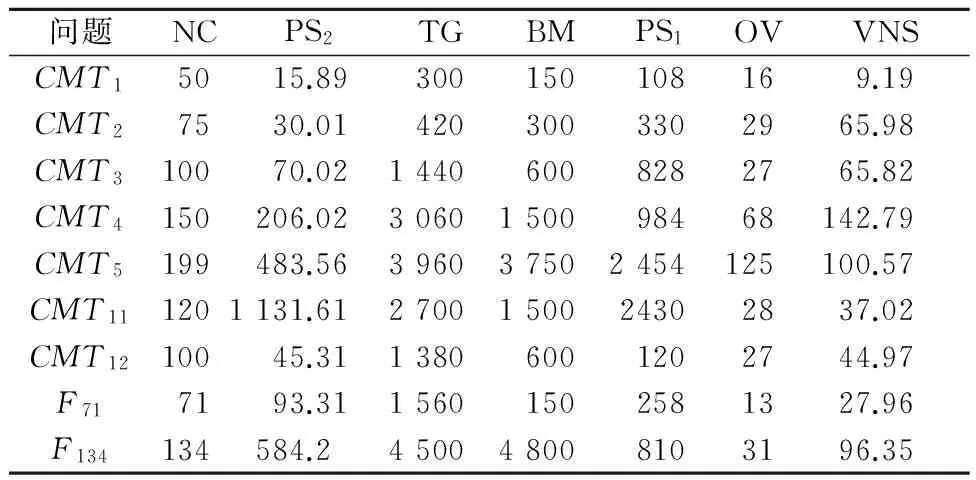
Iff(s′)

s←s′;

h←1;

else

h←h+1

endif

endwhile

until不能获得任何改进为止

returns;

1.6 抖动

给定1个邻域结构N，Nm表示在邻域N中的第m个连续的移动.在抖动步骤中，将m次移动应用到邻域(N1,N3和N4).对于每1个从1到m的i 的取值，我们将选择1个基于概率Pk分布的邻域结构Nk(k∈{1,3,4})，进行随机的移动.

1.7 变邻域搜索

该变邻域搜索算法的主要步骤是：初始化，抖动，用变邻域下降(variableneighborhooddescent，VND)算法进行局部搜索和评估，这些步骤见算法2.

算法2 变邻域下降算法(VND)

Input: 邻域集合Nh，h=1,2，…,hmax，

Initialization: 找一个初始解s;

Repeat

h←1;

Whileh≤hmaxdo

s′←对s进行抖动，

s″←VND(s′)

Iff(s″)

s←s″;

h←1;

else

h←h+1

endif

endwhile

until符合终止条件A

returns;

首先从初始解决方案s开始，接下来，通过对方案s执行抖动步骤设计1个解决方案s′，该解决方案将作为VND算法寻找1个局部最优s″的基础.在评价步骤中，如果f(s″)

2 计算结果

该改进VNS算法采用来自Christofides改编的VRP数据集进行测试.相关的算法采用C++语言编写，并在戴尔笔记本电脑T2130@1.86GHz，1GRAM上运行.采用了由文献[5-9]等发现的标准进行比较研究，采用发明人的姓名缩写分别简称为TG，BM，PS1，OV和PS2，并结合最长行驶比(LTR)对结果进行比较.在程序运行的基础上，设定以下参数用于生成计算结果，α∈(0.001,0.999)，ε1=0.001，β∈[1，100]，ε2=0.01.在抖动过程中，在邻域(N1，N3和N4)执行hmax=3的移动，并分别选择概率为0.6，0.4和0.2.

通过表1看到，VNS算法能够在104个样例中的99个样例中找出可行的解决方案，包括任意1个早期工作都无法解决的实例.对于算法PS1，TG，BM和PS2，几乎所有的算法在解决带时间T1的标准样例时都遇到了一些困难，解决方案的成功率低于73%.而算法VNS和OV的成功率明显优于其他算法，分别为90.38%和88.46%.

表1 通过改进VNS算法和其他标准找到的可行解的数量

在表2展示了提出的算法，以及上面提到的其他文献中都不能找到可行解的标准样例的数量. 表2利用LTR比率说明了比较结果，其中在每个标准样例中该VNS算法都无法找到可行解.从这些结果我们注意到从5个未解决的标准样例中该改进VNS算法提供了4个样例的最佳解决方案，其次是OV算法也提供了和VNS算法相同的结果，CMT1实例稍差些.BM算法提供的F71实例也获得了最佳结果.

表2 用于不可行解决方案的最长行驶比(LTR)的比较

表3给出了针对每个实例的5次比较的平均CPU时间.表4为当NV=7和T=154时CMT4新的可行解.结果表明，该VNS算法在解决这些标准实例时相对较快.

表3 平均CPU时间 s

表4 当NV=7和T=154时CMT4新的可行解

最后，基于以上提供的不同结果，考虑到能够找到可行解的标准实例的数量，求解的质量以及寻找分配的CPU时间，该算法相比其他算法是很有竞争力的，它可以归类为解决VRPMT问题的最佳算法.

3 结 束 语

提出1种改进变邻域搜索算法(VNS)来解决带多行程的车辆路径问题.采用4个不同的邻域结构，其中2个用于最小化行程总长度和超时，另外2个用于最小化超时.在抖动步骤中，在概率分布的基础上采用了3种类型的邻域.比较研究表明，该算法与其他文献中的结果相比提供了较高质量的求解结果，说明本文提出的算法优越于其他研究方法.在未来的工作中，该算法可以扩展到求解混合车辆的车队问题或带多车厢的车辆路径问题.

[1]宋强,刘凌霞.多行程车辆路径问题和配送中心定位问题的研究[J].数学的实践与认识,2016,46(7):103-113.

[2]张媛媛,曾晓燕.多行程带时间窗的车辆调度问题研究[J].数学的实践与认识,2015,45(7):1-7.

[3]许争争,唐加福.基于协作的三阶段启发式算法求解多行程车辆行程问题[J].南开大学学报(自然科学版),2015,48(5):51-59.

[4]FLEISCHMANN B. The vehicle routing problem with multiple use of vehicles[J].Working Paper, Fachbereich Wirschaftswissenschaften,1990(1):55-58.

[5]TAILLARD E, LAPORTEV G,GENDREAU M. Vehicle routing problem with multiple use of vehicles[J]. Journal of the Operational Research Society,1996,47(8):1065-1070.

[6]BRANDAO J, MERCER A. The multi-trip vehicle routing problem[J].Journal of the Operational Research Society,1998,49(8):799-805.

[7]PETCH R J, SALHI S. A multi-phase constructive heuristic for the vehicle routing problems with multiple trips[J]. Discrete Applied Mathematics,2003,133(1):69-92.

[8]OLIVERA A, VIERA O. Adaptive memory programming for the vehicle routing problem with multiple trips[J]. Computers & Operations Research,2007,34(1):28-47.

[9]SALHI S, PETCH R J.A GA based heuristic for the vehicle routing problem with multiple trips[J]. Journal of Mathematical Modeling and Algorithms,2007,6(4):591-613.

[10]JARBOUI B, DERBEL H S, HANAFI, et al. Variable neighborhood search for location routing[J]. Computers & Operations Research,2013,40(1):47-57.

[11]张晓楠,范厚明,李剑锋.同时配集货定位—路线问题的变邻域分散搜索算法[J].计算机集成制造系统,2015,21(9)：2535-2548.

[12]潘全科,王文宏,朱剑英.基于粒子群优化和变邻域搜索的混合调度算法[J].计算机集成制造系统,2007,13(2):323-328.

[13]戈军,周莲英.面向动态车辆路径的改进变邻域搜索算法[J].计算机工程与应用,2013,49(23):71-74.

Application of Improved Variable Neighborhood Search Algorithm for VRPMT

SONG Qiang1)DU Nuannan2)

(DepartmentofInformationEngineering,GuangdongPolytechnicCollege,Zhaoqing526100,China)1)(SchoolofComputerandSoftwareEngineering,PingdingshanIndustrialCollegeofTechnology,Pingdingshan467001,China)2)

The vehicle routing problem with multiple paths is a variant of the standard VRP, where each vehicle can be used more than once during the working period. For this NP-Hard problem, this paper proposes an improved variable neighborhood search algorithm in which four neighborhood structure are designed to find the planning of paths. The algorithm is tested on a set of benchmark problems and the obtained solutions are compared with five previously proposed algorithms. Encouraging results are obtained.

vehicle routing; multipath; variable neighborhood search; shaking

2016-10-26

*河南省科技攻关基金项目资助(142102210231)

TP301.6

10.3963/j.issn.2095-3844.2017.01.006

宋强(1971—)：男，副教授，博士生，主要研究领域为计算机控制技术与算法优化