基于分层聚类和干扰对齐的MIMO链路调度算法*

熊 最 王可人 金 虎 钱 锋

(电子工程学院通信系，合肥，230037)

基于分层聚类和干扰对齐的MIMO链路调度算法*

熊 最 王可人 金 虎 钱 锋

(电子工程学院通信系，合肥，230037)

为了降低干扰对齐所需的处理开销，将链路划分为多个簇分别进行处理成为可行的办法之一。针对现有簇划分算法中运算复杂度较高的问题，本文提出了一种基于最小信干比的簇划分算法。在此基础上，针对所有簇同时通信造成部分簇内链路接收端信干噪比(Signal to interference plus noise ratio，SINR)较低的问题，本文将以链路为单位的调度问题等效为以簇为单位的调度问题，提出了一种基于层次聚类的簇调度算法。理论与仿真实验结果表明，本文所提出的簇划分算法的运算复杂度明显低于现有算法，且相同条件下的系统平均吞吐量更高。同时，本文提出的基于簇层次聚类的调度算法不同程度地提升了各簇内链路接收端的SINR，系统可根据不同的性能需求进行调度策略选择。

链路调度；干扰对齐；MIMO网络；分层聚类

引 言

无线网络中链路调度问题与反映干扰关系的干扰模型密切相关，选择一种合适的干扰模型为链路调度的实施提供条件显得尤为重要。物理干扰模型的出现，弥补了协议干扰模型的缺陷。在物理干扰模型下，每条链路上的干扰等于网络中所有并行传输链路造成的干扰总和。由于该模型下的链路调度问题已经被证实为NP-hard问题，近些年来，研究者们主要在基于物理干扰模型的分布式调度方案[1-10]上开展研究。文献[11]在MIMO系统中研究了分集增益与复用增益之间的关系。文献[12]在物理干扰模型的基础之上提出了一种MIMO-pipe模型，该模型充分考虑到MIMO网络中给定每个通信节点上的天线数量和传输功率，总结出每条链路上传输的不同数据流越多，其干扰容忍性能越差的结论。MIMO-pipe模型提供给上层的是可行传输速率与信干噪比(Signal to interference plus noise ratio，SINR)需求的对应关系集。文献[13]将MIMO-pipe模型运用到了分布式CSMA链路调度中，但其对链路间干扰的处理并未深入研究。2008年，Syed Jafar提出了一种被称为干扰对齐[14](Interference alignment,IA)的干扰管理方法，其主要思路是通过设计发送和接收的预编码矩阵，将用户所接收到的干扰信号(非期望信号)对齐到一个与期望信号正交的子空间内，从而消除干扰信号对期望信号的干扰。文献[15,16]试图将IA与MIMO-pipe模型相结合用以解决链路调度问题，但其过于局限于理想干扰对齐的场景，忽视了网络中链路位置信息和路径衰落等问题。基于这一现实，Clustered-IA成为解决这一问题的新办法。Clustered-IA的概念最早由Tresch R和Guilaud M提出，并应用在蜂窝网络[17,18]和ad hoc网络[19]中。他们将网络中的链路进行聚类，并划分为不同的簇，针对每个簇独立运用IA进行运算，由此获得了在可行速率和中断概率等性能上的增益。文献[20]考虑了如何降低干扰信道中的用户划分所带来的开销，并分析了划分方法与开销之间的关系。在多用户MIMIO干扰网络中，文献[21]考虑到由于路径衰落的影响网络中部分链路之间的干扰可以忽略，同时全网络中普遍使用IA会导致可行性的不确定性和运算量较大的问题，提出将网络中相互干扰较大的链路调度在同一个簇，而将相互间干扰较小的链路调度在不同的簇。这一思想将网络中的链路划分成了多个由小数量链路组成的簇，一方面保证了IA的可行性，另一方面降低了干扰消除所需的运算开销。但文献[22]假设所有的簇均同时通信，此时每个簇中的MIMO链路都将受到不同程度的簇间干扰，导致链路接收端SINR容易出现过低的情况。因此，为了降低多用户MIMIO干扰网络中簇划分所需的开销，并保证每个簇中的MIMO链路均能达到通信所需的SINR，本文首先提出了一种基于最小信干比的簇划分方法，在获取簇划分方案的基础上，提出了一种基于层次聚类与IA的簇调度算法。

1 系统模型

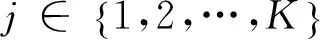
(1)

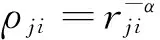
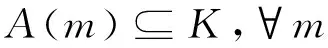
(2)

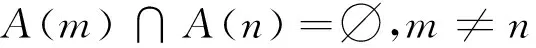
(3)

(4)

令mj表示第j条链路所在的聚类编号，即mj=n，j∈A(n)。因此，对不同干扰源形成的干扰进行聚类，可将其划分为簇内(intra-cluster)干扰和簇间(inter-cluster)干扰。那么，第j个用户接收端其接收信号可表示为

(5)

因此，对应任意用户j所能获得的可达传输速率可表示为

(6)

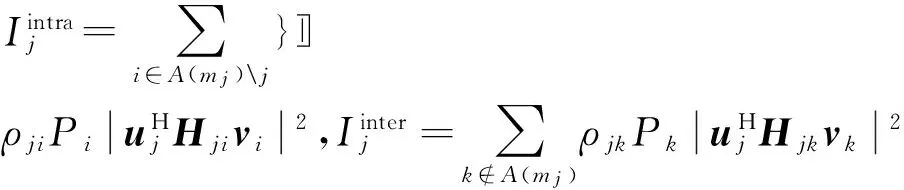
由于基于最大信干噪比(Maximalsignaltointerferenceplusnoiseratio，MaxSINR)准则的干扰对齐算法[22]相比其他准则的干扰对齐算法能够获得更高的期望信号增益，因此，本文选用MaxSINR准则作为干扰对齐的优化目标。从根本上说，MaxSINR准则的干扰对齐算法是一种迭代算法，其每一步都是给定发射端预编码矩阵，由接收端的接收矩阵来完成优化，即使得接收端的SINR最大化,有

(7)

其中

(8)

φk=∑j∉A(mk)ρkjPj表示所有簇间干扰之和，并视为白噪声，可得到接收矩阵的向量，即

(9)

2 基于MinSIR的簇划分算法

文献[21]通过建立以可行速率损失为权重的冲突图G=(V,E,W)，其中，V为图的顶点集合，每个顶点代表无线网络中的一条链路，E为图的边集合，每一条边代表网络中相应两条链路之间的干扰，W为图的权重集合，每个权重值代表网络中相应两条链路之间的干扰程度。并先后提出了两种簇划分方法，一种是对IA可行性做强制性保证，即簇的大小必须保证IA能够消除每个簇内所有链路间的干扰；另一种是不对簇的大小作强制要求，允许簇内干扰不完全消除。文中指出，后者比前者涵盖更多较强的干扰链路，且所获得的可行性和速率相对较高。两种方法均选取每两条链路之间的有效速率损失作为权重，但处理过程都比较复杂。以文献[21]中提出的第2种划分方法为例，在给定簇个数NA的条件下，首先对权重W进行特征值分解，求解对应于前NA个较大特征值的特征向量，然后将求得的特征向量组成一个K×NA为矩阵，最后对该矩阵采用Kmeans算法，从而达到将网络中K条链路划分为NA个簇的目的。为了降低上述簇划分的运算复杂度，本文提出一种基于最小信干比(Minimumsignaltointerferenceratio，MinSIR)的簇划分算法，记为算法1。

对于任意链路i和链路j，当两条链路处于同一簇时，通过干扰对齐的处理，两者之间的干扰可得到消除，而当两条链路处于不同簇时，两者之间会形成干扰。因此，在链路i的接收端，其信干比可表示为

(10)

同理，在链路j的接收端，其信干比可表示为

(11)

因此，定义链路i和链路j之间的权重可表示为

(12)

由式(12)可知，若两条链路之间的信干比之和越小，即可判定它们之间的干扰越大。由此可建立以最小化信干比为目标的优化函数，即有

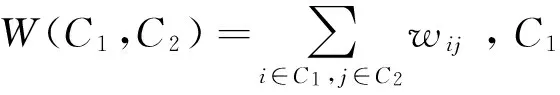
为了求解该优化问题，可直接对权重集合W采用Kmeans算法将网络中的链路进行划分。与文献

表1 本文算法1与文献[21]算法复杂度对比

[21]中的处理过程相比，本文提出的基于MinSIR的簇划分算法省去了求解特征值分解的步骤，降低了簇划分过程的运算复杂度，如表1所示。从表1中给出的对比结果可以看出，当网络中链路数K和簇的个数NA均给定时，本文算法的运算复杂度明显低于文献[21]中的划分算法；当链路数K不断增大时，这种优势更加明显。

3 基于簇的层次聚类算法

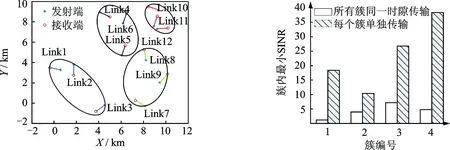
图1 簇划分结果Fig.1 Clustering results图2 簇内最小SINR比较Fig.2 In-cluster SINR comparison of each cluster

在第2节中，网络中的链路根据链路间相互干扰的程度被划分为多个簇，使得相互干扰较严重的链路处于同一簇内，而相互干扰相对较弱的链路则被划分到不同簇。然而，当所有簇同时在同一时隙内传输数据时，簇内链路因受到簇外链路的众多干扰，其接收端的SINR最小，而当每个簇分别在某一时隙传输数据时，即没有簇外链路造成干扰的情况下，簇内链路接收端的SINR相对较大。设链路总数为12，其簇划分结果如图1所示。相比于所有簇同时进行调度的情况，单个簇进行调度时，簇内链路最低SINR明显提高,其结果如图2所示。因此为了提升簇内链路接收端的SINR水平，保证所有簇内链路均达到传输需求，本节考虑将以链路为单位的调度问题转化为以簇为单位的调度问题。

将以簇为单位的无线网络等效为一个带权重的冲突图Gc=(Vc,Ec,Wc)，即将NA个簇分别作为冲突图的顶点，每2个簇的连线视为其可在同一时隙内调度，连线上的权重Wc设置为相邻2个簇由单独传输到并行传输时SINR的损失之和，即

式中：Δij=SINRi-SINRij，Δji=SINRj-SINRji。SINRi表示第i个簇单独在某一时隙内传输时簇内链路接收端的信干噪比之和，SINRij表示第i个簇和第j个簇同时在某一时隙内传输时第i个簇内链路接收端的信干噪比之和，Δij即可反映出第i个簇在单独传输和与第j个簇同时传输时的信干噪比损失。两个不同簇之间的权重越小，说明两者在同一时隙内被调度的可能性越高。因此，为了比较不同调度方案的性能，本文采取层次聚类算法对NA个簇进行划分，将该算法记为算法2，其输入为算法1所得的簇划分结果，输出为多层次簇调度方案。算法2的主要步骤可概括为：(1) 根据算法1中得到的簇划分结果，计算每个簇的簇内干扰Iintra；(2) 计算每两个簇在同一时隙内传输所产生的簇间干扰Iinter；(3) 根据簇内干扰Iintra和簇间干扰Iinter计算相应的SINR损失和传输速率损失，获取权重矩阵Wc；(4) 将权重矩阵Wc视为每个簇在NA维度上的坐标，采用层次聚类对各簇进行不同层次的划分；(5) 获取最终的多层次调度方案。

4 仿真实验

前文中针对MIMO链路的簇划分算法和簇调度算法进行了详细的介绍，本节将对所提算法的相关性能进行仿真。主要进行3轮实验：(1)比较本文所提的算法1与文献[21]算法的簇划分结果对系统吞吐量的影响；(2)比较本文算法2与文献[22]算法的簇内链路SINR水平；(3)比较本文算法2与文献[21]算法的和速率与吞吐量水平。为了便于比较，在3轮实验中，MIMO链路总数K均设为12，每条链路的收发端天线均配置为M=N=2，每条链路的通信距离均设为1km，路径衰减因子为3.76，所处环境中的背景噪声为均值为0，方差为1的高斯白噪声。为了保证实验结果的有效性，每组参数条件下的实验结果均取1 000次重复实验结果的平均值。

实验1 考虑不同发射功率条件下时，本文所提算法1与文献[21]算法的簇划分结果对系统吞吐量的影响。设网络中每条链路发射功率从0dBW到40dBW变化，且所有簇同时在同一时隙内进行调度。仿真结果如图3所示。

实验2 考虑发射功率不同条件下时，比较本文所提算法2与文献[21]算法的簇内链路SINR水平。设网络中每条链路发射功率从0dBW到40dBW变化，且所有划分后的簇均按照不同时隙数分别进行调度。仿真结果如图4所示。

实验3 考虑发射功率不同条件下时，比较本文所提算法2与文献[21]算法的和速率性能与吞吐量性能。设网络中每条链路发射功率为0dBW到40dBW变化，且所有簇按照不同时隙数分别进行调度。仿真结果如图5，6所示。

从图3中的仿真结果可以看出，当发射功率低于10dBW时，本文簇划分算法与文献[21]中的算法所获得的吞吐量性能十分接近，而当每条链路发射功率高于10dBW时，本文提出的簇划分算法所获得的系统吞吐量性能明显好于文献[21]。这说明在发射功率较高时，相比于文献[21]中的算法，本文算法

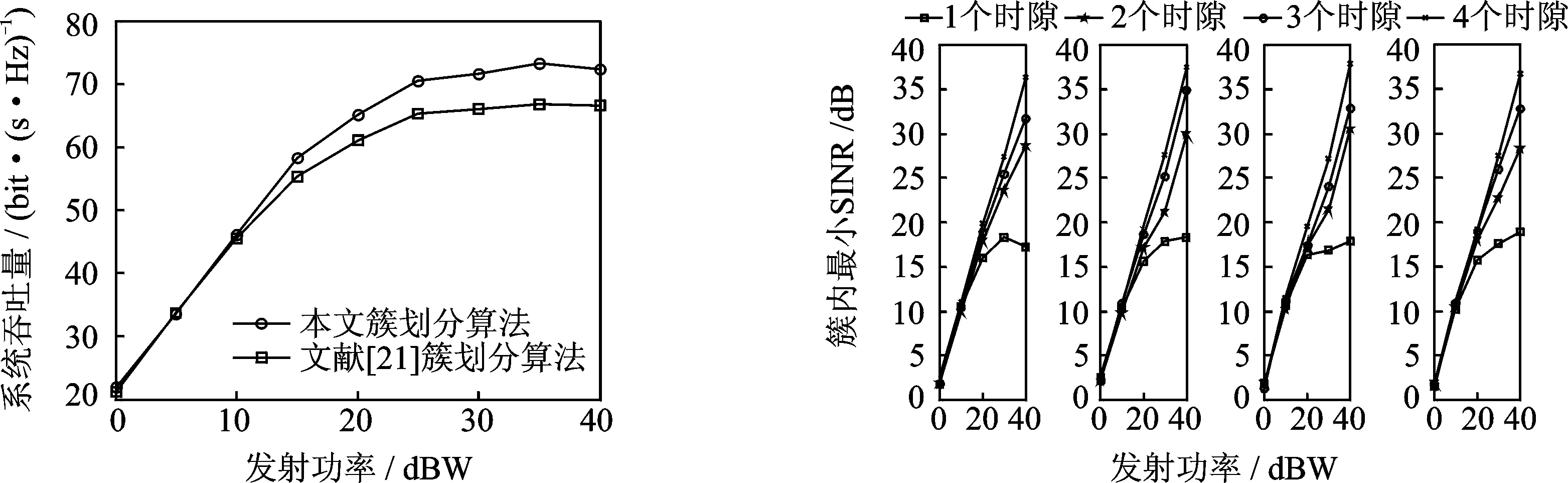
图3 簇划分算法对系统吞吐量性能的影响

Fig.3Effectivenessofclusteringonthesystemthroughput

图4 不同调度时隙下簇内最小SINR变化

Fig.4In-clusterminimumSINRwithdifferenttimeslots

图5 不同调度时隙数下和速率对比Fig.5 Sum rate comparison with different timeslots图6 不同调度时隙数下系统吞吐量对比Fig.6 Throughput comparison with different timeslots

能够有效提升簇内链路接收端的SINR水平，从而获取较高的传输速率。

从图4中的仿真结果对比可以看出，当发射功率增加时，不同调度时隙下簇内最小SINR均不同程度提高。但随着发射功率的不断提高，簇间干扰随之增大，单个时隙调度所获取的簇内链路SINR水平明显处于劣势，且差距越来越明显。正是图4中给出的SINR水平的变化，造成在不同时隙数调度方案下，系统所获得的和速率性能发生了明显变化。如图5所示，当采取多个时隙进行簇调度时，时隙数增加，系统所获得的和速率性能更好。与此同时，通过图6给出的仿真结果可以看出，尽管本文提出的多层次调度算法获得了较好的和速率性能，但由于调度时隙数的增加，系统总的平均吞吐量有一定降低。

5 结束语

为了降低干扰对齐在获取全局信道状态信息时产生的开销，本文试图将链路划分为多个簇分别进行干扰对齐处理。针对现有簇划分算法中运算复杂度较高的问题，本文提出了一种基于最小信干比的簇划分算法，将相互间干扰较大的链路划分到同一簇内。在此基础上，针对所有簇同时通信造成部分簇内链路接收端SINR较低的问题，本文将以链路为单位的调度问题等效为以簇为单位的调度问题，并采用层次聚类的方式实现簇调度算法。理论分析和实验仿真，结果表明本文所提的算法达到了预期目的。但仍然存在有待解决的问题，一方面是干扰对齐在MIMO链路调度中的应用价值仍只显现出冰山一角，仍有诸如降低CSI依赖、对信道估计误差的鲁棒性等更多有价值的内容值得进一步研究；另一方面，在运用干扰对齐的同时，仍需要进一步探索有效提升系统吞吐量的办法。

[1]WanPengjun,JiaXiaohua,YaoF.Maximumindependentsetoflinksunderphysicalinterferencemodel[C]∥2009InternationalConferenceonWirelessAlgorithms,SystemsandApplications.Boston,MA,USA:Springer, 2009: 169-178.

[2]XuX,TangS,PengJunWan.Maximumweightedindependentsetoflinksunderphysicalinterferencemodel[C]∥2010InternationalConferenceonWirelessAlgorithms,SystemsandApplications.Beijing,China:Springer, 2010: 68-74.

[3]LongBaole,ModianoE,JooC,etal.LongestqueuefirstschedulingunderSINRinterferencemodel[C]∥11thACMInternationalSymbosiumonMobileAdHocNetworkingandComputing.NewYork,USA:ACM, 2010: 41-50.

[4]KompellaS,WieselthierJE,EphremidesA,etal.OnoptimalSINR-basedschedulinginmulti-hopwirelessnetworks[J].IEEE/ACMTransactionsonNetworking, 2010, 18 (6): 1713-1724.

[5]WanPengjun,FriederO,JiaXiaohua,etal.Wirelesslinkschedulingunderphysicalinterferencemodel[C]∥30thIEEEInternationalConferenceonComputerCommunications.Shanghai,China:IEEE, 2011: 838-845.

[6] 樊帅, 张林, 冯伟,等. 基于物理干扰模型的分布式传输调度算法[J]. 清华大学学报:自然科学版, 2011, 51(11): 1631-1636.

FanShuai,ZhangLin,FengWei,etal.Distributedlinkschedulingalgorithmwithaphysicalinterferencemodel[J].JournalofTsinghuaUniversity:ScienceandTechnology, 2011, 51(11): 1631-1636.

[7]SuJinzhao,CaoJing,WuWei.Grayphysicalinterferencemodelbasedlinkschedulingalgorithm[J].ScienceChina(InformationScience), 2012, 55(6): 1337-1350.

[8]RyuJ,JooC,KwonTT,etal.DSS:DistributedSINR-basedschedulingalgorithmformulti-hopwirelessnetworks[J].IEEETransactionsonMobileComputing, 2013, 12 (6): 1120-1132.

[9]DongSha,YangQinghai,FuFenglin,etal.Distributedlinkschedulingforcongestioncontrolinmulti-hopwirelessnetwork[C]∥IEEEInternationalConferenceonWirelessCommunications&SignalProcessing.Hangzhou,China:IEEE,2013: 1-5.

[10]ZhouYaqin,LiXiangyang,LiuMin,etal.Throughputoptimizinglocalizedlinkschedulingformulti-hopwirelessnetworksunderphysicalinterferencemodel[J].IEEETransactionsonParallelandDistributedSystem, 2013, 25(10): 2708-2720.

[11]黄丘林, 史小卫.MIMO系统中分集增益和空间复用增益的折衷关系 [J]. 电子与信息学报, 2007, 29 (3): 681-685.

HuangQiulin,ShiXiaowei.Trade-offbetweendiversitygainandmultiplexinggaininMIMOsystems[J].JournalofElectronics&InformationTechnology, 2007, 29 (3): 681-685.

[12]GeWeiyan,ZhangJunshan,XueGuoliang.MIMO-pipemodelingandschedulingforefficientinterferencemanagementinmulti-hopMIMOnetworks[J].IEEETransactionsonVehicularTechnology, 2010, 59 (8): 3966-3978.

[13]QianDajun,ZhengDong,ZhangJunshan,etal.DistributedCSMAalgorithmsforlinkschedulinginmulti-hopMIMOnetworksunderSINRmodel[C]∥29thIEEEInternationalConferenceonComputerCommunications.SanDiego,CA:IEEE, 2010: 1-14.

[14]CadambeVR,JafarSA.Interferencealignmentandthedegreesoffreedomofthekuserinterferencechannel[J].IEEETransactionsonInformationTheory. 2008, 54 (8): 3425-3441.

[15]AoXin,YuFR,JiangShengming,etal.Onthroughputgainofinterferencealignmentinmulti-hopMIMOnetworks[C]∥IEEEInternationalConferenceonCommunications.Sydney,NSW:IEEE, 2014: 59-64.

[16]敖欣. 基于干扰管理的无线自组织网性能优化研究[D]. 广州：华南理工大学，2012.

AoXin.Performanceoptimizationforwirelessadhocnetworksbasedoninterferencemanagement[D].Guangzhou:SouthChinaUniversityofTechnology, 2012.

[17]TreschR,GuillaudM.Clusteredinterferencealignmentinlargecellularnetworks[C]∥IEEEInternationalSymposiumonPersonal.IndoorandMobileRadioCommunications,Tokyo,Japan:IEEE, 2009: 1024-1028.

[18]TreschR,GuillaudM.Performanceofinterferencealignmentinclusteredwirelessadhocnetworks[C]∥IEEEInternationalSymposiumonInformationTheory.Austin,TX:IEEE, 2010: 1703-1707.

[19]TreschR,AlfanoG,GuillaudM.Interferencealignmentinclusteredadhocnetworks:Highreliabilityregimeandper-clusteraloha[C]∥IEEEInternationalConferenceonAcoustics,SpeechandSignalProcessing(ICASSP).Prague,CzechRepublic:IEEE, 2011: 3348-3351.

[20]PetersSW,HeathJRW.UserpartitioningforlessoverheadinMIMOinterferencechannels[J].IEEETransactionsonWirelessCommunications, 2012, 11 (2): 592-603.

[21]ChenSujie,ChengRS.Clusteringforinterferencealignmentinmultiuserinterferencenetwork[J].IEEETransactionsonVehicularTechnology, 2014, 63 (6): 2613-2624.

[22]GomadamK,CadambeVR,JafarSA.Approachingthecapacityofwirelessnetworksthroughdistributedinterferencealignment[J].IEEETransactionsonInformationTheory, 2011, 57 (6): 3309-3322.

Novel MIMO Link Scheduling Algorithm Based on Hierarchical Clustering and Interference Alignment

Xiong Zui, Wang Keren, Jin Hu, Qian Feng

(Department of Communications, Electronic Engineering Institute, Hefei, 230037, China)

The signaling overheads of interference alignment (IA) obtaining global channel state information increase with the number of links. Grouping the links into clusters, within which the interference are processed by IA, becomes an effective method to reduce the overheads. Considering the fact of high computational complexity in the process of link partition, an alternative link partition algorithm based on minimum signal-to-interference-ratio (MinSIR) is proposed. Furthermore, when all the clusters simultaneously transmit in a single timeslot, the signal-to interference-plus-noise-ratio (SINR) at the receivers of several links was insufficient for successful transmission. To solve such a problem, the link scheduling problem was substituted by a novel cluster-based scheduling algorithm using hierarchical clustering. The theoretical analysis and simulation results show that the proposed link partition algorithm obviously reduced the computational complexity, and obtained superiors system throughput. Meanwhile, the cluster-based scheduling algorithm effectively improved the SINR at the receivers of links, which potentially supported the system decision of scheduling scheme for specified performance demand.

MIMO network; interference alignment; MIMO network; hierarchical clustering

2015-04-01；

2016-02-23

TN914

A

熊最(1988-)，男，博士研究生，研究方向：通信信号处理、干扰对齐，E-mail：lidaysue@126.com。

钱锋(1981-)，男，博士，讲师，研究方向:通信信号处理、混沌信号处理。

王可人(1957-)，男，教授，博士生导师，研究方向：通信信号处理。

金虎(1974-)，男，博士，副教授，研究方向：通信信号处理、混沌信号处理。