基于核稀疏保持投影的典型相关分析算法*

张 荣 孙权森

(南京理工大学计算机科学与工程学院，南京，210094)

基于核稀疏保持投影的典型相关分析算法*

张 荣 孙权森

(南京理工大学计算机科学与工程学院，南京，210094)

模式识别的技术核心就是特征提取，而特征融合则是对特征提取方法的强力补充，对于提高特征的识别效率具有重要作用。本文基于稀疏表示方法，将稀疏表示方法用到高维度空间，并利用核方法在高维度空间进行稀疏表示，用其计算核稀疏表示系数，同时研究了核稀疏保持投影算法(Kernel sparsity preserve projection,KSPP)。将KSPP引入到典型相关分析算法(Canonical correlation analysis,CCA)，研究了基于核稀疏保持投影的典型相关分析算法(Kernel sparsity preserve canonical correlation analysis,K-SPCCA)。在多特征手写体数据库和人脸图像数据库上分别证实了本文提出方法的可靠性和有效性。

特征提取;核稀疏表示;核稀疏保持投影;典型相关分析

引 言

随着压缩感知理论的迅速发展，在20世纪90年代，稀疏表示理论应运而生，稀疏表示理论就是从原始的高维样本数据中提取低维空间的特征，使得这个投影满足稀疏性，使得这个表示系数的非0个数最少。通常使用过完备字典[1]的设计来求解稀疏表示系数，其原理是：字典中的所有元素选取全部的原始高维样本数据，然后在字典中尽量选择最少的基本元素来表示原始高维的样本数据，从而使这个表示系数里不是0的个数越少越好。Qiao[2]等提出了一种基于稀疏表示的特征提取的方法——稀疏保持投影(Sparsity preserve projection,SPP)，而最近侯书东等[3,4]受稀疏算法的启发，将SPP引入到典型相关分析(Canonical correlation analysis,CCA)中，提出了基于稀疏保持的典型相关分析(Sparsity preserve canonical correlation analysis， SPCCA)，这种算法不仅约束了样本之间的稀疏重构性，同时实现了两组不同特征之间的特征融合，从而增强了该特征提取方法的识别率。Sun通过原始样本数据提取两种不同的特征，以这两组不同的特征作为典型相关分析的两组输入数据，在CCA准则下最大化这两组特征的相关性，得到两组投影矢量，通过不同的策略，融合这两组投影矢量，对原始样本数据进行新特征提取工作，用于样本数据的分类。CCA是一种线性的特征提取模型，其计算能力有限。一般而言，现实世界中很多复杂的应用问题，比如Shen[5]等提出了正交化CCA，还有核的CCA[6]都是比线性函数更富有表达能力的假设空间。核方法的原理是：通过某种未知的非线性映射关系，将原始样本数据映射到高维特征空间或者无穷维的特征空间，然后在新的空间中进行线性形式的操作。尽管通过这种非线性的映射，存在以下问题：非线性映射函数形式的不确定和函数的某些参数不确定等，但是这些问题都可以通过核函数技术的内积运算加以解决。20世纪90年代以来，随着核方法在支持向量机(SVM)[7,8]中的成功应用，一大批核化的算法相继被提出，核技术在模式识别领域得到了很大扩展和成功运用，主要包括两方面：新方法主要用于支持向量机中，但是这里使得SVM结构风险最小；传统方法改造提出了很多有效地稳定的算法，主要包括核主元分析(Kernel PCA，KPCA)[9]、核主元回归(Kernel PCR，KPCR)、核部分最小二乘法(Kernel PLS，KPLS)、核Fisher判别分析(Kernel fisher discriminator，KFD)[10,11]以及核独立主元分析(Kernel independent component analysis，KICA)，这些不同的方法在模式识别中都取得了不错的、甚至意想不到的结果。这些核方法在处理非线性问题时都获得了成功。根据Cover T的模式可分性定理，当模式分类问题映射到高维空间时，会比在低维度空间更加容易可识别或者说可分[12]。受该定理的启发，本文运用核方法(所谓“核技巧”[8,13]，就是在算法中出现样本内积时进行核函数代入)，将线性的SPCCA推广到高维特征空间，提出了核化的SPCCA(Kernelized SPCCA，KSPCCA)。最后利用优化策略将它们引入CCA理论。

1 核稀疏保持投影的典型相关分析

1.1 稀疏表示理论[14]

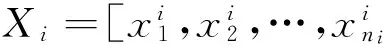
(1)

(2)

所以如果测试样本的类别不知道，就通过所有的原始样本数据的线性组合，表示测试样本y，即

(3)

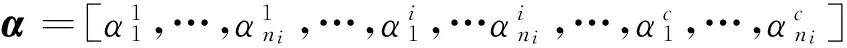
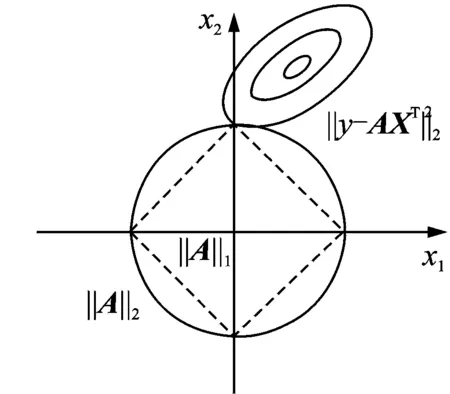
图1 稀疏表示的求解示意图Fig.1 Schematic diagram of solving sparse representation

当式(3)中字典X的基本元素较多时，即原始样本数据很多，系数向量α就会只包含很少数的有用的系数，其他的大部分系数都为0，因而稀疏表示的最后就是要求出解稀疏系数向量α，满足式(3)的解中选择α最稀疏的解，也就是求解式(4)的约束条件的最小化问题，这里采用L1范数来加以限制

(4)

式(4)可以变为下面的正则化表现形式

(5)

图1给出了只有两组特征变量情况下在L1范数和L2范数限制下的优化问题求解图示，图1中正方形虚线表示L1范数的优化，圆形实线表示L2范数的优化，从图中可以很容易地看出，只有范数才能达到稀疏的目的。

1.2 稀疏保持投影算法

SPP算法较好地保持了全局样本间的稀疏重构性。文献[4]中给出了SPP算法的优化目标函数，通过数学推导可得到广义本征方程。

(6)

(7)

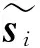
(8)

通过数学推导，可以将式(8)化简为

其中ei表示第i个元素为1，其他均为0的列向量。在求解过程中为了避免出现退化的解，给定约束条件，wTXXTw=1，因此，最终SPP的广义本征方程为

(9)

求解式(9)，取得d个最大特征值所对应的投影向量wi(i=1,…,d)，即为所求的投影。

由于矩阵XXT一般都不可逆，因而式(9)一般不能直接求解，即常说的小样本问题。为了解决小样本问题，就要求在特征提取前对原始样本数据进行PCA操作，降低原始样本数据的特征维数，从而避免XXT奇异。

1.3 核稀疏保持投影

通过核方法将原始的样本数据映射到高维特征空间，改变了原始样本的分布情况，从而将原始样本数据中的非线性问题转化为线性问题。因此，在高维特征空间中，针对新分布的样本情况进行稀疏表示的工作，就可以得到高维特征空间的核稀疏表示系数；利用得到的核稀疏表示系数，构造高维特征空间中样本数据的邻接矩阵来提取数据特征，称为核稀疏保持投影(KSPP)。

1.3.1 核稀疏表示

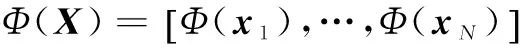
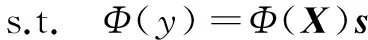
(10)

由于Φ(X)和Φ(xi)均未知，所以式(10)不能直接求解。在约束条件的两边同时乘上Φ(X)T，即

(11)

在高维特征空间中的内积，同样也是通过核函数来求得，两个样本数据x1，x2，映射到高维特征空间后的内积形式为：Φ(x1)TΦ(x2)=K(x1,x2)，则

(12)

并且

(13)

当核函数K(x1,x2)给定时，Φ(X)TΦ(X)和Φ(X)TΦ(y)就可以根据式(12，13)求得，从而求解(11)的最优化问题。

1.3.2 核稀疏保持投影

利用上一小节得到的高维特征空间中的核稀疏表示系数，建立样本数据的邻接矩阵，并用于特征提取工作。同样地，通过某种未知的非线性映射φ，将原始的样本数据xi∈Rp(i=1,…,N)映射到高维特征空间，得到映射后的样本数据φ(xi)(i=1,…,N)。对于现在的高维特征空间任一个样本数据φ(xi)(i=1,…,N)；也同样地，在高维特征空间中用除自己以外的所有样本数据求解自己的稀疏表示系数。其中p表示样本的特征维数，N表示训练样本数，则φ(X)=[φ(x1),…,φ(xN)]表示所有高维特征空间的样本数据。仿照SPP理论的方法， 可以得到KSPP的优化问题模型,即

(14)

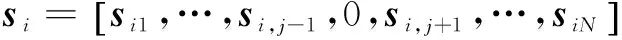
(15)

利用核函数计算高维空间数据的内积，可得

(16)

和

(17)

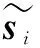
(18)

通过类似SPP的推导，可以得到

同样地，给定约束条件wTΦ(X)Φ(X)Tw=1，这样优化准则可以变成

(19)

等价于最大化准则

(20)

最大化准则可以转化为求解广义本征方程

(21)

w可以表示为

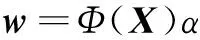
(22)

将式(22)代入式(21)，得到

(23)

式(23)等价于

(24)

从而，广义本征方程可以化简为

(25)

求解式(25)，取得d个最大特征值所对应的投影向量αi(i=1,…,d)。为了归一化KSPP的投影向量wi=Φ(X)αi(i=1,…,d)，就要使得

(26)

则

(27)

高维特征空间样本Φ(x)，经过KSPP投影后的第i个新特征为

(28)

综上所述，KSPP算法可归纳为如下步骤：

(2) 求解广义本征方程(25)对应的前d个最大本征值所对应的本征向量αi(i=1,…,d)。

1.4 核稀疏保持典型相关分析(KSPCCA)

典型相关分析(CCA)[6]的优化准则函数为

(29)

式中：Sxx,Syy分别表示x,y两组随机变量组内的协方差矩阵，Sxy表示x,y两组随机变量之间协方差矩阵，则CCA可表述为如下优化问题的解，即

(30)

(31)

则目标函数可改为

(32)

相应地，由CCA的约束条件可得KSPCCA的约束条件αTKx(I-RT-R+RTR)Kxα=1，βTKy(I-ST-S+STS)Kyβ=1，因此，KSPCCA的约束优化问题可表示为

(33)

利用Lagrange乘子法，不难得到如下关于α,β的广义本征特征值问题

(34)

因此只需利用式(34)，即可求解得α,β，之后取d个最大特征值所对应的特征向量αi(i=1,…,d)和βi(i=1,…,d)。KSPCCA算法可归纳为如下步骤

(2) 求解广义本征方程(34)对应的前d个最大特征值所对应的特征向量αi(i=1,…,d)和βi(i=1,…,d)。

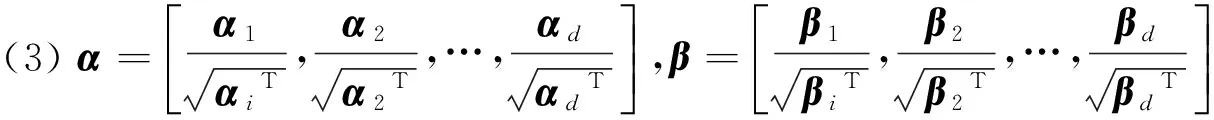
(35)

2 实验与分析

2.1 手写体识别实验

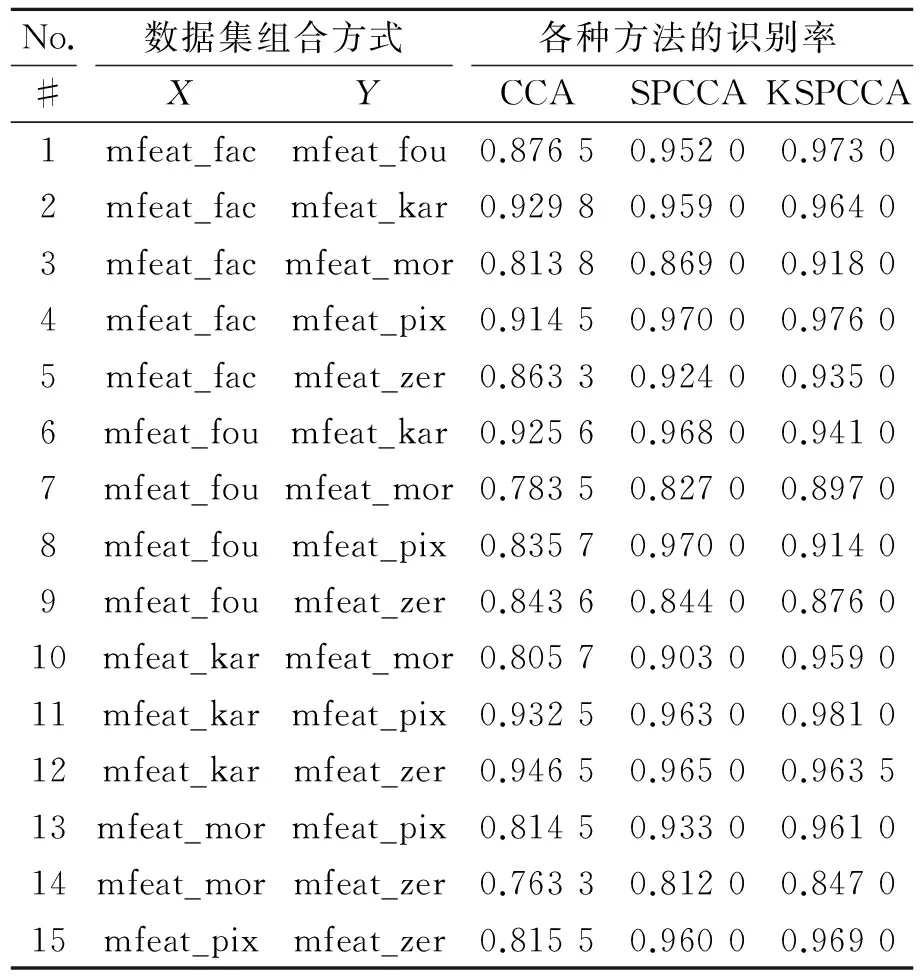
本实验采用多特征手写体数据库(Multiple feature database)，该数据库总共包括0～910个数字手写体，总共包括6组不同的特征，每类200个样本，共2 000个样本。在实验中，对于每种特征组合，在每类数字手写体中随机选取100个样本数字作为训练样本，余下的100个样本作为测试样本，独立随机10次实验，这样的随机试验独立进行10次，记录其平均识别率。实验中，对于KSPCCA中的核函数，选取了高斯核K(x,y)=exp(-‖x-y‖2/t)。这里选取的数据库的特征维数是10，从而作为高斯核的参数t，即t=10。将KSPCCA与CCA[6],SPCCA[14]等算法做对比，其结果如表1所示。

实验结果表明，在不同的数据组合实验中，共有13次组合方式的识别率KSPCCA优于SPCCA和CCA；相反，SPCCA只有2次表现最优。这说明在多数情况下，KSPCCA的识别能力优于SPCCA和CCA，同时，也说明核方法对于线性学习器的性能具有一定的提升作用。

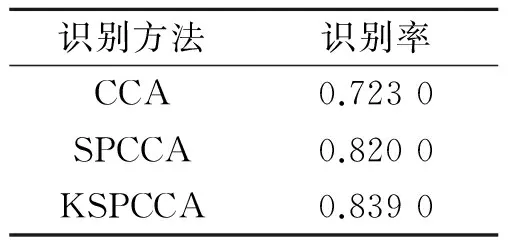
表2 Yale数据集上的识别率

Tab．2 Rate of recognition on data set of Yale face

识别方法识别率CCA0.7230SPCCA0.8200KSPCCA0.8390

2.2 人脸识别实验

为了进一步验证KSPCCA的识别性能， 在Yale人脸数据库上进行人脸识别实验。Yale人脸库数据集主要反映了人脸的表情、光照的不同，该数据库总共包含有15个人，每个人有11幅灰度，在每人11幅图像中选取6幅作训练样本，其余5幅作测试，这样训练集的样本数为90，测试集样本数为75。表2列出了CCA，SPCCA和KSPCCA 3种方法在Yale数据集上的识别率。从实验结果来看，稀疏表示的方法明显增加了人脸识别的性能，大大提高了人脸识别率；然而核方法的加入，虽然识别率有所提高，但是没有明显的提升，这就说明选取核与核参数是一个值得深入探讨的问题，即如何根据样本集的复杂程度(如样本容量、特征维数以及类别数等)并结合数据集的先验知识(如人脸的表情、光照等)启发式地选取合适的核与核参数，如果采用不适当的核反而会造成过拟合而导致识别率下降。

3 结束语

本文中的KSPCCA的实验采用的是高斯核函数，实际上也可以使用其他形式的核函数，如多项式核、Sigmoid核等，核与核参数的选取是数据依赖的，与样本集的复杂度以及数据集的先验知识有关。尽管已经有很多这方面的探索，然而目前核与核参数的选取仍然是一个悬而未决的问题，因此还需进一步思考和探索。

[1] Wright J, Yang A Y, Ganesh A,et al. Robust face recognition via sparse representation[J]. IEEE Transaction on Pattern Analysis and Machine Intelligence, 2009,31(2),210-227.

[2] Qiao L S, Chen S C,Tan X Y.Sparsity preserving projections with application to face recognition[J]. Pattern Recognition,2010,43(1):331-341.

[3] 侯书东,孙权森.稀疏保持典型相关分析及在特征融合中的应用[J].自动化学报,2012,38(4):659-665.

Hou Shudong,Sun Quansen. Sparsity preserving canonical correlation analysis with application in feature fusion[J].Acta Automatica Sinica,2012,38(4):659-665.

[4] 侯书东.基于相关投影分析的特征提取研究及在图像识别中的应用[D].南京:南京理工大学,2012.

Hou Shudong.Feature extraction based on correlation projection analysis and its application to image recognition[D].Nanjing:Nanjing University of Science and Technology,2012.

[5] Shen Xiaobo, Sun Quansen, Yuan Yunhao. Orthogonal canonical correlation analysis and its application in feature fusion[M]. Information Fusion (FUSION), 2013 16th International Conference on.[S.l.]:IEEE, 2013.

[6] Melzer T, Reiter M, Bischof H. Appearance models based on kernel canonical correlation analysis[J]． Pattern Recognition, 2003,36(9):1961-1971.

[7] Mairal J, Bach F, Ponce J, et al. Discriminative learned dictionaries for local image analysis[J].Proceedings of IEEE CVPR, 2008,413(2):1-8.

[8] Mairal J, Bach F, Ponce J, et al. Supervised dictionary learning[J].Proceddings of NIPS. 2009,21:1033-1040.

[9] Scholkopf B, Smola A, Muller K-R. Nonlinear component analysis as a kernel eigenvalue problem[J]． Neural Computation, 1998,10,1299-1319.

[10]Mika S, Ratsch G, Weston J, et al. Fisher discriminant analysis with kernels[J].IEEE Neural Networks for Signal Processing Workshop． 1999,9:41-48.

[11]Baudat G, Anouar F. Generalized discriminant analysis using a kernel approach[J].Neural Computation,2000, 12(10):2385-2404.

[12]Cover T M. Geometrical and statistical properties of systems of linear inequalities with applications in pattern recognition[J]. IEEE Transactions on Electronic Computers, 1965, 14:326-334.

[13]Schölkopf B, Smola A, Müller K-R. Nonlinear component analysis as a kernel eigenvalue problem[J].Neural Computation, 1998, 10, 1299-1319.

[14]侯彬.基于稀疏表示的典型相关分析算法研究[D].南京:南京理工大学,2013.

Hou bin. Canonical correlation analysis algorithm based on sparse representation[D].Nanjing:Nanjing University of Science and Technology,2013.

Canonical Correlation Analysis Algorithm Based on Kernel Sparsity Preserve Projection

Zhang Rong, Sun Quansen

(School of Computer Science and Engineering,Nanjing University of Science & Technology, Nanjing, 210094, China)

The key of pattern recognition is feature extraction. Fusion of feature is an important complement of feature extraction, and it has been proved to be important to improve discrimination. Here, the sparse representation method is studied by introducing sparse representation into a high dimensional feature space and utilizing kernel trick to make sparse representation in the space.The kernel sparse representation coefficients with kernel sparse representation are utilized, then kernel sparsity preserve projection (KSPP) subspace. Moreover KSPP is brought into canonical correlation analysis (CCA), then kernel sparsity preserve canonical correlation analysis (KSPCCA) is studied. The proposed algorithm is reliable and validated on the multiple feature database and face database.

feature extraction; kernel sparse representation; kernel sparsity preserve projection (KSPP); canonical correlation analysis (CCA)

国家自然科学基金(61273251)资助项目。

2014-09-02；

2015-01-13

TP751

A

张荣(1989-)，男，硕士研究生，研究方向：图像处理与识别，E-mail: 15850564451@126.com。

孙权森(1963-)，男，教授，研究方向：模式识别理论与应用、遥感信息系统理论与应用、图形图像技术与应用、多媒体信息处理技术以及医学影像处理与分析。