频率选择性衰落信道下的同步参数联合盲估计算法*

吴天琳 彭 华 黄艳艳

(解放军信息工程大学信息系统工程学院，郑州，450002)

频率选择性衰落信道下的同步参数联合盲估计算法*

吴天琳 彭 华 黄艳艳

(解放军信息工程大学信息系统工程学院，郑州，450002)

对于多径频率选择性衰落信道以及低信噪比环境下线性调制信号的同步参数盲估计问题，提出基于循环累积量的载波频偏、初始相偏和符号定时误差前向联合盲估计算法。通过理论推导得出多径频率选择性衰落信道下信号的循环累积量与初始相偏和符号定时误差的数学关系。在此基础上先以较大频率间隔进行粗估计确定频偏范围，再以较高精度遍历检测信号特定循环频率，提高载波频偏估计精度，进而由累积量值估计出初始相偏和符号定时误差，不依赖于信道衰落和加性噪声的分布特性，尤其适用于频偏、相偏、定时误差和信道衰落同时存在的复杂情况。仿真结果表明，该算法能有效实现低信噪比和多径频率选择性衰落信道下对线性调制信号同步参数的联合盲估计。

多径频率选择性衰落；低信噪比；同步参数；盲估计；循环累积量

引 言

数字通信信号在传输过程中由于信道的影响、多普勒效应和收发端晶振频率不匹配等原因导致接收端载波频率、初始相位的偏移和符号定时误差。自适应反馈环常被用于跟踪和补偿上述偏移和误差，虽然具有较高的精度，但因收敛速度慢、捕获范围小，因此在高速或突发通信时，闭环方法在跟踪偏差之前仍需要依靠基于训练序列的开环前向估计器进行捕获[1]。基于最大似然的前向估计方法计算复杂度低、精度高，但在去除符号信息时引入自噪声，将严重影响算法估计性能[2]，文献[3]通过采用预滤波和后滤波来减小自噪声对同步性能的影响。另外，衰落信道和低信噪比时信号失真严重，实现准确的同步参数盲估计难度更大。文献[4]提出了时间-频率选择性衰落信道下非数据辅助的载波同步开环算法，但需要已完成定时同步为前提。由于数字通信信号的循环平稳特性，循环累积量成为了数字通信信号分析的有效手段之一。理想状态下，高阶循环累积量可抑制平稳噪声和非平稳高斯噪声，从而提高信噪比；另外，由于无需进行去调制处理，避免了去除符号信息时引入的自噪声，从而有利于信号的参数估计。文献[5]通过线性调制信号二阶循环统计量对定时误差实现了盲估计，本质上隐含地把最大似然(Maximum likelihood,ML)应用于信号的二阶统计量，估计性能接近克拉美罗界，但未考虑多径信道和存在频偏和相偏的情况。文献[6]将基于二阶循环统计量的方法扩展到频率选择性多径信道中，实现了载波频偏和符号定时误差的联合估计，但达到较准确估计所需数据量大，不适宜实时处理。文献[7]研究了一种循环频率的检测方法，通过检测信号的循环统计量实现信号频偏的盲估计，在低信噪比和衰落信道下性能良好，但受制于高复杂度，频偏估计精度较低。以上文献均没有考虑载波初始相偏的估计。文献[8]针对多进制数字相位调制(Multiple phase shift keying, MPSK)信号提出了一种基于最小二乘的相位估计算法，具有稳定性高且复杂度低的优点，但要求高斯白噪声信道。

在同时存在频偏、相偏以及定时误差的情况下，目前对单一参数的估计算法性能降低甚至失效[9]。本文针对线性调制信号在频率选择性衰落信道环境下的载波以及符号盲同步问题，建立了多径信道下信号的四阶循环累积量模型，利用其仅在特定循环频率处不为零的特点，先以较大频率间隔遍历循环频率进行粗估计，再减小频率间隔，利用循环频率检测方法提取出高精度的载波频偏信息，在此基础上通过计算两个与4倍载波频偏有关的循环频率处的循环累积量，提取出初始相位偏移和符号定时误差信息，从而对多径衰落信道环境下信号的载波频偏、相偏及定时误差实现了联合盲估计。该算法在低信噪比的频率选择性衰落信道下对3种参数进行了联合估计,避免了已有算法进行单个参数分别估计的局限性，对不同种类和阶数的调制方式有较强的鲁棒性。

1 信号模型

(1)

设多径衰落信道复低通冲击响应为

(2)

式中：m为多径数；ai(t)为单位冲激函数；δ(·)为第i径分量幅度衰落；τi(t)为第i径分量时延。假定信道衰落慢于信号变化，则各径衰减系数和时延设为常数ai和τi，发送信号经线性调制并通过信道到达接收端时，基带复包络为

(3)

待估参数有：收发端载波频率偏移fe、符号定时误差ε(εT为符号周期内传输延时，0≤ε<1 ) 、初始相位偏移θ。w(t)为复加性噪声。r(t)通过匹配滤波器grec(t) 后，以采样率P/T过采样得到离散时间序列

(4)

式中：w(n)=w(t)*grec(t)|t=nT/P；gi(n)=gc(t-εT-τi)|t=nT/P；gc(t)=gtr(t)*grec(t)。从式(4)看出，受到多径信道的影响(m>1)，接收端产生码间干扰，从而造成信号失真，增大了对频偏、相偏和定时误差估计的难度。

2 频率相位偏移和定时误差的联合盲估计算法

2.1 循环累积量相关理论

一个复循环平稳过程r(t)的n阶q次时变累积量可表示成关于时间的周期函数cr(t,τ)n,q，它的傅里叶级数系数即为其n阶q次共轭循环累积量cr(α,τ)n,q

(5)

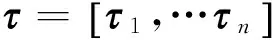
(6)

式中：T为符号周期；a为幅度衰减因子；(-)p,p=1,…,n表示第p个延时可能取负，取负操作总共为q次；cw(α,τ)n,q为噪声的循环累积量，当n≥2时其理论值为0；α为循环频率，取值与符号周期和频偏fe有关。循环频率域是

(7)

2.2 频率选择性衰落信道下频率、相位偏移和符号定时误差估计

通过循环累积量估计单载波线性数字(Singlecarrierlineardigital,SCLD)信号频率偏移需要满足以下条件

(8)

对于星座对称的信号，n为奇数时累积量为0[10]，对于多进制正交幅度调制(Multiplequadratureamplitudemodulation,MQAM) (M>4)，cMQAM,2,0=cMQAM,4,1=0，考虑常用的MPSK和MQAM信号，本文选取四阶循环累积量进行参数估计。由式(4)和式(6)可知，第i径信号四阶循环累积量为

(9)

延迟大于一个符号周期的信号与原信号近似独立，且各路径传输函数相互独立，因此式(4)中多径接收信号也可认为近似独立。由式(4)和式(9)以及累积量的性质[11]可得多径信道下信号的循环累积量为

(10)

循环频率集为

(11)

2.2.1 频偏估计及精度分析

由式(11)可知，信号四阶循环累积量的循环频率里包含频偏信息。令β=0，此时循环频率对应值为

(12)

选择感兴趣的频率区间为循环频率的检测范围，只需检测出范围内的频率值，即得到频偏估计值。实际进行计算时，cr(α,0)4,0的估计值可从有限个样本的n阶时变矩得到。

假设信号样本x(n)的k阶循环矩数值为

(13)

根据矩-累积量转换公式，并将式(4)代入，令τ1=τ2=τ3=0可得信号的四阶循环累积量估计值为

(14)

式中：〈·(n)〉n表示对以n为变量的样本取平均值。

从理论上看，循环累积量在循环频率域外的频率分量上值为0，但因为实际计算时，只采用有限样本利用式(14)估计cr(α,0)4,0，在循环频率外的频率上循环累积量并不为0。常见做法是以检测感兴趣范围内的使得循环累积量估计值为最大的频率为循环频率的估计值。但在恶劣信道环境中，且要求频率估计精度较高的情况下，循环累积量在循环频率真值的附近取值可能会出现与真值处相差很小甚至超过真值处的情况，从而导致估值错误。由于本文对参数联合估计的方法建立在对载波频偏fe的估计的前提下，且对于多径衰落信道环境，fe估值准确度会直接影响后续参数θ和ε估值的准确度，因此必须要采用较高精度循环频率的检测方法。考虑到Dandawate提出的渐进最优χ2检验，即以计算信号循环协方差构造统计量，通过使用渐进最优的χ2分布情况设定判决门限从而最终确定信号实际循环频率，简称CT算法[7]。其具体步骤如下。

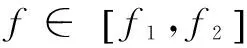
(15)

(16)

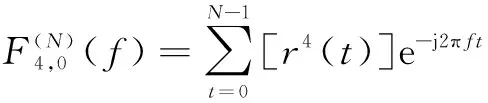
(17)

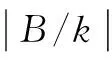
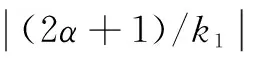
(18)

2.2.2 初始相位估计

由式(9，11)可知，当取循环频率α=4fe，即β=0时，每一路径信号的循环累积量cri(α,0)4,0与定时误差ε无关，其相位包含了初始相位信息，即

(19)

由式(10)可得多径信道下信号循环累积量为

(20)

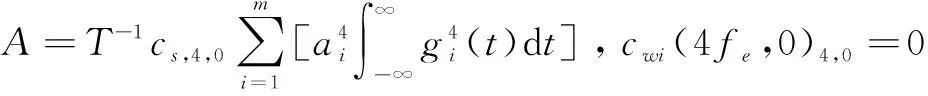
(21)

2.2.3 定时误差估计

为使定时误差信息包含在循环累积量中，令式(9)中β=1，即循环频率α=T-1得到

(22)

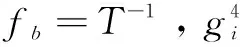
(23)

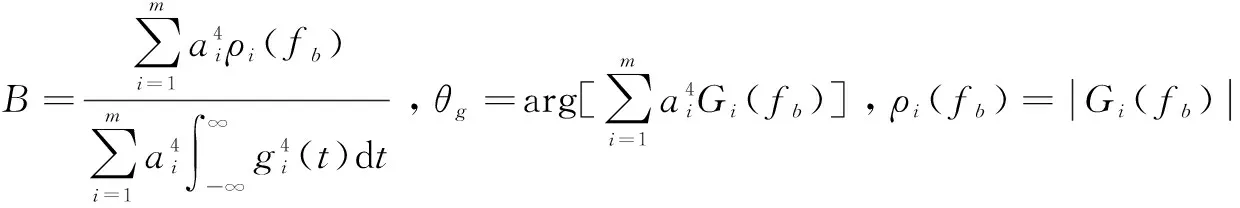
(24)

(25)

3 仿真实验与结果分析

由于本文算法研究衰落信道下线性调制信号的同步参数盲估计问题，本节仿真以不同阶数的QAM信号和QPSK信号为例，采用协议[12]中的良好、中度、恶劣短波信道和高斯白噪信道进行仿真和对比实验。未加说明的情况下，采用64QAM信号，符号数为1 000，符号速率2 400波特，采样率19 200Hz，以平方根升余弦成形滤波器作为发送和接收滤波器，滚降系数为0.5。归一化频率偏移为feT=0.1，定时误差为ε=0.375，初始相位为θ=16/π，MonteCarlo实验次数为500，精估计最小频率间隔和归一化频偏粗估计分别为k1=1×10-5,k=1×10-3，精估计搜索范围α=10k。归一化频偏和归一化最小频率间隔分别定义为fd=fe·T，kd=k·T，T为符号周期。

3.1 信道特性分析(实验1)

为了考察本文算法在多径频率选择性衰落信道下的有效性，本文选用的3种不同质量的两径短波信道参数分别为：良好短波信道，多普勒扩展[0，0.1]、信道幅度增益[1,0.5]、延迟0.000 5 ms；中度短波信道，多普勒扩展[0,0.5]、信道幅度增益[1,0.5]、延迟0.001 ms；恶劣短波信道，多普勒扩展[0,1]、信道幅度增益[1,1.5]、延迟0.002 ms。图1为信号分别通过高斯白噪、良好短波、中度短波、恶劣短波信道后的频谱幅度，信噪比均设为10 dB。由图可看出，3种短波信道对信号的频谱具有不同程度选择性衰落，其中中度和恶劣短波信道对信号频谱频率选择性衰落表现较为显著。

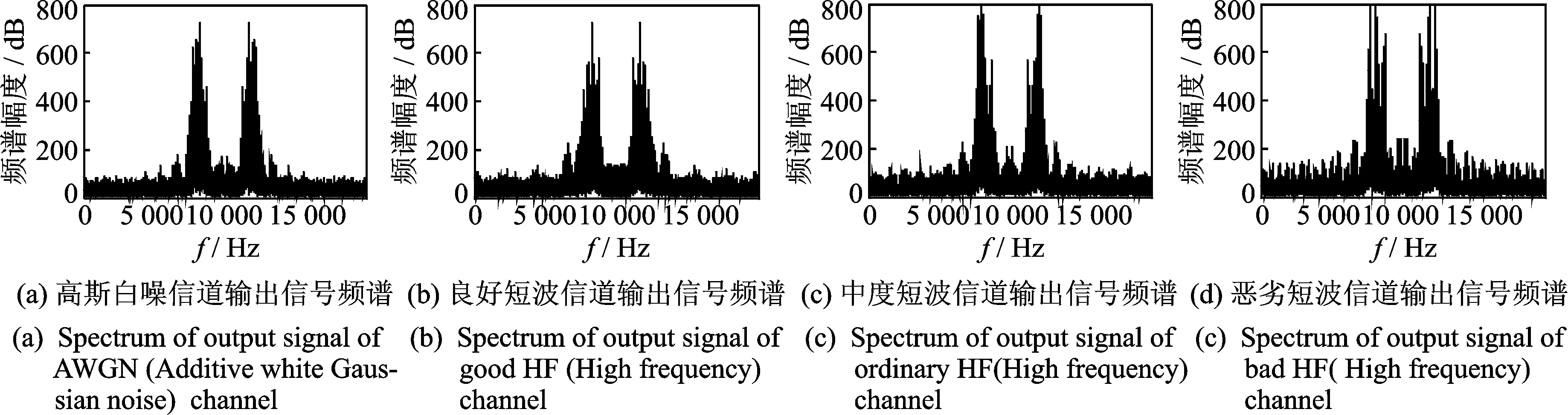
图1 衰落信道输出信号频谱Fig.1 Output signal spectrums of different channels

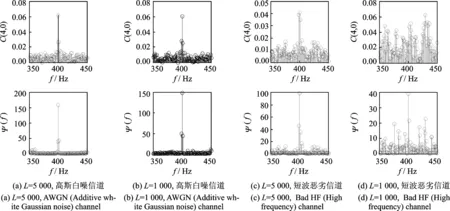
图2 循环频率检测Fig.2 Tests of cycte frequency

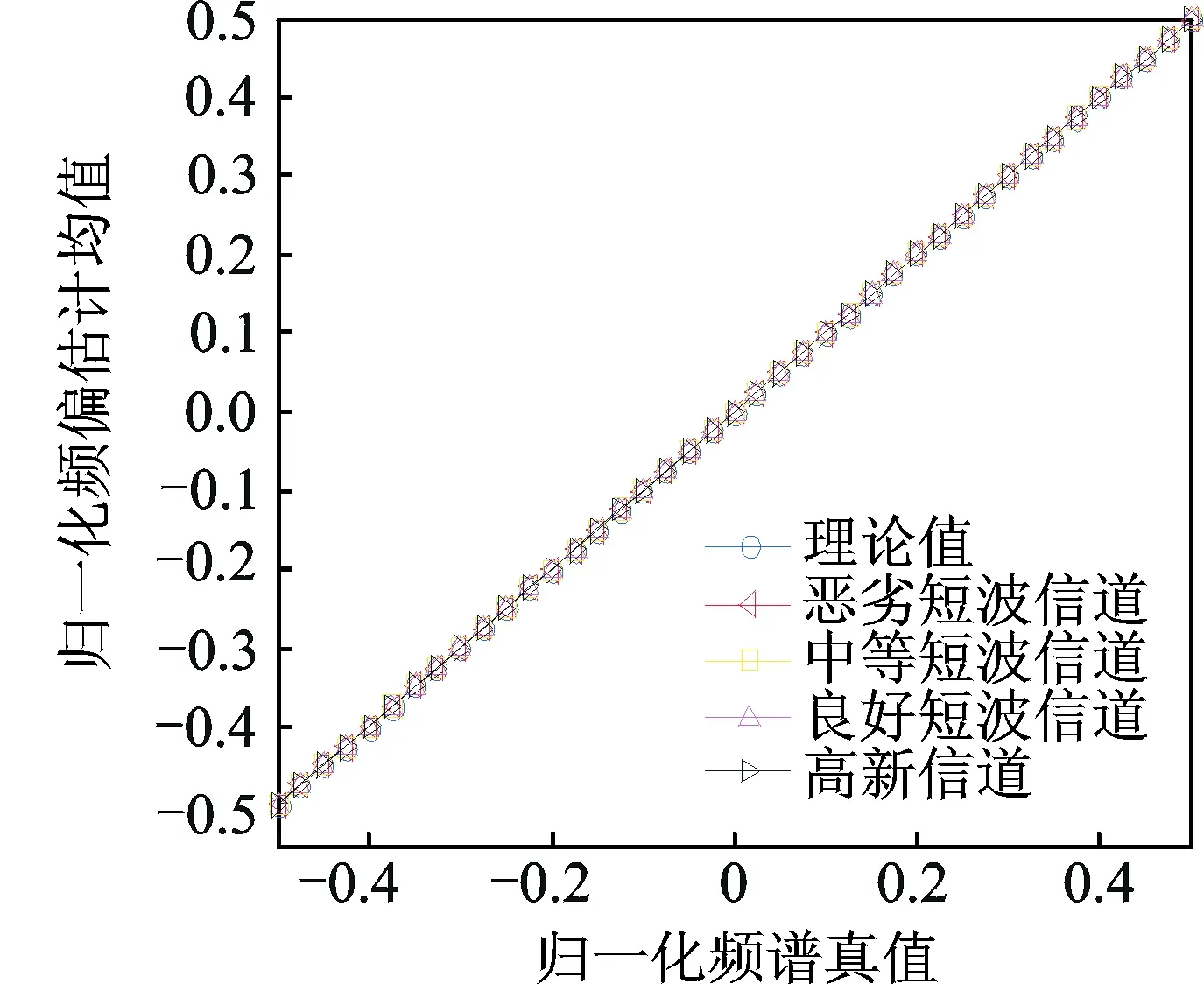
图3 归一化频偏估计均值Fig.3 Mean of normalized frequency offsets estimation

3．2 频偏估计(实验2)

由于本文联合估计算法建立在频偏估计的基础上，先考察衰落信道下CT算法在循环频率检测上较峰值检测方法的优越性。由2.2.1节知，因可用数据有限和信道、信号自噪声等因素影响，循环累积量并非只在循环频率处不为0。高斯信道和短波恶劣信道条件下信号的循环累积量如图2所示，频偏设为400 Hz，所用符号个数分别为1 000和5 000，为便于清晰观察，限定频率范围在350～450 Hz内，最小频率间隔设为1 Hz。由图可得，在高斯信道下仅依据循环累积量峰值进行循环频率检测的方法性能良好，而在恶劣短波信道下则需更多数据量才能较为明显地体现循环统计量特征。在面对恶劣短波信道时，CT算法能够较好地克服信道影响，峰值较为明显，且检测循环频率所需符号少，更有利于在恶劣信道下实现快速盲频偏估计。

为了确定频偏估计范围，设置归一化频偏的变化区间为[-0.5,0.5]，图3为信噪比为15dB时，在4种不同信道条件下不同频偏设置值对应的理论值曲线和估计均值。由图可看出，采用循环频率检测方法估计频偏有很好的估计范围，其原因在于由式(10,11)估计频偏利用的是过采样线性调制信号本身的循环平稳性，且循环频率检测无须取幅角等操作，即便在多径衰落信道下依然具有很好的稳定性。

为了考察本文算法在提高循环频率检测精度上的效果，将频偏设为100.876，以QPSK信号进行仿真，计算频偏估计均方误差，结果如图4所示。设置文献[7]算法中最小频率间隔为2.4Hz。由图4可以看出，在高斯信道和短波信道环境下，本文采用方法较文献[7]方法性能均有所提高。文献[7]算法因遍历时的最小频率间隔较大，精度偏低，导致了均方误差较大，当信噪比高于3dB时，即使继续增加信噪比，因受频偏估计精度的限制，均方误差已经没有明显降低的趋势。本文算法由于频偏估计精度的提高，随着信噪比增加，均方误差持续降低，为初始相偏和定时误差的估计打下基础。

图5为不同信噪比条件下，不同调制阶数的QPSK信号和QAM信号分别在恶劣短波信道和高斯信道条件下的频偏估计均方误差曲线。由图可看出，随着信号的调制阶数增高，频偏估计性能降低。这是由于调制阶数增大，信号自噪声随之增大，从而降低了循环累积量估计值准确度和频偏估计性能。另外，算法对信道的鲁棒性较强，印证了本文在不同信道环境下对循环频率检测的仿真分析。

3.3 初始相偏估计(实验3)

图6为分别在高斯信道、良好短波信道、中度短波信道以及恶劣短波信道条件下，64QAM信号初始相位偏转估计伴随信噪比变化的曲线。可见，在低信噪比下，相比于文献[8]算法的性能总压严重情况，本文算法显示出了较明显的优势。而在恶劣短波信道下，本文算法的相偏估计性能有所下降。这是因恶劣短波信道下的多普勒效应更为严重，使估计相偏的循环累积量值和真实值之间的差距增大，从而降低了估计值准确度。本文算法在中度短波信道和信噪比为0dB的条件下均方误差仍低于10-2，满足了实际需求。图7为不同信道下初始相位偏转的估计范围，信噪比设为0dB。由此可见，相位偏转估计范

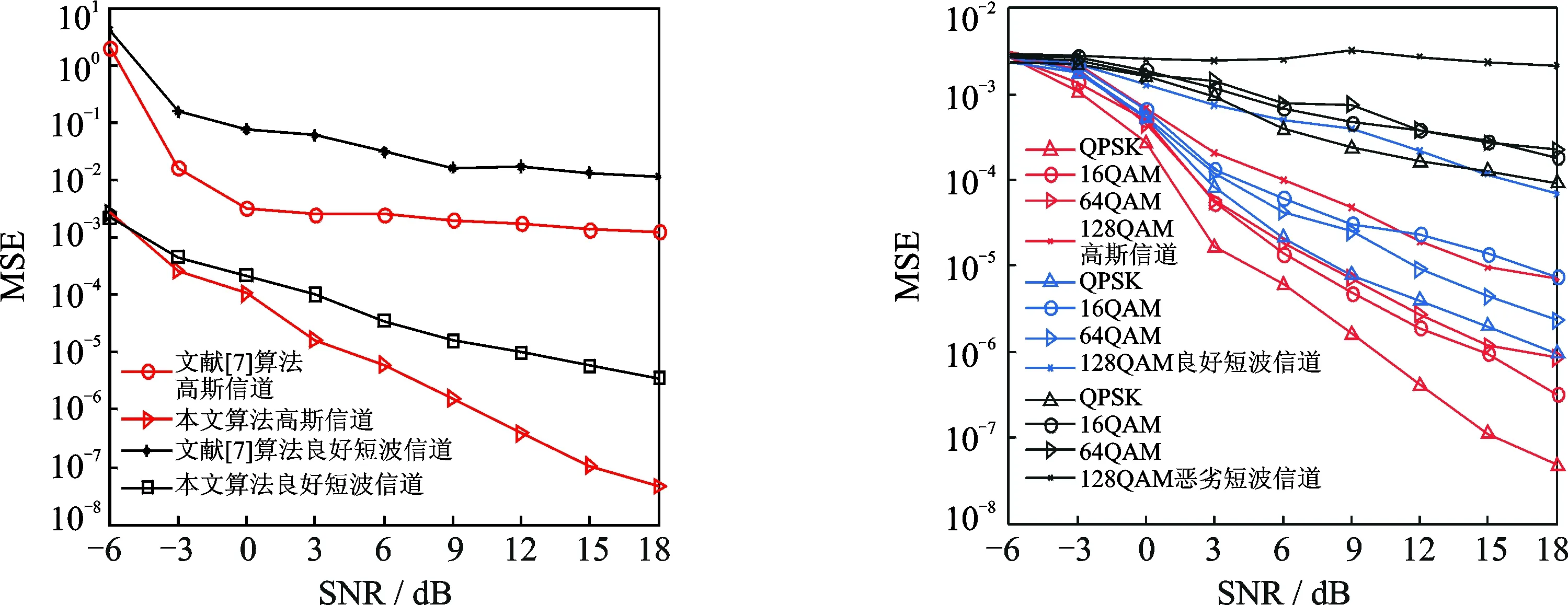
图4 改进算法频偏估计均方误差曲线

Fig.4MSEcurvesoffrequencyoffsetestimationsofthemodifiedalgorithm

图5 频偏估计均方误差随信噪比变化曲线

Fig.5MSEcurvesoffrequencyoffsetestimationsindifferentSNRs

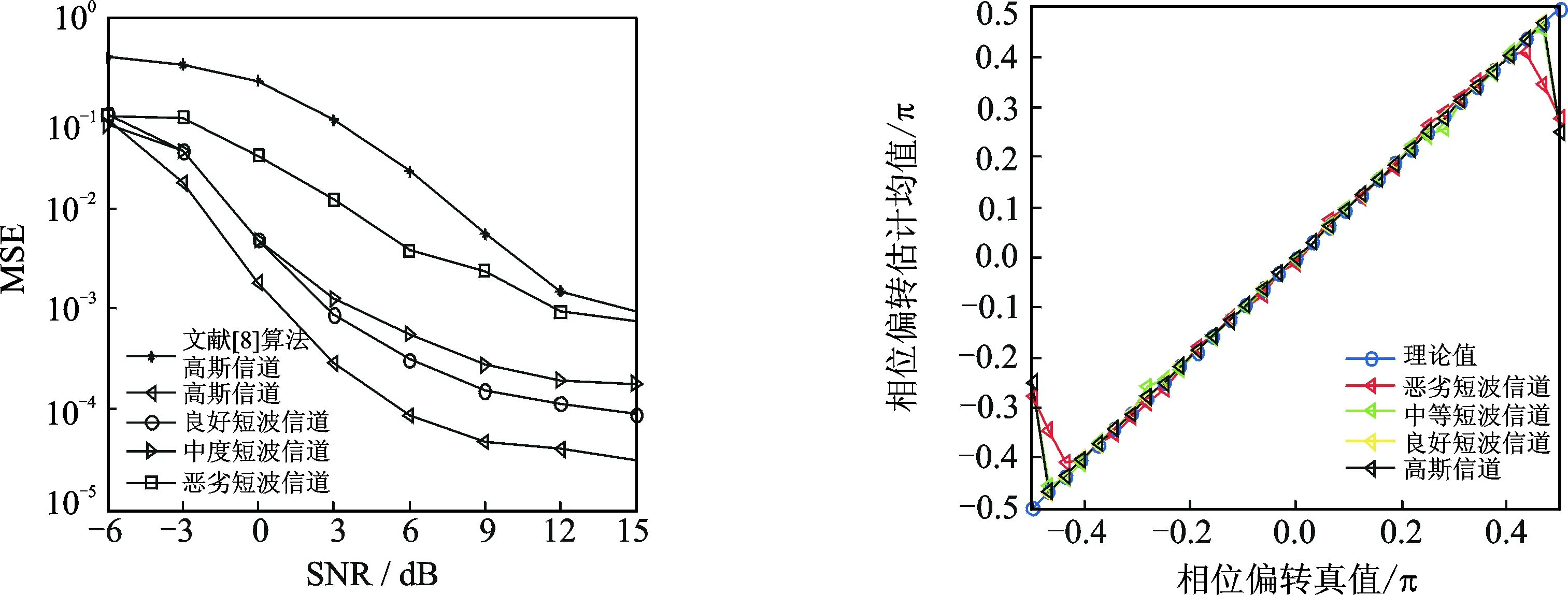
图6 初始相偏估计均方误差随信噪比变化曲线

3.4 定时误差估计(实验4)

图8为不同信道下定时误差估计均方误差曲线。因利用循环统计量的低信噪比和良好抗信道衰落特性，本文算法相较文献[5]中的算法，估计性能有了较大提高。与相位估计相比，信道和信噪比对本文算法的定时误差估计影响较小，在良好短波信道和中度短波信道下的估计性能非常接近。因信号的循环累积量估计值准确度在恶劣短波信道下降低，导致定时误差估计准确度随之降低。而在信噪比高于3dB时，各类信道下定时误差估计的均方误差值均低于10-2，可见本文算法可在低信噪比和多径衰落信道环境下更为有效地估计定时误差。

图 9为各信道下定时误差估计均值曲线，用以评估不同条件下定时误差估计范围。由图可看出，相比相偏估计，信道对定时误差的估计范围影响较大。这是因为式(25)在估计定时误差时，由于多径信道各路径间的时延形成了成形滤波，其在4倍频偏处的相频响应被忽略。而随着信道质量变差，多径间的时延增大，对定时误差估计的影响不断增大，从而导致准确估计定时误差范围不断减小。

4 结束语

本文根据循环平稳理论提出了一种针对多径衰落及较低信噪比条件下线性调制信号的频率偏移、

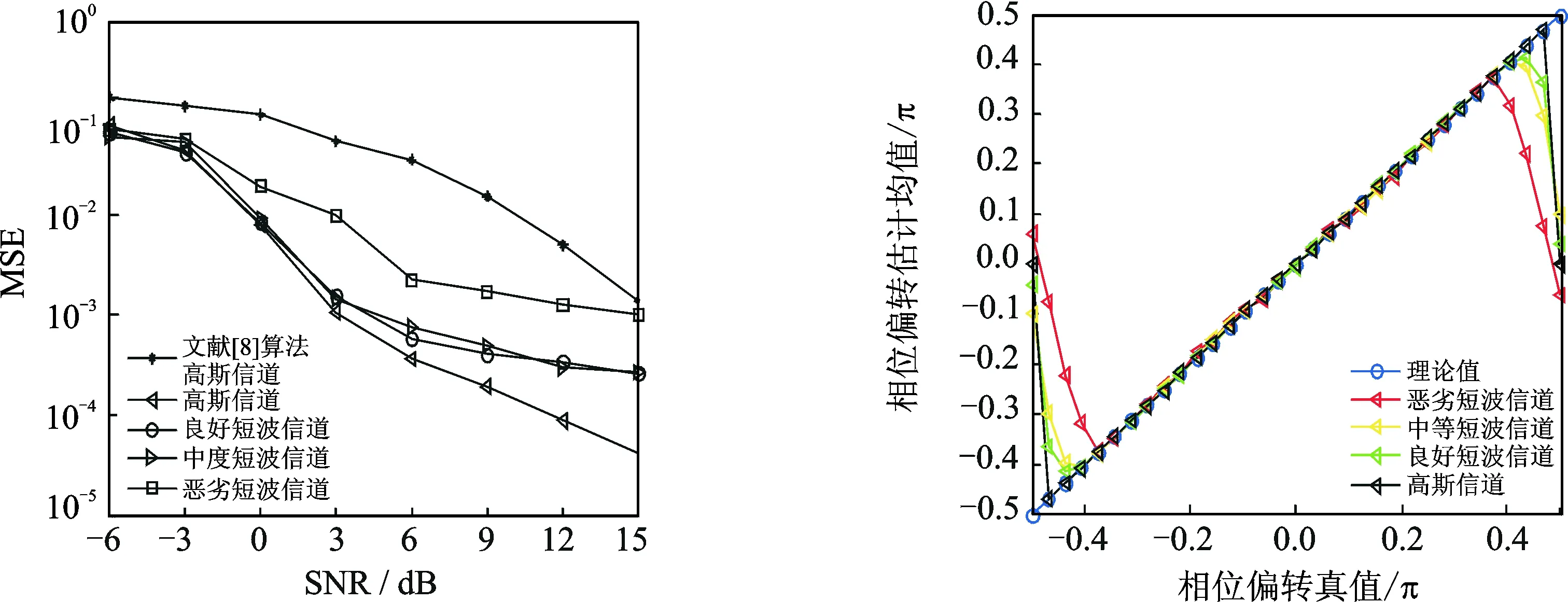
图8 定时误差估计均方误差随信噪比变化曲线

初始相偏和符号定时误差联合估计方法。利用循环累积量性质建立了多径信道下信号四阶循环累积量数学模型，在存在相偏和定时误差的情况下首先利用循环频率检测理论分粗、精两步估计出频偏，在此基础上通过特定循环频率上的循环累积量及它们之间的数学关系推导出初始相位和符号定时误差的估计表达式，从而实现参数的联合盲估计。此方法对先验知识要求少，无需调制、信噪比估计等预处理，在低信噪比多径衰落信道下能有效实现参数的联合盲估计，且估计范围大，不依赖于加性噪声和信道衰落的分布特性，优化了对各类参数分别进行估计的繁琐步骤，对信号调制方式和调制阶数鲁棒性强。

[1]GiniF,GiannakisGB.Frequencyoffsetandsymboltimingrecoveryinflat-fadingchannels:Acyclostationaryapproach[J].IEEETransactionsonCommunication, 1998, 46(3): 400-411.

[2]PanayirciE,Bar-NessEY.Anewapproachforevaluatingtheperformanceofasymboltimingrecoverysystememployingageneraltypeofnonlinearity[J].IEEETransactionsonCommunication, 1996, 44(1):29-33.

[3]ZhuWP,YanY，AhmadMO,etal.Feedforwardsymboltimingrecoverytechniqueusingtwosamplespersymbol[J].IEEETransactionsonCircuitsandSystems, 2005, 52(11): 2490-2500.

[4]ScottKE,OlaszEB.Simultaneousclockphaseandfrequencyoffsetestimation[J].IEEETransactionsonCommunication, 2006, 44(1):2263-2270.

[5]WangYan,SerpedinE,CiblatP.Blindfeedforwardcyclostationarity-basedtimingestimationforlinearmodulations[J].IEEETransactionsonWirelessCommunications, 2004, 3(3):709-715.

[6]PunchihewaA,ZhangQ,DobreOA,etal.OnthecyclostationarityofOFDMandsinglecarrierlinearlydigitallymodulatedsignalsintimedispersivechannels:Theoreticaldevelopmentsandapplication[J].IEEETransonWirelessCom, 2010, 9(8): 2588-2599.

[7]DandawateAV,GiannakisGB.Statisticaltestsforpresenceofcyclostationarity[J].IEEETransonSignalProcessing, 1994, 42(9): 2344-2369.

[8]McKilliamR,PollokA,CowleyB.Noncoherentleastsquaresestimatorsofcarrierphaseandamplitude[J].IEEE,2013, 6(13): 4888-4892.

[9]JoseR,HariK.JointestimationofsynchronizationimpairmentsinMIMO-OFDMsystem[C]∥ProcoftheInternationalConferenceonCommunications,CircuitsandSystems, 2012: 1-5.

[10]ZhangQ,DobreO.A,RajanS,etal.CyclostationarityapproachtojointblindestimationofCP-SCLDblocktransmissionparametersforcognitiveradio[C]∥IEEEICC2010.CapeTown,SouthAfrica:[s.n.],15-18.

[11]LiuR.Blindsignalprocessing:Anintroduction[J].Proc2006IntlSympCircuitsandSystems, 2006,1(2):81-83.

Blind Estimation Algorithm of Synchronization Parameters in Frequency-Selective Fading Channels

Wu Tianlin， Peng Hua， Huang Yanyan

(Institute of Information Engineering, PLA Information Engineering University, Zhengzhou, 450002, China)

To realize blind estimation of synchronization parameters of linearly digitally modulated signals in multipath fading channels and low signal-to-noise ratio (SNR), a joint algorithm for the estimation of carrier frequency offset, phase offset and symbol timing error based on cyclic cumulation is proposed. The mathematical relationships of cyclic cumulation and phase offset, symbol timing error are obtained through theoretical derivation. Based on this, the carrier frequency offset is roughly estimated firstly, then the quite precise estimation is obtained from the test of certain cycle frequency. Flinally, the phase offset and symbol timing error are estimated from the value of some certain cyclic cumulation. The algorithm do not rely on the color and distribution characteristics of the fading distortion or additive noise and is quite appropriate for complex condition that frequency offset, phase offset, time error and fading exist at the same time. Experimental results demonstrate the good performance of blind estimation of synchronization parameters in frequency selective fading channels under low SNR.

multipath frequency-selective fading; low signal-to-noise ratio (SNR); synchronization parameters; blind estimation; cyclic cumulation

2013-12-12；

2016-09-22

TN911.7

A

吴天琳(1989-)，女，硕士研究生，研究方向：信号与信息处理、短波信号处理，E-mail:wtlwtl890215@126.com。

彭华(1973-)，男，教授、博士生导师，研究方向：通信信号处理、软件无线电。

黄艳艳(1986-)，女，博士研究生，研究方向：信号与信息处理、载波同步技术研究。